Antonio García Casco

[CV] · [Petrogénesis metamórfica] · [Cristalquímica básica] · [Advanced Petrology · IPGP] · [IUGS_SCMR] · [Geotermobarometría] · [Curso: Metamorfismo como herramienta geodinámica] · [Análisis de Sistemas Heterogéneos] · [CSpace] · [Imágenes de RX] · [Prop Fisicoquímicas de los Magmas] · [Tutor de Petrología] · [Trabajo de Campo de Petrología] · [Glosario de Geología (RAC)] · [Restauración de Monumentos] · [Minerales y Rocas] · [Las rocas hacen ciudad, Granada] · [Grupo de Petrología Geoquim y Geocron (SGE)] · [Research Group RMN302] · [IGCP 546 Caribbean Subduction] · [Biblioteca Digital Cubana de Geociencias] · [Enlaces de interés] · [Notas de Prensa]

Geotermobarometría: · Calibrados

[Introducción] [Fundamentos Termodinámicos] [Bases Conceptuales] [Aplicaciones y Limitaciones] [Referencias]

[· Simplificaciones] [· Calibrados] [· Soluciones P-T simultáneas] [· Precisión y Exactitud] [· Método del Multiequilibrio] [· Cálculo de Trayectorias P-T]

Una calibración implica obtener los incrementos de las propiedades termodinámicas de la reacción entre las fases puras que permiten reproducir la dependencia P-T-X de la constante de equilibrio observada en sistemas experimentales y/o naturales. Por lo general, los calibrados presentan restricciones de aplicabilidad resultantes de los rangos P-T-X bajo los que se han analizado experimental o empíricamente los sistemas. Un elemental sentido de precaución sugiere calificar con reservas los resultados obtenidos a partir de extrapolaciones de los calibrados, ya que la linearidad de la ecuación (49) es una simplificación aplicable a rangos P-T-X determinados.

Para ejemplificar los métodos de calibrado y evaluar la significación de las constantes que aparecen en las ecuaciones propuestas en la literatura y sus limitaciones de aplicabilidad, seguiremos considerando los dos ejemplos anteriormente utilizados, el equilibrio de intercambio FeMg_-1 biotita-granate (termómetro GARB) y el equilibrio de transferencia neta entre los componentes Al₂SiO₅, anortita, grosularia y SiO₂ en las fase aluminosilicato, plagioclasa, granate y cuarzo (barómetro GASP).

Termometria en Base a Equilibrios de Intercambio

Equilibrios de Intercambio

El termómetro basado en la reacción de intercambio Fe-Mg entre granate y biotita, puede expresarse mediante la reacción entre los componentes de fase almandino (alm), piropo (prp), annita (ann) y flogopita (phl) (ec. 37; ver Tabla 1 para referencias). Ambas soluciones sólidas pueden describirse mediante modelos de mezcla generales, de tipo iónico multiposicional, para los que la actividad se define como (Tema 3 del programa de Petrogénesis Metamórfica I. Aproximación Termodinámica)[1]:

a_k = Õ[(X_i·g_i)]ni     (52)

donde el producto aplica a todas las posiciones estructurales donde ocurre la mezcla, X_i y g_i son las fracciones molares y coeficientes de actividad posicionales, respectivamente, de los componentes elementales en las distintas posiciones estructurales, y n_i es la multiplicidad de estas posiciones. Si aplicamos estos modelos de solución generales a granate y biotita, las actividades de almandino y annita, por ejemplo, son:

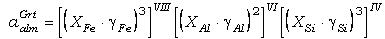     (53)

     (54)

donde la mezcla se produce en todas las posiciones estructurales, indicadadas por la coordinación en números romanos[2], excepto en las ocupadas por el oxígeno. Si se sustituyen las expresiones (53) y (54), y las expresiones equivalentes para las actividades de piropo y flogopita, en la ecuación (23) para el equilibrio de intercambio biotita-granate (ec. 37), reajustando y simplificando, obtenemos:

     (55)

En este punto, merecen destacarse dos aspectos de las reacciones de intercambio.

En primer lugar, las actividades posicionales de los componentes elementales que no están implicados directamente en la reacción de intercambio se cancelan, por lo que no aparecen en la expresión de la constante de equilibrio. Esta simplificación es una ventaja en el tratamiento de este tipo de equilibrios, que no ocurre en el caso de las reacciones de transferencia neta.

En segundo lugar, el balance estequiométrico de la reacción de intercambio condiciona el hecho de que todos los términos de K_eq están elevados a una misma potencia, que es igual a los moles de iones intercambiados (en este caso 3). Por tanto, puede recurrirse a una simplificación ulterior si consideramos un mol de ión intercambiado, esto es reescribiendo la reacción de intercambio (37):

1/3 Fe₃Al₂Si₃O₁₂ (alm) + 1/3 KMg₃AlSi₃O₁₀(OH)₂ (phl)
= 1/3 Mg₃Al₂Si₃O₁₂ (prp) + 1/3 KFe₃AlSi₃O₁₀(OH)₂ (ann)     (37b)

de manera que los exponentes, i.e., las multipliciadades de las posiciones estructurales (en este caso 3) y los coeficientes estequiométricos de los componentes moleculares (en este caso 1/3), se cancelan:

     (56)

y los términos de la constante de equilibrio aparecen con exponente 1. Esta cancelación de los exponentes en los términos de K_eq afecta a cualquier reacción de intercambio, incluso en el caso de que las multiplicidades de las posiciones estructurales y los coeficientes estequiométricos de los componentes moleculares sean distintos en las dos fases, como por ejemplo en el caso del intercambio Fe-Mg entre granate y clinopiroxeno (diópsido-hedenbergita; ver Tabla 1):

1/3 Fe₃Al₂Si₃O₁₂ (alm) + CaMgSi₂O₆ (di) =
= 1/3 Mg₃Al₂Si₃O₁₂ (prp) + CaFeSi₂O₆ (hd)     (57)

Constante de Equilibrio y Coeficiente de Reparto

La simplificación de K_eq realizada anteriormente es conveniente desde el punto de vista del tratamiento analítico de los equilibrios[3], ya que permite identificar la parte ideal de la constante de equilibrio con el coeficiente de distribución o reparto K_D de dos componentes entre dos fases. Para el intercambio Fe-Mg entre biotita y granate, y teniendo en cuenta que X_k = n_k/Sn_k, la ecuación (56) queda:

     (58)

donde K_g es el producto de los coeficientes de actividad posicionales.

Nótese que si la reacción de intercambio se define como en (37), con tres moles de ión intercambiado, entonces la relación entre la constante de equilibrio y el coeficiente de reparto es K_eq=K_D³. Las propiedades termodinámicas de granate y biotita son tales que el granate fracciona preferentemente el Fe respecto de la biotita. En consecuencia, los valores de K_D serán siempre menores de 1 si la reacción de intercambio se escribe como en (37), ya que (Mg/Fe)^Grt<(Mg/Fe)^Bt (o X_Mg^Grt<X_Mg^Bt). Sin embargo, debe notarse que si la reacción de intercambio se escribe en sentido contrario que en la ecuación (37), los valores de K_D serán mayores de 1, i.e., iguales al inverso del K_D para la reacción escrita como en (37)[4]. El incremento de energía libre de la reacción entre los componentes puros (DG_r^o(P,T)) presentará en cualquier caso el mismo valor absoluto, pero el signo variará en función de cómo se escriba la reacción.

En la expresión (58), el coeficiente de reparto K_D se ha expresado de formas distintas, llegándose a la formulación más simple como una razón de las razones Mg/Fe de cada fase. No obstante, esta formulación no es siempre posible. En el caso anterior puede llegarse a ella porque los elementos Fe y Mg se encuentra en una única posición estructural en las fases biotita (posición octaédrica) y granate (posición cúbica distorsionada). Sin embargo, cuando esto no es así la identificación de la parte ideal de K_eq con K_D no es posible. Este punto puede clarificarse considerando la reacción de intercambio Fe-Mg entre granate y clionopiroxeno (57). La fórmula unidad ideal del clinopiroxeno es Ca^[M2](Fe,Mg)^[M1]Si₂O₆, de manera que Ca y (Fe,Mg) están restrigidos a dos posiciones estructurales no equivalentes (M1 y M2). Siguiendo la argumentación anterior tenemos:

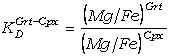     (59)

Sin embargo, los piroxenos naturales son, generalmente, deficitarios en Ca, y la posición M2 está parcialmente ocupada por (Fe,Mg), por lo que Fe^[M1] ¹ Fe_total y Mg^[M1] ¹ Mg_total, y por lo tanto K_eq ¹ K_D:

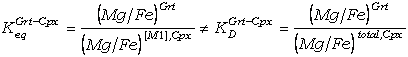     (60)

Es interesante considerar aquí la fraccionación entre dos fases de un componente diluido (e.g., traza) que sigue la ley de Henry. Este comentario se introduce por la posible utilidad en termobarometría de equilibrios entre soluciones diluidas, que a priori presentan menos problemas teóricos al poder ser considerados los coeficientes de actividad de los componentes diluidos como constantes (ley de Henry). La denominada ley de distribución de Nernst para la fraccionación de un componente diluido puede ser derivada como un caso especial de la expresión de K_D. Así, en el caso de soluciones binarias que intercambian dos componentes 1 y 2, el coeficiente de reparto puede escribirse como:

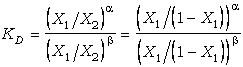     (61)

Si uno de los componentes intercambiados (e.g., el componente 1) está diluido en las dos fases, entonces (1¾X₁) » 1 y K_D » X₁^a/X₁^b. Por otro lado, si se obedece la ley de Henry, g₁=constante, y g₂=1, por lo que, para condiciones P-T fijas:

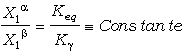     (61)

que es la ley de distribución de Nernst. Dado que K_g no varía con la composición, la partición de elementos en traza ofrece claras ventajas respecto de la partición de elementos mayores, cuyo comportamiento es generalmente no ideal, por lo que existen dificultades para definir las dependencias P-T-X de sus coeficientes de actividad. Sin embargo, hay que notar que en el caso de soluciones multicomponentes, g₁ puede no ser constante bajo concentraciones diluidas si varían las proporciones de otros componentes. El efecto de las variaciones composicionales del solvente sobre el coeficiente de actividad, y sobre la fracionación, de un componente traza será pronunciada si los componentes del solvente se comportan de forma no ideal (i.e., no siguen la ley de Raoult). Por tanto, la ley de distribución de Nerst, y su posible aplicación en termobarometría, es sólamente válida para soluciones binarias, o para soluciones multicomponentes que se comporten como binarias, esto es, aquellas en las que las porporciones de los componentes del solvente se mantengan fijas.

Fraccionación Elemental entre Granate y Biotita

La fraccionación elemental entre dos fases puede evaluarse gráficamente considerando la expresión del coeficiente de reparto como la razón de razones elementales en las dos fases (i.e., como en las ecuaciones 58 y 59). Para el intercambio Fe-Mg entre granate y biotita, obtenenos a partir de (58):

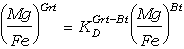     (62)

Esta relación representa una recta en el espacio (Mg/Fe)^Grt-(Mg/Fe)^Bt, cuya pendiente es igual a K_D y su intersección en el origen es = 0 (Figura 6a). Por tanto, la proyección en un diagrama (Mg/Fe)^Grt-(Mg/Fe)^Bt de rocas equilibradas a la misma presión y temperatura definirá una recta si las fases se comportan como soluciones sólidas ideales, y la proyección de rocas equilibradas a distinta temperatura o presiones definirá distintas rectas. Relaciones lineales a P y T constantes también se obtienen en diagramas ln(Mg/Fe)^Grt-ln(Mg/Fe)^Bt (Figura 6b). En estos diagramas, la intersección para valores de la abcisa = 0 (i.e., (Mg/Fe)^Bt=1) corresponden a los valores de lnK_D, como puede apreciarse tomando logaritmos naturales en (62):

     (63)

Como hemos visto más arriba, la partición de elementos entre dos fases es fuertemente dependiente de T, y en menor medida de P. Como regla general, la partición decrece a medida que T aumenta, de manera que el coeficiente de reparto K_D (y K_eq) tiende a 1, y lnK_D tiende a 0. Esto se debe a que la distinción energética entre los dos elementos decrece con la temperatura, y las dos fases tienden a presentar razones elementales más próximas (en el límite T=¥, la razón elemental de las fases es idéntica e igual a la del sistema). En consecuencia, la pendiente de las rectas en un diagrama (Mg/Fe)^Grt-(Mg/Fe)^Bt tiende a 1 a medida que la temperatura de equilibramiento aumenta. En la Figura 6a y b se han representado varias rectas correspondientes a distintos valores de K_D, menores de 1 para el caso en que la reacción de intercambio se escriba como en (37), y mayores de 1 para el caso en que se escriba en sentido contrario.

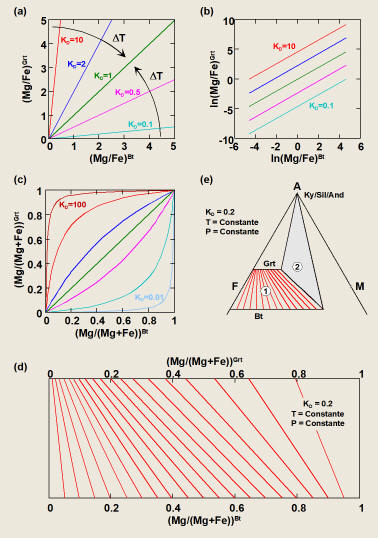
Figura 6. Distintas formas de representar la fraccionación elemental entre dos fases, ilustrada por el intercambio Fe-Mg entre granate y biotita.(a) y (b) Diagramas (Mg/Fe)^Grt-(Mg/Fe)^Bt y ln(Mg/Fe)^Grt-ln(Mg/Fe)^Bt para valores distintos de K_D (i.e., a P y/o T variables). (c) Diagrama de Roozeboom X_Mg^Grt-X_Mg^Bt para soluciones binarias Fe-Mg. (d) y (e) Diagrama de intercambio recíproco y proyección AFM para condiciones P-T constantes bajo las cuales K_D es constante. Nótese que los valores de K_D > 1 en las figuras (a), (b) y (c) corresponden a la reacción de intercambio escrita en sentido contrario a la ecuación (37).

Los diagramas representados en la Figura 6a y b son de aplicación general ya que resultan de la definición general de K_D. Para el caso más restrictivo de soluciones binarias, la definición de K_D puede reescribirse a partir de la ecuación (58), teniendo en cuenta que X_Fe^a = 1-X_Mg^a:

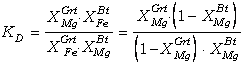     (64)

Reordenando, obtenemos:

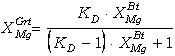     (65)

La representación gráfica de la expresión (65) en un diagrama X_Mg^Grt-X_Mg^Bt (X_Mg=Mg/(Fe+Mg)) resulta en curvas cóncavas hacia arriba para K_D<1 y cóncavas hacia abajo para K_D>1, ambas simétricas respecto de la diagonal ortogonal a la línea correspondiente a K_D=1 (Figura 6c). Estas curvas son las encontradas en el caso de partición entre soluciones ideales (i.e., K_g=1). Si una o las dos soluciones son no ideales, las relaciones de equilibrio de intercambio también vendrán definidas por curvas, pero serán asimétricas respecto de la diagonal anteriormente mencionada debido a que K_D no es constante a P y T fijas, sino que depende de la razón Mg/Fe de las fases (i.e., de roca). Esto se debe a que K_g depende de la composición (i.e., razón Mg/Fe) a P y T fijas cuando las soluciones son no ideales, por lo que K_D debe variar proporcionalmente a K_g para mantener K_eq (= K_D·K_g) constante P y T fijas.

Las relaciones anteriores para mezclas binarias pueden representarse también en diagramas de intercambio recíproco y en proyecciones de fases apropiadas como la proyección AFM, (Figuras 6d y e, respectivamente). Ambos tipos de diagramas son similares, ya que representan la composición de fases coexistentes a P y T fijas mediante líneas de compatibilidad. Sin embargo, en el primero de ellos no existen limitaciones composicionales a la coexistencia de las dos fases (i.e., las líneas de compatibilidad se distribuyen por todo el especto Mg/(Fe+Mg)^roca). Por el contrario, en los diagramas de fases de tipo AFM la composición de las fases depende de las asociaciones de fases estables para distintas composiciones de las rocas a P y T fijas. Así, rocas cuyas composiciones se proyecten en el campo difásico Grt-Bt (campo 1 en la Figura 6e) presentarán composiciones de granate y biotita variables en función de la composición de la roca, mientras que rocas cuyas composiciones se proyecten en el campo trifásico Grt-Bt-Als (campo 2 en la Figura 6e) presentarán composiciones de granate y biotita fijas, independientemente de la composición de la roca (resultado de la regla de las fases). Por otra parte, la proyección de fases coexistentes en rocas coincidirá con las relaciones de partición descritas por la ecuaciones (64)  y (65) e ilustradas en las Figuras 6d y 6e si las soluciones son binarias e ideales. En caso de soluciones no ideales, la distribución de las líneas de compatibilidad será igualmente en forma de abanico, aunque K_D no será constante a P y T fijas, sino que variará con la composición del sistema por las mismas razones que han sido expuestas anteriormente.

Para el caso más general de soluciones multicomponentes, K_D no puede ser definida como en la ecuación (64) al ser una función de variables composicionales adicionales (e.g., X_Ca^Grt; X_Al^[VI],Bt, además de X_Mg^Grt y X_Mg^Bt) y por lo tanto X_Mg^Grt no queda definida de manera única para un valor dado de X_Mg^Bt como en la ecuación (65). La proyección de datos de partición entre fases de este tipo definirá también curvas en diagramas X_Mg^Grt - X_Mg^Bt, cuya asimetría dependerá de las variaciones en otros componentes y del grado de no idealidad de las soluciones. El efecto de componentes adicionales también dependerá de la naturaleza de la no idealidad de la mezcla de estos elementos. Como demostró el trabajo pionero de Kretz (1959), este efecto suele ser sistemático, esto es, K_D varia de forma sistemática con las variaciones en los componentes adicionales. Por ejemplo, la mezcla de Ca y Mn en granates ricos en Fe+Mg es no ideal, y es conocido el efecto de las variaciones de estos elementos sobre el K_D entre granate y biotita (Figura 7a): a medida que Ca+Mn aumenta K_D disminuye de forma lineal[5]. Esta dependencia lineal puede ser explicada por modelos de solución simétricos para el granate, en combinación con interacciones energéticas casi ideales entre Fe y Mg en las dos fases  (e.g. Ganguly y Saxena, 1987, p.140).

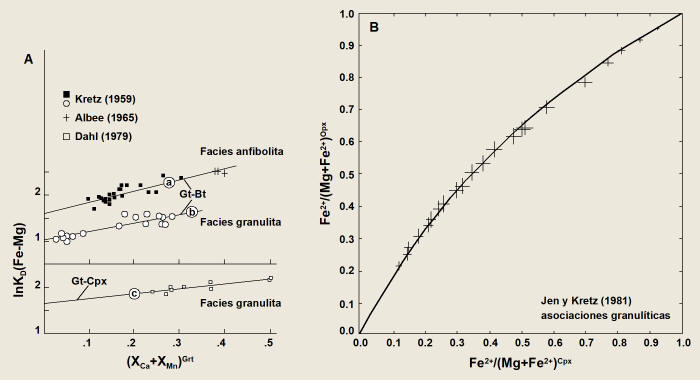
Figura 7. a) Efecto sistemático de la variación en la concentración de Ca+Mn en el granate sobre el K_D(Fe-Mg)^Grt-Bt/Cpx en rocas de grado medio y alto; este efecto indica un comportamiento no ideal del granate (nótese que K_D = (Fe/Mg)^Grt/(Fe/Mg)^Bt/Cpx, i.e., el inverso del definido a partir de la ecuación 37). b) Distribución Fe-Mg entre clinopiroxeno y ortopiroxeno de asociaciones granulíticas (Jen y Kretz, 1981); el buen ajuste de los datos a la curva sugiere que las rocas se equilibraron bajo condiciones P-T similares. Figuras reproducidas de Ganguly y Saxena (1987).

La evaluación de las irregularidades en la distribución de elementos entre fases coexistentes en las rocas, respecto de las relaciones predecibles del comportamiento ideal, necesita considerar los efectos de:

·       la proyección de muestras equilibradas a distintas presiones y/o temperaturas,

·       la proyección de muestras con asociaciones de fases en desequilibrio,

·       la dispersión analítica.

El análisis de estos puntos en series de rocas puede llevarse a cabo si se dispone de modelos de solución que permitan calcular K_g, ya que en el equilibrio y a P y T fijas debe cumplirse que K_D·K_g=constante. Si un conjunto de rocas proyectadas en diagramas como los de la Figura 6 se ajustan, dentro del error analítico, a líneas o curvas que cumplen la condición K_D·K_g=constante, puede asegurarse que están equilibradas bajo rangos P-T suficientemente restringidos (Figura 7b). En general, la dispersión analítica no puede utilizarse como argumento para justificar los desajustes de las muestras a las curvas calculadas bajo la condición K_D·K_g=constante. Si estos desajustes ocurren, es necesario concluir que los modelos de mezcla utilizados no describen bien las soluciones implicadas en los equilibrios, que las muestras no están equilibradas en rangos de P-T restringidos, o que las muestras presentan asociaciones en desequilibrio.

Una evaluación cualitativa del grado en que las rocas representan el equilibrio bajo condiciones de P y T fijas puede obtenerse a partir de la observación de cruces de líneas de compatibilidad en diagramas de fases del tipo AFM (y de intercambio recíproco), o, si las soluciones sólidas que participan en los equilibrios son casi-ideales, a partir de los diagramas de las Figuras 6a, 6b y 6c.

Calibrados del Termómetro de Intercambio entre Granate y Biotita

Los calibrados experimentales del equilibrio de intercambio Fe-Mg entre biotita y granate han sido realizados por Ferry y Spear (1978) y Perchuk y Laurent’eva (1983). Aunque existen dos calibrados empíricos previos, propuestos por Thompson (1976) y Goldman y Albee (1977), es conveniente comenzar la presente exposición por los calibrados experimentales, particularizando en el realizado por Ferry y Spear (1978) ya que es el utilizado más comunmente.

Ferry y Spear (1978) llevaron a cabo experimentos de equilibramiento de mezclas de granate almandínico de composición conocida y constante (prp₁₀alm₉₀) y biotita en la proporción 49:1 en el sistema pseudobinario Fe-Mg. Las condiciones experimentales fueron isobáricas (2070 bar), a temperaturas entre 550 y 800 ºC. Debido a la elevada proporción de granate respecto de biotita, el intercambio Fe-Mg entre las dos fases durante los experimentos no modifica de forma efectiva la composición de granate, que permanece constante. Este diseño condiciona que durante los experimentos sólo varie la composición de la biotita, que en equilibrio es también rica en Fe. Así, la variación del coeficiente de reparto K_D observada en cada experimento, desde el inicio del mismo (en desequilibrio, donde K_D=K_D^deseq) hasta su final (en equilibrio aproximado, donde K_D=K_D^eq), se debe exclusivamente a las variaciones en la composición de la biotita. Los experimentos de equilibramiento a cada presión y temperatura se realizaron de forma que K_D^eq se aproximó desde los dos lados de la reacción, esto es, partiendo de composiciones iniciales de biotita contrastadas de forma que se obtuviesen valores de K_D^deseq > K_D^eq (i.e., en un lado de la reacción) y K_D^deseq < K_D^eq (en el lado opuesto).

Los resultados experimentales de Ferry y Spear (1978) se presentan en la Figura 8a en un diagrama lnK_D-1/T. Este tipo de diagrama es conveniente para representar los resultados experimentales isobáricos ya que, según las ecuaciones (35) y (41), lnK_eq es una función de 1/T a P constante. Si las soluciones sólidas son ideales (K_g=1; K_eq=K_D) en el rango P-T-X de los experimentos y se cumple que DCp_r»0 (ec. 46) y DV_r^o(P,T)ºconstante (ec. 47), entonces los resultados experimentales deben ajustarse a una línea. Como puede apreciarse en la Figura 8a, este es el procedimiento seguido por Ferry y Spear (1978), que ajustan los datos experimentales a la recta:

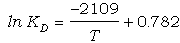     (66)[6]

Comparando la ecuación (66) con la ecuación (49), obtenemos:

DS_r^o(1,298)/3·R = 0.782     (67)

[-DH_r^o(1,298)-P·DV_r^o(1,298)] /3·R = -2109     (68)

donde T es la temperatura absoluta y el factor 3 aparece ya que la ecuación (49) está escrita en función de K_eq, y la reacción de intercambio se considera como en la ecuación (37), de manera que K_eq=K_D³. De las ecuaciones (67) y (68) pueden deducirse los incrementos de las propiedades termodinámicas de la reacción de intercambio, teniendo en cuenta que la presión de los experimentos es 2070 bar y que el incremento de volumen de la reacción entre los componentes puros es 0.238 J/(bar·mol):

DS_r^o(1,298) = 3·R·0.782 = 19.51 J/(mol·K)     (69)

DH_r^o(1,298) = 3·R·2109 - 2070·0.238 = 52112 J/mol     (70)

(R=1.9872 cal/K·mol=8.3143 J/K·mol). Sustituyendo estos valores en la ecuación (49), el calibrado de Ferry y Spear (1978) es:

0 = 52112 - 19.51·T(K) +0.238·P(bar) + 3·R·T·lnK_D     (71)

que, despejando para T, queda:

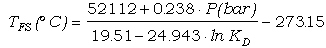     (72)

En la Figura 9 se presenta la solución gráfica de este calibrado.

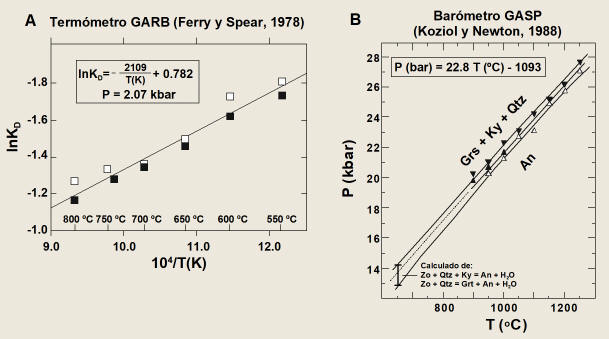
Figura 8. Calibrados experimentales a) del termómetro GARB (Ferry y Spear, 1978) y b) del barómetro GASP (Koziol y Newton, 1988).

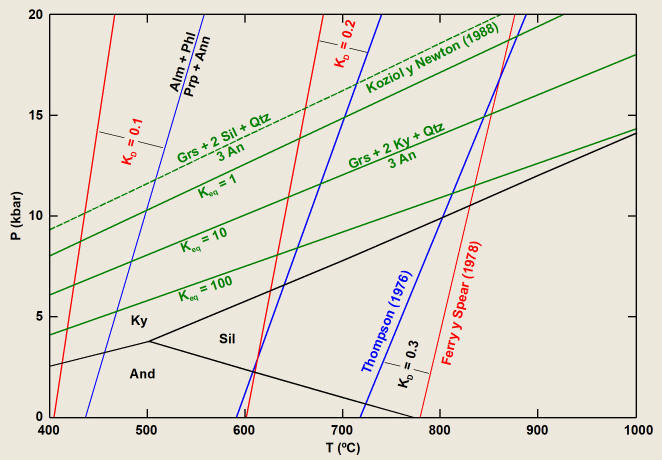
Figura 9. Soluciones de algunos calibrados del termómetro GARB (Thompson, 1976, empírico; Ferry y Spear, 1978, experimental) y barómetro GASP (Koziol y Newton, 1988; experimental). Nótese que, por comparación con la Figura 5, en este caso se ha representado K_D  en lugar de K_eq (=K_D³) para el termómetro, y que la proyección del equilibrio GASP entre las fases puras con silimanita es metaestable. Los campos de estabilidad de los polimorfos de Al₂SiO₅ según Holdaway (1971).

Puede apreciarse que las isopletas de K_D son líneas con fuerte pendiente dP/dT. La función que define las pendiente es dependiente del K_D:

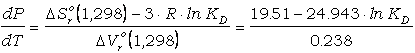     (73)

variando entre 323 bar/grado para K_D=0.1 hasta 208 bar/grado para K_D=0.3. Esto implica que el termómetro es poco sensible a la presión de equilibramiento asumida. Por otra parte, podemos apreciar la similitud de este calibrado con los resultados presentados en la Figura 5, donde la ecuación que describe el equilibrio no es lineal en P y T ya que incluye los incrementos de capacidad calorífica, de expansión térmica y de compresibilidad.

La aplicación de la ecuación (72) a rocas naturales debe ceñirse a las condiciones experimentales, i.e., entre 550 y 800 ºC, a bajas presiones y composiciones de granate y biotita dentro del sistema pseudobinario Fe-Mg y con razones (Mg/Fe)^roca bajas. Debido a la escasa dependencia de P, las extrapolaciones en la presión asumida de equilibramiento no son problemáticas. Las extrapolaciones en temperatura no son problemáticas a alta T, ya que la coexistencia de granate+biotita en sistemas ricos en Fe rara vez supera los 800 ºC. Las extrapolaciones a baja T son menos fiables ya que no queda garantizada la dependencia lineal entre lnK_D y 1/T y las soluciones Fe-Mg se desvían más fuertemente de la idealidad. En este sentido, parece que la suposición de comportamiento ideal de las soluciones en el sistema pseudobinario Fe-Mg es apropiada para la biotita, aunque no para el granate (e.g., Ganguly y Saxena, 1984, 1987).

La extrapolación en la composición de las fases es, claramente, la fuente de errores más importantes en la estimación de la temperatura de equilibramiento. Esto es debido al comportamiento no ideal de mezclas cuaternarias Ca-Mn-Fe-Mg en el granate y Al-Ti-Fe-Mg (en las posiciones octaédricas) en la biotita. Ferry y Spear (1978) recomiendan el uso de su calibrado siempre que estos componentes adicionales se encuentre en baja proporción, en concreto X_Ca^Grt+X_Mn^Grt<0.2  y X_Al^[VI],Bt+ X_Ti^[VI],Bt<0.15.

Antes de considerar el efecto de otros componentes, conviene describir brevemente el calibrado empírico de Thompson (1976), ya que ilustra los métodos de calibración empírica más comunmente utilizados.

Thompson (1976) calibró el equilibrio de intercambio Fe-Mg entre biotita y granate a partir del conocimiento del K_D de asociaciones naturales cuyas temperaturas de equilibramiento eran conocidas o asumidas por el autor (entre 500 y 700 ºC). La ecuación termométrica se obtiene mediante un análisis de regresión lineal de lnK_D sobre 1/T, que en este caso resulta en la ecuación (r=0.976):

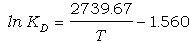     (74)

en que la reacción de intercambio se escribe en sentido contrario al de la ecuación (37). Por esta razón, los signos de las constantes n la ecuación (74) son los contrarios a los encontrados por Ferry y Spear (1978), aunque los valores absolutos son similares (cf. eq. 66).

Comparando las ecuaciones (74) y (49), y teniendo en cuenta que K_eq=K_D³, se pueden extraer los valores de las funciones termodinámicas molares mediante el procedimiento seguido para el calibrado de Ferry y Spear (1978) anteriormente discutido: DH_r(1,298)=–68334.72 J/mol, DS_r(1,298)=–38.11 J/mol·K y DV_r(1,298)=–0.5837 J/bar·mol. Debe notarse que la aproximación empírica de Thompson (1976) considera implícitamente los efectos de componentes adicionales en solución, y las correspondientes desviaciones de la idealidad de las fases, ya que las fases naturales analizadas contienen cantidades apreciables de otros componentes que sustituyen a Fe y Mg. Por esta razón, los valores extraidos para los incrementos de las propiedades termodinámicas no pueden hacerse equivalentes a los correspondientes valores de reacción entre los componentes puros. En sentido estricto, estos valores corresponden a los incrementos de las propiedades termodinámicas de reacción entre los componentes puros más los incrementos respectivos de las propiedades termodinámicas de exceso de reacción. Sustituyendo los valores anteriores en la ecuación (49), y dividiendo por 3·R para simplificar, obtenemos:

0 = -2739.646 + 1.560·T - 0.0234·P + T· lnKD     (75)

que puede solucionarse para T (P en bar):

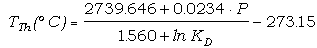     (76)

En la Figura 9 se presenta la solución gráfica de este calibrado. En este caso, las isopletas de K_D son líneas con pendiente dP/dT menores que las correspondientes al calibrado de Ferry y Spear (1978), debido a los distintos valores inferidos para los incrementos de entropía y, sobre todo, de volúmen de reacción. La pendiente dP/dT calculada a partir de:

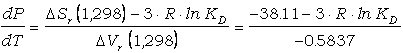     (77)

varía entre 164 bar/grado para K_D=10 (equivalente a K_D=0.1 para la reacción escrita en sentido contrario, como en la ecuación 58) hasta 117 bar/grado para K_D=3.33 (equivalente a K_D=0.3 para la reacción escrita en sentido contrario). Esto implica que este calibrado es más sensible a la presión de equilibramiento asumida que el de Ferry y Spear (1978).

En principio, podría concluirse que el calibrado de Thompson (1976) es más apropiado que el de Ferry y Spear (1978), ya que implícitamente considera el efecto de componentes adicionales y las desviaciones de la idealidad de las soluciones sólidas. No obstante, las temperaturas calculadas con este termómetro llevan asociadas una elevada incertidumbre debido a los errores en las estimaciones independientes de P y T para las asociaciones que sirvieron para su calibrado. A pesar de ello, algunos autores han señalado la validez “geológica” de este calibrado (e.g., Indares y Martignole, 1985, para rocas de alto grado).

Existen un gran número de modificaciones a los calibrados precedentes que introducen correcciones a-X (modelos de actividad) a fin de tener en cuenta las desviaciones de la idealidad de las soluciones sólidas naturales. Estas correcciones se han implementado generalmente al calibrado experimental de Ferry y Spear (1978), ya que las composiciones de las fases utilizadas corresponden al sistema pseudobinario Fe-Mg, y por lo tanto en los parámetros termodinámicos extraidos no existe término de exceso alguno correspondiente a la mezcla de otros componentes. En otras palabras, si las correcciones debidas a la mezcla no ideal de componentes adicionales son necesarias, su formulación analítica debe implementarse sobre ecuaciones que describan el sistema libre de esos componentes adicionales. Si estas correcciones se aplicasen los calibrados de Thompson (1976) o Perchuk y Laurent’eva (1983), que llevan implícitas estas correcciones, se sobrevaloraría el efecto de mezcla no ideal de otros componentes.

Todos los estudios que han analizado el intercambio Fe-Mg entre biotita y granate coinciden en la no-idealidad de ambas fases (ver Ganguly y Saxena, 1987), aunque prácticamente todos ellos se han focalizado en el problema de la solución sólida del granate, considerando que g_Fe^[VI],Bt=g_Mg^[VI],Bt=1. Para ilustrar los efectos de otros componentes, consideraremos aquí brevemente algunas de las modificaciones del calibrado de Ferry y Spear (1978) más populares.

Newton y Haselton (1981) y Hodges y Spear (1982) consideran el efecto de la desviación de la idealidad de las soluciones de granate y asumen que el comportamiento de la biotita es ideal. En este caso, podemos expresar la constante de equilibrio para el intercambio como (cf. ec. 55):

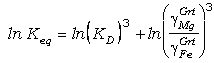     (78)

Estos autores modelizan el comportamiento no ideal del granate mediante el modelo de solución cuaternaria simétrica de Ganguly y Kennedy (1974) (o de mezcla simple, cf. Ganguly y Saxena, 1987, p.135). Este modelo considera sólo las interacciones binarias y no las multicomponentes en la expresión de la no-idealidad. Según este modelo, el incremento de energía libre de exceso de la reacción (por mol de catión intercambiado) es:

R·T·ln(g_Mg/g_Fe)^Grt = W_FeMg(X_Fe–X_Mg) + (W_MgCa–W_FeCa)·X_Ca + (W_MgMn–W_FeMn)·X_Mn     (79)

donde X_i=i/(Fe+Mg+Ca+Mn) y W_ij son los parámetros de Margules de interacción binaria simétrica i-j en el sistema cuaternario Ca-Mn-Fe-Mg. Este modelo no es aceptado actualmente debido, sobre todo, a la suposición de interacciones binarias simétricas. Newton y Haselton (1981) y Hodges y Spear (1982) consideran todos los parámetros de Margules = 0 excepto el parámetro de interacción entre Mg y Ca:

W_MgCa = 3300 – 1.5·T cal/mol de catión = 13807.2 – 6.276·T J/mol de catión     (80)

Sustituyendo (80) y (79) en (78), y sustituyendo la expresión resultante en la ecuación (55), junto con los incrementos de las propiedades termodinámicas de la reacción de intercambio extraídos del calibrado de Ferry y Spear (1978), obtenemos la corrección siguiente:

0 = 12454 - 4.662·T + 0.057·P + 3·R·T·lnKD + 3·(3300 - 1.5·T)·X_Ca^Grt     (81)

y despejando para T:

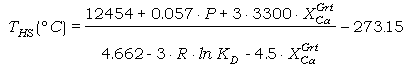     (82)

donde las constantes se han expresado en calorías en lugar de en julios ya que es la formulación común en la literatura.

Ganguly y Saxena (1984, 1985), tras un análisis de los datos termodinámicos disponibles sugieren que la mezcla en el sistema binario Fe-Mg es asimétrica, y ofrecen otros valores para los parámetros de Margules de interacción binaria:

W_MgCa–W_FeCa = DW_Ca = 3000 ± 500 cal/mol de catión     (83)

W_MgMn–W_FeMn = DW_Mn = 3000 ± 500 cal/mol de catión     (84)

W_FeMg = W_Fe-Mg· Mg/(Mg+Fe) + W_Mg-Fe·(Fe/(Mg+Fe)     (85)

W_Fe-Mg = 200 cal/mol de catión     (86)

W_Mg-Fe = 2500 ± 500 cal/mol de catión     (87)

La corrección resultante es:

0 = 12454 – 4.662·T + 0.057·P + 3·R·T·lnK_D + 3·[W_FeMg·(X_Fe^Grt–X_Mg^Grt) + DW_Ca·X_Ca + DW_Mn·X_Mn]     (88)

de la que hay que despejar para T (con alguna otra modificación, ver Ganguly y Saxena, 1984 y 1985 para más detalles). Los parámetros de mezcla, y por lo tanto la corrección del calibrado, están definidos para composiciones de X_Ca^Grt y X_Mn^Grt<0.3, y para valores de (Fe/Mg)^Grt>3; en caso contrario la suposición de mezcla asimétrica no ideal entre Fe-Mg no está  garantizada, por lo que podría obviarse el parámetro W_FeMg en la formulación termométrica (como es el caso de granates ricos en prp de grado alto).

Existen otras correcciones más recientes basadas en modelos de solución más refinados para el granate, entre los que pueden citarse los de Anovitz y Essene (1987), Geiger et al. (1987), Koziol y Newton (1989), Koziol (1990) y Berman (1990). En el caso de Berman (1990), la solución se modeliza mediante un modelo general asimétrico cuaternario, y la ecuación que define el coeficiente de actividad del componente m es un polinomio de tercer grado en la composición expresable como:

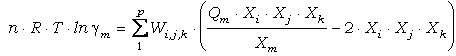     (89)

 donde cada parámetro de Margules W_i,j,k es una función de P y T: W^G_i,j,k=W^H_i,j,k-T·W^S_i,j,k+P·W^V_i,j,k (W^H, W^S y W^V se asumen constantes independientes de P, T y la composición), Q_m es un término que da cuenta del número de i, j y k que son iguales a m, y p es el número de parámetros de mezcla necesarios para una solución dada (número de permutaciones posibles entre i, j y k). Berman (1990) calculó los parámetros ternarios a partir de las interacciones binarias según el modelo de Wohl (1953):

W_i,j,k = (W_i,i,j + W_i,j,j + W_i,i,k + W_i,k,k + W_j,j,k + W_j,k,k)/2 - C_i,j,k     (90)

aunque haciendo el término ternario C_i,j,k = 0 debido a la ausencia de datos experimentales necesarios para calibrar las interacciones ternarias. La extensión de la ecuación para almandino, por ejemplo, es:

3·R·T·lng_Fe^Grt = W112(-2X12X2) + W122(-2X1X22) + W113(X12-2X12X3) + W133(2X1X3-2X1X32) +
+W114(-2X12X4) + W144(-2X1X42) + W223(X22-2X22X3) + W233(2X2X3-2X2X32) +
+W224(-2X22X4) + W244(-2X2X42) + W334(2X3X4-2X32X4) + W344(X42-2X3X42) +
+ W123(X1X2-2X1X2X3) + W124(-2X1X2X4)+
+ W134(X1X4-2X1X2X4) + W234(X2X4-2X2X3X4)       (91)

donde las X_i se refieren a las fracciones molares de 1=Ca, 2=Mg, 3=Fe, 4=Mn, y W_i,j,k como en la ecuación (89). La expresión de g_Fe^Grt (91) y la correspondiente para g_Mg^Grt deben sustituirse en la ecuación (78), y ésta última a su vez debe sustituirse en la ecuación (55), junto con los incrementos de las propiedades termodinámicas de la reacción de intercambio extraidos del calibrado de Ferry y Spear (1978) para obtener la corrección al termómetro. Nótese que en este caso, los W_i,j,k son funciones de P, T y X_i, y el despeje de T es algo más complicado que en los casos anteriores. En principio, esta corrección permite extrapolar el calibrado de Ferry y Spear a cualquier composición de granate.

De la misma manera que para el granate, se han desarrollado expresiones de los coeficientes de actividad para los componentes en solución en la biotita. Estas han sido propuestas a partir del análisis de datos naturales (Indares y Martignole, 1985; Sengupta et al., 1990; Hoisch, 1991), y experimentales (Patiño Douce et al., 1993). Como ejemplo, consideraremos aquí la corrección de Indares y Martignole (1985)

Estos autores consideran el efecto del Ti y Al^[VI] en la desviación de la idealidad de la biotita, asumiendo un modelo de solución cuaternaria simétrica Fe-Mg-Ti-Al en las posiciones octaédricas (Ganguly y Kennedy, 1974). El cálculo de DW_Al^[VI],Bt=W_Mg-Al–W_Fe-Al y DW_Ti^Bt=W_Mg-Ti–W_Fe-Ti) es empírico, realizado por análisis de regresión sobre muestras de granulitas donde existen estimaciones independientes de P y T. El método es similar al utilizado por Thompson (1976), aunque en este caso la ecuación a la que se ajusta la regresión contiene como incógnitas los parámetros anteriores (DW_Al^[VI],Bt=m, y DW_Ti^Bt=n) y como coeficientes conocidos los incrementos de las propiedades termodinámicas de la reacción entre los componentes puros y los parámetros de mezcla del granate. En base a estos últimos, desarrollan dos formulaciones distintas, siguiendo los modelos de Newton y Haselton (1981) y Hodges y Spear (1982) por una parte (modelo A), y de Ganguly y Saxena (1984) por otra (modelo B). Este último modelo es modificado por Indares y Martignole (1985), quienes sugieren que el parámetro de Margules que describe la no-idealidad de la solución Fe-Mg (i.e. W_FeMg) en el granate puede no ser válido para valores de (Fe/Mg)^Grt<3, tal y como señalan Ganguly y Saxena (1984), y para condiciones de alta T, por lo que no incluyen este parámetro en la regresión de los datos para obtener su corrección B. Las ecuaciones termométricas son (los parámetros y constantes en calorías):

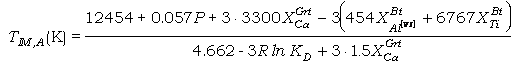     (92)

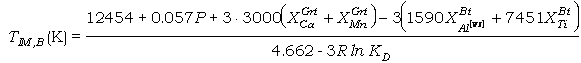     (93)

donde los parámetros DW_Al^[VI],Bt y DW_Ti^Bt obtenidos en las regresiones son los coeficientes que multiplican a X_Al^[VI],Bt y X_Ti^Bt, respectivamente, en cada ecuación.

Algunos autores han señalado los buenos resultados obtenidos con estas correcciones (e.g., Bohlen y Lindsley, 1987), aunque existen bastantes limitaciones en su aplicabilidad. En primer lugar, debe restringirse a condiciones de facies de granulitas. Por otra parte, las correcciones propuestas pueden no ser satisfactorias para describir los efectos del Al y Ti en las biotitas, ya que el rango de variación composicional de las biotitas usadas por Indares y Martignole (1985) en las regresiones es muy limitado para resultar en valores de DW_Al^[VI],Bt y DW_Ti^Bt significativos (ver Ganguly y Saxena, 1987, p 238). Así, Sengupta et al. (1990) han evaluado los parámetros (W_Mg-Al–W_Fe-Al)^Bt y (W_Mg-Ti–W_Fe-Ti)^Bt para el intercambio Fe-Mg entre ortopiroxeno y biotita en granulitas siguiendo la misma técnica que Indares y Martignole (1985), resultando en 3595 cal/mol catión y 4423 cal/mol catión, respectivamente. Estos valores contrastan con los ofrecidos por Indares y Martignole (1985), sobre todo para el caso del modelo A (ver también Hoisch, 1991 y Patiño Douce et al., 1993). Finalmente, las restricciones impuestas por las muestras naturales utilizadas en las regresiones implican que estos calibrados deben aplicarse a rocas en las que (Fe/Mg)^Grt<3 y donde el balance del Al^[VI] y Ti en la biotita se verifique mediante la sustitución Ti-vacante y di-trioctaédrica (este último aspecto es remarcado por Indares y Martignole, 1985).

A pesar de estas limitaciones, muchos autores han aplicado los calibrados de Indares y Martignole (1985) bajo condiciones P-T-X fuera del rango utilizado en los calibrados, como en rocas de grado medio donde (Fe/Mg)^Grt > 3, y sin demostrar que la solución de biotita en las posiciones octaédricas se ajusta a las premisas indicadas más arriba.

Barometría en Base a Equilibrios de Transferencia Neta: Barómetro GASP

Como se ha indicado más arriba, los equilibrios de transferencia neta sólido-sólido suelen presentar incrementos de volumen de reacción suficientes para ser utilizados como barómetros (Tabla 3). De entre ellos, el basado en el equilibrio entre granate, silicato de Al, cuarzo y plagioclasa (GASP), expresado mediante la reacción de transferencia neta entre los componentes de fase grosularia, silicato de Al, cuarzo, y anortita (ec. 36; ver Tabla 3 para referencias), ha sido uno de los mejor estudiados.

El calibrado de este equilibrio puede abordarse partiendo de la condición (23):

     (94)

donde las actividades de los componentes cuarzo y silicato de Al son a_qtz^Qtz=a_als^Ky,Sil,And=1 ya que las fases cuarzo y silicato de Al pueden considerarse puras. La aplicación práctica de este barómetro necesita, por tanto, conocer formulaciones explícitas para DG_r^o(P,T) y disponer de modelos de actividad para el granate y la plagioclasa. Abordaremos estos dos aspectos a continuación.

Calibrados del Equilibrio GASP entre las Fases Puras

El calibrado del equilibrio entre las fases puras es el primer estadio en la calibración de una reacción, ya que permiten deducir los incrementos de las propiedades termodinámicas que permite conocer DG_r^o(P,T). La reacción entre las fases puras define el límite superior de estabilidad de anortita a alta presión, y su localización en el espacio P-T tiene lugar en el campo de estabilidad de la distena (Figura 8b).

Las calibraciones experimentales de la reacción GASP entre las fases puras incluyen los trabajos de Hays (1967), Hariya y Kennedy (1968), Schmid et al. (1978), Goldsmith (1980), Gasparik (1984) y Koziol y Newton (1988). De ellos, el calibrado de Goldsmith (1980) primero, y el de Koziol y Newton (1988) después, han sido los más utilizados para realizar estimaciones de presión. A partir de los datos de Goldsmith (1980), la ecuación que describe la reacción entre las fases puras con distena es:

P^O (bar) = -2100 + 23.2·T (ºC),  con distena     (95)

De este calibrado y del calibrado experimental de la reacción Ky=Sil de Holdaway (1971), Newton y Haselton (1981) ofrecen la correspondiente ecuación para la reaccion con silimanita:

P^O (bar) = -600 + 23.6·T (ºC),  con silimanita     (96)[7]

Los experimentos de Goldsmith (1980) fueron conducidos a alta T (>900 ºC) por necesidades cinéticas, persiguiendo acotar de manera lo más precisa posible el equilibrio mediante inversiones en la dirección de la reacción. En las aplicaciones prácticas del barómentro GASP, esto introduce una fuente incertidumbre adicional a la del propio calibrado experimental, ya que hay que hacer una extrapolación a temperaturas propias del metamorfismo, generalmente menores de 800 ºC. Debido a esta fuente de error, se reconoce una incertidumbre de ±3 kbar para las presiones calculadas con este calibrado.

Más recientemente, Koziol y Newton (1988) han calibrado la reacción entre las fases puras contando con mejoras técnicas que permiten reducir el error experimental. Además, aunque los experimentos se realizaron a alta P y T (>900 ºC y >18 kbar), estos autores localizan un punto de la reacción a baja P y T (650 ºC y entre 14-15 kbar, obtenido a partir de los calibrados experimentales de las reacciones 2Zo+Ky+Qz=4An+H2O y 4Zo+Qz=5An+Grs+2H2O, Figura 8b) que permite reducir sustancialmente la incertidumbre debida a la extrapolación de la reacción entre las fases puras al rango P-T propio del metamorfismo cortical. La incertidumbre asignada por Koziol y Newton (1988) es de ±650 bar a 600 ºC y ±400 bar a 1000 ºC. Los calibrados de la reacción entre las fases puras con distena y silimanita que ofrecen estos autores son (Figuras 8b y 9):

P^O (bar) = -1093 + 22.80·T (ºC) con distena     (97)

P^O (bar) = -25 + 23.41·T (oC) - 0.0001872·T² (ºC) con silimanita     (98)

En la Figura 9 puede apreciarse que el equilibrio estable entre las fases puras ocurre en el campo de la distena, y, consecuentemente, el equilibrio con silimanita es metaestable. A partir de las ecuaciones (97) y (98) pueden extraerse los incrementos de las propiedades termodinámicas de las reacciones entre las fases puras. El procedimiento es idéntico al realizado anteriormente para los calibrados del termómetro biotita-granate, esto es, se asume que DCp_r = 0 y DV_r(P,T) = constante. Como ejemplo, analizaremos la reacción con distena. En primer lugar hay que transformar la ecuación (97) para expresar T en grados Kelvin; despejando T (ºC) en (97), sumando 273.15 ºC y volviendo a despejar para P obtenemos:

P^O_ky (bar) = -7320.8 + 22.80·T (K)     (97b)

Considerando que el incremento de volúmen para la reacción con distena es DV_r^o(1,298)=6.605 J/mol·bar (calculado a partir de los datos termodinámicos de Holland y Powell, 1990), y teniendo en cuenta que en el equilibrio entre los componentes puros K_eq=1 (i.e., R·T·lnK_eq=0), tenemos, reordenando (97b) y multiplicando por DV_r^o(1,298):

0 = (6.605)·7320.8 - (6.605)·22.80·T + (6.605)·P^o_ky + R·T·ln(1)                            

0 = 48353.9 - 150.69·T + 6.605·P^O_ky     (99)

de donde se deduce que DH_r^o(1,298)=48353.9 J/mol y DS_r^o(1,298)=150.69 J/mol·K. Sustituyendo estos valores en la ecuación (49) se obtiene la expresión barométrica:

0 = 48353.9 -150.69·T (K) + 6.605·P + R·T·lnK_eq      (100)

que puede despejarse para P si las funciones explícitas de las actividades de grosularia y anortita no dependen de P (lo cual no es el caso, como veremos más adelante). La solución gráfica de este calibrado se presenta en la Figura 9. Puede apreciarse que las isopletas de K_eq son lineas con pendiente dP/dT baja:

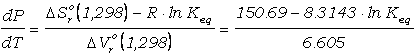     (101)

que varía de 22.8 bar/grado para K_eq=1 hasta 11.2 bar/grado para K_eq=10000 (en este caso el equilibrio con distena es metaestable, como se ilustra en la Figura 5, por lo que no ha sido representado en la Figura 9). Un procedimiento idéntico puede seguirse para las reacciones con silimanita y andalucita (ver Figura 5, donde la función que describe el equilibrio no es lineal en P y T ya que incluye los incrementos de capacidad calorífica, expansión térmica y compresibilidad isoterma).

De la ecuación (100) puede deducirse que el aumento de presión (a T constante) implica disminuir el valor de K_eq (Figuras 5 y 9), lo que supone aumentar los valores X_Ca^Grt, disminuir X_an, o ambos. Esto es lo que ocurre en las rocas naturales, donde se observa que a medida que aumenta la presión de equilibramiento, el granate es más rico en grosularia y la plagioclasa en albita. No obstante, este criterio cualitativo no es aplicable en sentido estricto ya que, en sistemas naturales multivariantes la composición de las fases es dependiente de P, T y de la composición del sistema. Así, rocas ricas en Ca presentarán granate y plagioclasa ricos en Ca, y es posible encontrar rocas equilibradas bajo las mismas condiciones P-T con composiciones de las fases contrastadas, aunque la constante de equilibrio debe ser la misma.

Modelos de Actividad de Granate y Plagioclasa

Ghent (1976) mostró la aplicabilidad del barómetro GASP en asociaciones metapelíticas de medio y alto grado, si bien, ante la ausencia de modelos de solución asequibles para el granate y plagioclasa consideró un comportamiento ideal para ambas fases (i.e., a_grs=X_Ca^Grt y a_an=X_an). Este autor indicó que los datos experimentales obtenidos por Ganguly y Kennedy (1974) en granates naturales y por Orville (1972) en plagioclasa indican que las actividades de grosularia en concentraciones diluidas y de anortita y albita son mayores que sus fracciones molares. Aunque la no consideración de estos comportamientos no ideales supone infraestimar las estimaciones de P en el primer caso (granate) y sobreestimarlas en el segundo (plagioclasa), Ghent (1976) sugirió que ambos efectos parecen cancelarse mutuamente, por lo que las estimaciones realizadas por Ghent (1976) considerando las soluciones ideales en distintas asociaciones naturales coinciden aproximadamente con las predecibles a partir de los campos de estabilidad de los polimorfos de Al₂SiO₅. Con posterioridad a Ghent (1976), la mayoría de las aplicaciones de este barómetro han considerado modelos de mezcla no ideales.

La solución sólida de granate suele describirse mediante modelos de mezcla generales, de tipo iónico multiposicional, como los presentados más arriba (ec. 53). En estos modelos, la función de actividad de la grosularia que debe sustituirse en la ecuación (94) es:

a_grs=X_grs³·g_grs³     (102)

ya que la multiplicidad de la posición estructural donde se mezcla el Ca es 3, según se ha definido la reacción en la ecuación (36).

Lo mismo puede decirse de la solución sólida de plagioclasa, aunque en este caso existen complicaciones adicionales derivadas de su estado de ordenamiento y del principio de Al-avoidance. Según este principio, la mezcla en las posiciones tetraédricas no es completamente azarosa, de forma que que la estructura de la plagioclasa no presentaría enlaces Al-O-Al encadenados, lo cual supone modificar la expresión de la entropía de mezcla iónica ideal (Kerrick y Darken, 1975; Tema 3). Ejemplos de modelos de soluciones binaria (ab-or) y ternaria (ab-an-or) son Saxena y Ribbe (1972), Newton et al. (1980), Newton y Haselon (1981), Hodges y Spear (1982), Ghiorso (1984), Green y Usdansky (1986), Fuhrman y Lindsley (1988) y Elkins y Grove (1990). En el caso del modelo de Fuhrman y Lindsley (1988), la expresión de a^an es:

a^an = [Xan·(1 + Xan)2/4]· exp{(Wor-ab[XabXor(0.5-Xan-2Xab)] + Wab-or[XabXor(0.5-Xan-2Xor)] +
+ Wor-an[2XorXan(1-Xan)+XabXor(0.5-Xan)] + Wan-or[Xor2(1-2Xan)+XabXor(0.5-Xan)] +
+ Wab-an[2XabXan(1-Xan) + XabXor(0.5-Xan)] + Wan-ab[Xab2(1-2Xan) + XabXor(0.5-Xan)] +
+ Wor-ab-an[XorXab(1-2Xan)])/(R·T)}        (103)

donde los valores de los parámetros de Margules W son funciones de P y T: W^G=W^H-T·W^S+P·W^V (W^H, W^S y W^V se asumen constantes independientes de P, T y la composición). Como puede apreciarse, en este modelo de mezcla las relaciones a-X no son del tipo a_i=X_i·g_i. Esto se debe a que el término ideal de la actividad de la anortita, que es el primer factor del lado derecho de la expresión que multiplica al exponencial (i.e., al coeficiente de actividad), resulta del principio de Al-avoidance mencionado anteriormente.

La utilización de modelos de mezcla como el anterior, donde la actividad de los componentes depende explícitamente de P y T, hace necesario despejar P de la función de K_eq para obtener una solución de presión.

Notas