La Condición de Equilibrio Heterogéneo
El principio físico-químico que subyace a los
cálculos termobarométricos, y a todos los cálculos basados en la termodinámica
del equilibrio, es el principio de estabilidad de Gibbs. Este criterio
establece que un sistema está en equilibrio estable cuando su energía libre de
Gibbs (G) está minimizada,
esto es, G no puede variar y dG=0.
Del criterio de estabilidad de Gibbs y de la
definiciones de las energías interna (U) y libre de Gibbs de un sistema:
Usis = T·S -
P·V +
S(mi·ni)
(1)
Gsis = U - T·S + P·V =
S(mi·ni)
º Mínimo
(2)
donde
mi y ni
son los potenciales químicos y moles, respectivamente, de los i componentes
del sistema, resulta:
dUsis = T·dS
- P·dV +
S(mi·dni)
(3)
0 = S·dT
- V·dP + S(ni·dmi)
(ec. de Gibbs-Duhem, 4)
dGsis =
d(U-T·S+P·V) = -S·dT + V·dP +
S(mi·dni)
= 0.
(5)
El principio de
estabilidad de Gibbs implica que los posibles procesos que tengan lugar en el
sistema deben ser isotermos e isobáricos, por lo que:
dGsis =
S(mi·dni)
= 0. (6)
Dada la naturaleza
extensiva de G, la energía libre de un sistema heterogéneo es la suma de las
energías libres de las fases constitutivas del sistema:
Gsis =
S(mi·ni)
= SGj,
(7)
donde Gj
representa la energía libre de cada fase j, que se define como:
Gj =
S(mk·nk)j,
(8)
donde
mk y nk
son los potenciales químicos y moles, respectivamente, de los k componentes
de la fase j. En consecuencia la condición de equilibrio heterogéneo puede
reescribirse como:
Gsis =
S(mi·ni)
= SGj =
S(mk·nk)j
º Mínimo
(9)
dGsis =
S(mi·dni)
= SdGj
= S(mk·dnk)j
= 0.
(10)
La expresión de Gsis y dGsis
en función de los potenciales químicos y moles de componentes de fase (mkj
y nkj) en lugar de componentes del sistema es conveniente
en nuestro caso ya que estamos interesados en la evaluación de la condición de
equilibrio en un sistema que sufre procesos de reacción isotermos e isobáricos
entre fases. Estas reacciones se escriben entre especies químicas puras cuya
estequiometría y estructura corresponden a las de las fases en las que se
encuentran diluidas (i.e., componentes de fase), y cuyas propiedades
termodinámicas (i.e., los estados estándar), necesarias para evaluar la
condición de equilibrio, pueden obtenerse con fiabilidad.
Supongamos una reacción entre un determinado
conjunto de componentes de fase A, B, C y D, que se encuentran diluidos en las
fases a,
b,
c, y
d, respectivamente, en un
sistema cualquiera. Podemos escribir la reacción como:
naAa
+ nbBb
= ncCc
+ ndDd
(11)
0 =
ncCc
+ ndDd
- naAa
- nbBb
(12)
En estas ecuaciones,
na, ...
corresponden a los coeficientes estequiométricos de los componentes de fases A,
... diluidos en las fases a,
... Aplicando la condición de equilibrio (10) al sistema en cuestión, que sufre
un proceso de reacción isotermo e isobárico, obtenenos:
dGsis = (mA·dnA)a
+ (mB·dnB)b
+ (mC·dnC)c
+ (mD·dnD)d
= 0
(13)
La estequiometría de la
reacción (11) requiere que por cada
na moles del
componente de fase A que se consumen deben consumirse exactamente
nb moles de B y
producirse nc
moles de C y nd
moles de D. Esto implica que los cambios diferenciales en los moles de los
componentes de fase (dnA,...) no son independientes sino que guardan
una relación de proporcionalidad, definida como:
dnAa/-na
= dnBb/-nb
= dnCc/nc
= dnDd/nd
= dx
(14)
En esta relación la
variable x describe el
número de moles de reactantes y productos que han reaccionado, y se denomina
progreso de la reacción. Expresando dnAa,
... en función de dx y
sustituyendo en (13), se obtiene:
dGsis = (-na·mAa
- nb·mBb
+ nc·mCc
+ nd·mDd)·dx
= 0
(15)
En un sistema en
equilibrio no pueden darse reacciones que produzcan cambios en la energía libre
del sistema. Por lo tanto, el cambio en la energía libre del sistema respecto
del cambio en la variable de progreso
x debe ser 0.
Matemáticamente esto se expresa diferenciando la ecuación (15):
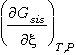 = -na·mAa
- nb·mBb
+ nc·mCc
+ nd·mDd
= 0 (16)
= -na·mAa
- nb·mBb
+ nc·mCc
+ nd·mDd
= 0 (16)
Esto es, la condición
de equilibrio de un sistema necesita que la relación anterior (16) entre los
potenciales químicos de los componentes de fase A,... sea válida. Puede
apreciarse que esta relación es idéntica a existente entre los componentes de
fase que definen la relación de reacción estequiométrica (12). En la derivación
anterior no se ha impuesto ninguna restricción a la formulación de la reacción,
por lo que la reacción (12) y la condición de equilibrio (16) pueden formularse
de forma general:
Para cualquier reacción química balanceada que pueda
escribirse entre todos o parte de los componentes de fase de
una asociación de fases en equilibrio como:
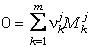 (17)
(17)
existe una relación equivalente entre los potenciales
químicos de los componentes de fase implicados en la reacción:
 (18)
(18)
donde
nkj
son los coeficientes estequiométricos (por convenio, positivos en el lado
derecho y negativos en el lado izquierdo de la reacción) asociados a cada
fórmula-gramo Mkj de los k=1..m componentes de las j fases
implicadas en la reacción, mkj
son los potenciales químicos de esos componentes de fase, y
DGr(P,T,X) es el
incremento de energía libre debido a la reacción (=0 por la condición de
equilibrio), bajo condiciones P, T y composiciones de las fases (X)
determinadas.
La formulación general del equilibrio
heterogéneo (18) es una de las ecuaciones de la Termodinámica con mayor utilidad
en el estudio de los sistemas heterogéneos de interés geológico. De hecho, la
termobarometría se fundamenta totalmente en esta ecuación.
Ecuación Termobarométrica Fundamental
La aplicación práctica de la ecuación (18)
necesita de formulaciones explícitas para los potenciales químicos de los
componentes de fase implicados en las reacciones balanceadas. El potencial
químico de un componente k en una fase
a puede expresarse como
una función de P, T y de la composición (X) de la fase como:
mka
= mko + R·T·ln aka
(19)
donde R es la constante
de los gases perfectos y T es la temperatura absoluta. La ecuación (19)
representa una expansión de la función
mka
en dos funciones.
· La
primera de ellas, mko,
representa la energía libre molar total de la fase en el caso límite en que ésta
esté constituida exclusivamente por el componente k (i.e., Xka=1
o nj¹ka
= 0), de manera que mka(Xk=1)=mko=Gko.
Esta función es dependiente de P y T e independiente de la composición, y
define el estado estándar para la solución. Los estados estándar se
eligen en función del problema a resolver. Por ejemplo, el estado estándar
generalmente utilizado para las fases sólidas es el definido por las propiedades
del componente k en estado puro, isoestructural con
a a P y T de interés,
mientras que para los fluidos es el definido por las propiedades del componente
k en estado puro a 1 bar y T de interés.
· La
segunda función del lado derecho de la ecuación (19) define la actividad
del componente k en la fase, aka.
Esta es una función de P, T y la composición de la fase, y puede definirse como
la función que permite describir las variaciones del potencial químico cuando la
composición de la solución sólida se desplaza del término extremo k. De la
igualdad (19), es aparente que la función de actividad depende del estado
estándar elegido:
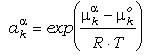 (20)
(20)
El estado estándar para los sólidos,
mko(P,T),
será el considerado en las ecuaciones que siguen. Las funciones de actividad (o
relaciones actividad-composición, a-X) suelen expresarse como el producto de un
término dependiente exclusivamente de la composición (i.e., la fracción molar Xka)
y otro término dependiente de P, T y X denominado coeficiente de actividad,
gka,
de manera que:
aka
= Xka·gka.
(21)
Sustituyendo la ecuación (19) en la ecuación
general del equilibrio heterogéneo (18) obtenemos:
DGr(P,T,X) =
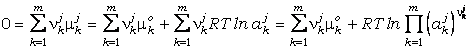 (22) (22)
o de manera más
compacta:
DGr(P,T,X) = 0 =
Dmro(P,T)
+ R·T·lnKeq(P,T,X) (23)
donde
Dmro(P,T)
es el cambio de energía libre molar asociada a la reacción entre las fases puras
a P y T de interés (i.e., condiciones del estado estándar seleccionado):
Dmro(P,T)
º
DGro(P,T)
(24)
y Keq(P,T,X)
es la constante de equilibrio:
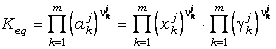 (25)
(25)
La relación definida
por la ecuación (23) es la base de los cálculos termobarométricos (y otros
muchos cálculos termodinámicos), puesto que esta relación indica que existe
un valor de Keq que satisface la ecuación para cada condición P-T
determinada. Dicho de otro modo, el uso de equilibrios con fines
termobarométricos implica resolver la ecuación (23) para P o T conociendo las
composiciones de las fases sólidas analizables en una roca.
Para poder solucionar la ecuación (23) conocida
Keq debe poder evaluarse el incremento de energía libre de reaccion
entre las fases puras a P y T de interés. Esto se realiza expresando
DGro(P,T)
en términos de otras funciones de estado. Puesto que para cualquier fase pura
compuesta por el componente de fase k:
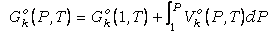 ,
(26) ,
(26)
donde Gko(1,T)
es la energía libre de la fase pura a 1 bar y T de interés y Vko(P,T)
es el volumen de la fase pura a P y T de interés, la ecuación (23) puede
reescribirse (reordenando las funciones para las especies presentes en la fase
fluida):
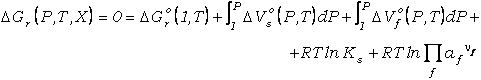 (27)
(27)
donde los subíndices s
y f se refieren a componentes de fases sólidas y fluida, respectivamente.
La integral de la función de volumen para las
fases sólidas puede evaluarse considerando el volumen de las fases puras a 1 bar
y 298.15 K (Vso(1,298)) y los factores de expansión
térmica isobárica (a) y
compresibilidad isoterma (b)
según la ecuación:
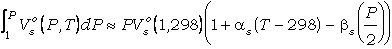 (28)
(28)
(e.g., Powell, 1978;
Holland y Powell, 1990), o mediante funciones polinómicas empíricas que expresan
el volumen de las fases en función de P y T (e.g., Berman, 1988).
Actualmente se dispone de estos datos para un gran número de fases puras de
interés geológico, que pueden encontrarse en bases de datos termodinámicos
(e.g., Helgeson et al., 1978; Robie et al., 1978; Berman, 1988; Holland y
Powell, 1990).
La integral de volúmen de los componentes puros
de la fase fluida a P y T de interés se evalúa mediante la relación:
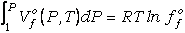 (29)
(29)
donde ffo
es la fugacidad del componente puro f del fluido a P y T de interés, que puede
evaluarse mediante funciones de estado específicas (e.g., de tipo Redlich-Kwong)
o mediante expresiones polinómicas empíricas (e.g., Holland y Powell, 1985,
1990).
Por otra parte, la energía libre de las fases a
1 bar y T de interés puede expresarse en función de la entalpía y entropía según
la ecuación:
Gko(1,T)
=
Hko(1,T)
- T·Sko(1,T) (30)
donde Hko(1,T)
y Sko(1,T) son las entalpía y entropía de la fase pura a 1
bar y T de interés, que se calculan mediante las expresiones:
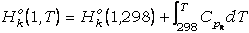 (31)
(31)
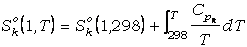 (32)
(32)
donde Hko(1,298),
Sko(1,298) son las entalpía y entropía de formación (o
aparentes de formación) de la fase pura a 1 bar y 298.15 K, que pueden
encontrarse en las bases de datos termodinámicos mencionadas más arriba, y Cpk
es la capacidad calorífica a presión constante, que se expresa como funciones
polinómicas de T (e.g., del tipo Maier-Kelley) con un número de términos
variable, por lo general no superior a 5. Los coeficientes de estas funciones
también se pueden encontrar tabulados en las bases de datos termodinámicos
existentes.
Sustituyendo (28)-(32) en la ecuación (27)
queda finalmente la expresión:
 (33)
(33)
donde los subíndices s,
f, y r aplican a las propiedades de componentes de las fases sólidas, de la fase
fluidas, y de reacción, respectivamente.
La ecuación (33) puede resolverse para T o P a
partir de una estimación de la constante de equilibrio conociendo los
incrementos de las propiedades termodinámicas asociados a la reacción. A su vez,
la constante de equilibrio es evaluable si se conocen las relaciones entre la
actividad de los componentes y la composición de las fases, i.e., las relaciones
a-X o modelos de actividad.
Notas
Las
relaciones derivadas de la consideración de equilibrio son aplicables tanto a
sistemas homogéneos como heterogéneos, aunque en estas notas consideramos
exclusivamente los últimos.
[Back] [Home] [Up] [Next]
Última
modificación:
domingo, 05 de octubre de 2025 15:27 +0200 |