|
Existen muchos equilibrios que han sido
calibrados con fines termobarométricos en los últimos 25 años. Muchos de
ellos permiten obtener buenos resultados, siempre y cuando no se apliquen
fuera de los límites P-T-X de la calibración. Obtener buenos resultados
implica conocer las bases conceptuales de las calibraciones, para poder
juzgar sus límites de aplicabilidad. Además, cualquier esfuerzo destinado a
obtener estimaciones de P y T en rocas naturales debe así mismo considerar
sus incertidumbres. De forma general, los criterios de selección de
equilibrios con fines termométricos y barométricos se basan en las
propiedades termodinámicas de los equilibrios y el grado de conocimiento de
las variables implicadas en la ecuación (33).
La identificación del equilibrio en una
asociación de fases es un aspecto de importancia fundamental que debe ser
considerado previamente a cualquier intento de obtener soluciones
termobarométricas. Es obvio que los resultados numéricos obtenidos en rocas
donde no exista equilibrio entre todas o parte de las fases que la forman
carecen de significado geológico alguno.
Los criterios que pueden utilizarse para
juzgar el requisito fundamental de equilibrio son texturales,
composicionales y teóricos. No consideraremos aquí estos criterios en
detalle. Los requisitos más importantes que permiten concluir que una
asociación de fases está presumiblemente en equilibrio son:
-
Texturas de recristalización (e.g.,
agregados poligonales).
-
Ausencia de texturas reaccionales
(e.g., bordes de reacción), incluyendo ausencia de zonación en fases que
se encuentren en contacto mutuo.
-
Partición elemental sistemática entre
fases que comparten componentes (discutida más adelante).
-
No violación de la regla de las fases.
Existen muchos casos en que estos
requisitos son cumplidos, y las aplicaciones termobarométricas tienen
validez geológica. Sin embargo, existen casos en que estos requisitos no se
cumplen y el equilibrio no puede asumirse. En estos casos no hay que
empecinarse en obtener soluciones termobarométricas a toda costa. Hay
que reconocer que las soluciones numéricas obtenidas en estas rocas pueden
ser justificadas mediante los conceptos de equilibrio local o parcial,
particularmente si coinciden con evidencias o intuiciones geológicas,
pero la incertidumbre es en todo caso elevada. Más adelante, volveremos a
discutir estos aspectos utilizando ejemplos concretos.
Partiendo del requisito fundamental de
equilibrio en una asociación de fases determinada, el número de
equilibrios que potencialmente pueden utilizarse con fines
termobarométricos es muy elevado. Esto resulta del hecho de que, en
principio, la obtención de las condiciones de equilibramiento P-T-X de
la roca se basa en la aplicación de la ecuación (33) para cualquiera
de los equilibrios que puedan escribirse entre
todos o parte de los componentes de fase de la asociación de fases. En
un sistema con i componentes del sistema y k componentes de fase, el
número de reacciones balanceadas posibles que pueden definirse viene
dado por la fórmula combinatorial:
nº de posibles equilibrios =
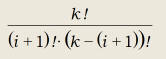 (34) (34)
Por ejemplo, en un sistema de
sólo 8 componentes (e.g.,
KNaCaFMASH) formado por una asociación divariante de 8 fases (e.g., Qtz,
Ms, H2O, Grt, Bt, St, Pl, Als) descritas por 14 componentes
de fase (e.g., qtz, ms, pa, H2O, alm, prp, grs, ann, phl,
Fe-st, Mg-st, ab, an, als), el número de equilibrios posibles y
potencialmente utilizables es 2002 (aunque las degeneraciones del
sistema hacen que el número real sea menor). De entre todos los
equilibrios posibles, sólo k-i son linealmente independientes (en el
ejemplo utilizado, 14-8=6). Cualquier otra reacción del conjunto total
puede ser generada por combinaciones del subconjunto linealmente
independiente, aunque éste último no es único. Por tanto, una
caracterización termobarométrica completa de una roca determinada
debería incluir la evaluación de un subconjunto de equilibrios
linealmente independiente. Sin embargo, la práctica habitual consiste en
evaluar un número más limitado de equilibrios, generalmente 2 ó 3.
Dado que nuestro interés es resolver la
ecuación (33) para P (a T dada) o para T (a P dada) conociendo la
constante de equilibrio para una reacción determinada, el primer
criterio de selección de equilibrios termobarométricos para cualquier
asociación de fases es el poder estimar lo más fiablemente posible la
constante de equilibrio.
Consecuentemente, los equilibrios
termobarométricos seleccionados deben ser aquellos en que no intervengan
componentes de la fase fluida (e.g., H2O, O2,...)
ya que la composición de esta fase no es obtenible, generalmente, por
métodos analíticos directos. De hecho, todos los equilibrios
termobarométricos son del tipo sólido-sólido, para los que Keq
se calcula directamente a partir de la composición de las fases sólidas
analizada con métodos apropiados (e.g., microsonda). Es este caso, los
términos de fugacidad y actividad de los componentes en la fase fluida
de la ecuación (33) son innecesarios.
Otros criterios discutidos más adelante
justifican igualmente la exclusión de equilibrios sólido-fluido para
fines termobarométricos. Debe notarse que los equilibrios sólido-fluido
se utilizan para estimar la composición de la fase fluida en equilibrio
con las fases sólidas durante el metamorfismo, previo conocimiento de P
y T.
La constante de equilibrio es una
función natural de T-1, como puede apreciarse despejando lnKeq
en (23):
 (35)
(35)
Aunque en esta ecuación no aparece explícitamente la dependencia de Keq
de la presión, esta dependencia queda clara de las ecuaciones (26) y
(33). Por tanto, la ecuación (35) es la ecuación de una superficie en el
espacio lnKeq-1/T-P.
Para ejemplificar estas relaciones
utilizaremos dos equilibrios termobarómetricos aplicables en
metapelitas, el equilibrio entre granate, cuarzo, distena y plagioclasa,
representado por la reacción entre los componentes de fase anortita
(an), grosularia (grs), silicato de Al (als) y cuarzo (qtz), denominado
comumnente barómetro GASP:
Ca3Al2Si3O12
(grs) + 2Al2SiO5 (als) + SiO2 (qtz)
= 3CaAl2Si2O8
(an) (36)
y el equilibrio entre granate y biotita que puede expresarse mediante la
reacción entre los componentes de fase almandino (alm), piropo (prp),
annita (ann) y flogopita (phl), denominado termómetro
biotita-granate o GARB:
Fe3Al2Si3O12
(alm) + KMg3AlSi3O10(OH)2
(phl) =
= Mg3Al2Si3O12
(prp) + KFe3AlSi3O10(OH)2
(ann) (37)
La Figura 1
ilustra las relaciones lnKeq-1/T-P
para el barómetro GASP. La superficie representada en esta figura ha
sido calculada solucionando la ecuación (33) para el equilbrio GASP con
distena, utilizando los datos termodinámicos internamente consistente de
Holland y Powell (1990). Nótese que se incluyen tres superficies
independientes de K que corresponden a los equilibrios Ky=And, Ky=Sill y
And=Sill, y que la superficie correspondiente al equilibrio GASP
presenta una parte estable (en el campo de distena) y una extensión
metaestable (en los campos de andalucita y sillimanita). En la parte
estable de esta superficie se han dibujado las líneas de iso-lnKeq,
que a su vez han sido proyectadas sobre el plano 1/T (o T)-P. En la Figura 1
sólo se ha representado la superficie correspondiente al equilibrio GASP
con distena para facilitar su visualización, aunque una proyección
completa sobre el plano P-T, incluyendo las secciones estables de las
curvas iso-Keq de los equilibrios con distena, sillimanita y
andalucita, se presenta más adelante (Figura 5).
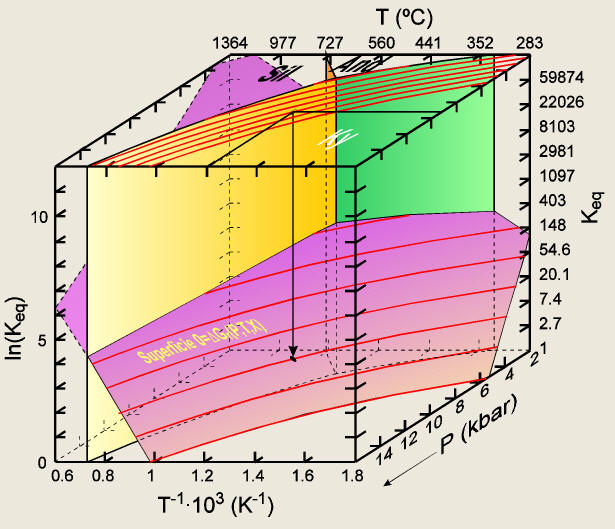
Figura
1. Superficie lnKeq-1/T-P
para el equilibrio GASP con distena (ec. 36) calculada a partir de
la ecuación (33) con los datos termodinámicos de Holland y Powell
(1990). Se muestran además de las tres superficies que definen los
equilibrios Ky=Sil, Ky=And y And=Sil (independientes de Keq
) que permiten definir la sección estable y la extensión metaestable
del equilibrio GASP con distena. La extensión estable ha sido
delineada con curvas de iso-lnKeq
, que también se han proyectado en el plano P-1/T (o P-T).
El método para obtener una solución barométrica se
ilustra también en la Figura 1. Queda
claro de esta figura que existe un valor único de Keq
para cada par de valores P-T, por lo que conocida Keq y
disponiéndose de una estimación independiente de T, obtenemos la
solución barométrica. Relaciones similares pueden obtenerse para el
termómetro GARB, que puede utilizarse para obtener una solución
termométrica conociendo Keq si se dispone de una estimación
independiente de P. La aplicación práctica de estos dos equilibrios en
rocas determinadas se ilustra más adelante.
Dependencia de T de la Constante de Equilibrio: Secciones
Isobáricas
La dependencia de Keq
respecto de T y P puede evaluarse a partir de la ecuación (35)
diferenciando lnKeq
respecto de T a P constante, y de P a T constante, respectivamente. Esto
es equivalente evaluar las superficies lnKeq-1/T-P
en secciones isobáricas e isotermas. Consideremos en primer lugar
secciones isobáricas, que son indicativas de la adecuación del
equilibrio a fines termométricos ya que describen la dependencia
de Keq respecto de T. Diferenciando (35) respecto de T,
obtenemos:
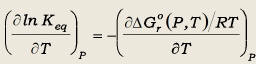 (38)
(38)
que puede solucionarse sustituyendo
DGro(P,T)
=
DHro(P,T)
- T·DSro(P,T)
(30b)
(cf. eq.
30) en (38):
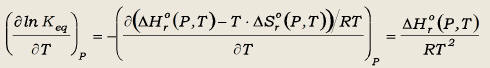 (39)
(39)
que es la ecuación de van’t Hoff, y diferenciado (35) respecto de 1/T:
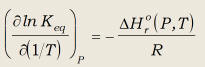 (40)
(40)
Las ecuaciones
(39) y (40) indican que, a P constante, lnKeq, y por lo tanto
Keq, es dependiente del incremento de entalpía de la reacción
entre las fases puras. Esta dependencia se expresa matemáticamente
mediante las pendientes de las rectas tangentes a la curva lnKeq-1/T
a P constante, cuyos valores son
-DHro(P,T)/R
(evaluados a P y T de interés), como se deduce de la ecuación (40) y de
la sustitución de la ecuación (30b) en (35):
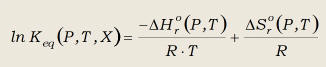 (41)
(41)
que indica, además, que la intersección en el origen de las rectas
tangentes es
DSro(P,T)/R.
Las relaciones anteriores pueden apreciarse en la Figura 2, donde
se han proyectado las secciones isobáricas a 8 kbar correspondientes a
los equilibrios GASP estables (con Ky y Sil) y GARB. Una primera
observación que puede realizarse de esta figura es que las curvas lnKeq
¾1/T para estos equilibrios
son prácticamente rectas. Una explicación para este comportamiento se dará más
adelante.
De lo dicho anteriormente puede
concluirse que los equilibrios utilizables con fines termométricos, esto
es, aquellos en que Keq
presente una fuerte dependencia de T,
deben presentar
fuertes incrementos de entalpía de reacción entre los componentes
puros.
Esto garantiza que las líneas de iso-Keq
(isopletas) de reacción en el espacio P-T estarán fuertemente
apretadas, lo cual es conveniente desde el punto de vista del minimización del error
en la estimación de T. Para ilustrar este
aspecto, consideremos dos equilibrios, r1 y r2, de forma que
DHr1o(P,T)<<DHr2o(P,T).
El error en la temperatura de equilibramiento inferida es
significativamente menor para r2 que para r1 para un mismo error en los
valores respectivos de Keq
(Keq(r1) y Keq(r2)), como se ilustra en la Figura 3.
De lo dicho anteriormente, la
observación de la
Figura 2 parece llevarnos a una contradicción: las
pendientes de las curvas GASP son mayores que las de la curva GARB, a
pesar de que este último equilibrio se utiliza con fines termométricos y
el anterior no. Esta contradicción es solo aparente, ya que las
constantes de equilibrio y las propiedades termodinámicas de ambos
equilibrios no son comparables. Así, el incremento de entalpía (y la
pendiente) es función del número de moles de componentes implicados en
la reacción. Si, por ejemplo, el equilibrio GARB se escribe con 2 moles
de cada componente en lugar de 1, el incremento de entalpía se
multiplica por dos, y la pendiente aumenta. Debe notarse que la
constante de equilibrio también se ve modificada, ya que las actividades
de los componentes deben elevarse a dos, por lo que la relación entre
lnKeq y
DHro(P,T)
no se modifica. En consecuencia, para llegar a conclusiones al respecto
de la adecuación de equilibrios a fines termométricos, es necesario
considerar equilibrios que efectivamente sean comparables. Por ejemplo,
pueden compararse dos reacciones de intercambio siempre que el número de
cationes intercambiados sea el mismo en ambos casos.
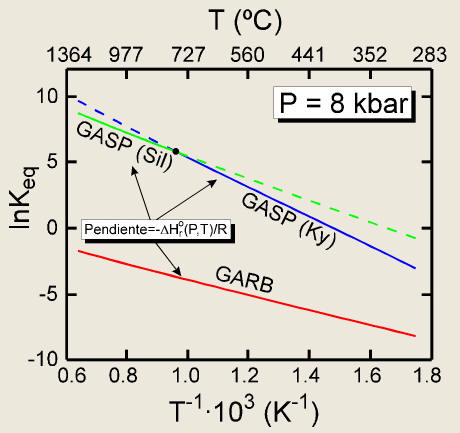
Figura
2. Sección isobárica (8 kbar) lnKeq-1/T
para los equilibrios GASP estables (i.e., con distena y sillimanita;
extensiones metaestables en línea discontínua) y GARB, con
indicación de la pendiente a P y T dadas. Nótese que las curvas son
prácticamente rectas.
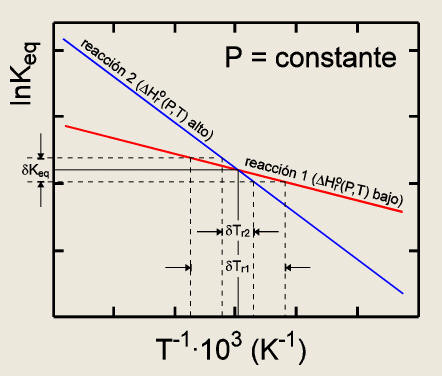
Figura
3. Sección isobárica lnKeq-1/T
esquemática que ilustra el efecto del error en la determinación de Keq.(dKeq.)
sobre los errores en las estimaciones de T (dT)
a partir dos reacciones, r1 y r2, con incrementos de entalpía bajo y
alto, respectivamente.
Dependencia de P de la
Constante de Equilibrio: Secciones Isotermas
La evaluación de secciones isotermas es
indicativa de la adecuación del equilibrio a fines barométricos,
ya que describen la dependencia de Keq respecto de P.
Diferenciando (35) respecto de P:
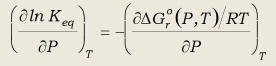 (42)
(42)
que puede evaluarse considerando la relación (26), de manera que:
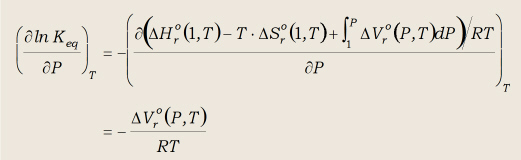 (43)
(43)
Esta ecuación indica que, a T constante, lnKeq, y por lo
tanto Keq, es dependiente del incremento de volumen de la
reacción entre las fases puras.
Así, los equilibrios con fines barométricos, esto es, aquellos en que Keq
presente una fuerte dependencia de P,
deben presentar fuertes incrementos de volumen de
reacción
lo que garantiza que las isopletas de Keq en el espacio P-T
estarán fuertemente apretadas. Al igual que para el caso
discutido anteriormente al respecto de la dependencia de Keq
respecto de la temperatura, esto es conveniente desde el punto de vista
de la minimización del error en la estimación de P. Puede
demostrarse igualmente que las estimaciones de P inferidas de
equilibrios con fuertes incrementos de volumen son menos sensibles a
errores en la estimación de Keq que aquellas inferidas de
equilibrios con DVro(P,T)
pequeños.
Estas relaciones pueden apreciarse en
la
Figura 4, donde se han proyectado las secciones isotermas a 700
ºC correspondientes a los equilibrios GASP estables (con Ky, Sil y And)
y GARB. De nuevo, se observa que las curvas lnKeq-P
para estos equilibrios son prácticamente rectas, lo cual será explicado
más adelante. Por otra parte, es claro que la dependencia del equilibrio
GARB respecto de la presión es prácticamente nula, y cualquier error en
la estimación de Keq resultará en una incertidumbre muy
elevada en la presión calculada, por lo que su utilización como
barómetro debe descartarse. Por contra, los equilibrios GASP sí muestran
esta dependencia, y pueden utilizarse para extraer información de
presión. La incertidumbre en las presiones calculadas debida a errores
en la estimación de Keq es menor en el equilibrio GASP con
distena y mayor en el equilibrio con andalucita, lo cual no es sino el
resultado de que en el primer caso el incremento de volumen es mayor que
en el segundo (la distena es más densa que la andalucita).
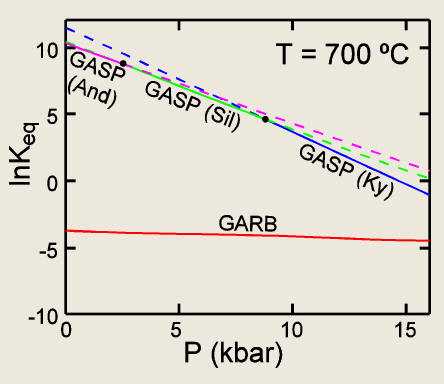
Figura
4. Sección isoterma (700 ºC) lnKeq-P
para los equilibrios GASP estables (i.e., con distena, sillimanita y
andalucita; extensiones metaestables en línea discontínua) y GARB.
Nótese que las curvas son prácticamenete rectas.
Aunque los equilibrios GASP muestran
una fuerte dependencia respecto de P, puede quedar la duda al respecto
de la utilización de estos equilibrios como termómetros o como
barómetros, dado que, como vimos anteriormente, también presentan
dependencia respecto de la temperatura. Este problema se resuelve
considerando simultáneamente los efectos de los incrementos de
entalpía y de volumen de reacción, lo cual es posible evaluando
secciones iso-Keq.
Los criterios anteriores al respecto de
la magnitud de los incrementos de entalpía y volumen de reacción que
garanticen isopletas de Keq fuertemente apretadas en el
espacio P-T pueden utilizarse para calificar los equilibrios como buenos termómetros
o buenos barómetros. No obstante, como acabamos de
comprobar, es necesario evaluar la importancia relativa de ambas
magnitudes, al menos en casos como el de los equilibrios GASP, que
muestran dependencias importantes respecto de T y P. La contribución
relativa de estas magnitudes controla la pendiente dP/dT de los
equilibrios en el espacio P-T (secciones iso-Keq), que viene
determinada por la ecuación de Clapeyron. Esta ecuación se obtiene
considerando la condición de equilibrio a P, T y X de interés:
dDGr(P,T,X)
= 0 = -DSr(P,T,X)·dT
+ DVr(P,T,X)·dP
(44)
que resultan en:
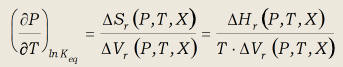 (45)
(45)
La ecuación (45)
indica que equilibrios con fuertes pendientes dP/dT deben presentar
altos incrementos de entalpía y entropía de reacción y/o bajos
incrementos de volumen de reacción, y los equilibrios con pendientes
dP/dT bajas deben presentar las relaciones contrarias. Por tanto,
las
estimaciones de T deben realizarse a partir de equilibrios
heterogéneos con pendientes dP/dT altas (i.e., tendiente a
¥) para
minimizar las incertidumbres debidas a errores en las estimaciones
independientes de P,
y,
las
estimaciones de P deben realizarse a partir de equilibrios
heterogéneos con pendientes dP/dT bajas (i.e., tendiente a 0) para
minimizar las incertidumbres debidas a errores en las estimaciones
independientes de T,
Estas relaciones
se ejemplifican en la Figura 5, donde se han proyectado las
secciones iso-Keq
correspondientes a los equilibrios GASP estables (con Ky, Sil y And) y
GARB. Ahora sí es posible disponer de una información completa al
respecto de las dependencias P-T-Keq y de la adecuación de
los distintos equilibrios a fines termométricos o barométricos, que, de
acuerdo con lo observado previamente, pueden resumirse como sigue:
·
las curvas en el espacio P-T para
estos equilibrios son prácticamente rectas,
·
la dependencia del equilibrio GARB
respecto de T es fuerte y prácticamente nula respecto de P, por lo que
debe utilizarse como termómetro,
·
los equilibrios GASP muestran
dependencia respecto de T y de P, aunque la última es más importante
(i.e., es más importante el efecto del incremento de volumen que el del
incremento de entalpía de reacción), por lo que su utilización debe ser
como barómetro.
·
para los equilibrios GASP, la
incertidumbre en las presiones calculadas debida a errores en la
estimación independiente de T es menor en a baja presión. Esto es debido al efecto combinado de
las entalpías y volumenes de reacción, e ilustra la necesidad de conocer
la razón DHr(P,T,X)/DVr(P,T,X)
a la presión y temperatura de interés para calificar la adecuación de un
equilibrio a fines termométricos o barométricos.
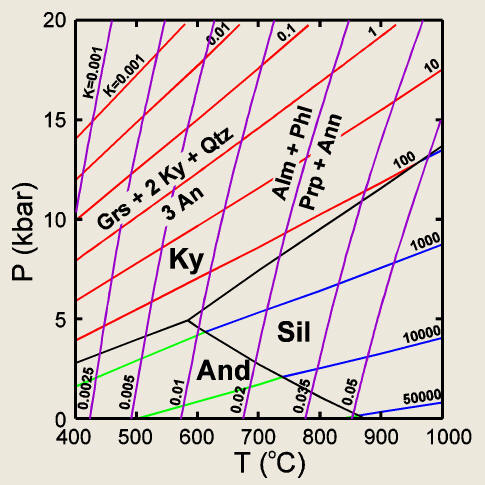
Figura
5. Proyección P-T de secciones isot-Keq
para los equilibrios GASP (con distena, sillimanita y andalucita) y
GARB. Nótese que las curvas son prácticamente líneas.
De las relaciones anteriores puede
concluirse que los buenos termómetros deben presentar, bajos incrementos de volumen de reacción (idealmente,
DVr(P,T,X) =
0) y fuertes incrementos de entalpía de reacción. Los equilibrios
de intercambio entre componentes con volumenes molares similares,
como el equilibrio de intercambio Fe-Mg entre biotita y granate, son, por
tanto, buenos termómetros. De hecho, la mayor parte de los equilibrios
termométricos utilizados son de este tipo (Tabla 1). Debe notarse que
los equilibrios más apropiados según este criterio son los termómetros de
intercambio isotópico (e.g., partición 18O/16O entre
silicatos), ya que los incrementos de volumen asociados a este tipo de
equilibrios pueden considerarse nulos (y en consecuencia la pendiente dP/dT
es infinita). No obstante, la aplicabilidad de estos equilibrios en rocas de
grado medio y alto es problemática, ya que las temperaturas de bloqueo
isotópico asociadas suelen ser muy inferiores a las temperaturas máximas
alcanzadas por las rocas.
Tabla 1.-
Termómetros de intercambio
|
Granate-Biotita |
Fe3Al2Si3O12
+ KMg3AlSi3O10(OH)2 =
Mg3Al2Si3O12 + KFe3AlSi3O10(OH)2 |
Thompson (1976b); Goldman y Albee
(1977); Ferry y Spear (1978); Hodges y Spear (1982); Perchuk y
Larent’eva (1983); Ganguly y Saxena (1984); Indares y Martignole
(1985); Hoinkes (1986); Berman (1990); Williams y Grambling (1990);
Bhattacharya et al. (1992). |
|
Granate-Cordierita |
2Fe3Al2Si3O12
+ 3Mg2Al4Si5O18 =
2Mg3Al2Si3O12
+ 3Mg2Al4Si5O18
|
Currie (1971); Hensen y Green (1973);
Thompson (1976b); Holdaway y Lee (1977); Martignole y Sisi (1981);
Perchuk y Larent’eva (1983); Bhattacharya et al. (1988). |
|
Granate-Clinopiroxeno |
Fe3Al2Si3O12
+ 3CaMgSi2O6 =
Mg3Al2Si3O12
+ 3CaFeSi2O6 |
Råheim y Green
(1974); Mori y Green (1978); Ellis y Green (1979); Saxena (1979);
Ganguly (1979); Dahl (1980); Powell (1985); Krogh (1988); Pattison y
Newton (1989); Ganguly y Bhattacharya (1987); Carswell y Harley
(1990); Green y Adam (1991); Perkins y Vielzeuf (1992). |
|
Granate-Ortopiroxeno |
Fe3Al2Si3O12
+ 3MgSiO3 =
Mg3Al2Si3O12
+ 3FeSiO3 |
Mori y Green (1978); Dahl (1979);
Harley (1984a); Sen y Bhattacharya (1984); Lee y Ganguly (1986,
1987); Carswell y Harley (1990); Bhattacharya et al., (1991). |
|
Granate-Olivino |
2Mg3Al2Si3O12
+ 3Fe2SiO4 =
2Fe3Al2Si3O12
+ 3Mg2SiO4 |
Kawasaki (1977);
O’Neil y Wood (1979,1980); Carswell y Harley (1990). |
|
Granate-Hornblenda |
4Mg3Al2Si3O12
+ 2NaCa2Fe4Al3Si6O22(OH)2
= 4Fe3Al2Si3O12 + 2NaCa2Mg4Al3Si6O22(OH)2
|
Graham y Powell
(1984). |
|
Granate-Clorita |
5Mg3Al2Si3O12
+ 3Fe5Al2Si3O10(OH)8
= 5Fe3Al2Si3O12 +
3Mg5Al2Si3O10(OH)8 |
Dickenson y Hewitt
(1986); Laird (1988); Grambling (1990). |
|
Granate-Fengita |
Mg3Al2Si3O12
+ 3KFeAlSi4O10(OH)2
= Fe3Al2Si3O12
+ 3KMgAlSi4O10(OH)2 |
Krogh y Raheim
(1978); Green y Hellman (1982); Hynes y Forest (1988); Carswell y
Harley (1990). |
|
Ortopiroxeno-Clinopiroxeno |
MgSiO3 +
CaFeSi2O6 =
FeSiO3 + CaMgSi2O6 |
Stephenson (1984);
Docka et al. (1986). |
|
Ortopiroxeno-Biotita |
3MgSiO3 + KFe3AlSi3O10(OH)2
=
3FeSiO3 + KMg3AlSi3O10(OH)2 |
Fornarev y Kolnitov (1986); Sengupta
et al. (1990). |
|
Olivino-Espinela |
Mg2SiO4
+ 2FeAl2O4 =
Fe2SiO4
+ 2MgAl2O4 |
Engi (1983). |
|
Cordierita-Espinela |
Mg2Al4Si5O18
+ 2FeAl2O4 =
Fe2Al4Si5O18
+ 2MgAl2O4 |
Vielzeuf (1983). |
|
Olivino-Ortopiroxeno |
Mg2SiO4
+ 2FeSiO3 = Fe2SiO4 + 2MgSiO3 |
Docka et al. (1986); Carswell y Harley
(1990). |
|
Olivino-Clinopiroxeno |
Mg2SiO4
+ 2CaFeSi2O6 =
Fe2SiO4
+ 2CaMgSi2O6 |
Perkins y Vielzeuf
(1992). |
|
Granate-Ilmenita |
Fe3Al2Si3O12
+ 3MnTiO3 =
Mn3Al2Si3O12
+ 3FeTiO3 |
Pownceby et al. (1987a y b). |
|
Ortopiroxeno-Ilmenita |
MgTiO3 +
FeSiO3 = FeTiO3 + MgSiO3 |
Docka et al.
(1986). |
|
Clinopiroxeno-Ilmenita |
MgTiO3 +
CaFeSi2O6 = FeTiO3 + CaMgSi2O6 |
Docka et al.
(1986). |
|
Olivino-Ilmenita |
2MgTiO3
+ Fe2SiO4
= 2FeTiO3 + Mg2SiO4 |
Docka et al.
(1986). |
|
Magnetita-Ilmenita |
Fe3O4
+ FeTiO3 = Fe2TiO4 + Fe2O3 |
Buddington y
Lindsley (1964); Powell y Powell (1977a); Spencer y Lindsley (1981);
Stormer (1983); Andersen (1988); Andersen y Lindsley (1988);
Lindsley et al. (1990); Ghiorso y Sack (1991). |
|
Biotita-Moscovita |
KMg3(AlSi3)O10(OH)2+KAl2(AlSi3)O10(OH)2
= K(Mg2Al)(Al2Si2)O10(OH)2+K(MgAl)Si4O10(OH)2 |
Hoisch (1989). |
|
Plagioclasa-Moscovita |
KAlSi3O8 + NaAl2(AlSi3)O10(OH)2
=
NaAlSi3O8 + KAl2(AlSi3)O10(OH)2 |
Green y Usdansky
(1986). |
|
Plagioclasa-Clinopiroxeno |
NaAlSi3O8
+ CaAl2SiO6 =
CaAl2Si2O8
+ NaAlSi2O6 |
Anovitz (1991). |
|
Plagioclasa-Anfíbol |
NaCa2Mg5AlSi7O22(OH)2
+ NaAlSi3O8 =
Na(NaCa) Mg5Si8O22(OH)2
+ CaAl2Si2O8
NaCa2Mg5AlSi7O22(OH)2
+ 4SiO2 =
Ca2Mg5Si8O22(OH)2
+ NaAlSi3O8
(reacción de
transferencia neta) |
Spear (1980); Blundy y Holland (1990); Holland y Blundy (1994). |
Además de los equilibrios de intercambio
entre dos fases con distintas estructuras, las relaciones de solvus
en sistemas binarios y ternarios también se utilizan con fines
termométricos. La descripción termodinámica de las relaciones de solvus se
presenta en los Temas 3 y 5 del programa propuesto para Petrogénesis
Metamórfica I. Acercamiento Termodinámico, por lo que no se considerará aquí
en detalle. En esencia, el tipo de reacción y las relaciones termodinámicas
son las mismas, aunque los componentes moleculares se mezclan en dos
soluciones sólidas parciales coexistentes, que pueden presentar la misma
estructura (i.e., relaciones de solvus s.s.) o estructuras distintas
(i.e.,
relaciones de laguna composicional). Cuando las estructuras de las
dos fases son idénticas (e.g., en feldespatos ternarios de alta
temperatura), los estados estándar para las dos fases son los mismos, por lo
que sólo existe una única superficie G-X con inflexiones y las ecuaciones se
simplifican: partiendo de la condición de equilibrio entre dos fases,
mia(P,T,X)=mib(P,T,X),
se llega a aia(P,T,X)=aib(P,T,X)
ya que mio,a(P,T)=mio,b(P,T).
Esto no ocurre cuando las estructuras son distintas (e.g., laguna
composicional entre orto y clinopiroxeno), en cuyo caso existe una
superficie G-X, con o sin inflexiones, por cada fase. Los termómetros de
tipo solvus y de tipo laguna composicional más importantes se enumeran en la
Tabla 2.
Tabla 2.- Termómetros solvus y laguna composicional
|
Dos piroxenos |
Distribución de Ca y Mg entre orto y
clinopiroxeno |
Referencias abundates. e.g., Wood y
Banno (1973); Lindsley et al. (1981); Kretz (1982); Lindsley (1983);
Davidson (1985); Davidson y Lindsley (1985). Finnerty y Boyd (1984)
y Carswell y Gibb (1987) discuten gran parte de los calibrados |
|
Calcita-Dolomita |
Distribución de Ca y Mg entre calcita
y dolomita |
Goldsmith y Heard
(1961); Goldsmith y Newton (1969); Gordon y Greenwood (1970);
Walther y Helgeson (1980); Anovitz y Essene (1982, 1987); Powell et
al. (1984). |
|
Dos feldespatos binarios y ternarios |
Distribución de Na y K (±Ca) entre
feldespato alcalino y plagioclasa |
Barth (1962);
Saxena (1973); Stormer (1975); Whitney y Stormer (1977); Powell y
Powell (1977b); Brown y Parsons (1981, 1985); Haselton et al.
(1983); Ghiorso (1984); Green y Usdansky (1986); Fuhrman y Lindsley
(1988); Elkins y Grove (1990). |
|
Moscovita-Paragonita |
Distribución de Na y K entre moscovita
y paragonita |
Eugster et al.
(1972); Chatterjee y Froese (1975); Chatterjee y Flux (1986a y b). |
Por otro lado, los buenos barómetros
deben presentar
bajos incrementos de entalpía y entropía de reacción y fuertes
incrementos de volumen de reacción. Los equilibrios de transferencia neta sólido-sólido (i.e, que no
impliquen componentes de la fase fluida) suelen presentar bajos incrementos
de entalpía y entropía de reacción. Desafortunadamente, la mayor parte de
las reacciones sólido-sólido presentan también incrementos de volumen bajos
debido a la naturaleza condensada de las fases, y por lo tanto son
débilmente dependientes de P. No obstante, existen suficientes equilibrios
que pueden ser utilizados con fines barométricos, como los equilibrios GASP,
ya que presentan incrementos de volumen de reacción suficientes como para
ser dependientes de P, aunque también presentarán una cierta dependencia de
T (i.e., los valores de DHro(P,T)
no se aproximan a 0). Una lista de equilibrios de transferencia neta
calibrados con fines barométricos se presenta en la Tabla 3.
Tabla 3.- Barómetros de transferencia neta.
|
Granate-Plagioclasa-Cuarzo-Silicato de
Al (GASP) |
Ca3Al2Si3O12
+ 2Al2SiO5 + SiO2 =
CaAl2Si2O8 |
Ghent (1976); Ghent
et al. (1979); Newton y Haselton (1981); Hodges y Spear (1982);
Ganguly y Saxena (1984); Hodges y Royden (1984); Lang y Rice (1985);
Powell y Holland (1988); Koziol y Newton (1988); McKenna y Hodges
(1988); Koziol (1989); Koziol y Newton (1989), Berman (1990). |
|
Granate-Cordierita-Silicato de
Al-Cuarzo |
2Mg3Al2Si3O12
+ 4Al2SiO5 + 5SiO2 =
3Mg2Al4Si5O18
(y la reacción en el subsistema de Mg) |
Currie (1971);
Hensen y Green (1973); Weisbrod (1973); Thompson (1976b); Tracy et
al. (1976); Hensen (1977); Holdaway y Lee (1977); Newton y Wood
(1979); Martignole y Sisi (1981); Lonker (1981); Aranovich y
Podlesskii (1983); Bhattacharya y Sen (1985); Mukhopadhyay et al.
(1991). |
|
Ortopiroxeno-Granate-Cordierita-Cuarzo |
2Mg3Al2Si3O12
+ 3SiO2 =
Mg2Al4Si5O18
+ 2Mg2Si2O6 |
Harris y Holland
(1984). |
|
Ortopiroxeno-Silicato de
Al-Cordierita-Cuarzo |
Mg2Si2O6
+ 2Al2SiO5 + SiO2 =
Mg2Al4Si5O18 |
Harris y Holland
(1984). |
|
Granate-Plagioclasa-Moscovita-Biotita |
Ca3Al2Si3O12+Fe3Al2Si3O12+KAl3Si3O10(OH)2
= 3CaAl2Si2O8 + KFe3AlSi3O10(OH)2
(y la reacción en el subsistema de Mg) |
Ghent y Stout
(1981); Hodges y Royden (1984); Hodges y Crowley (1985); Lang y Rice
(1985); Powell y Holland (1988); Hosich (1990, 1991). |
|
Granate-Plagioclasa-Moscovita-Cuarzo |
2Ca3Al2Si3O12
+ Fe3Al2Si3O12 +
3KAl3Si3O10(OH)2
+ 6SiO2 =
6CaAl2Si2O8
+ 3K(FeAl)Si4O10(OH)2
(y la reacción en el subsistema de Mg) |
Hodges y Crowley
(1985); Hosich (1990, 1991). |
|
Granate-Moscovita-Cuarzo-Silicato de
Al |
Fe3Al2Si3O12
+ 3KAl3Si3O10(OH)2
+ 4SiO2 =
4Al2SiO5 + 3K(FeAl)Si4O10(OH)2
(y la reacción en el subsistema de Mg) |
Hodges y Crowley
(1985); Hosich (1991). |
|
Granate-Moscovita-Biotita-Silicato de
Al-Cuarzo |
Fe3Al2Si3O12
+ KAl3Si3O10(OH)2
=
KFe3AlSi3O10(OH)2 +
2Al2SiO5
+ SiO2
(y la reacción en el subsistema de Mg) |
Hodges y Crowley
(1985); Holdaway et al. (1988); Hosich (1991). |
|
Fengita-Feldespato-K-Biotita-Cuarzo |
3K(MgAl)Si4O10(OH)2
=
2KAlSi3O8 + KMg3AlSi3O10(OH)2
+ 3SiO2 + 2H2O |
Velde (1965, 1967);
Powell y Evans (1983); Massone y Schreyer (1987); Bucher-Nurminen
(1987). |
|
Granate-Plagioclasa-Hornblenda-Cuarzo |
3NaAlSi3O8 +
6CaAl2Si2O8
+ 3Ca2(Mg,Fe)5Si8O22(OH)2
=
3NaCa2(Mg,Fe)4Al3Si6O22(OH)2
+ 2Ca3Al2Si3O12 +
(Mg,Fe)3Al2Si3O12
+ 18SiO2
6CaAl2Si2O8
+ 3Ca2(Mg,Fe)5Si8O22(OH)2
=
3Ca2(Mg,Fe)4Al2Si7O22(OH)2
+ 2Ca3Al2Si3O12 +
(Mg,Fe)3Al2Si3O12
+ 5SiO2 |
Kohn y Spear
(1989). |
|
Granate-Plagioclasa-Olivino |
3Fe2SiO4
+ 3CaAl2Si2O8 =
Ca3Al2Si3O12
+ 2Fe3Al2Si3O12 |
Wood (1975); Bohlen
et al., (1983a y c) |
|
Granate-Ortopiroxeno |
Mg3Al2Si3O12
=
Mg2Si2O6 + MgAl2SiO6 |
Carswell y Harley
(1990). |
|
Granate-Plagioclasa-Ortopiroxeno-Cuarzo (GAES y GAFS) |
6MgSiO3 + 3CaAl2Si2O8
=
2Mg3Al2Si3O12 + Ca3Al2Si3O12
+ 3SiO2
(y la reacción en el subsistema de Fe) |
Wood (1975);
Perkins y Newton (1981); Newton y Perlins (1982); Bohlen et al.
(1980, 1983a); Perkins y Chipera (1985); Bhattacharya et al. (1991);
Eckert et al. (1991); Faulhaber y Raith (1991). |
|
Granate-Plagioclasa-Clinopiroxeno-Cuarzo (GADS y GAHS) |
3CaMgSi2O6 +
3CaAl2Si2O8
=
Mg3Al2Si3O12 + 2Ca3Al2Si3O12
+ 3SiO2
(y la reacción en el subsistema de Fe) |
Newton y Perlins
(1982); Perkins (1987); Holland y Powell (1988); Moetecher et al
(1988); Eckert et al. (1991). |
|
Granate-Plagioclasa-Ortopiroxeno-Clinopiroxeno-Cuarzo |
Mg3Al2Si3O12
+ CaMgSi2O6 + SiO2 =
2Mg2Si2O6
+ CaAl2Si2O8
(y la reacción en el subsistema de Fe) |
Paria et al.
(1988). |
|
Plagioclasa-Clinopiroxeno-Cuarzo |
NaAlSi3O8
=
NaAlSi2O6 + SiO2 |
Johannes et al.
(1971); Essene et al. (1972); Hays y Bell (1973); Holland (1980);
Hemingway et al. (1981); Newton (1983); Gasparik (1984); Liou et al.
(1987); Carswell y Harley (1990); Anovitz (1991). |
|
Plagioclasa-Clinopiroxeno-Cuarzo |
CaAl2Si2O8
=
CaAl2SiO6 + SiO2 |
Newton (1983);
Gasparik (1984); Gasparik y Lindsley (1980); Anovitz (1991). |
|
Olivino-Ortopiroxeno-Cuarzo |
2FeSiO3
=
Fe2SiO4 + SiO2 |
Bohlen et al.
(1980); Bohlen y Boetcher (1981); Newton (1983). |
|
Olivino-Granate-Plagioclasa |
Ca3Al2Si3O12
+ 2Mg3Al2Si3O12 =
3CaAl2Si2O8 + 3Mg2SiO4
(y la reacción en el subsistema de Fe) |
Johnson y Essene (1982); Bohlen et al.
(1983); Perkins y Chipera (1985). |
|
Granate-Espinela-Silicato de Al-Cuarzo |
Fe3Al2Si3O12
+ 2Al2SiO5 =
3FeAl2O4
+ 5SiO2 |
Bohlen et al.
(1986). |
|
Granate-Espinela-Silicato de
Al-Corindón |
Fe3Al2Si3O12
+ 5Al2O3 =
3FeAl2O4 +
3Al2SiO5 |
Shulters y Bohlen
(1989). |
|
Granate-Plagioclasa-Rutilo-Ilmenita-Cuarzo (GRIPS) |
Ca3Al2Si3O12
+ 2Fe3Al2Si3O12 + 6TiO2
=
3CaAl2Si2O8 + 3SiO2
+ 6FeTiO3 |
Bohlen y Liotta (1986); Anovitz y
Essene (1987). |
|
Granate-Rutilo-Ilmenita-Silicato de
Al-Cuarzo (GRAIL) |
Fe3Al2Si3O12
+ 3TiO2 =
Al2SiO5 + 2SiO2
+ 3FeTiO3 |
Bohlen el al. (1983b). Ghent y Stout
(1984). |
|
Granate-Esfena-Rutilo-Plagioclasa-Cuarzo |
CaAl2Si2O8
+ 2CaTiSiO5 =
Ca3Al2Si3O12
+ 2TiO2
+ SiO2 |
Ghent y Stout
(1984). |
|
Granate-Esfena-Ilmenita-Cuarzo |
Fe3Al2Si3O12
+ 3CaTiSiO5 =
Ca3Al2Si3O12
+ 3FeTiO3
+ SiO2 |
Essene y Bohlen
(1985). |
|
Granate-Esfena-Magnetita-Plagioclasa-Cuarzo |
4Fe3Al2Si3O12
+ 6CaTiSiO5 =
Ca3Al2Si3O12
+ 3CaAl2Si2O8
+ 6Fe2TiO4 + 9SiO2 |
Essene y Bohlen
(1985). |
|
Granate-Ilmenita-Magnetita-Silicato de
Al-Cuarzo |
Fe3Al2Si3O12
+ 3FeTiO3 =
3Fe2TiO4 + 2SiO2
+ Al2SiO5 |
Bohlen y Liotta
(1986). |
|
Granate-Ilmenita-Magnetita-Plagioclasa-Cuarzo |
Ca3Al2Si3O12
+ 2Fe3Al2Si3O12 + 6FeTiO3
=
6Fe2TiO4 + 3CaAl2Si2O8
+ 3SiO2 |
Bohlen y Liotta
(1986). |
|
Esfena-Distena-Plagioclasa-Rutilo |
CaTiSiO5
+ Al2SiO5
=
CaAl2Si2O8 + TiO2 |
Manning y Bohlen
(1991). |
|
Granate-Wollastonita- Plagioclasa-Cuarzo |
Ca3Al2Si3O12
+ SiO2 =
CaAl2Si2O8 +
2CaSiO3 |
Huckenholz et al.
(1981). |
Notas
Este aspecto se presenta
en el Tema 13 del programa propuesto de Petrogénesis Metamórfica I.
Acercamiento Termodinámico.
Nótese
que de la ecuación (43) no puede inferirse la pendiente de las
rectas tangentes a la curva lnKeq-P
a T constante ya que no se expresa explícitamente la dependencia
respecto de P.
[Back] [Home] [Up] [Next]
Última
modificación:
domingo, 05 de octubre de 2025 15:27 +0200 |