Tutoriales de Evolver | Posgrado Oficial Matemáticas

Tutorial 6

Problemas de frontera libre

Hemos visto cómo hacer que Evolver considere fijo el borde de una superficie, por ejemplo como ocurre en el problema de Plateau. Este caso no es más que uno particular de entre diversos problemas de minimización del área. Los principales tipos son:

Problema de Plateau: Encontrar la(s) superficie(s) de menor área con un borde prefijado. Las soluciones son físicamente películas de jabón, y matemáticamente superficies mínimas (H = 0). Los distintos problemas de Plateau son:
- Con frontera fija: Todas las componentes del borde son curvas prescritas.
- Con frontera libre: Sólo se impone que las componentes del borde sea curvas sobre una o varias superficies "de ligadura" prefijadas. La superficie cortará ortogonalmente a cada superficie de ligadura a lo largo de la frontera libre.
- Mixtos: Cuando algunas componentes del borde están fijas, y las otras son frontera libre.
Problema isoperimétrico: Encontrar la(s) superficie(s) de menor área con un borde prefijado, de entre todas las que encierran un volumen prescrito. Las soluciones son físicamente pompas de jabón, y matemáticamente superficies de curvatura media constante. Este problema tiene las siguentes versiones:
- Sin frontera: Las soluciones son esferas, o pompas dobles, triples, etc.
- Con frontera fija.
- Con frontera libre.
- Mixtos.

Estudiaremos a continuación cómo implementar con Evolver el problema de Plateau con frontera libre. Es este caso nos interesará que uno o varias lados del borde estén contenidos en una superficie prescrita, llamada superficie de ligadura (constraint surface), aunque podrán moverse sobre ella a lo largo del proceso de minimización. La curva (o poligonal) sobre la que la configuración corta a la superficie prescrita se llama curva de contacto, o frontera libre. Para Evolver, la superficies de ligaduras se introducen con el comando constraint, seguido de un número que indica qué superficie de ligadura nos estamos refiriendo, y la ecuación de ésta como superficie de nivel {f = cte} de una función f especificada por el usuario. Por ejemplo:

constraint 1 
formula: z = 0

A la expresión f = cte se le llama ecuación de ligadura. Por ejemplo, "pertenecer al plano horizontal a altura cero" equivale a la ecuación de ligadura z = 0 en el ejemplo anterior. Un vértice puede pertenecer a varias superficies de ligadura, pero el sistema de las ecuaciones de ligadura deben ser no degenerado, es decir, los gradientes de las superficies de ligadura en el punto común deben ser linealmente independientes. En particular, el número de ecuaciones de ligadura no puede exceder el número de dimensiones del espacio ambiente.

Como hemos hecho otras veces, explicaremos cómo implementar problemas de frontera libre mediante un ejemplo práctico: en el fichero free_bdry.fe buscaremos la superficie de área mínima entre aquellas cuyo borde consiste en un cuadrado prescrito y una curva cerrada y simple en el plano {z = 0}. La solución es, de nuevo, una superficie con curvatura media cero:

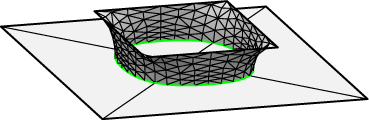
A la vista del gráfico anterior, la topología que prescribimos es la de un cilindro. La configuración inicial será la siguiente:

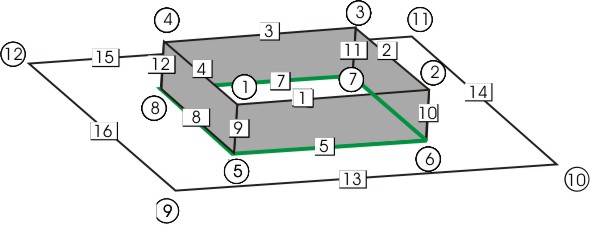
// free_bdry.fe

                    // Illustration of a free boundary on a constraint.

                    // The surface is a ring between a fixed square boundary and

                    // a free boundary on a plane at z = 0.

constraint 1 // the plane Definimos la ligadura
formula: z = 0 La fórmula que define la ligadura ha de ser el conjunto de nivel de una función.

vertices
// the square frame Los vértices (fijos) del cuadrado
1 0 0 0.25 fixed
2 1 0 0.25 fixed
3 1 1 0.25 fixed
4 0 1 0.25 fixed
// the contact line on the plane Los 4 vértices en la curva inicial de frontera libre, a los que imponemos que cumplan la ligadura
5 0 0 0 constraint 1
6 1 0 0 constraint 1
7 1 1 0 constraint 1
8 0 1 0 constraint 1
// for display of the plane Los 4 vértices del plano donde se mueve la frontera libre (fijos)
9 -.5 -.5 0 fixed
10 1.5 -.5 0 fixed
11 1.5 1.5 0 fixed
12 -.5 1.5 0 fixed

edges
// the square frame Los 4 lados (fijos) del cuadrado
1 1 2 fixed
2 2 3 fixed
3 3 4 fixed
4 4 1 fixed
// the contact line Los 4 lados de la curva inicial para la frontera libre (sometidos a la ligadura y en color verde)
5 5 6 constraint 1 color green
6 6 7 constraint 1 color green
7 7 8 constraint 1 color green
8 8 5 constraint 1 color green
// vertical edges to join the two Los 4 lados verticales que unen vértices del cuadrado fijos con los de la frontera libre
9 1 5
10 2 6
11 3 7
12 4 8
// for display of the plane Los lados (fijos) del plano donde se mueve la frontera libre (les impedimos refinarse)
13 9 10 fixed no_refine
14 10 11 fixed no_refine
15 11 12 fixed no_refine
16 12 9 fixed no_refine

faces
// the band of film La película de jabón inicial (i.e. las caras verticales)
1 5 -10 -1 9
2 6 -11 -2 10
3 7 -12 -3 11
4 8 -9 -4 12
// the plane
5 13 14 15 16 fixed no_refine El plano donde se mueve la frontera libre (le impedimos refinarse). 

El resto de órdenes de free_bdry.fe sólo producen una buena convergencia, y no las reproducimos aquí.

Hemos visto cómo la superficie que Evolver muestra, tras evolucionar suficientemente el ejemplo anterior, corta ortogonalmente al plano de ligadura. Esta propiedad es general para todos los problemas de minimización de área con frontera libre:

Si una superficie M es solución de un problema de Plateau con frontera libre respecto a una superficie de ligadura S, entonces M corta a S ortogonalmente.

Cuando la superficie de ligadura S sea un plano, podemos ver la propiedad anterior de ortogonalidad como la condición suficiente para que que al reflejar la superficie en el plano de ligadura, se obtenga una superficie mínima mayor, de la cual ahora el plano de ligadura pasa a ser plano de simetría (principios de reflexión de Schwarz):

Si una superficie mínima M corta ortogonalmente a un plano P, entonces la unión de M con la reflexión de M en P forma una superficie mínima (diferenciable).
Si una superficie mínima M contiene un segmento de recta l, entonces la unión de M con la rotación de 180º de M alrededor de l forma una superficie mínima (diferenciable).

Nota: Podemos usar condiciones de ligadura que no vengan dadas por una ecuación, sino por una desigualdad $f\geq 0$. Esto se usa cuando queremos que elementos de la configuración evolucionen en cierta región, pero si llegan al borde de ésta su comportamiento será el mismo que si la ligadura fuera f = 0. Si el funcional decrece moviendo hacia el interior de $\{ f\geq 0\} $ un elemento que ya estaba en la superficie de ligadura, entonces éste podrá moverse de nuevo libramente. Tenemos un ejemplo en moundpad.fe. (Este ejemplo usa condiciones de capilaridad, por lo que antes estudiaremos la sección siguiente).

Otro ejemplo de problema de frontera libre (mínimo): El problema de Gergonne.

Joseph Diaz Gergonne (1771-1859) fue un militar de renombre en los tiempos que siguieron a la revolución francesa, con múltiples campañas en Francia, Prusia y España. En uno de sus destinos, Nimes, la École Centrale había sido instalada poco antes de su llegada, y fue allí donde Gergonne tomó contacto con las matemáticas (especialmente con Geometría) y abandonó su carrera militar, fuertemente influenciado por el entonces director de la École Polytechnique in Paris, Gaspard Monge. Gergonne tuvo dificultades para publicar sus investigaciones, a lo que dio una curiosa solución: crear su propia revista matemática, Annales de mathématiques pures et appliquées o más conocido por Annales de Gergonne, donde también publicaron matemáticos muy famosos como Poncelet, Steiner, Plücker, Chasles o Galois.

Quizás el resultado más famoso de Gergonne fue su solución al problema de Apolonio, que trata de hallar una circunferencia tangente a tres circunferencias dadas. Lo trascendental de la solución de Gergonne radica en que introduce el concepto de dualidad de la Geometría Proyectiva, según el cual a todo enunciado de geometría proyectiva le corresponde otro donde los subespacios k dimensionales se transforman en sus polares, que son subespacios n-k dimensionales (n es la dimensión ambiente).

Además de probar teoremas, Gergonne propuso muchos problemas que despertaron interés de matemáticos de la época y posteriores. Entre ellos, el que nos proponemos resolver con Evolver: en un cubo se consideran dos diagonales no paralelas, una en su base y la otra en su cara superior.

¿Cuál es la superficie de menor área, contenida en el cubo, cuya frontera consiste en estas dos diagonales junto con curvas libres sobre las caras laterales del cubo?

Llamaremos a este enunciado el problema de Gergonne (propuesto en 1816). Como el ejemplo anterior, éste es un caso particular del llamado problema de Plateau de frontera mixta, en el que se pretende minimizar el área entre todas las superficies que tienen una parte de su frontera prescrita, y el resto de su frontera sólo está obligada a estar contenida en una superficie soporte.

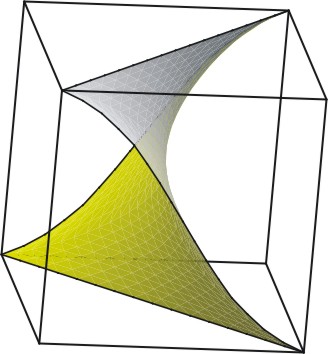
El problema de Gergonne produjo numerosas investigaciones sobre superficie mínimas, e intentos de resolver este problema produjeron otras superficies mínimas famosas, como las debidas a H.F. Scherk en 1835. La solución final del problema de Gergonne se debe a Schwarz, quien usó funciones elípticas para describir la solución. Curiosamente, Schwarz realizó el siguiente grabado en plancha de cobre de la representación gráfica de su solución al problema, un trabajo gráfico que seguro le costó en 1890 muchos más esfuerzos que los que hoy necesitamos para producir un gráfico de la superficie solución con Evolver:

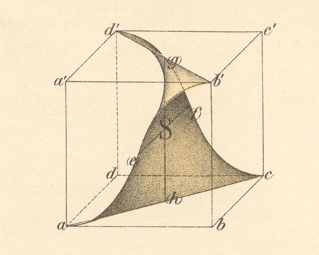
En el gráfico anterior puede verse cómo la superficie de Gergonne S corta a las caras laterales del cubo ortogonalmente (algo general en problemas de Plateau con frontera libre). Usando esto y el principio de reflexión de Schwarz, podemos ver esta superficie como una superficie mínima compacta, bordeada por segmentos de recta (nótese que S contiene dos segmentos ortogonales, uno que une las curvas frontera (e) y (f) y otro que une las curvas frontera (g) y ( h). Si reflejamos el cubo anterior respecto a cada cara y seguimos reflejando respecto de las caras así obtenidas, obtendremos una malla 3D que rellena el espacio mediante copias congruentes del cubo anterior. Si hacemos el mismo proceso de reflexión con S respecto a cada arco de su frontera, obtendremos una superficie infinita, sin borde y sin autointersecciones, que corta a cada cubo de la malla 3D en una copia del gráfico anterior convenientemente reflejada. Esto es lo que se llama una superficie mínima triplemente periódica.

A continuación implementamos la superficie anterior con Evolver. El siguiente gráfico muestra la configuración inicial:

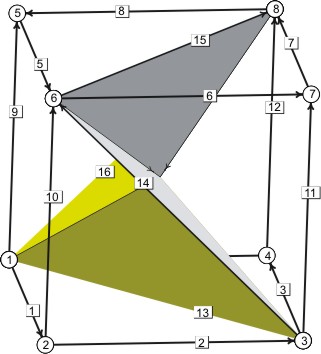
// la superficie de Gergonne

constraint 1
formula: x = 0

constraint 2
formula: x = 1

vertices
// el cubo
1 0.0 0.0 0.0 fixed
2 1.0 0.0 0.0 fixed
3 1.0 1.0 0.0 fixed
4 0.0 1.0 0.0 fixed
5 0.0 0.0 1.0 fixed
6 1.0 0.0 1.0 fixed
7 1.0 1.0 1.0 fixed
8 0.0 1.0 1.0 fixed

edges
//lados del cubo (no intervendrán en el proceso de evolución)
1 1 2 fixed no_refine
2 2 3 fixed no_refine
3 3 4 fixed no_refine
4 4 1 fixed no_refine
5 5 6 fixed no_refine
6 6 7 fixed no_refine
7 7 8 fixed no_refine
8 8 5 fixed no_refine
9 1 5 fixed no_refine
10 2 6 fixed no_refine
11 3 7 fixed no_refine
12 4 8 fixed no_refine

//la superficie (dos lados son fijos, los otros son la frontera libre)
13 1 3 fixed
14 3 6 constraint 2
15 6 8 fixed
16 8 1 constraint 1

faces
1 13 14 15 16 frontcolor yellow

-----------------------------------------

El comando frontcolor sólo puede aplicarse a caras, y se refiere al color del "lado positivo" de una cara. Por defecto, el color asociado es blanco. Para prefijar también el color del "lado negativo" de una cara, usaremos el comando backcolor. Por ejemplo:

Faces 1 1 2 3 frontcolor green backcolor red

El siguiente gráfico muestra cómo Evolver obtiene la misma superficie dibujada por Schwarz:

Un problema isoperimétrico con frontera libre.

A continuación determinaremos la superficie de área mínima de entre todas aquellas superficies S que cumplen:

La frontera de S es un cuadrado C prescrito en el plano z = 0.3.
S toca al plano z=0 y el área del trozo de superficie en el plano z = 0 también se cuenta; esto fuerza a que la superficie de forma diferenciable (es decir, con ángulo 0º) en el plano z = 0.
S junto con el cuadrado C encierran un volumen igual a 1.

El siguiente gráfico muestra la configuración inicial:

// Problema de frontera libre con volumen prescrito

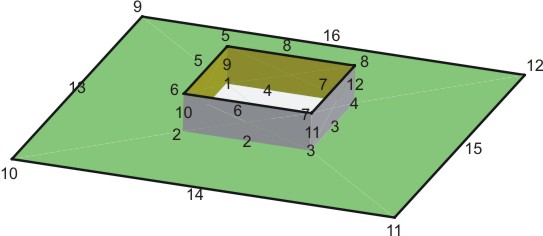
constraint 1
formula: z=0

vertices
1 0.0 0.0 0.0 constraint 1 //los vértices sobre el plano z = 0 (libres, pero sometidos a ligadura)
2 1.0 0.0 0.0 constraint 1
3 1.0 1.0 0.0 constraint 1
4 0.0 1.0 0.0 constraint 1
5 0.0 0.0 0.3 fixed // los vértices fijos (tienen z > 0)
6 1.0 0.0 0.3 fixed
7 1.0 1.0 0.3 fixed
8 0.0 1.0 0.3 fixed
//el plano
9 -1 -1 0 fixed
10 2 -1 0 fixed
11 2 2 0 fixed
12 -1 2 0 fixed

edges
//frontera libre sobre el plano z = 0
1 1 2 constraint 1
2 2 3 constraint 1
3 3 4 constraint 1
4 4 1 constraint 1
//frontera fija, un cuadrado que une los vértices 5,6,7,8
5 5 6 fixed no_refine
6 6 7 fixed no_refine
7 7 8 fixed no_refine
8 8 5 fixed no_refine
// lados móviles en la evolución, uniendo vértices fijos a libres
9 1 5
10 2 6
11 3 7
12 4 8
// lados del plano (auxiliares)
13 9 10 fixed no_refine
14 10 11 fixed no_refine
15 11 12 fixed no_refine
16 12 9 fixed no_refine

faces
1 1 10 -5 -9 backcolor yellow
2 2 11 -6 -10 backcolor yellow
3 3 12 -7 -11 backcolor yellow
4 4 9 -8 -12 backcolor yellow
5 5 6 7 8 color clear no_refine fixed // Esta cara se define para luego poder definir una región (body) y así imponer un volumen. Se deja transparente.
6 -4 -3 -2 -1 constraint 1 no_refine
//el plano
7 13 14 15 16 color lightgreen no_refine fixed

bodies
1 1 2 3 4 5 6 volume 1

Tras evolucionar el fichero anterior, llegamos al gráfico

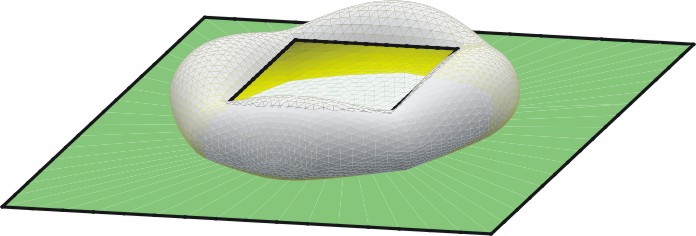
Ángulo de contacto y capilaridad

Hay circunstancias en las que un líquido moja una superficie sólida S, pero cuando la superficie M del líquido corta a S no lo hace en ángulo recto, sino con un cierto ángulo prescrito. Este ángulo de denomina ángulo de contacto, y el fenómeno, capilaridad. Hemos visto un ejemplo de esto en los problemas de frontera libre, donde el ángulo de contacto es 90º. Otras situaciones físicas en los que aparecen fenómenos de capilaridad con ángulos de contacto no necesariamente rectos, son el menisco del vino en una copa de cristal, o el de gotas de líquido sobre una superficie lisa S. En este último caso, podemos observar distintos ángulos de contacto dependiendo del líquido empleado:

Cuando el líquido moja la superficie S, el ángulo de contacto medido desde el interior del líquido es menor de 90º, como ocurre en el ejemplo de la izquierda anterior. Si el líquido y la superficie se repelen, como en el ejemplo de la derecha, el ángulo de contacto es mayor de 90º. A continuación tenemos gráficos de gotas hechos con Evolver, donde el ángulo de contacto es 60º, 90º y 120º:

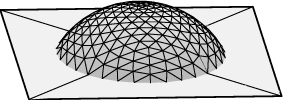
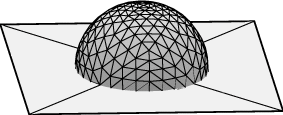
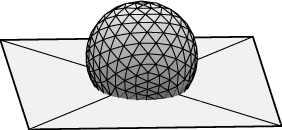
Desde un punto de vista teórico, la capilaridad es un fenómeno que se modela mediante los puntos críticos de un funcional distinto del área:

Sea $\Sigma\subset\mathbb{R}^3$ una superficie. Consideremos la familia de superficies \[\mathcal{M}=\{M\subset\mathbb{R}^3 \text{ superficie}: \partial M\subset \Sigma \}\] Supongamos que cada $M\in\mathcal{M}$ bordea un subdominio compacto $D\subset\Sigma$. Dado $c\in\mathbb{R}$, consideramos el funcional \[M\in\mathcal{M}\mapsto E_c(M)=\mbox{Area}(M)+c\mbox{ Area}(D).\] De la primera fórmula de variación de $E_c$ se obtiene:

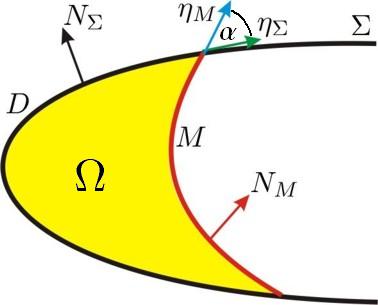
$M$ es punto crítico de $E_c$ para toda variación de $M$ en $\mathcal{M}$ si y sólo la curvatura media de $M$ es idénticamente nula y $M$ corta a $\Sigma$ con ángulo constante $\alpha$ definido por $c=\cos(\alpha)$.
$M$ is punto crítico de $E_c$ para toda variación de $M$ en $\mathcal{M}$ que preserva el volumen si y sólo si curvatura media de $M$ es constante y $M$ corta a $\Sigma$ con ángulo constante $\alpha$ definido por $c=\cos(\alpha)$.

Nótese que en el primer punto anterior se trata el Problema de Plateau con capilaridad, y el segundo explica el problema isoperimétrico con capilaridad.

El funcional $E_c$ se reduce al área para $c=0$, es decir, para problemas de frontera libre. Pero si queremos estudiar un caso de capilaridad con ángulo distinto de 90º, tendremos que tomar el funcional $E_c$ adecuado en términos del ángulo de contacto. A continuación veremos cómo implementar estos problemas de capilaridad con Evolver. Hay dos formas de hacer esto, en función de si la superficie de ligadura ($\Sigma$ en el desarrollo teórico anterior) es un trozo de plano o no. El método para implementar problemas de capilaridad con $\Sigma$ no plana es más general, y puede usarse también para los casos $\Sigma$ plana, pero es más complicado que el método específico para $\Sigma$ plana.

En ambos métodos y como ocurría en el caso de frontera libre, la superficie de ligadura $\{ f=0 \}$ se representa en Evolver mediante los comandos

constraint x 
formula: f=0

donde x es el número correspondiente a la ligadura (puede ponerse f=cte para una constante que no sea cero). En el caso de que el ángulo de contacto sea distinto de 90º, debemos dar un dato más a Evolver relacionado con la ligadura: el ángulo de contacto (en otras palabras, si no damos el ángulo de contacto Evolver entenderá que éste es de 90º y tendremos un problema de frontera libre). Sin embargo, el ángulo de contacto no se da directamente. En su lugar, se dan la TENSION o un campo de vectores que contiene la información de la tensión y algo más (éste último caso si $\Sigma$ no es plana). Para entender esto, primero debemos conocer el concepto de tensión superficial en Evolver.

Dada una superficie $D$, la tensión superficial de $D$ (surface tension) es un número real $T$. La energía superficial de $D$ es

\[\text{Energía superficial}(D) = T\cdot\mbox{Area}(D).\]

En seguida veremos que en el desarrollo teórico anterior, la tensión de $D$ es $T=\cos(\alpha)$. Por defecto, la tensión para Evolver es 0 (es decir, $\alpha =90^o$) y la energía superficial coincide con el área (problema de frontera libre). Podemos asignar a una cara (o unión de caras) una tensión, usando el comando tension (ver el ejemplo moundfull.fe más abajo). ¿Cómo podemos usar la tensión superficial con los problemas de capilaridad?

Sea $M\in {\cal M}$ un punto crítico de $E_c$ con $c=\cos (\alpha )$ y $\alpha \in \mathbb{R} $ dado. Entonces, \[E_c(M)=\mbox{Area}(M)+\mbox{Energía superficial}(D),\] donde estamos considerando en $D$ la tensión superficial $c$. Por tanto, podemos indicar a Evolver el ángulo de contacto $\alpha $ por medio de la Energía superficial. Pero ésta es (salvo la constante $c$) el área de $D$, que conlleva cálculos a lo largo de la superficie de ligadura $\Sigma $. Sin embargo, por medio del Teorema de Stokes podremos reducir estos cálculos a una integral de línea sobre $\partial M$:

Denotaremos por $N_M,N_{\Sigma }$ a los normales unitarios a $M$ y $\Sigma$ que apuntan al exterior de la región $\Omega $ encerrada por $M$ y $\Sigma $ (ver gráfico arriba). Supongamos que existe un campo diferenciable $X$ sobre un abierto simplemente conexo $\Omega'\subset\mathbb{R}^3$ que contiene a $\Omega $, tal que $X=N_{\Sigma }$ a lo largo de $\Sigma $. Entonces,

\[\mbox{Area}(D)=\int _DdA_{\Sigma }=\int _D\langle X,N_{\Sigma }\rangle dA_{\Sigma },\] donde $dA_{\Sigma }$ es el elemento de área sobre $\Sigma $. Si además suponemos que la divergencia (euclídea) de $X$ es cero, entonces $d(i(X)dV)=\mbox{div}(X)dV=0$ (aquí $i(X)dV$ es el producto interior de $X$ con el elemento de volumen en $\mathbb{R}^3$, y $d$ es la diferencial exterior). Así, $i(X)dV$ es una 2-forma cerrada en el simplemente conexo $\Omega '$. Por tanto, $\exists W$ campo diferenciable sobre $\Omega '$ tal que \[\mbox{rotacional}(W)=d(W^{\flat })=i(X)dV \quad \mbox{en }\Omega'.\] Por tanto, \[\mbox{Area}(D)=\int _Di(X)dV=\int _Dd(W^\flat )=\int _{\partial D}W^{\flat }=-\int _{\partial M}W^{\flat }.\] Lo anterior nos dice cómo podemos calcular el área de $D$ a partir del dato $W$, haciendo cálculos sólo sobre la frontera de M. Esto es especialmente interesante para Evolver, porque la superficie a evolucionar es $M$, pero no $\Sigma$. Análogamente, podemos calcular la energía superficial de $D$ con el ángulo de contacto y el campo $-W$ como una integral de línea sobre el borde de $M$: \[\text{Energía superficial}(D)=\cos(\alpha)\int_{\partial M}(-W)^\flat.\]

En la práctica, para implementar un problema de capilaridad con ángulo alfa distinto de 90º daremos una de las dos siguientes parejas de datos:

La superficie de ligadura y la tensión superficial de $D$.
La superficie de ligadura y el campo $E=-\cos(\alpha) W$ (que incluye el dato de tensión superficial $-\cos(\alpha)$).

La segunda opción anterior es obligatoria si la superficie de ligadura no es plana, pero el campo $E$ hay que indicárselo a Evolver dando sus tres componentes como campo en $\mathbb{R}^3$ (coordenadas cartesianas). Esto pasa por calcular las coordenadas del campo $W$, y para ello debemos resolver dos problemas previos:

Encontrar un campo $X$ definido en $\Omega'$, que tenga divergencia euclídea cero y que sobre $\Sigma$ coincida con $N_\Sigma$.
Encontrar un campo $W$ definido en $\Omega'$, que cumpla $d(W^\flat)=i(X)dV$.

(Si se siguen las cuentas anteriores, veremos que no hace falta que $\Omega'$ sea simplemente conexo, basta que existan $X$ y $W$).

Como siempre, explicaremos esto con ejemplos, uno donde la superficie de ligadura es llana y otro donde no lo es. Usaremos el fichero moundfull.fe (mound = montículo), que producirá los tres gráficos de gotas anteriores. La superficie inicial será un cubo unitario con una base apoyada en el plano z = 0, que es la superficie de ligadura, y resolveremos un problema isoperimétrico (esto es, prescribimos un volumen y minimizamos área) con codiciones de capilaridad de distintos ángulos.

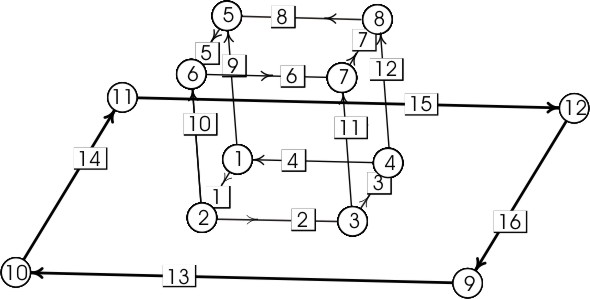
La cara inferior del cubo, así como sus 4 vértices y sus 4 lados, están sometidos a la ligadura 1 (luego tras refinar seguirán cumpliéndola). Como vimos arriba, la energía superficial de la base del cubo es $\cos(\alpha)$ por el área de la base del cubo, es decir, $\cos(\alpha)$. Si queremos que el ángulo de capilaridad a sea recto, simplemente impondremos que la tensión superficial de la cara que representa la interfase líquido-sólido (la base del cubo) se anule.

// moundfull.fe
// Evolver data for drop of prescribed volume sitting on plane with gravity. 
// Body is fully surrounded by facets. Este comentario se refiere a que podria implementarse de forma distinta, sin definir la base del cubo (veremos esto más abajo). 
// Contact angle with plane can be varied by changing tension of contact facets.
gravity_constant 0 // start with gravity off
constraint 1 /* the table top */ La ligadura es el plano z = 0
formula: z = 0

vertices
1 0.0 0.0 0.0 constraint 1 /* 4 vertices on plane */ Los vértices interiores del cubo 1,2,3,4 están sometidos a la ligadura 1
2 1.0 0.0 0.0 constraint 1
3 1.0 1.0 0.0 constraint 1
4 0.0 1.0 0.0 constraint 1
5 0.0 0.0 1.0 Los vértices superiores del cubo 5,6,7,8 son libres.
6 1.0 0.0 1.0
7 1.0 1.0 1.0
8 0.0 1.0 1.0
9 2.0 2.0 0.0 fixed /* for table top */ Los vértices 9,10,11,12 definen el tablero sobre el que estará la gota. Son fijos.
10 2.0 -1.0 0.0 fixed
11 -1.0 -1.0 0.0 fixed
12 -1.0 2.0 0.0 fixed

edges /* given by endpoints and attribute */

1 1 2 constraint 1 /* 4 edges on plane */ Los lados 1,2,3,4 son los inferiores del cubo, y están sometidos a la ligadura 1
2 2 3 constraint 1
3 3 4 constraint 1
4 4 1 constraint 1
5 5 6 Los 8 lados restantes del cubo son libres.
6 6 7
7 7 8
8 8 5
9 1 5
10 2 6
11 3 7
12 4 8

13 9 10 no_refine fixed /* for table top */ Los lados 13,14,15,16 corresponden a los lados del tablero. No deben refinarse y son fijos.
14 10 11 no_refine fixed
15 11 12 no_refine fixed
16 12 9 no_refine fixed

faces /* given by oriented edge loop */

1 1 10 -5 -9 Las caras 1,2,3,4,5 son las caras del cubo distintas de la base. Son libres al refinar e iterar.
2 2 11 -6 -10
3 3 12 -7 -11
4 4 9 -8 -12
5 5 6 7 8

6 -4 -3 -2 -1 color green constraint 1 tension 0 Esta es la base del cubo, con su orientación exterior. Ha sido coloreada en verde, está sujeta a la ligadura 1 y se ha impuesto que el ángulo de contacto sea 90º, mediante la condición "tension 0".

7 13 14 15 16 no_refine density 0 fixed /* table top for display */ Esta es la cara del tablero. Es fija, no refinable. El atributo "density" es, en este caso, sinónimo de tensión (density para objetos 1D representa tensión lineal, y para objetos 3D, es la densidad gravitacional).

bodies /* one body, defined by its oriented faces */

1 1 2 3 4 5 6 volume 1 density 1 Hay un sólo cuerpo, el interior del cubo. Le asignamos volumen fijo 1, y densidad de gravedad 1.

(tras probar con otros valores de density para la cara 7 y para el cuerpo 1, los resultados son aparentemente iguales). Si ahora queremos variar el ángulo de contacto de alfa = 90º a alfa = 60º, podemos redefinir la cara nº 6 o alternativamente usar de nuevo que la energía superficial de la base del cubo es $-\cos(\alpha)=-\cos 60$º$=-0.5$. (el signo menos sale por cuestiones de orientación, como el cambio de signo en la integral de arriba a lo largo de los bordes de $D$ o de $M$). Ahora sólo tenemos que teclear

set facet tension -0.5 where on_constraint 1

y refinar-iterar. Análogamente, para imponer un ángulo de contacto de 120º teclearemos

set facet tension 0.5 where on_constraint 1

y refinar-iterar.

Problemas de capilaridad cuando la superficie de ligadura no es plana.

A continuación aprenderemos a usar Evolver para modelar el fenómeno de capilaridad que se produce cuando observamos el menisco del vino en una copa de cristal, o el del agua en un tubo de cristal:

Este tipo de fenómenos es muy estudiado actualmente, por ejemplo para diseñar contenedores de líquidos en una nave espacial, en ausencia de gravedad o en gravedad muy baja. La tensión de la superficie del líquido, que depende de la gravedad, determinará la forma de dicha superficie. Si no queremos que el líquido se escape del contenedor, deberemos estudiar la forma de la superficie.

El fichero que usaremos para mostrar cómo implementar esta situación con Evolver es capillary.fe, donde la superficie de ligadura es un cilindro vertical, sin tener en cuenta la acción de la gravedad. Como la superficie de ligadura no es plana, debemos usar el segundo método de los citados arriba para prescribir un ángulo de contacto (daremos la superficie de ligadura y el campo $E=-\cos(\alpha) W$).

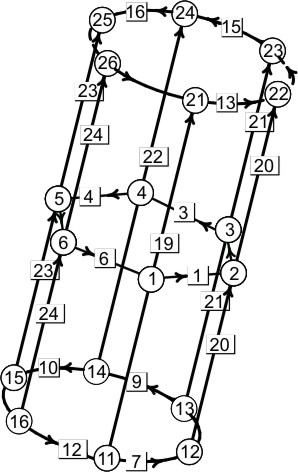
// capillary.fe

// Demonstration of curved constraint - capillary meniscus in 
// vertical tube.

parameter radius = 1 // of tube Definimos 3 parámetros: radio del cilindro (1),...
parameter height = 4 // of tube ..., altura del cilindro (4), y...
parameter angle = 45 // interior contact angle, degrees ... ángulo de contacto (45º).

#define WALLT (-cos(angle*pi/180)) definimos WALLT (=wall tension), que es -cos(alfa).
constraint 1 // the tube wall, for contact line definimos la ligadura 1: el cilindro.
formula: x^2 + y^2 = radius^2
energy: 
e1: -WALLT*z*y/radius Componentes del campo E=-cos(alfa) W.
e2: WALLT*z*x/radius
e3: 0

Veamos esto último con más detalle antes de seguir. El campo normal exterior a la superficie de ligadura es \[N_\Sigma=\frac{1}{R}(x,y,0).\] Por otro lado, el campo de vectores \[X=\frac{R}{x^2+y^2}(x,y,0)\] tiene divergencia euclídea cero (no está definido en un simplemente conexo) y coincide con $N_\Sigma$ sobre $\Sigma$. Y el campo \[W=\frac{Rz}{x^2+y^2}(y,-x,0)\] cumple $d(W^\flat)=i(X)dV$. Como la integral a la que se reduce la energía superficial de $D$ era \[\text{Energía superficial}(D)=\cos(\alpha)\int_{\partial M}(-W)^\flat,\] en nuestro caso el campo $E$ sobre el borde de $M$, del cual Evolver debe calcular la integral de línea a lo largo del borde de $M$, es \[E=-\cos(\alpha)(W_{|\partial M})=-\frac{z}{R}\cos(\alpha)(y,-x,0).\] que son las componentes que podemos leer arriba. Seguimos con el análisis del fichero capillary.fe:

constraint 2 // the tube wall, for display La ligadura 2 también es el cilindro, pero ahora sin asociarle ángulo de contacto.
formula: x^2 + y^2 = radius^2 Usaremos la ligadura 2 para definir el gráfico que mostrará el cilindro 

vertices
// the meniscus
1 radius*cos(0*pi/3) radius*sin(0*pi/3) height/2 constraint 1 Los vértices de la curva de contacto, a mitad de altura y sometidos a la ligadura 1
2 radius*cos(1*pi/3) radius*sin(1*pi/3) height/2 constraint 1
3 radius*cos(2*pi/3) radius*sin(2*pi/3) height/2 constraint 1
4 radius*cos(3*pi/3) radius*sin(3*pi/3) height/2 constraint 1
5 radius*cos(4*pi/3) radius*sin(4*pi/3) height/2 constraint 1
6 radius*cos(5*pi/3) radius*sin(5*pi/3) height/2 constraint 1
// bottom of tube
11 radius*cos(0*pi/3) radius*sin(0*pi/3) 0 constraint 2 Los vértices de la circunferencia inferior del cilindro (altura 0), sometidos a la ligadura 2
12 radius*cos(1*pi/3) radius*sin(1*pi/3) 0 constraint 2
13 radius*cos(2*pi/3) radius*sin(2*pi/3) 0 constraint 2
14 radius*cos(3*pi/3) radius*sin(3*pi/3) 0 constraint 2
15 radius*cos(4*pi/3) radius*sin(4*pi/3) 0 constraint 2
16 radius*cos(5*pi/3) radius*sin(5*pi/3) 0 constraint 2
// top of tube
21 radius*cos(0*pi/3) radius*sin(0*pi/3) height constraint 2 Los vértices de la circunferencia superior del cilindro (altura 4), sometidos a la ligadura 2
22 radius*cos(1*pi/3) radius*sin(1*pi/3) height constraint 2
23 radius*cos(2*pi/3) radius*sin(2*pi/3) height constraint 2
24 radius*cos(3*pi/3) radius*sin(3*pi/3) height constraint 2
25 radius*cos(4*pi/3) radius*sin(4*pi/3) height constraint 2
26 radius*cos(5*pi/3) radius*sin(5*pi/3) height constraint 2

edges 
// the meniscus
1 1 2 constraint 1 Los lados de la curva de contacto, sometidos a la ligadura 1
2 2 3 constraint 1
3 3 4 constraint 1
4 4 5 constraint 1
5 5 6 constraint 1
6 6 1 constraint 1
// the bottom of the tube
7 11 12 constraint 2 fixed bare no_refine Los lados de la base del cilindro. Son fijos, no refinables.
8 12 13 constraint 2 fixed bare no_refine El atributo "bare" (=al descubierto") se usa para indicar a Evolver que el lado no está asociado a una cara (representaremos sólo el "esqueleto" del cilindro)
9 13 14 constraint 2 fixed bare no_refine
10 14 15 constraint 2 fixed bare no_refine
11 15 16 constraint 2 fixed bare no_refine
12 16 11 constraint 2 fixed bare no_refine
// top of the tube
13 21 22 constraint 2 fixed bare no_refine Los lados de la tapa del cilindro. Son fijos, no refinables. 
14 22 23 constraint 2 fixed bare no_refine
15 23 24 constraint 2 fixed bare no_refine
16 24 25 constraint 2 fixed bare no_refine
17 25 26 constraint 2 fixed bare no_refine
18 26 21 constraint 2 fixed bare no_refine
// Verticals sides of tube Los lados verticales del cilindro (generatrices). Son fijos, no refinables.
19 11 21 constraint 2 fixed bare no_refine 
20 12 22 constraint 2 fixed bare no_refine
21 13 23 constraint 2 fixed bare no_refine
22 14 24 constraint 2 fixed bare no_refine
23 15 25 constraint 2 fixed bare no_refine
24 16 26 constraint 2 fixed bare no_refine

faces
1 1 2 3 4 5 6 Sólo hay una cara, el disco horizontal a altura intermedia en el cilindro.

bodies 
1 1 volume pi*radius^2*height/2 Sólo hay un cuerpo, el determinado por el cilindro desde su base hasta la cara 1. Imponemos que su volumen sea fijo (en función del radio y altura).

read

// get top and bottom round-looking Estas lineas refinan los lados correspondientes a la base y tapa del cilindro, incluso antes de empezar a iterar para resolver el problema de capilaridad. De esta forma, la base y tapa son circulares desde el principio. 
refine edge where original >= 7 and original <= 18
refine edge where original >= 7 and original <= 18
refine edge where original >= 7 and original <= 18

Ejercicios

1. Resolver mediante Evolver los problemas de tipo mixto asociados a los contornos siguientes, donde trazo continuo significa frontera fija y trazo discontinuo corresponde a frontera libre en una cara vertical.

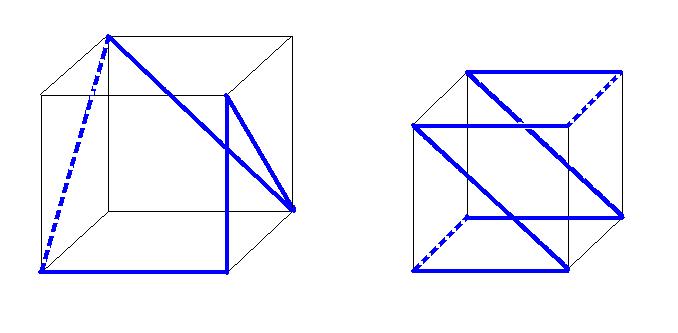
2. Crear dos ficheros gotaA.fe y gotaB.fe para implementar una gota de líquido situada en la esquina que forman un plano horizontal (suelo) y un plano vertical (pared), de foma que el ángulo de contacto es de 110º con la pared y de 60º con el suelo, como en la figura siguiente: gota

En gotaA.fe, la gota tendrá todas sus caras. En gotaB.fe, sustituiremos las caras llanas de la gota (es decir, las caras de la gota sobre el suelo y sobre la pared) por condiciones integrales sobre el borde de las caras de la gota adyacentes.

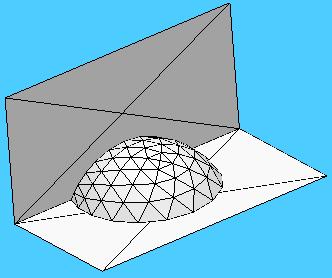
3. Crear un fichero marco.fe para implementar un marco cúbico fijo, sobre el se tiende una película de jabón que tiene un cuadrado "redondeado" en su centro, como en la siguiente figura:

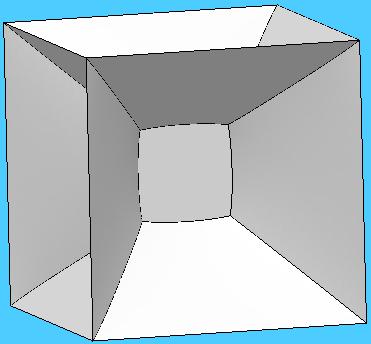Indicación: Partir de una superficie inicial que tenga un marco cúbico encerrando un cuadrado "recto" en su centro. La configuración tendrá:
- Vértices: las 8 esquinas del cubo exterior (fijas), y las cuatro esquinas del cuadrado interior (no fijos).
- Aristas: 12 aristas fijas del cubo exterior, 4 aristas no fijas del cuadrado interior, y 8 aristas no fijas que unan las esquinas del cubo con las esquinas del cuadrado interior.
- Caras: 1 cuadrado central, 4 triángulos y 8 cuadriláteros.

Formas y curvatura: Surface Evolver