Tutorial 4
Problemas de frontera fija. El problema de Plateau
A continuación aprenderemos a prefijar parte de la configuración inicial en el proceso de minimización. El ejemplo que usaremos, contenido en el fichero cat.fe, produce un trozo compacto de la catenoide. La energía a minimizar es de nuevo el área, pero ahora no prescribimos volumen. Usando la fórmula de variación del área que obtuvimos en el tutorial 2,
lo anterior debe anularse para toda función diferenciable u sobre M, con soporte compacto. Esto nos lleva a H=0, es decir, M es una superficie mínima.
El primer ejemplo de superficie mínima es el plano. Si buscamos superficies mínimas de revolución, sólo obtendremos otro ejemplo: la catenoide. La catenoide es la superficie obtenida rotando alrededor del eje z la curva llamada catenaria, de ecuación
donde a es un parámetro positivo que controla la escala. La catenoide es una superficie completa e ilimitada, aunque aquí sólo vemos un trozo compacto de la misma:
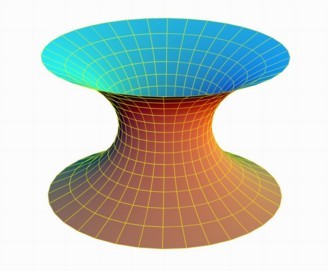
En general, el problema de Plateau persigue encontrar la(s) superficie(s) de menor área de entre todas las que tienen un borde prescrito. En nuestro caso, la frontera que prescribiremos consiste en dos circunferencias, que daremos a Evolver mediante parametrizaciones.
Prefijamos un radio (por ejemplo, común a ambas circunferencias e igual a RMAX=1.5088795) y una altura para cada una de ellas ZMAX=1, -ZMAX=-1. Indicamos a Evolver que la frontera de la superficie consiste en dos partes (boundary 1,2) dadas por una curva parametrizada cada una (parameters 1). Tras definir las parametrizaciones, Evolver entiende que las fronteras están prescritas y no sujetas al proceso de evolución.
// cat.fe
// Evolver data for catenoid.
PARAMETER RMAX = 1.5088795 // minimum radius for height
PARAMETER ZMAX = 1.0
boundary 1 parameters 1 // upper ring
x1: RMAX * cos(p1)
x2: RMAX * sin(p1)
x3: ZMAX
boundary 2 parameters 1 // lower ring
x1: RMAX * cos(p1)
x2: RMAX * sin(p1)
x3: -ZMAX
Nótese que tras boundary n paraterers 1, hemos listado las componentes (x1,x2,x3) de una parametrización de cada curva frontera. RMAX y ZMAX son parámetros, que pueden cambiarse mediante el comando
A
(en mayúsculas), que produce una lista con los parámetros y sus valores actuales, asignando a cada una de ellas un dígito. Para cambiar el valor asignado a un parámetro, teclearemos el dígito asociado y a continuación el nuevo valor del parámetro. Saldremos del comando A pulsando ENTER tras una línea en blanco. Cuando definamos una frontera 1D, su parámetro será siempre p1. Si la frontera es 2D, usaremos p1, p2 como parámetros. Nótese que Evolver entiende parametrizaciones periódicas, como en este ejemplo.
Tal y como hemos visto en el gráfico de arriba, la catenoide tiene la topología de un cilindro. Por tanto, ésta será también la topología de la superficie inicial, que consiste en 6 rectángulos formando un cilindro con vértices sobre las dos circunferencias frontera.
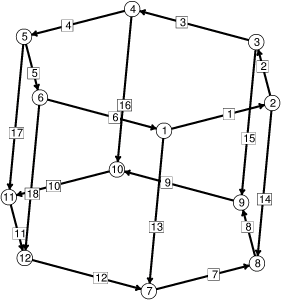
En lugar de dar las tres coordenadas de cada vértice (que es lo que hicimos en el tutorial 2), indicamos el valor del parámetro (p1) que lo produce sobre las circunferencias frontera. También indicamos que los vértices están sujetos a la frontera (mediante el atributo fixed). Cuando asignamos este atributo a un objeto, le estamos obligando a permanecer fijo en el proceso de evolución. También asociaremos el atributo fixed a los lados que unan pares de vértices frontera. Esto hace que cuando refinemos un lado que una dos vértices en la frontera, Evolver introduzca un vértice nuevo (situado en el punto medio del segmento), vértice que también será fijo en las iteraciones.
vertices // given in terms of boundary parameter
1 0.00 boundary 1 fixed
2 pi/3 boundary 1 fixed
3 2*pi/3 boundary 1 fixed
4 pi boundary 1 fixed
5 4*pi/3 boundary 1 fixed
6 5*pi/3 boundary 1 fixed
7 0.00 boundary 2 fixed
8 pi/3 boundary 2 fixed
9 2*pi/3 boundary 2 fixed
10 pi boundary 2 fixed
11 4*pi/3 boundary 2 fixed
12 5*pi/3 boundary 2 fixed
edges
1 1 2 boundary 1 fixed
2 2 3 boundary 1 fixed
3 3 4 boundary 1 fixed
4 4 5 boundary 1 fixed
5 5 6 boundary 1 fixed
6 6 1 boundary 1 fixed
7 7 8 boundary 2 fixed
8 8 9 boundary 2 fixed
9 9 10 boundary 2 fixed
10 10 11 boundary 2 fixed
11 11 12 boundary 2 fixed
12 12 7 boundary 2 fixed
13 1 7 A continuación, los lados que no son fijos. 14 2 8 15 3 9 16 4 10 17 5 11 18 6 12 faces 1 1 14 -7 -13 2 2 15 -8 -14 3 3 16 -9 -15 4 4 17 -10 -16 5 5 18 -11 -17 6 6 13 -12 -18
Como dijimos arriba, si especificamos la opción fixed para un lado, entonces todos los vértices que puedan producirse por refinamientos en ese lado también serán fijos. Esto se extiende a lados y caras.
Si tecleamos g n (n=número) en este caso, no obtendremos evolución alguna. Debemos entonces refinar la triangulación. Pero si no vamos con cuidado, podemos obtener resultados muy lejos del resultado deseado. Veamos un ejemplo (ojo: lo que sigue depende de la versión de Evolver; se adjuntan dos posibilidades para llegar a una singularidad y luego eliminar el vértice singular; probar ambas):
- Primera opción. Tecleamos la secuencia:
- r (refina la triangulación: los lados se dividen en 2, las caras en 4 y se heredan los atributos; Evolver responde dando el número de elementos estructurales y cantidad de memoria consumida por la nueva configuración)
- u (uniformiza la triangulación - "equiangulation")
- g 120 (hace 120 iteraciones, lo que hace que el cuello evolucione a una singularidad)
- t 0.05 (elimina lados muy pequeños y las caras adyacentes; el parámetro 0.05 indica que los lados menores que este valor se eliminarán)
- o (divide el vértice "singular" sustituyéndolo por dos esferas, con lo que la superficie se separa en dos componentes)
- g (hace una iteración más, en este caso separando aún más ambas componentes)
- Segunda opción. Tecleamos la secuencia:
- r (refina la triangulación: los lados se dividen en 2, las caras en 4 y se heredan los atributos; Evolver responde dando el número de elementos estructurales y cantidad de memoria consumida por la nueva configuración)
- u (uniformiza la triangulación - "equiangulation")
- g 92 (hace 92 iteraciones, en la última hemos obtenido scale 0 luego no evolucionaremos más sin modificar la combinatoria de la configuración)
- t 0.05 (elimina lados muy pequeños y las caras adyacentes; el parámetro 0.05 indica que los lados menores que este valor se eliminarán, es este caso 12 lados)
- g 30 (hace 30 iteraciones, creando una singularidad)
- t 0.05 (elimina 12 lados)
- o (divide el vértice "singular" sustituyéndolo por dos esferas, con lo que la superficie se separa en dos componentes)
- g (hace una iteración más, en este caso separando aún más ambas componentes)
En ambos casos, hemos cambiado la topología inicial, al aplicar el comando o.
Habitualmente, una combinación de "refinamiento-iteración" produce una buena convergencia a un mínimo local de la energía (i.e. del área). Una forma de acelerar el proceso de convergencia es cambiando el algoritmo usado en la evolución, con el comando U, que cambia el algoritmo por defecto, llamado de Fletcher-Reeves.
Para ver otros comandos útiles en el proceso de iteraciones, teclear (en modo de comandos) h.
Ejercicios
1. Resolver con Evolver el problema de Plateau en cada uno de los siguientes cinco contornos, cuyos vértices son vértices de un cubo:
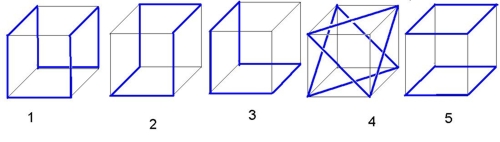
2. Construir el anillo mínimo para el contorno 5 del ejercicio anterior, definiendo la altura como parámetro. Encontrar aproximadamente, mediante distintos ensayos con Evolver, el valor crítico de la altura para la existencia del anillo mínimo.
3. Consideremos la hélice $h(t)=(\cos(t),\mbox{sen}(t),t)$. Crear un fichero helicoide.fe para resolver un problema de Plateau sobre la curva de Jordan obtenida al unir el arco de esta hélice entra las alturas $0$ y $2\pi$ con el segmento del eje z entre esas alturas, por medio de segmentos rectilíneos contenidos en los planos $\{z=0\}$ y $\{z=2\pi \}$.
4. Crear un fichero Mobius.fe para resolver un problema de Plateau sobre una curva de Jordan que produzca una superficie mínima no orientable (por ejemplo, una cinta de Möebius).