Formas y curvatura: Surface Evolver

Posgrado Oficial Matemáticas - Universidad de Granada

Tutorial 8

Optimización de otras energías

Además del área (o tensión superficial) para superficies y la longitud para curvas, existen otras cantidades importantes a la hora de modelar diversos procesos geométricos y físicos de optimización. Por ejemplo, en Geometría podemos citar las "energías de curvatura" (bending energies), cuyos puntos críticos son las curvas elásticas en el caso 1D y las superficies de Willmore en el caso 2D. También tienen cabidas otras energías más útiles en Física, como la gravitatoria. Las cantidades definidas por el usuario a las que intentaremos aplicar Evolver deberán cumplir una serie de requisitos:

  1. Serán globales, es decir modelarán integrales sobre una curva o superficie (en realidad, sobre lados y caras de una configuración de las que Evolver maneja). Si queremos modelar una integral sobre un recinto 3D, usaremos el Teorema de la divergencia para escribirla como integral 2D.
  2. Deben depender sólo de las variables en la configuración inicial, es decir, deben ser evaluables a partir de vértices, aristas, caras y cuerpos.
  3. Pueden referirse no sólo al funcional cuyos puntos críticos estamos buscando (área), sino a magnitudes que queremos que permanezcan fijas (p.e. volumen prescrito), o a cantidades que aunque no intervengan en el proceso de optimización, queremos que se mantengan conocidas o controladas a lo largo del mismo (p.e. centro de masa); veremos cómo especificar esto en la tabla "tipo de cantidad" de abajo.

La sintaxis general para implementar una cantidad en Evolver es:

quantity "nombre" [tipo de cantidad] method [método] [opción global]

Vamos a explicar cada elemento de la línea anterior.

Vamos a pasar ahora a listar una serie de métodos usuales. Pueden implementarse nuevos métodos, pero esto requiere escribir rutinas en lenguaje C.

Métodos 0-dimensionales

Nombre y descripción del método Ejemplo
vertex_scalar_integral
Integral de una función valuada escalar sobre un punto (i.e. evaluar la función en un vértice). La función se define mediante scalar_integrand.		 quantity point_value energy method vertex_scalar_integral
scalar_integrand: x^2 + y^2 - 2x + 3

Métodos 1-dimensionales

Nombre y descripción del método Ejemplo
edge_tension o edge_length
Longitud de una curva.		 quantity len energy method edge_length global
density_edge_length
Longitud de un lado, multiplicado por su densidad.		 quantity len energy method density_edge_length glob
edge_scalar_integral
Integral de una función valuada escalar sobre una curva p.p.a. (p.e. la longitud de una curva). La función se define mediante scalar_integrand. En el ejemplo, se estudia la integral de la función x^2-3y+4 sobre un lado, vista como energía.		 quantity edge_sint energy method edge_scalar_integral
scalar_integrand: x^2 - 3*y + 4
edge_vector_integral
Integral del producto escalar de un campo sobre una curva con el normal unitario a lo largo de ésta (p.e. el área en el string model o al prescribir un ángulo en problemas de capilaridad). El campo se define por sus coordenadas (q1,q2,q3).		 quantity edge_vint energy method edge_vector_integral
vector_integrand:
q1: 0
q2: 0
q3: z^2/2
edge_general_integral
Integral sobre una curva de una función escalar que depende de la posición (x1,x2,x3) y de un vector tangente (x4,x5,x6) en ese punto. El integrando debe ser homogéneo de grado 1 en las variables x4,x5,x6.		 quantity arclength energy method edge_general_integral
scalar_integrand: sqrt(x4^2 + x5^2 + x6^2)
edge_area
Area de un recinto 2D en el string mode. Sobre un lado orientado L, es igual a la integral de -y dx a lo largo de L (o sea, mide el opuesto del área del recinto encerrado por L y el eje x junto con los lados paralelos al eje y que pasan por los extremos de L). Si esto se repite para cada lado del borde de un recinto, se consigue el área encerrada por éste.		 quantity cell1_area fixed = 1.3 method edge_area
edge_torus_area
Lo mismo del anterior, pero cuando se trabaja en un toro 2D.Hay que asignar un valor numérico a la cantidad volconst, ya que el cálculo del área de un recinto sólo está definido módulo el área total del toro.		 quantity cell_area fixed = 1.3 method edge_torus_area
string_gravity
Calcula la energía potencial (gravitacional) de un recinto bidimensional $\Omega$ en el string model, dada por \[\int_\Omega G\rho y\ dA=\frac{G\rho}{2}\int_{\partial\Omega}\langle(0,y^2),N\rangle ds,\] donde $G$ es la constante gravitatoria, $\rho$ es la densidad del recinto y $N$ el campo normal unitario exterior a $\partial\Omega$.		 quantity cell_grav energy modulus 980*8.5 method string_gravity
sqcurve_string
Integral de la curvatura al cuadrado a lo largo de una curva (sus puntos críticos son las curvas elásticas). Asume que en cada vértice sólo concurren dos lados, y da el valor cero a los extremos de una curva si es abierta. Para especificar otras potencias de la curvatura, usar el parámetro parameter_1.		 quantity sq energy method sqcurve_string global
parameter_1 3
metric_edge_length
Longitud de una curva en el string model, respecto a una métrica Riemanniana dada, que se dará usando el comando metric.		 string
space_dimension 2
metric
1+x^2 y
y 1+y^2
quantity mel energy method metric_edge_length global

Métodos 2-dimensionales

Nombre y descripción del método Ejemplo
facet_tension o facet_area
Area de una superficie o de una cara. No multiplica por la densidad de la cara (para ello usar density_facet_area).		 quantity farea energy method facet_area global
density_facet_area
Area de una cara multiplicada por su densidad.		 quantity farea energy method density_facet_area global
facet_volume
Volumen de un recinto 3D en el soapfilm mode. Sobre una cara orientada $C$, es igual a la integral de $z\ dx\ dy$ a lo largo de $C$ (osea, mide el volumen del recinto encerrado por $C$, el plano $\{z=0\}$ junto con los planos verticales que pasan por los segmentos en el borde de $C$). Si esto se repite para cada cara del borde de un recinto, se consigue el volumen encerrado por éste. 		quantity vol fixed = 1.3 method facet_volume
facet_torus_volume
Lo mismo del anterior, pero cuando se trabaja en un toro 3D. Hay que asignar un valor numérico a la cantidad volconst, ya que el cálculo del área de un recinto sólo está definido módulo el volumen total del toro.		 quantity body_vol energy method facet_torus_volume
facet_scalar_integral
Integral de una función valuada escalar sobre una superficie (p.e. el área de una superficie en el soapfilm model). La función se define mediante scalar_integrand.		 quantity fint energy method facet_scalar_integral global
scalar_integrand: x^2+y^2
facet_vector_integral
Integral a lo largo de una cara, del producto escalar de un campo con el normal unitario a una superficie. El normal se elige por la regla de la mano derecha. El campo se define usando vector_integrand. El ejemplo define el volumen multiplicado por 3 del recinto "entre" una cara y el plano $\{z=0\}$:		 quantity fvint energy method facet_vector_integrand
vector_integrand:
q1: 0
q2: 0
q3: z
facet_general_integral
Integral sobre una cara de una función escalar que depende de la posición (x1,x2,x3) y del vector normal a la cara (x4,x5,x6). El integrando debe ser homogéneo de grado 1 en las variables x4,x5,x6. La función se define mediante scalar_integrand.		 quantity surfacearea energy method facet_general_integral
scalar_integrand: sqrt(x4^2 + x5^2 + x6^2)
gravity_method o full_gravity_method
Calcula la energía potencial (gravitacional) de un recinto 3D $\Omega$ en el soapfilm model, dada por\[\int_\Omega G\rho z\ dV=\frac{G\rho}{2}\int_{\partial\Omega}\langle(0,0,z^2),N\rangle dA,\] donde $G$ es la constante gravitatoria, $\rho$ es la densidad del recinto y $N$ el campo normal unitario exterior a $\partial\Omega$.		 quantity grav energy modulus 980*8.5 method gravity_method
metric_facet_area
Area de una cara en el soapfilm model, respecto a una métrica Riemanniana dada, que se dará usando el comando metric.		 metric
1+x^2 0 z
0 1+y^2 0
z 0 1+z^2
quantity mfa energy method metric_facet_area globa
mean_curvature_integral
Integral de la curvatura media de una superficie.		 quantity mci energy method mean_curvature_integral
sq_mean_curvature
Integral del cuadrado de la curvatura media sobre una superficie (funcional de Willmore). Sus puntos críticos son las superficies de Willmore. Hay variantes de este método, que incluso permiten aplicarlo a superficies con borde o configuraciones más generales (como eff_area_sq_mean_curvature, normal_sq_mean_curvature, star_sq_mean_curvature, star_eff_area_sq_mean_curvature, star_normal_sq_mean_curvature, star_perp_sq_mean_curvature)		 quantity sqc energy method sq_mean_curvature global
gauss_curvature_integral
Integral de la curvatura de Gauss de una superficie con borde (el caso sin borde está dado por la fórmula de Gauss-Bonnet).		 quantity gint energy method gauss_curvature_integral global
spherical_area
Area de la proyección de una cara sobre la esfera unidad. Se supone que los vértices de la cara pertenecen a la esfera unidad. Suele estar acompañado por la ligadura de que los vértices se muevan en la esfera unidad.		 constraint 1 formula: x^2 + y^2 + z^2 = 1
quantity spharea energy method spherical_area global

A continuación veremos tres ejemplos para explicar el uso de cantidades definidas por el usuario.

La catenaria

Imaginemos un cable inextensible que cuelga entre dos soportes, bajo la acción de la gravedad. En esta situación, la naturaleza minimiza la energía gravitacional del cable. El mínimo para este problema es un trozo de catenaria, es decir, la gráfica de la función

\[y=a\cdot\mbox{cosh}(bx)\]

($a$, $b$ son parámetros reales, e $y$ mide la altura). Se trata de un problema 1D (string model) en un espacio 2D (el plano $(x,y)$ que contiene a los soportes y al cable), donde minimizaremos la energía gravitacional. Como el cable es inextensible, debemos fijar la longitud de la curva como cantidad tipo fixed. Podríamos hacer esto usando el método genérico edge_scalar_integral con la función sqrt(x^2+y^2), pero usaremos el método edge_length, que hace lo mismo y es más rápido (por tener implementado un código específico). El fichero de datos es catenary.fe, cuya configuración inicial es la siguiente:

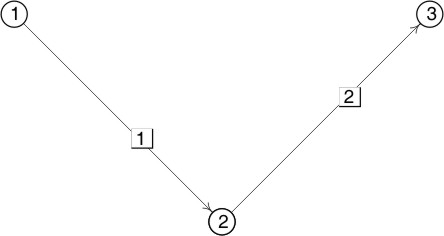
Esquema de la catenaria 
// catenary.fe
// String of fixed length hanging between supports,
// minimizing gravitational energy.

space_dimension 2
string

quantity grav energy method edge_scalar_integral global  Aquí se define la energía a minimizar.
scalar_integrand: y

quantity arclength fixed = 3 method edge_length global

vertices
1   -1 1 fixed    Los soportes del cable están fijos
2    0 0
3    1 1 fixed

edges
1    1 2 tension 0   Los soportes no producen tensión sobre el cable, sólo la gravedad.
2    2 3 tension 0

Si ejecutamos catenary.fe y lo evolucionamos con

r; g 5; r; g5; r; g 5

tendremos una buena aproximación de una catenaria. Para ver los valores de las cantidades usadas, teclearemos v, obteniendo

Enter command: v
Quantity target value actual value pressure
grav --------- 1.18616662825846  
arclength 3 3.00000000006522 -0.619645...

La interpretación del campo pressure anterior es el cambio del valor de la energía.

Curvas elásticas

Las curvas elásticas en $\mathbb{R}^3$ son puntos críticos del funcional bending energy en dimensión 1, que es

\[F_\lambda(\gamma)=\int_\gamma(\kappa^2+\lambda)ds\]

donde $\gamma$ es una curva cerrada en $\mathbb{R}^3$, $\kappa$ es su curvatura y $\lambda$ un parámetro real. Los puntos críticos del funcional anterior son las soluciones de la EDO de segundo orden

\[2\kappa''+\kappa^3-\lambda\kappa=0\]

Implementaremos con Evolver una curva elástica plana, para el funcional con $\lambda=0$ y con la topología de un ocho. El fichero de datos es elastic8.fe, y la configuración inicial

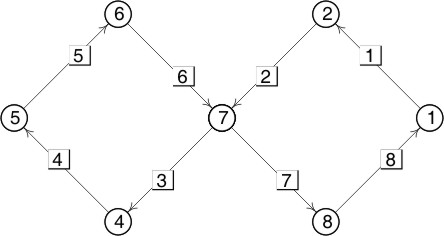
Esquema de la curva elástica 
// elastic8.fe
// Elastic string in the shape of a figure 8.

string
space_dimension 2
scale_limit 0.1  // else blows up on first iteration El comando scale_limit da una cota superior de la magnitud de la evolución permitida desde una configuración a la siguiente. En este caso, si no pusiéramos esta limitación la evolución se dispararía.

quantity bending_energy  energy method sqcurve_string global Definimos la energía a minimizar, con el método sqcurve_string

quantity arclength fixed = 14 method edge_length global Prescribimos la longitud de la curva con el valor 14 y e método edge_length

vertices
1    2 0
2    1 1
3    0 0
4   -1 -1
5   -2 0
6   -1 1
7    0 0
8    1 -1

edges
1  1 2 tension 0
2  2 3 tension 0
3  3 4 tension 0
4  4 5 tension 0
5  5 6 tension 0
6  6 7 tension 0
7  7 8 tension 0
8  8 1 tension 0

Superficies de Willmore

El funcional de Willmore es el funcional bending energy en dimensión 2, definido por

\[F(M)=\int_M H^2\ dA\]

donde $M$ es una superficie compacta en $\mathbb{R}^3$ y $H$ es su curvatura media. Las superficies de Willmore son los puntos críticos de este funcional. El mínimo absoluto del funcional de Willmore es $4\pi$ y se alcanza únicamente en la esfera redonda (no importa el radio, puesto que el funcional de Willmore es invariante al reescalar):

Sea $M\subset\mathbb{R}^3$ una superficie compacta y embebida, con normal exterior $N$, curvaturas principales $k_1,k_2$ respecto a $N$ y curvatura de Gauss $K=k_1k_2$. Como $H^2-K=\frac{1}{4}(k_1-k_2)^2\geq 0$, deducimos que
$H^2\geq \max (0,K):=K^+$. Así,
\[
\int _MH^2\, dA\geq \int _MK^+\, dA\stackrel{\text{(Chen-Lashoff)}}{\geq }4\pi .
\]
Y si $F(M)=4\pi $, entonces de lo anterior se deduce que $H^2=K^+$ en $M$, y por tanto todos los puntos del conjunto $\{ p\in M \ | \ K(p)\geq 0\} $ son umbilicales. Tomemos un punto $q\in M$ tal que $K(q)>0$. Por continuidad, existe un entorno $V$ de $q$ en $M$ tal que $K|_V>0$, y por lo anterior $V$ está compuesto exclusivamente por puntos umbilicales con curvatura positiva. Esto implica (podemos elegir $V$ conexo) que $V$ está contenido en una esfera de cierto radio $R=R(q)>0$, luego $K=1/R^2$ en $V$. Consideremos el conjunto $A=\{ p\in M \ | \ K(p)=1/R^2\} $. Por lo anterior, $A$ es un abierto no vacío de $M$. Como $A$ es triviamente cerrado en $M$, deducimos que $A$ es una componente conexa de $M$. Pero $M$ ha de ser conexa (cada componente conexa de $M$ produce al menos $4\pi $ en el funcional de Willmore), luego $A=M$ y $M$ es una esfera.

Los puntos críticos del funcional de Willmore se llaman superficies de Willmore. Puede comprobarse que la ecuación de Euler-Lagrange asociada a este funcional es la EDP no lineal
\[
\Delta H+2H(H^2-K)=0.
\]
El funcional de Willmore es invariante por cambios conformes, y con métodos variacionales puede probarse que para cada género g existe una superficie de Willmore compacta y embebida en $\mathbb{R}^3$ con género $g$. La famosa conjetura de Willmore establece que para toros  en $\mathbb{R}^3$, el funcional de Willmore  es siempre mayor o igual que $2\pi^2$ (la igualdad se alcanza en un toro de revolución cuyas circurferencias generatrices tienen los radios en la relación $1:\sqrt{2}$). Una forma de obtener superficies de Willmore en $\mathbb{R}^3$ es proyectar estereográficamente superficies mínimas de $\mathbb{S}^3$.

El funcional de Willmore puede ser usado para representar con Evolver superficies mínimas no necesariamente estables, ya que la condición H = 0 minimiza trivialmente el funcional de Willmore, considerado ahora sobre superficies con borde. En el fichero pcellbox.fe se usa el funcional de Willmore para producir la superficie P-Schwarz, pero donde ahora no estamos considerando la superficie dentro de un toro llano tridimensional sino dentro de una caja $[0,1]^3$. Cada una de las 6 caras de la caja es una ligadura, donde se moverá una curva borde de la superficie.

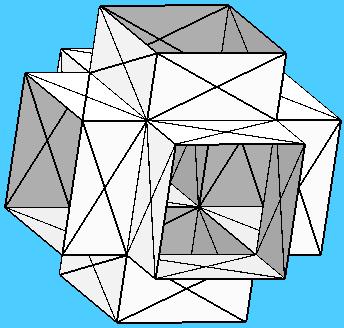
Configuración inicial para P-Schwarz 
// pcellbox.fe
// Evolver data for cubic unit cell of the P surface.

// For demonstrating squared mean curvature
quantity sqmean energy modulus 0 method star_perp_sq_mean_curvature global Definimos la energía a minimizar, mediante el método sq_mean_curvature implementado originalmente para el funcional de Willmore)

constraint 1 /* the left side */  Definimos las 6 ligaduras correspondientes a las caras de la caja.
function: y = 0

constraint 2 /* the right side */
function: y = 1

constraint 3 /* the front side */
function: x = 1

constraint 4 /* the back side */
function: x = 0

constraint 5 /*the bottom*/
function: z = 0

constraint 6 /*the top*/
function: z = 1

vertices
9 .25 .25 0.0 constraint 5  Vértices en la base de la caja
10 .75 .25 0.0 constraint 5
11 .75 .75 0.0 constraint 5
12 .25 .75 0.0 constraint 5
13 .25 .25 1.0 constraint 6 Vértices en la cara superior de la caja
14 .75 .25 1.0 constraint 6
15 .75 .75 1.0 constraint 6
16 .25 .75 1.0 constraint 6
33 .25 .25 0.25 Vértices interiores a la caja (8)
34 .75 .25 0.25
35 .75 .75 0.25
36 .25 .75 0.25
37 .25 .25 0.75
38 .75 .25 0.75
39 .75 .75 0.75
40 .25 .75 0.75
17 .25 0.0 0.75 constraint 1        Vértices en la cara de la izquierda de la caja
18 .75 0.0 0.75 constraint 1
19 .75 0.0 0.25 constraint 1
20 .25 0.0 0.25 constraint 1
21 .25 1.0 0.75 constraint 2        Vértices en la cara de la derecha de la caja
22 .75 1.0 0.75 constraint 2
23 .75 1.0 0.25 constraint 2
24 .25 1.0 0.25 constraint 2
25 1.0 .25 0.75 constraint 3        Vértices en la cara frontal de la caja
26 1.0 .25 0.25 constraint 3
27 1.0 .75 0.25 constraint 3
28 1.0 .75 0.75 constraint 3
29 0.0 .25 0.75 constraint 4        Vértices en la cara posterior de la caja
30 0.0 .25 0.25 constraint 4
31 0.0 .75 0.25 constraint 4
32 0.0 .75 0.75 constraint 4

edges /* given by endpoints and attribute */
13 9 10 constraint 5  Lados en la base de la caja
14 10 11 constraint 5
15 11 12 constraint 5
16 12 9 constraint 5
17 13 14 constraint 6 Lados en la cara superior
18 14 15 constraint 6
19 15 16 constraint 6
20 16 13 constraint 6
21 17 18 constraint 1 Lados en la cara izquierda
22 18 19 constraint 1
23 19 20 constraint 1
24 20 17 constraint 1
25 21 22 constraint 2 Lados en la cara derecha
26 22 23 constraint 2
27 23 24 constraint 2
28 24 21 constraint 2
29 25 26 constraint 3 Lados en la cara frontal
30 26 27 constraint 3
31 27 28 constraint 3
32 28 25 constraint 3
33 29 30 constraint 4 Lados en la cara posterior
34 30 31 constraint 4
35 31 32 constraint 4
36 32 29 constraint 4
37 33 34  Lados interirores
38 34 35
39 35 36
40 36 33
41 37 38
42 38 39
43 39 40
44 40 37
45 33 37
46 34 38
47 35 39
48 36 40
49 9 33
50 10 34
51 11 35
52 12 36
53 13 37
54 14 38
55 15 39
56 16 40
57 17 37
58 18 38
59 19 34
60 20 33
61 21 40
62 22 39
63 23 35
64 24 36
65 25 38
66 26 34
67 27 35
68 28 39
69 29 37
70 30 33
71 31 36
72 32 40

faces /* given by oriented edge loop */
1 49 37 -50 -13
2 50 38 -51 -14
3 51 39 -52 -15
4 -16 52 40 -49
5 17 54 -41 -53
6 18 55 -42 -54
7 19 56 -43 -55
8 20 53 -44 -56
9 57 41 -58 -21
10 58 -46 -59 -22
11 59 -37 -60 -23
12 60 45 -57 -24
13 25 62 43 -61
14 26 63 47 -62
15 27 64 -39 -63
16 28 61 -48 -64
17 29 66 46 -65
18 30 67 -38 -66
19 31 68 -47 -67
20 32 65 42 -68
21 72 44 -69 -36
22 69 -45 -70 -33
23 70 -40 -71 -34
24 71 48 -72 -35

bodies /*defined by its oriented faces */
1 -1 -2 -3 -4 -5 -6 -7 -8 -9 -10 -11 -12 -13 -14 \
-15 -16 -17 -18 -19 -20 -21 -22 -23 -24

read

Una buena secuencia para evolucionar lo anterior es:

r; u; g10; r; u; g10
Joaquín Pérez © 2011
Inicio  |   Arriba