Tutorial 7
Simetrías
Hemos visto que ciertos procesos de optimización producen superficies que tienen una simetría en un plano, como ocurre con los problemas de frontera libre o cuando estamos resolviendo un problema de Plateau y el borde prescrito es simétrico por reflexión en un plano. Por ejemplo, consideremos un problema de Plateau cuyo borde consiste en dos cuadrados horizontales como en la siguiente figura:
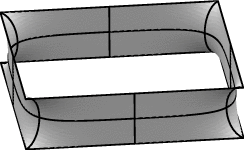
La figura anterior tiene 5 planos de simetría: cada uno de los tres planos coordenados {x = 0}, {y = 0}, {z = 0} (estamos situando el origen en el centro de la figura), y dos planos verticales en diagonal. Estos planos dividen la superficie en 16 regiones congruentes, llamadas dominios fundamentales. Esto quiere decir que si hacemos que Evolver calcule sólo uno de los dominios fundamentales, entonces podremos generar la figura completa mediante reflexión en los planos anteriores. Y hacer la optimización sobre 1/16 de la figura completa significa dividir por 16 el número de cálculos y multiplicar por 16 la velocidad de optimización.
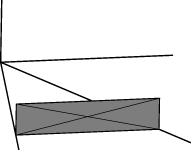
El fichero sqcat.fe produce por refinamiento-iteración un dominio fundamental para el problema anterior:
 |
 |
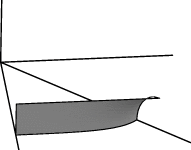| La configuración inicial en sqcat.fe. | La superficie una vez optimizada. |
Evolver puede generar diferentes vistas de una misma figura, usando aplicaciones afines. Una aplicación afín es una aplicación $f:\mathbb{R}^3\rightarrow\mathbb{R^3}$ del tipo
\[ f\left(\begin{array}{c} x_1\\x_2\\x_3\end{array}\right)=\left(\begin{array}{ccc}a & b & c\\d & e & f\\g & h & i \end{array}\right) \left(\begin{array}{c} x_1\\x_2\\x_3\end{array}\right) +\left(\begin{array}{c} v_1\\v_2\\v_3\end{array} \right) \]donde estamos usando coordenadas respecto a la base usual de $\mathbb{R}^3$. Para representar la aplicación anterior, Evolver usa la sintaxis (coordenadas homogéneas)
a b c v1
d e f v2
g h i v3
0 0 0 1
Volviendo al caso anterior, uno puede definir 15 matrices de aplicaciones afines, que generen cada uno de los 15 dominios fundamentales distintos de uno dado (la identidad produce la imagen original, que ya tenemos) pero esto es bastante tedioso. En lugar de ello, uno puede aplicar sólo unas cuantas simetrías, que generen la figura completa a partir de un dominio fundamental. Llamamos a estas simetrías generadores, y el comando que genera composiciones de estos generadores es
view_transform_generators n
donde n es el número de generadores que usaremos. En el caso anterior, con tres generadores tendremos suficiente (la simetrías respecto de los planos {z = 0}, {y = 0}, {x = y}). Lo siguiente es un trozo del fichero sqcat.fe donde se definen estos generadores:
// For viewing multiple copies of the fundamental region
view_transform_generators 3
// generator A: reflection in z_mirror
1 0 0 0
0 1 0 0
0 0 -1 0
0 0 0 1
// generator B: reflection in y_mirror
1 0 0 0
0 -1 0 0
0 0 1 0
0 0 0 1
// generator C: reflection in xy_mirror
0 1 0 0
1 0 0 0
0 0 1 0
0 0 0 1
y ahora, tecleando los comandos de la columna de la izquierda conseguiremos los resultados en la columna de la derecha:
| transform_expr "a" |  |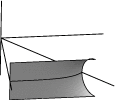
| transform_expr "b" |  |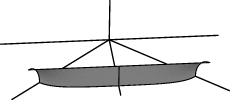
| transform_expr "c" |  |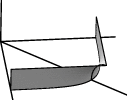
| transform_expr "ab" |  |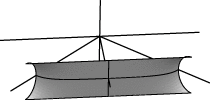
| transform_expr "abc" |  |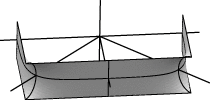
| transform_expr "abcabc" |  |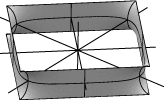
Evolver genera, a partir de una cadena de n letras (generadores), todas aquellas transformaciones de la figura original que se corresponden a aplicar cualquier sub-cadena ordenada dentro de la cadena original, descartando aquellas sub-cadenas que sólo produzcan repeticiones respecto de las ya calculadas. Para eliminar imágenes múltiples (generadas por el proceso anterior) y volver a la figura original, teclearemos
transforms off
Si queremos volver a activar la última imagen multiple generada, teclearemos
transforms on
A continuación comentamos el fichero completo sqcat.fe.
// sqcat.fe
// Catenoid between parallel squares.
// One fundamental region,
bounded by mirror planes.
parameter height = 0.25 // half-distance between squares Definimos el
parámetro "height" = semidistancia entre los bordes de la superficie completa
// Mirror plane constraints Ligadura "z-mirror": el plano de simetría z = 0.
constraint z_mirror
formula: z = 0
constraint y_mirror Ligadura "y-mirror": el plano de simetría y = 0.
formula: y = 0
constraint xy_mirror Ligadura "xy-mirror": el plano de simetría x = y (nótese que no hemos usado la fórmula f = 0)
formula: x = y
// For viewing multiple copies of the fundamental region
view_transform_generators 3
// generator A: reflection in z_mirror Esta es la parte que comentamos arriba
1 0 0 0
0 1 0 0
0 0 -1 0
0 0 0 1
// generator B: reflection in y_mirror
1 0 0 0
0 -1 0 0
0 0 1 0
0 0 0 1
// generator C: reflection in xy_mirror
0 1 0 0
1 0 0 0
0 0 1 0
0 0 0 1
vertices Ahora la superficie inicial.
1 1 0 height fixed // half-side of square frame Nótese que la tercera coordenada es el parámetro height
2 1 1 height fixed Los vértices 1,2 son fijos porque están en el borde.
3 1 0 0 constraints z_mirror,y_mirror // contact line on z_mirror Los vértices 3,4 son móviles pero sometidos a ligaduras (intersección de 2 planos)
4 1 1 0 constraints z_mirror,xy_mirror
// Some coordinate axes, just to help viewer get oriented Los vértices 5,6,7,8,9 sirven para formar ejes coordenados y rectas auxiliares (todo fijo)
5 0 0 0 fixed
6 1.2 0 0 fixed
7 0 1.2 0 fixed
8 0 0 0.5 fixed
9 1.2 1.2 0 fixed
edges
1 1 2 fixed // half-side of square frame Lado fijo, ya que forma parte del borde.
2 1 3 constraint y_mirror // contact line on y_mirror Los lados 2,3,4 son móviles pero sometidos a ligaduras.
3 3 4 constraint z_mirror // contact line on z_mirror
4 4 2 constraint xy_mirror // contact line on xy_mirror
// axes
5 5 6 fixed bare no_refine Los lados 5,6,7,8 son ejes auxiliares, fijos y no refinables.
6 5 7 fixed bare no_refine
7 5 8 fixed bare no_refine
8 5 9 fixed bare no_refine
faces
1 2 3 4 -1
read
// simple evolution Lo que sigue es un ejemplo de cómo evolucionar la configuración inicial.
gogo := {
refine edge where length > .6;
r;
g 10;
r;
g 10;
hessian;
hessian;
}
Periodicidad. Problemas en un cociente del plano o del espacio
En ocasiones, debemos estudiar problemas de optimización donde no existen bordes, pero las interfases a considerar tienen longitud o área finita en cierto sentido. Por ejemplo, imaginemos que estamos estudiando las propiedades de cierto tipo de espuma, formada por gran cantidad de pompas de jabón que se unen formando complicadas estructuras como la de la figura siguiente:
Esta estructura minimiza la cantidad de material (película de jabón) necesario para encerrar un determinado volumen. La estructura de las pompas de jabón al unirse no es arbitraria, sólo ciertos ángulos están permitidos cuando tres o más pompas se encuentran en una arista común. Dicha estructura, aunque compleja, tiende a repetirse si consideramos porciones suficientemente grandes de espuma, o equivalentemente, si el tamaño medio de las pompas de jabón que la componen es suficientemente pequeño en relación con el recipiente que la contiene. Sin embargo, no estamos interesados en la disposición que adoptan las pompas de jabón que están en contacto con las paredes del recipiente que contiene a la espuma, ya que la forma de esas pompas "frontera" depende esencialmente de cómo son las paredes del recipiente. En cierto sentido, el universo ideal donde estudiar la espuma sería un universo de volumen finito sin paredes. Pues bien, matemáticamente existe un universo como éste: un toro llano tridimensional $\mathbb{T}^3$, que es el espacio resultante de identificar en un cubo ordinario (en realidad, puede hacerse lo mismo con cualquier paralelepípedo) las caras opuestas por medio de una traslación. Pensemos en el cubo unidad $[0,1]\times[0,1]\times[0,1]\subset\mathbb{R}^3$, con sus caras identificadas por las traslaciones de vectores $(1,0,0)$, $(0,1,0)$, $(0,0,1)$.
Un objeto en el interior del cubo, que semueva en la dirección de $(0,1,0)$ saldrá del cubo por su cara lateral derecha, para volver a entrar inmediatamente por el lugar homólogo en la cara lateral izquierda, y tras seguir su movimiento rectilíneo, volverá a pasar exactamente por el mismo punto en el que comenzó su movimiento, tal y como ocurre con la nave espacial es la secuencia de imágenes siguiente.
Sin embargo, la "pared" del cubo no existe como tal en $\mathbb{T}^3$, luego aparentemente el objeto ha seguido una trayectoria rectilínea y finita sin atravesar ningún obstáculo, tal y como haría en el espacio ordinario $\mathbb{R}^3$, con la salvedad de que termina por volver al punto de partida. En ese sentido, si un observador $O$ situado en el centro del cubo mira a su derecha, entonces verá una copia $O'$ de sí mismo a distancia horizontal 1, de la misma forma que un observador en $\mathbb{R}^3$ vería su imagen por la traslación de vector $(1,0,0)$. Pero la visual de $O$ hacia $O'$ no se detiene allí, y seguiría viendo infinitas copias $O',O'',O''',...$ de $O$, todas ellas consecutivas y a distancia horizontal 1 unas de otras a la derecha de $O$, cada vez más pequeñas por efecto de la distancia creciente a $O$. Y lo mismo podemos decir si el observador mira a su izquierda. Este efecto de periodicidad se repite también usando las caras "arriba - abajo" y "delante - detrás". Puedes ver el efecto en el video siguiente, del que las tres figuras anteriores son fotogramas aislados. En él vemos un universo modelado en $\mathbb{T}^3$, que contiene fos estrellas y una nave espacial en movimiento (pulsar este enlace para ver un vídeo de esta situación).
El espacio $\mathbb{T}^3$ tiene volumen 1 y no tiene bordes. Una forma de visualizar $\mathbb{T}^3$ es pensando en $\mathbb{R}^3$ dividido en infinitas copias adyacentes del cubo unidad, es decir, con una malla 3D de celdas cúbicas con arista de longitud 1. A cada una de estas celdas se la llama dominio fundamental. En cada celda veremos una copia idéntica de lo que ocurre en $[0,1]^3$. Por ejemplo, en el caso de nuestro universo de dos estrellas y una nave, en el modelo de malla 3D en $\mathbb{R}^3$ nos parecerá que tiene infinitas naves y estrellas (pulsar este enlace para ver otro video).
Para explicar cómo optimizar problemas periódicos con Evolver, usaremos tres ejemplos, el primero 2D y los otros dos 3D.
El primero de los ejemplos optimiza la longitud de cierta configuración en $\mathbb{T}^2$, y un símil físico del problema a considerar podría ser el siguiente: imaginemos que vivimos sobre un planeta cuya superficie es un toro $\mathbb{T}^2$, que no tenemos medios para separarnos de la superficie del mismo y que nos encargan el trabajo de construir dos ciudades y una red de tres carreteras entre ellas, de forma que dos carreteras se "enrollen" en las direcciones de los dos generadores del grupo fundamental de $\mathbb{T}^2$. Nos piden situar tanto las ciudades como las carreteras de forma que gastemos el mínimo material posible en asfaltarlas, lo que se traduce en minimizar la longitud total de las mismas. Para Evolver, la configuración consiste en dos vértices unidos por 3 aristas.
En la siguiente figura, el cuadrado en azul sólo se representa para facilitar la localización de la figura; no forma parte de la configuración.
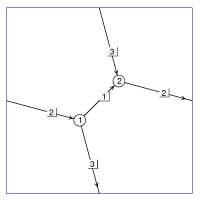
Si vemos la configuración anterior en el plano, aparece una figura doblemente periódica. De nuevo los cuadrados son auxiliares.
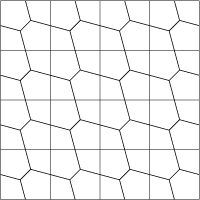
Si eliminamos los cuadrados, que realmente no forman parte del problema, obtendremos lo que realmente percibe un observador que viva en este toro llano bidimensional.
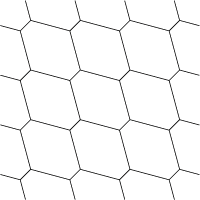
Para trabajar con Evolver en un toro 2D, simplemente teclearemos
torus
periods
1 0
0 1
donde $(1,0)$ y $(0,1)$ son los vectores que generan el retículo de $\mathbb{R}^2$ que produce el toro. A continuación enumeramos los vértices, como siempre. No importa si las coordenadas de los vértices están todas en el mismo dominio fundamental (en este caso, el cuadrado unidad). Introducir los lados es algo más complicado, ya que un lado podría salir del dominio fundamental para volver a entrar por el lado opuesto, y esto para cada dimensión. Por ello, además del dígito habitual que identifica el lado y los dígitos de sus vértices extremos (en orden), teclearemos una lista de n (=dimensión) símbolos de entre los 3 siguientes:
- + para indicar que el lado sale por el lado positivo del dominio fundamental, para volver a entrar en el mismo por el lado negativo opuesto (positivo y negativo se toman respecto del correspondiente período generador del retículo).
- - para indicar que el lado sale por el lado negativo del dominio fundamental, para volver a entrar en el mismo por el lado positivo.
- * para indicar que el lado no sale ni entra del dominio fundamental en esa "dirección".
Por ejemplo, los lados 1,2,3 del ejemplo que estamos explicando se escriben
1 1 2 * *
2 2 1 + *
3 1 2 * -
Las caras y cuerpos se introducen como siempre. Veamos ya el fichero tor2D.fe completo:
// tor2D.fe
// Simple example of 2D torus
space_dimension 2 Indica que estamos en un espacio bidimensional, con el string model (minimización de longitud)
string
torus
periods
1 0
0 1
vertices
1 .3 .3
2 .7 .7
edges
1 1 2 * *
2 2 1 + *
3 1 2 * -
faces
1 1 -3 -2 -1 3 2
bodies
1 1 Definimos un solo dominio; esto será importante a la hora de representar gráficamente, como veremos más abajo.
read
Cuando ejecutamos tor2D.fe y tecleamos s (show graphics), nos preguntará por una de tres opciones de representación gráfica:
- Opción 0: raw facets (raw = "en bruto"). Dibuja los lados vistos
en $\mathbb{R}^2$, sin tener en cuenta cómo se "enrollan" en el toro,
situados a partir de sus extremos iniciales sobre el dominio
fundamental.
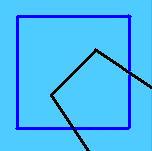
- Opción 1: connected bodies. Dibuja los lados en $\mathbb{R}^2$
de forma que los cuerpos siempre sean conexos y cerrados.
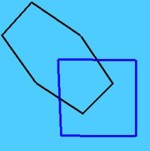
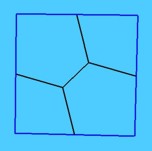
- Opción 2: clipped. Dibuja la intersección de la configuración
con el dominio fundamental determinado por los vectores período que
hemos especificado.
En cualquiera de las tres opciones, al teclear o haremos visible o invisible el borde del dominio fundamental.
Si queremos obtener copias adyacentes de dominios fundamentales para ver trozos mayores de nuestra configuración periódica, teclearemos el comando (debemos estar en modo de comandos) y n donde n indica la dirección en la que queremos duplicar, en nuestro caso n = 1 ó n = 2. Este comando es acumulativo, de forma que la secuencia
y 1
y 2
primero duplicará el dominio fundamental horizontalmente, y luego duplicará este resultado verticalmente, obteniendo cuatro copias del dominio fundamental original. Si ahora tecleamo
v
entonces Evolver asignará nuevos cuerpos individuales a cada uno de los duplicados obtenidos (ahora tenemos 4). Con esta configuración de 4 cuerpos, se verá más claro el uso de "connected bodies": tecleamos
connected
y veremos los 4 cuerpos de forma conexa.
Ejemplo de optimización en un toro $\mathbb{T}^3$: la superficie P de Schwarz
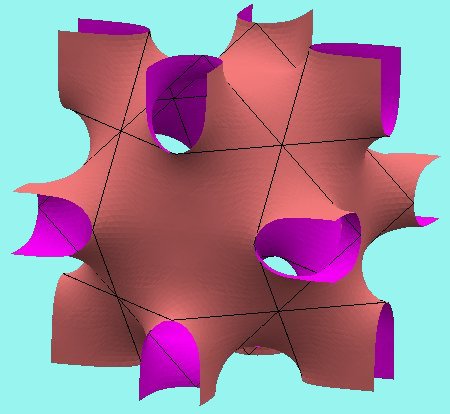
En el siglo XIX, Schwarz consideró el problema de encontrar superficies mínimas cuyo borde es una línea poligonal cerrada que no esté contenida en un plano. El caso más sencillo de un polígono de este tipo es un cuadrilátero con lados de la misma longitud, como el que aparece resaltado en la siguiente figura.
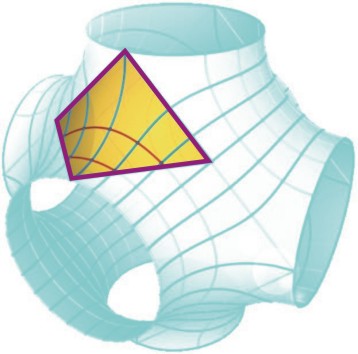
El problema de Plateau asociado a dicho contorno tiene solución única D que es topológicamente un disco, y el principio de reflexión de Schwarz nos permite reflejar D respecto a cada segmento en su frontera. Si el ángulo que forman los dos triángulos cuya unión es el cuadrilátero frontera de D es el adecuado, entonces tras reflejar indefinidamente obtendremos una superficie S sin autointersecciones (embebida). Como la composición de dos reflexiones respecto de rectas paralelas es una traslación, no es difícil ver que S es invariante por tres traslaciones de vectores linealmente independientes (es decir, S es triplemente periódica). Esta periodicidad de S permite inducirla a una superficie $\bar{S}$ en un toro cúbico $\mathbb{T}^3$. La figura muestra la parte de S dentro de un dominio fundamental de $\mathbb{T}^3$.
Debido a sus simetrías, la superficie $\bar{S}$ divide a $\mathbb{T}^3$ en dos regiones de igual volumen. Esta característica nos va a permitir implementar $\bar{S}$ mediante Evolver, minimimizando el área e imponiendo de el volumen una de las dos regiones en $\bar{S}$ que divide a tenga volumen la mitad del volumen de $\mathbb{T}^3$.
Tomaremos la siguiente configuración inicial:
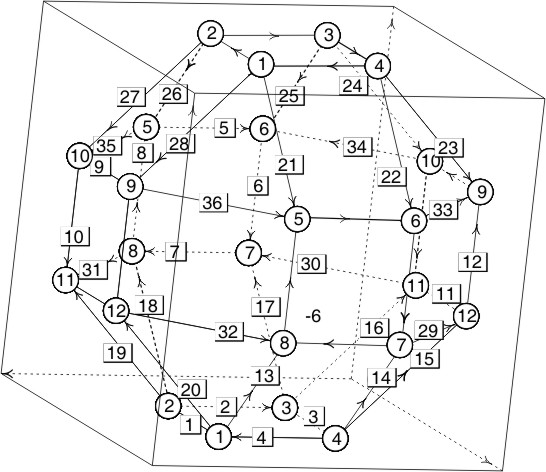
A continuación transcribimos el fichero schwarz1.fe insertando comentarios.
// P-Schwarz
TORUS_FILLED Cuando uno trabaja en un ambiente compacto, puede que rellenemos el volumen total con distintos cuerpos; en este caso, es redundante imponer un volumen prescrito para cada uno de los cuerpos, ya que uno de los volúmenes será el total menos la suma de los restantes. El problema técnico que se presenta cuando uno tiene volúmenes prescritos redundantes es que el método que Evolver usa para imponer esas restricciones sobre volumen necesita invertir cierta matriz, y esa matriz es singular en este caso. Con el comando TORUS_FILLED aseguramos que uno de los volúmenes permanece siempre sin prescribir y evitamos así el problema.
periods
3.000000 0.000000 0.000000
0.000000 3.000000 0.000000
0.000000 0.000000 3.000000
vertices
1 2 1 0 /* el cuadrado contenido en la base del dominio fundamental */
2 1 1 0
3 1 2 0
4 2 2 0
5 0 1 2 /* el cuadrado contenido en la cara de detrás del dominio fundamental */
6 0 2 2
7 0 2 1
8 0 1 1
9 2 0 2 /* el cuadrado contenido en la cara de la izqda del dominio fundamental */
10 1 0 2
11 1 0 1
12 2 0 1
edges /* with torus wrap symbols */ Usamos los símbolos +.-,* para representar lados que salgan o entren en el dominio fundamental de T3
1 1 2 * * * /* el cuadrado contenido en la base del dominio fundamental */
2 2 3 * * *
3 3 4 * * *
4 4 1 * * *
5 5 6 * * * /* el cuadrado contenido en la cara de detrás del dominio fundamental */
6 6 7 * * *
7 7 8 * * *
8 8 5 * * *
9 9 10 * * * /* el cuadrado contenido en la cara de la izqda del dominio fundamental */
10 10 11 * * *
11 11 12 * * *
12 12 9 * * *
13 1 8 + * * /* los 4 cuadrados que unen el cuadrado de la base inferior con los laterales (solo 2 lados cada uno)*/
14 4 7 + * *
15 4 12 * + *
16 3 11 * + *
17 3 7 * * *
18 2 8 * * *
19 2 11 * * *
20 1 12 * * *
21 1 5 + * - /* los 4 cuadrados que unen el cuadrado de la base superior con los laterales (solo 2 lados cada uno)*/
22 4 6 + * -
23 4 9 * + -
24 3 10 * + -
25 3 6 * * -
26 2 5 * * -
27 2 10 * * -
28 1 9 * * -
29 7 12 - + * /* cerrar triangulos abajo */
30 11 7 * - *
31 8 11 * * *
32 12 8 + * *
33 6 9 - + * /* cerrar triangulos arriba */
34 10 6 * - *
35 5 10 * * *
36 9 5 + * *
faces
1 7 -13 -4 14 /* los 4 cuadrados que unen el cuadrado de la base inferior con los laterales */ Nótese que los cuadrados sobre las caras del cubo NO son caras de la configuración
2 -3 16 11 -15
3 -7 -17 -2 18 /* -7 18 -2 -17 */
4 -11 -19 -1 20
5 15 -29 -14 /* los 4 triangulos de abajo */
6 17 -30 -16
7 19 -31 -18
8 13 -32 -20
9 21 5 -22 4 /* los 4 cuadrados que unen el cuadrado de la base superior con los laterales */
10 23 9 -24 3
11 2 25 -5 -26
12 1 27 -9 -28
13 22 33 -23 /* los 4 triangulos de arriba */
14 24 34 -25
15 26 35 -27
16 28 36 -21
17 -33 6 29 12 /* los 4 cuadrados centrales */
18 -34 10 30 -6
19 -35 -8 31 -10
20 -36 -12 32 8
bodies
1 1 5 2 6 7 3 8 4 17 18 19 20 9 10 11 12 13 14 15 16 volume 13.500 Imponemos que el volumen del "dominio interior" sea la mitad del volumen de T3
read
Si tecleamos v, veremos que el volumen real inicial del "dominio interior" es 14.3333333333. Hay que evolucionar con cuidado el fichero anterior si queremos converger a la P-Schwarz. Esto puede hacerse controlando que el volumen del "dominio interior vaya aproximándose al valor impuesto, 13.5. Una secuencia de comandos que hace esto es
r
g
r
g
r
g
r
g
r
g
tras la cual el valor del volumen es 13.54683. El gráfico mostrará una superficie casi negra, porque la triangulación está muy refinada. Para aclarar el gráfico, teclearemos e.
Cuando usamos Evolver sobre un toro 2D o 3D, a cada vector generador del retículo se le asocia automáticamente una transformación como vimos en el tema "Simetrías". Por ejemplo, tecleando sobre la ventana de comandos donde teníamos la evolución de schwarz1.fe lo siguiente
transform_expr "abc"
obtendremos $2\times 2\times 2$ veces la configuración anterior.
Otro ejemplo de configuración en un toro 3D: el empaquetamiento de Lord Kelvin.
Lord Kelvin conjeturó en el siglo XIX que la forma más eficiente de subdividir el espacio en regiones de igual volumen (más eficiente significa de menor área por unidad de volumen) consistía en usar poliedros de 14 caras, de ellas 6 cuadrados y 8 hexágonos regulares, como en la figura de abajo. Esta configuración vive en el toro cúbico estándar $\mathbb{T}^3$. El fichero twointor.fe implementa dos celdas del empaquetamiento de Lord Kelvin en un dominio fundamental de $\mathbb{T}^3$.
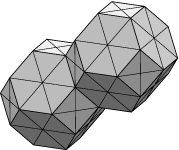
A continuación transcribimos el fichero twointor.fe insertando comentarios.
2 0.25 0.00 0.50
3 0.00 0.25 0.50
4 0.75 0.00 0.50
5 0.00 0.50 0.75
6 0.50 0.00 0.25
7 0.00 0.75 0.50
8 0.50 0.25 0.00
9 0.25 0.50 0.00
10 0.00 0.50 0.25
11 0.50 0.75 0.00
12 0.75 0.50 0.00
edges /* with torus wrap symbols */
1 1 2 * * * 2 2 3 * * *
3 1 4 * * *
4 3 5 * * *
5 2 6 * * *
6 2 7 * - *
7 1 8 * * +
8 4 6 * * *
9 5 9 * * +
10 3 10 * * *
11 3 4 - * *
12 6 8 * * *
13 6 11 * - *
14 7 4 - + *
15 8 12 * * *
16 9 8 * * *
17 9 11 * * *
18 10 7 * * *
19 11 1 * + -
20 12 5 + * -
21 5 7 * * *
22 11 12 * * *
23 10 12 - * *
24 9 10 * * *
faces
1 1 2 4 9 16 -7 Las caras 3,5,6,8,9 y 13 corresponden a los 6
cuadrados del poliedro. El resto son los hexágonos.
2 -2 5 12 -16 24 -10 3 -4 10 18 -21 4 7 15 20 -4 11 -3 5 -1 3 8 -5 6 6
14 -11 -2 7 5 13 -17 24 18 -6 8 -12 13 19 7 9 -16 17 22 -15 10 -10 11 8
12 15 -23 11 -21 9 17 19 1 6 12 -14 -18 23 -22 -13 -8 13 -24 -9 -20 -23
14 -19 22 20 21 14 -3 bodies
1 -1 -2 -3 -4 -5 9 7 11 -9 10 12 5 14 3 volume 0.500 Tenemos
dos cuerpos delimitados por sendos poliedros de Lord Kelvin. Asignamos
a cada uno el volumen mitad del volumen total.
2 2 -6 -7 8 -10 -12 -11 -13 1 13 -14 6 4 -8 volume 0.500
read
// Typical evolution
gogo := { g 5; r; g 5; hessian; r; g 5; hessian; hessian; }Si evolucionamos la configuración anterior (usar por ejemplo la evolución indicada al final del fichero), veremos que Evolver modifica la configuración inicial hacia otra con lados y caras ligeramente curvados. Esto nos dice que ni siquiera dentro de los empaquetamientos con la misma combinatoria de la de Lord Kelvin, ésta hace un mínimo del área por unidad de volumen.
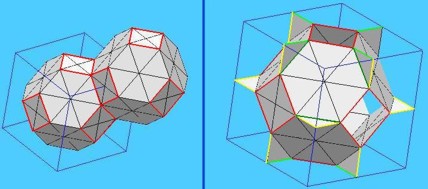
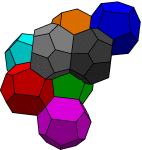
Nota. Existen empaquetamientos por poliedros (caras poligonales, sin curvatura) con distinta combinatoria que el empaquetamiento de Lord Kelvin y que mejoran la razón de área consumida por unidad de volumen. Esto ocurre con el empaquetamiento de Weiare-Phelan, contenido en el fichero phelanc.fe. Este empaquetamiento consta de 8 cuerpos por dominio fundamental, de los cuales 2 son dodecaedros regulares (verde y azul) y los otros 6 son poliedros no regulares cuyas caras son 12 pentágonos y 2 hexágonos. De nuevo iterando se comprueba que tampoco esta configuración es la mejor posible.
Ejercicios
1. Aplicar los principios de reflexión de Schwarz para reflejar con Evolver la superficie obtenida en el apartado 1 del ejercicio 1 del Tutorial 4 respecto de sus lados frontera.
2. Aplicar los principios de reflexión de Schwarz para reflejar con Evolver la solución del problema de Gergonne (Tutorial 6), simetrizándola hasta obtener una superficie triplemente periódica (esta última superficie también fue obtenida por Schwarz, a la que llamó la D de Schwarz).
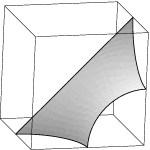
3. Crear una superficie mínima, con la topología de un disco, cuyo borde sea una diagonal que une los puntos medios de dos aristas opuestas de un cubo y tres arcos de frontera libre en tres caras adyacentes del cubo, como en la figura siguiente. Simetrizar esta superficie respecto a cada arco en su borde (tres reflexiones y una rotación de 180º) hasta producir una superficie mínima triplemente periódica.
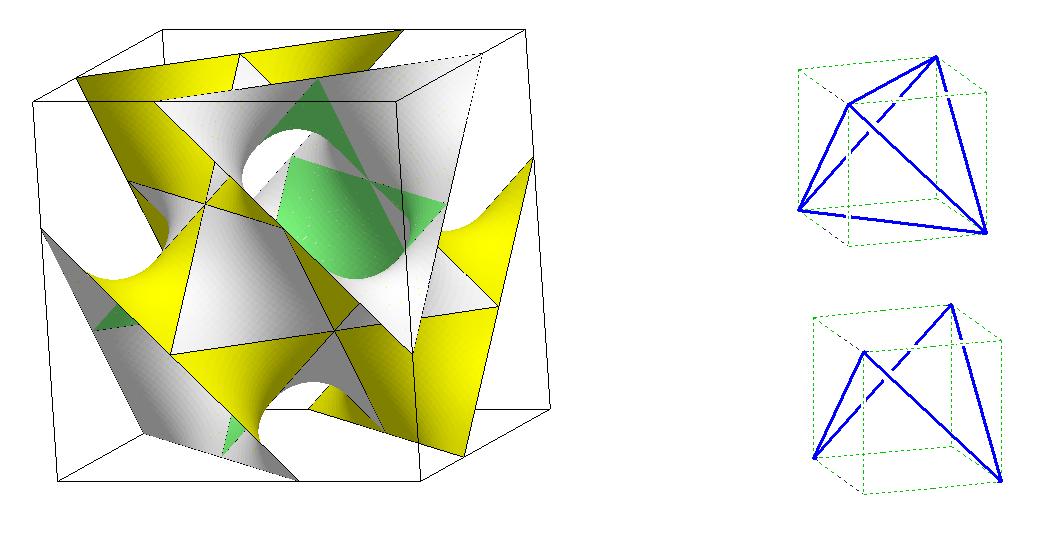
4. A continuación construiremos la superficie D de Schwarz de otra forma.
Tomemos un tetraedro regular inscrito en un cubo y eliminemos un par de aristas opuestas
(como en la figura de la derecha), obteniendo así un cuadrilátero. Si resolvemos
el problema de Plateau asociado a este cuadrillátero como borde, y reflejamos el resultado
reiteradamente usando los principios de reflexión de Schwarz, obtendremos una superficie periódica infinita,
que es la superficie D de Schwarz. Implementar este proceso con Evolver, de forma que la superficie
obtenida sea exactamente la figura de la izquierda. En particular, notemos que debemos resolver con Evolver
dos problemas de Plateau porque en cuadriláteros adyacentes, los colores de la superficie son distintos
(amarillo-blanco y blanco-verde).
5. Utilizando Evolver, construir la superficie mínima
periódica C(P), tambien llamada superficie de Neovius. La
superficie C(P) contiene las mismas rectas que la superficie D de
Schwarz. Además, ambas superficies tienen las mismas simetrías. Para
construirla, siguiendo la figura adjunta, tenemos que construir un
octógono resolviendo un problema de Plateau con frontera fija y un
cuadrilátero resolviendo otro problema de Plateau con frontera en parte
fija y en parte libre. Por último usaremos las simetrías para obtener
toda la superficie.
