Estás en: Página de docencia de Javier Pérez > Apuntes
Las Matemáticas se escriben con 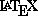
Hay varios sitios en Internet que son muy conocidos porque en ellos se ofrecen a los estudiantes apuntes de clase sobre las materias más diversas. Es tanta la oferta que no es fácil elegir. Afortunadamente, para unos apuntes de matemáticas hay un primer criterio elemental de calidad: que estén escritos con 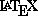 . El lenguaje
. El lenguaje 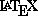 se creó para producir textos científicos, especialmente matemáticos, de gran calidad tipográfica. Hoy día, el uso de dicho lenguaje se ha generalizado en toda la comunidad científica hasta el punto de que si bien hace algunos años podía ser excusable, por su novedad, que un científico no lo usara, ya no lo es. Los apuntes que hay aquí están, por supuesto, escritos con
se creó para producir textos científicos, especialmente matemáticos, de gran calidad tipográfica. Hoy día, el uso de dicho lenguaje se ha generalizado en toda la comunidad científica hasta el punto de que si bien hace algunos años podía ser excusable, por su novedad, que un científico no lo usara, ya no lo es. Los apuntes que hay aquí están, por supuesto, escritos con 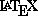 . Se trata de un lenguaje de etiquetas con el que es inevitable cometer alguna que otra errata. Te agradecería que las que encuentres me las comuniques por e-mail
. Se trata de un lenguaje de etiquetas con el que es inevitable cometer alguna que otra errata. Te agradecería que las que encuentres me las comuniques por e-mail ![]() .
.
En la página Docencia con Mathematica hay más apuntes en el formato propio de dicho programa.
Cálculo diferencial e integral de funciones de una variable. Con 270 ejercicios resueltos y notas históricas 
Los estudiantes se quejan, con razón, del excesivo rigor lógico deductivo y del formalismo matemático de muchos textos de introducción al Cálculo diferencial e integral, que parecen escritos más para profesores que ya conocen la materia que para estudiantes que se inician en ella. Sin ignorar que la deducción lógica y el lenguaje matemático tienen unas exigencias mínimas que hay que respetar, he procurado usar en todo momento un estilo bastante informal. Este libro está escrito un poco igual que se explica en clase delante de la pizarra, me he puesto en el lugar de un hipotético estudiante medio algo despistado y me hago eco de sus presumibles dudas, preguntas y confusiones, e intento explicar esas dudas, responder a las preguntas y aclarar las confusiones. Mi propósito ha sido exponer los conceptos con claridad, justificar la necesidad de herramientas de cálculo como las derivadas o las integrales para resolver una gran variedad de problemas y comprobar con ejemplos que dichas herramientas son realmente eficaces y útiles. Más que demostrar los teoremas, se trata de aprender a usarlos y entender su significado.
Con frecuencia los estudiantes tienen la idea de que las matemáticas son algo cerrado y acabado, un conjunto de verdades eternas e inmutables de una fría perfección que se transmiten dogmáticamente de generación en generación y donde no hay lugar para la sorpresa ni la pasión. Nada más lejos de la realidad, y para convencerse de ello nada mejor que dar un repaso a la historia de las matemáticas. Por esa razón he concedido toda la importancia que merece al desarrollo y evolución histórica de los principales conceptos del Cálculo. He incluido apuntes históricos, mucho más amplios de lo usual en textos de estas características, sobre la evolución de los conceptos de número y magnitud, límite y función, derivadas e integrales, así como sobre el infinito matemático y la algebraización del Análisis llevada a cabo en el último tercio del siglo XIX. Mi propósito al escribirlas ha sido presentar la génesis de los conceptos matemáticos en su contexto, su titubeante y confusa evolución, las discrepancias sobre el significado de los mismos... En una palabra, proporcionar al estudiante una visión de la matemática viva.
Mi intención ha sido escribir un libro de Cálculo que sea útil tanto para el futuro matemático como para el futuro ingeniero, pero cada uno debe leer el libro de la forma adecuada a sus intereses y necesidades. Para ambos será de gran utilidad la colección de ejercicios propuestos y también resueltos que se incluye, muchísimo más amplia de lo que suele ser usual en un libro de texto.
El contenido no ofrece sorpresa alguna y responde a un acuerdo general tácito de lo que debe constituir un curso básico de Cálculo de funciones de una variable. Una síntesis del mismo se expone seguidamente.
- Números reales y complejos.
- Funciones elementales.
- Continuidad y límite funcional.
- Derivadas. Aplicaciones de las derivadas.
- Sucesiones numéricas.
- Integral de Riemann. Aplicaciones de la integral.
- Series numéricas.
- Sucesiones y series de funciones.
Cálculo diferencial de funciones de varias variables 
Se trata de un curso de cálculo diferencial en Rn en el que se incluye la teoría básica de espacios métricos y espacios normados de dimensión finita. Su contenido es el tradicional en este tipo de cursos y está pensado para ser impartido en un cuatrimestre. Quizás la pequeña novedad consiste en que soy coherente con el hecho de que trabajo en dimensión finita: nada de teoremas propios de espacios de Banach como el teorema del punto fijo o el lema de Schnauder y cosas así. Uso la compacidad. También evito el uso de la diferencial segunda y sucesivas para campos vectoriales pues con derivadas parciales se trabaja más cómodamente. He incluido solamente las demostraciones de aquelllos resultados que a mi juicio ofrecen alguna dificultad. En particular, las demostraciones de los teoremas de la función inversa e implícita y sus consecuencias están hechas con más detalle de lo que es habitual. También he incluido una amplia colección de ejercicios.
- El espacio euclídeo Rn. Espacios métricos y espacios normados.
- Topología de un espacio métrico. Convergencia en espacios métricos. Continuidad.
- Espacios normados de dimensión finita. Teoremas de Hausdorff y de Bolzano-Weierstrass.
- Derivadas parciales.
- Vector gradiente. Campos escalares diferenciables.
- Extremos relativos.
- Funciones vectoriales diferenciables. Matriz jacobiana.
- Teoremas de la función inversa e implícita.
- Variedades diferenciables en Rn.
- Extremos condicionados.
Cálculo vectorial. Series de Fourier. Teorema de los residuos 
Los resultados clásicos del Cálculo vectorial, especialmente los teoremas de Green, de Stokes y el teorema de la divergencia de Gauss, son herramientas imprescindibles en varias ramas de la Física, particularmente en Electromagnetismo e Hidrodinámica. Para un matemático, el contexto natural donde situar estos resultados es la teoría de la integración en variedades diferenciables, donde dichos teoremas clásicos pueden verse como casos particulares de un resultado más general. El precio que hay que pagar para alcanzar este nivel de generalidad es muy alto pues la teoría de variedades diferenciables es muy técnica. Un matemático debe conocerla, un ingeniero no tiene por qué. Para eludir esta dificultad es fácil caer en el otro extremo y olvidarse de toda exigencia de rigor. Con el teorema de los residuos sucede algo parecido; para eludir las precisiones topológicas necesarias se cae en enunciados muy particulares cuando no incorrectos. Mi objetivo en estos apuntes ha sido exponer con claridad los conceptos y resultados principales del cálculo vectorial clásico y de la integración compleja, sin eludir las dificultades inherentes a los mismos y proponiendo soluciones matemáticamente correctas y elementales. La parte dedicada a series de Fourier es muy básica y elemental. En conjunto, se trata de un curso básico apropiado para estudiantes de los dos primeros años de Escuelas Técnicas Superiores. También puede ser útil para estudiantes de la Licenciatura de Físicas. Su contenido es el siguiente.
- El espacio euclídeo Rn. Curvas en Rn. Velocidad, rapidez, aceleración.
- Integrales de línea de campos escalares y vectoriales.
- Campos conservativos. Teorema de Green.
- Rotacional y divergencia.
- Coordenadas curvilíneas ortogonales. Coordenadas polares, cilíndricas y esféricas.
- Superficies. Integrales de superficie de campos escalares y vectoriales.
- Teorema de Stokes y teorema de Gauss o de la divergencia.
- Aplicaciones. Ecuación de continuidad de la hidrodinámica. La ley de Gauss y la ecuación de Poisson en electrostática.
- Polinomios trigonométricos y coeficientes de Fourier.
- Geometría de las series de Fourier.
- Introducción a la Transformada de Fourier Discreta.
- Transformada de Fourier.
- Convolución y sistemas LTI.
- Integración de funciones complejas. El teorema de los residuos y sus aplicaciones.
En la página Docencia con Mathematica he puesto el curso de Cálculo Vectorial en formato de cuadernos de Mathematica lo que permite visualizar muchos conceptos de contenido geométrico y hacer con comodidad cálculos que a veces son un poco largos para hacerlos manualmente.
Complementos de Cálculo 
Las circunstancias particulares, que no vienen al caso, del curso para el que inicialmente escribí estos apuntes explican sus muchas carencias. Pese a ello, finalmente he decidido dejarlo aquí en la confianza de que quizás puede serle útil a alguien. Además, en la página Prácticas con Mathematica se tratan temas de ecuaciones diferenciales, como el oscilador armónico y algo de dinámica de poblaciones, para los que este texto sirve de referencia. Su contenido es el siguiente.
- Repaso de la exponencial compleja.
- Métodos de resolución de ecuaciones diferenciales ordinarias.
- Ecuación diferencial lineal y sistemas de ecuaciones diferenciales lineales.
- Funciones analíticas de una matriz cuadrada.
- Aplicaciones. Oscilaciones libres y forzadas. Circuitos eléctricos RLC. Sistemas LTI.
- Transformada de Laplace.
- Conceptos básicos de la teoría de series y transformada de Fourier.
Funciones de variable compleja 
Este texto está escrito cuidando un poco más los aspectos formales y lógico-deductivos. Se trata de un curso tradicional de introducción a la teoría de funciones de una variable compleja. He dedicado especial atención al estudio de las funciones elementales complejas pues son pocos los textos que se detienen en ellas, y muy en particular al estudio de los logaritmos complejos. También creo que la notación empleada para representar las funciones elementales, cuestión básica en la que lamentablemente los textos no se ponen de acuerdo, es clara y coherente. El libro contienen más de de 300 ejercicios y algunos de ellos están resueltos. Su contenido es el siguiente.
- Números complejos y funciones complejas elementales.
- Series de potencias y funciones analíticas.
- Integración en el campo complejo. Teoría de Cauchy elemental.
- Propiedades locales de las funciones holomorfas.
- El problema de Dirichlet para discos.
- Forma general del teorema de Cauchy.
- Series de Laurent. Singularidades. Cálculo de residuos.
- El teorema de los residuos y sus aplicaciones.
- Representación conforme.
- El teorema de Riemann de la representación conforme.
- Diversas caracterizaciones de los dominios simplemente conexos del plano.
Análisis Funcional en Espacios de Banach 
Este libro, dirigido a estudiantes del Grado en Matemáticas o Física, es una introducción al Análisis Funcional en el ambiente de los espacios de Banach. Es un texto esencialmente autosuficiente en el que la teoría, con demostraciones incluidas, se desarrolla progresivamente desde los conceptos más básicos hasta los resultados fundamentales de la teoría de los espacios de Banach. Su lectura presupone conocimientos básicos de álgebra lineal, topología de espacios métricos, cálculo diferencial y la integral de Lebesgue.
El libro consta de 10 capítulos y cada uno de ellos lleva una introducción en la que se indican los objetivos del mismo y los principales resultados. Cada capítulo termina con una amplia colección de ejercicios cuyo grado de dificultad he procurado mantener en un nivel medio. Su contenido es el siguiente
- Espacios normados. Conceptos básicos.
- Ejemplos de espacios normados.
- Operadores y funcionales lineales continuos.
- Espacios normados de dimensión finita. Espacio normado cociente. Sumas topológico-directas.
- Espacios de Hilbert.
- Operadores en espacios de Hilbert.
- Teorema de Hahn-Banach.
- Dualidad en espacio normados.
- Principio de acotación uniforme. Teorema de la aplicación abierta.
- Topologías débiles.
Conceptos Básicos de Análisis Real 
Se trata de un texto escrito para la asignatura Cálculo I de primer curso del doble Grado en Ingeniería Informática y Matemáticas de la Universidad de Granada. En el Prólogo escribo, dirigiéndome a un hipotético estudiante:
En esta asignatura vas a estudiar algunos de los conceptos fundamentales del Análisis Matemático. Su nombre, ``Cálculo I'', es muy desafortunado porque nada tiene que ver con las técnicas usuales del Cálculo: derivadas, integrales o ecuaciones diferenciales. Aquí vas a estudiar conceptos muy básicos pero imprescindibles porque ellos proporcionan los fundamentos para desarrollar dichas técnicas. Debes saber que esos conceptos no son necesarios para las aplicaciones prácticas del Cálculo. De hecho, no forman parte de la formación de los ingenieros. Para resolver problemas prácticos aplicando técnicas de cálculo diferencial o integral solamente es preciso conocer dichas técnicas y saber aplicarlas a situaciones concretas, no es necesario comprender sus fundamentos. Pero la formación de un matemático, y tú estás leyendo esto porque quieres serlo, tiene que incluir de forma destacada el estudio de los mismos. El Cálculo con fundamentos se llama Análisis Matemático. Los ingenieros estudian Cálculo, los matemáticos estudiamos Análisis Matemático. Lo principal en esta asignatura no son las técnicas sino los conceptos. Sucede que los conceptos más básicos son los más abstractos y por eso esta es una asignatura difícil.
Su contenido es el siguiente:
- Números reales. Conjuntos infinitos y conjuntos numerables.
- Sucesiones convergentes. Logaritmos y exponenciales.
- Sucesiones parciales y valores de adherencia. Sucesiones divergentes.
- Series de números reales. Crtiterios de convergencia para series de términos positivos.
- Series conmutativamente convergentes. Convergencia absoluta.
- Funciones reales continuas. Teorema de Bolzano.
- Continuidad y monotonía. Continuidad en intervalos cerrados y acotados.
- Límite funcional. Límites de funciones monótonas.
Puedes descargar las diapositivas con las presentaciones de todos los temas en un archivo comprimido  .
.
Aquí tienes algunos ejercicios de este curso  .
.
Análisis Matemático para primer curso del Grado en Biotecnología
Durante varios años he impartido la asignatura Análisis Matemático a estudiantes de primer curso del Grado en Biotecnología de la Universidad de Granada. He procurado adaptar la asignatura dedicando especial atención a aquellos temas que pueden ser más interesantes para los estudiantes de dicho Grado.
He dividido el programa en los siguientes temas.
- Tema 1. Matrices y sistemas de ecuaciones lineales.
- Tema 2. Aplicaciones del cálculo matricial.
- Tema 3. Funciones reales.
- Tema 4. Continuidad. Límites. Derivadas.
- Tema 5. Integrales.
- Tema 6. Ecuaciones diferenciales y dinámica de poblaciones.
- Tema 7. Funciones de varias variables.
- Tema 8. Integrales múltiples.
Puedes descargar las diapositivas con las presentaciones de todos los temas en un archivo comprimido  .
.
Aquí tienes las relaciones de ejercicios de este curso  .
.
Evolución histórica de los conceptos básicos del Análisis Matemático 
- Números y cantidades. El continuo y lo discreto.
- Evolución del concepto de función y límite funcional.
- Orígenes y desarrollo del concepto de derivada. La invención del Cálculo.
- Evolución de la idea de integral.
- El Cálculo y las series.
- Breve historia del infinito.
- Los orígenes del Análisis Funcional.
Útima actualización: 23/04/2019

