Historia del concepto de grupo.

El estudio del desarrollo del concepto de grupo tiene ciertas peculiaridades. Es erróneo pensar que puesto que los racionales, distintos de cero Q*=Q-{0}, forman grupo respecto de la multiplicación. Entonces, éstos son el origen del concepto y que por tanto debe ser tan antiguo como ellos mismos, remontándose al inicio de las matemáticas.

Sin embargo, no fue así, el concepto de grupo es un ejemplo de como la abstracción de algunas ideas, comunes a muchas áreas de la matemática, que se iban desarrollando paralelamente, han necesitado de la distancia y del tiempo para poder asentarse, y dar lugar a una definición que satisfaciera formalmente y diera cabida a todos los ejemplos. Ésto no sucedió plenamente hasta el siglo XX. Pudiéndose decir que la teoría de grupos, aunque tuvo resultados importantes anteriores, es una teoría moderna en la historia de la matemática. Aunque ya en pleno siglo XXI, se puede decir que está plenamente consolidada como disciplina matemática y convertida en un clásico en el curriculum académico.

Las tres áreas en las que surgió, de forma natural e implícitamente, el concepto de grupo son: en la geometría al comienzo del siglo XIX, en la teoría de números al final del siglo XVIII y en la teoría de ecuaciones algebráicas al final también del dieciocho y que condujo al estudio de las permutaciones.

La geometría habia sido estudiada desde el tiempo de los griegos, siendo la primera teoría en formularse formalmente y el paradigma de todas las teorías matemáticas. ¿Que pasó al principio del diecinueve?. Había empezado a perder su caracter métrico, con la geometría proyectiva y las geometrías no euclidianas. El estudio de la geometría en n dimensiones condujo a una abstracción en la geometría misma. La diferenciación entre la geometría métrica y la geometría incidental empezó a gestarse con el trabajo de Monge, su alumno Carnot y más aún con Poncelet. Las geometrías no euclidianas fueron estudiadas por Lambert, Gauss, Lobachevsky y János Bolyai entre otros. Möbius en 1827, aunque sin percatarse del concepto de grupo, empezó a clasificar geometrías según propiedades que permanecen invariantes bajo un determinado grupo de transformaciones. Steiner en 1832, estudió nociones de geometría sintética que pueden formar parte del estudio de ciertos grupos de transformaciones.

En 1761, Euler estudió la aritmética modular. En particular, analizó los restos módulo n, de potencias de un número. Aunque el trabajo de Euler no lo estableció en términos de teoría de grupos, él dió un ejemplo de descomposición de un grupo abeliano finito en clases adjuntas, según un subgrupo y probó un caso especial del resultado (hoy conocido como teorema de Lagrange): el orden de un subgrupo divide al orden del grupo. Gauss, en 1801, llevó el teorema de Euler mucho mas allá y probó resultados de aritmética modular que son especializaciones de teoremas generales de grupos abelianos. Estudió el orden de los elementos y probó que (aunque no con esta notación) que existe un subgrupo para cada divisor del orden de un grupo cíclico. Gauss también examinó otros grupos abelianos. Analizó las formas cuadráticas binarias, con coeficientes enteros, y las estudió bajo transformaciones y sustituciones. Las clasificó en clases de equivalencia y definió un producto de clases. Gauss probó que el orden del producto (de 3 formas) es immaterial; en nuestro lenguaje actual probó la propiedad asociativa del producto de clases. De hecho, Gauss obtuvo un grupo abeliano finito. Más tarde, en 1869, Schering que editó el trabajo de Gauss, encontró un sistema de generadores para este grupo abeliano.

El primero que estudió las permutaciones fue Lagrange en 1770, en su trabajo sobre teoría de ecuaciones algebráicas. El objetivo de Lagrange era encontrar los motivos por los que las ecuaciones de tercer y cuarto grado son resolubles por radicales. Al estudiar la cúbica general, encontró que ciertas combinaciones de sus raíces (hoy llamadas resolventes de Lagrange) tomaban solo tres valores bajo las seis permutaciones de sus tres raíces. Este trabajo se considera el origen de los grupos de permutaciones. Aunque, en honor de la verdad Lagrange nunca consideró el producto de dos permutaciones; o sea, su estructura de grupo.

La primera persona que afirmó que la quíntica podía no ser resoluble por radicales fue Ruffini. En 1799, publicó dicha irresolubilidad algebráica (de las ecuaciones de quinto grado) en un trabajo erróneo. En este trabajo, basado en el de Lagrange, Ruffini introduce los grupos de permutaciones. Los llama permutazione y únicamente describe la propiedad de clausura de la composición, manejando la propiedad asociativa de forma implícita (al ser una composición de aplicaciones). Ruffini divide sus permutazione en tipos. En notación moderna, distingue grupos de permutaciones cíclicos (permutazione semplice) y no cíclicos (permutazione composta). Las permutazione composta las divide en tres, que en nuestra notación son los grupos intransitivos de permutaciones y los transitivos primitivos y no primitivos. Desgraciadamente, la demostración de Ruffini tenía dos saltos lógicos que no logró salvar en posteriores publicaciones. De todas formas, en 1802, mostró que el grupo de permutaciones asociado a una ecuación irreducible es un subgrupo transitivo (hoy día sabemos que el recíproco es cierto), llevando el estudio de las permutaciones a un estado muy avanzado para su época.

El trabajo de Cauchy fue muy importante en la teoría de permutaciones. En 1815, estudia las permutaciones de las raíces de ecuaciones. Pero, en 1844, Cauchy estudia las permutaciones por sí mismas. Introduce la notación de potencias positivas o nevativas (incluída la potencia 0 definiéndola como la permutación identidad), define el orden de una permutación, introduce la notación de ciclo actual y usa el término de sutituciones conjugadas. Cauchy llama a dos permutaciones similares si tienen la misma descomposición en ciclos disjuntos y demuestra que es equivalente a ser permutaciones conjugadas.

Abel, en 1824, dió la primera prueba aceptada de la irresolubilidad de la quíntica general. En términos modernos, probó que el grupo alternado (de las permutaciones pares) de cinco símbolos, A5, es un grupo simple y que en consecuencia el grupo de todas las permutaciones de 5 símbolos, S5, es no resoluble.

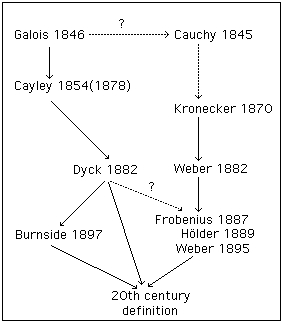
Galois, en 1831, fue el primero en darse cuenta de que la solución algebráica de una ecuación estaba relacionada con la estructura de un grupo de permutaciones asociado a la ecuación (llamado hoy, en su honor, el grupo de Galois de la ecuación). En 1832, Galois había descubierto que ciertos subgrupos, hoy llamados subgrupos normales, eran fundamentales en su demostración. Llamó descomposición propia a la descomposición en clases adjuntas, si coinciden por la izquierda y por la derecha. Galois también mostró que el primer grupo simple no abeliano tenía orden 60 (el alternado A5 de Abel). Sin embargo, el trabajo de Galois no se publicó hasta 1846. Liouville lo hizo publicar, al encontrar conexiones entre la teoría de permutaciones de Cauchy y la de Galois. Sin embargo, Liouville no entendió la importancia del concepto de grupo en el trabajo de Galois.

Betti, en 1851, relacionó la teoría de permutaciones y la teoría de ecuaciones. De hecho, Betti fue el primero en probar que el grupo de Galois asociado a una ecuación era de hecho un grupo de permutaciones en el sentido moderno. Serret publicó un importante trabajo discutiendo el artículo de Galois, publicado por Liouville, todavía sin resaltar la significación del concepto de grupo. Sin embargo, Jordan, primero en 1865 y 1869 de forma parcial y finalmente en 1870 (40 años después) entendió cláramente la importancia de los grupos de permutaciones. Definió isomorfismo de grupos de permutaciones y probó el teorema (llamado hoy de Jordan-Hölder) de existencia y unicidad, salvo isomorfía, de series de composición para estos grupos. Hölder lo generalizó al contexto de grupos abstractos en 1889.

En 1872, Klein expuso su objetivo (hoy conocido como programa de Erlangen) de clasificación de las geometrías según propiedades invariantes vía subgrupos de transformaciones. Por fin, los grupos se convierten en centro de atención para investigación en matemáticas.

Quizás el trabajo mas importante, anterior a Betti, en teoría de grupos sea debido a Cayley. En 1849, Cayley publicó un artículo relacionando sus ideas sobre permutaciones con las de Cauchy. En 1854, Cayley hace un intento de definición de grupo abstracto, que aunque no es todavía formalmente correcta, usa una tabla de multiplicación para describir la composición en un grupo finito. Significativamente se da cuenta de que los cuaternios y las matrices forman grupo. Cayley en 1878, escribió 4 artículos sobre el tema, uno de ellos llamado The theory of groups. La época estaba madura para el estudio de un grupo arbitrario. Cayley demuestra que cualquier grupo finito puede describirse en términos de grupos de permutaciones.

Esto impulsó a Hölder, en 1893, a investigar los grupos de orden p3, pq2, pqr and p4. Frobenius y Netto (un estudiante de Kronecker) llevaron la teoría de grupos un poco más allá. Sin embargo, la mayor contribución de finales del XIX la hizo von Dyck. Había obtenido su doctorado bajo la supervisión de Klein y era su ayudante. En 1882 y 1883, von Dyck dió una contrucción de los grupos libres y una definición de grupo dado por generadores y relaciones.

La teoría de grupos tuvo mayoría de edad cuando se publicaron los libros, primero los dos tomos de álgebra, Lehrbuch der Algebra en 1895, de Heinrich Weber (un estudiante de Dedekind) y el libro de Burnside, Theory of groups of finite order, publicado en 1897. Estos libros influenciaron a la siguiente generación de matemáticos e impulsaron el importante desarrollo que tuvo la teoría de grupos en el siglo XX.