5.3.3 Vida media biológica.

Cuando un isótopo es ingerido o inhalado, su concentración interna final dependerá del tiempo que es retenido por el cuerpo. La segunda y tercera columna de la tabla 10 proporcionan la información necesaria para estimar la retención efectiva. En la segunda columna aparece un parámetro que ya nos es familiar: la semi-vida del isótopo (denominado ``semi-vida radiactiva'' en la tabla). Para algunos isótopos la semi-vida es muy corta (por ejemplo, 0.63 d para el $^{24}$Na). Por tanto, tras ser ingerido, la concentración de este isótopo decaerá a niveles muy bajos tras varios dıas aunque no sea eliminado por el organismo. No obstante, la semi-vida de otros isótopos es de miles de dıas hasta miles de años. Desde nuestro punto de vista, tales isótopos son prácticamente permanentes y su concentración en el organismo se reduce principalmente por eliminación biológica.

La eliminación de un isótopo por medios biológicos puede expresarse en términos de una ``vida media biológica'', definida de forma similar a la vida media radiactiva. Esto es ası porque los procesos de transporte biológicos para un material dado son aproximadamente proporcionales a su concentración. Si $Q(t)$ es la concentración de cierta sustancia $Q$ en el organismo, ésta disminuye a una velocidad proporcional a su concentración, es decir:

$$\frac{dQ(t)}{dt} = - \lambda_b Q(t),$$ (17)

donde $\lambda_b$ es una constante de deposición biológica. En ausencia de radiactividad, la concentración disminuye exponencialmente

$$Q(t)=Q(0)\exp(-\lambda_b t)$$ (18)

La semi-vida biológica se define, pues, como

$$T_b = \frac{\ln 2}{\lambda_b}$$ (19)

Este es el valor que aparece en la tercera columna de la tabla 10. Por ejemplo, para el tritio (que es usualmente ingerido con el agua) la semi-vida biológica es relativamente corta $\sim 2$ dıas. Para los elementos pesados, que tienden a concentrarse en los huesos, la semi-vida biológica es muy larga.

La tasa de eliminación de un isótopo radiactivo está determinada por una constante de desintegración total efectiva, $\lambda_T$, que tiene en cuenta ambos procesos (desintegración radiactiva y deposición biológica):

$$\lambda_T=\lambda+\lambda_b.$$ (20)

Supongamos que se ha ingerido un isótopo con actividad $A_0$ que se concentra en un órgano de masa $M$. La tasa de dosis efectiva que produce en dicho órgano en función del tiempo está dada entonces por

$$\frac{dH(t)}{dt} = \frac{q\xi}{M} A_0 {\rm e}^{-\lambda_T t}$$ (21)

La dosis efectiva producida en un tiempo $t_1$ se obtiene integrando la expresión anterior entre 0 y $t_1$

$$H = \int_0^{t_1} \frac{dH(t)}{dt}dt = \frac{q\xi A_0}{M\lambda_T}\left( 1- {\rm e}^{-\lambda_T t_1}\right)$$ (22)

Ejemplo Una persona ha estado inhalando aire conteniendo $^{131}$I durante tres horas. Estimar la dosis total de radiación que habrá recibido en el tiroides transcurridos 30 dıas y 1000 dıas. La concentración de I en el aire es de $2.5\times 10^{-10}\,\mbox{Ci}/\,\mbox{m}^3$. El tiroides de un adulto pesa aproximadamente 20 g, y la tasa normal de aire inspirado es de $0.835\,\mbox{m}^3/\,\mbox{h}$.
En la tabla 10 se da la semi-vida del $^{131}$I como 8.04 d y la semi-vida biológica es de 138 d. La constante desintegración efectiva es de

$$\lambda_T= \frac{\ln 2}{T}+\frac{\ln 2}{T_b} = \frac{0.693}{8.04\,\rm d}+\frac{0.693}{138\rm\, d} = 0.0912\rm\,d^{-1}.$$

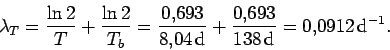
En la tabla también aparece el factor de energıa efectiva $\xi = 0.23 \,\mbox{MeV}$ y el factor de retención por inhalación de $q=0.23$ (la igualdad numérica de ambos números es casual).

La actividad total del isótopo inhalado durante las tres horas es de

$$\begin{eqnarray*} A_0 &=& 3 \,\mbox{h}\times 0.835 \,\mbox{m}^3/\,\mbox{h}\time... ...26 \times 10^{-10}\,\mbox{Ci}= 6.26 \times 10^{-4} \,{\rm\mu Ci} \end{eqnarray*}$$

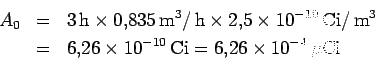
La dosis total recibida en el tiempo $t$ es de

$$H = \frac{q\xi A_0}{M\lambda_T}\left( 1- {\rm e}^{-\lambda_T t}\right)$$

Por tanto debemos calcular la dosis

$$\begin{eqnarray*} \frac{q\xi A_0}{M \lambda_T} &=& \frac{0.23\times 0.23 \,\m... ...=& 0.1816 \times 10^{-4} \frac{\rm MeV\,\mu Ci}{\rm g}\,\mbox{d} \end{eqnarray*}$$

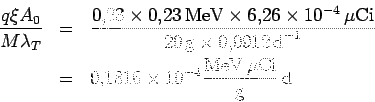
Ahora debemos transformar las unidades anteriores a unidades de dosis absorbida (rem). Veamos qué valor tiene lo siguiente:

$$\begin{eqnarray*} 1 \frac{\rm MeV\,\mu Ci}{\rm g} & = & \frac{1.602\times 10^{-... ...{\rm s} = 5.92 \times 10^{-4}\, {\rm rad/s} = 51.1 \,{\rm rad/d} \end{eqnarray*}$$

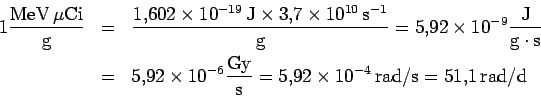
Por lo tanto, puesto que el factor de energıa efectivo $\xi$ ya incluye el factor de calidad, podemos escribir la dosis anterior directamente en rem:

$$\frac{q\xi A_0}{M \lambda_T} = 0.1816\times 10^{-4} \time... ...m} = 9.28 \times 10^{-4} \,\mbox{rem} = 0.928 \,\mbox{mrem}.$$

Para un tiempo de $t=30$ dıas se tiene

$$\exp(\lambda_T t) = \exp (-0.0912\times 30) = 0.0648$$

Por lo tanto, la dosis recibida tras 30 dıas será de

$$H(30\,\mbox{d})= 0.928\,\mbox{mrem}(1-0.0648) = 0.868 \,\mbox{mrem}$$

Tras 1000 dıas la exponencial es prácticamente cero, por lo que se ha alcanzado ya la dosis asintótica

$$H(1000\,\mbox{d}) = 0.928\,\mbox{mrem}.$$