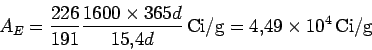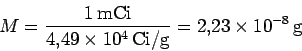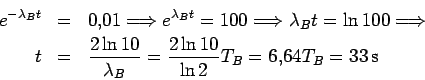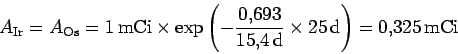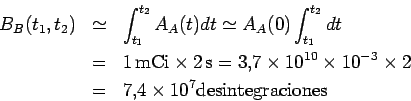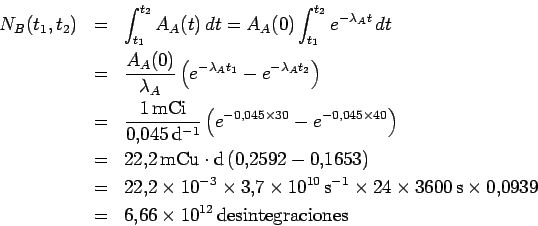

Next: 4 Propiedades estadísticas de
Up: 3.3 Equilibrios
Previous: 3.3.5 No equilibrio
 Os (15.4 d)
Os (15.4 d)
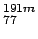 Ir (4.94s)
Ir (4.94s)
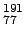 Ir
Ir
Se dispone de 1 mCi de 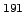 Os.
Os.
a) ¿Cuántos gramos de 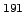 Os hay en
Os hay en 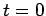 ?
?
b) ¿Cuántos mCi de 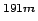 Ir hay en
Ir hay en 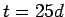 ?
?
c) ¿Cuantos átomos de 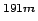 Ir se desintegran entre
Ir se desintegran entre 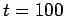 s y
s y
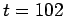 s?
s?
d) ¿Cuántos átomos de 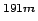 Ir se desintegran entre
Ir se desintegran entre 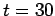 s y
s y
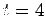 d?
d?
Solución.
- a)
Actividad específica del
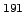 Os.
Os.
por tanto la masa de la muestra es
- b)
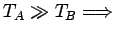 equilibrio secular en unos segundos.
equilibrio secular en unos segundos.
Las actividades difieren en un 1% cuando:
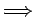 para
para 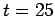 d:
d:
Usando la fórmula exacta se obtiene el mismo resultado
- c)
Sea
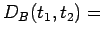 nº desintegraciones de átomos de
nº desintegraciones de átomos de 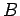 entre
entre 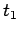 y
y 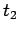 .
.
Para 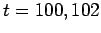 s se ha alcanzado el equilibrio secular
y la actividad del
s se ha alcanzado el equilibrio secular
y la actividad del 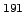 Os no habrá disminuido apreciablemente:
Os no habrá disminuido apreciablemente:
- d)
Entre
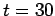 d y
d y 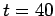 d la actividad del Os no es constante,
pero hay equilibrio secular:
d la actividad del Os no es constante,
pero hay equilibrio secular:


Next: 4 Propiedades estadísticas de
Up: 3.3 Equilibrios
Previous: 3.3.5 No equilibrio
J.E. Amaro
2006-05-05
![]() Os.
Os.
![]() Os hay en
Os hay en ![]() ?
?
![]() Ir hay en
Ir hay en ![]() ?
?
![]() Ir se desintegran entre
Ir se desintegran entre ![]() s y
s y
![]() s?
s?
![]() Ir se desintegran entre
Ir se desintegran entre ![]() s y
s y
![]() d?
d?