Loading [MathJax]/jax/output/HTML-CSS/config.js

Álgebra lineal con métodos elementales. Resolución de ejercicios tipo

Página Facebook: Álgebra lineal con métodos elementales.

Matriz asociada y cambio de base.

Recordemos que para determinar la matriz asociada a una aplicación lineal $f: V \longrightarrow V'$ respecto de bases $B$ de $V$ y $B'$ de $V'$ hemos de:
  1. Tomar los vectores de $B$.
  2. Aplicarles $f$.
  3. Tomar coordenadas respecto de $B'$.
  4. Ponerlos por columnas en una matriz.
Pero esto no siempre es cómodo y en particular si el calculo de coordenadas respecto de $B'$ es laborioso.

Consideremos la aplicación lineal $f:\mathbb{R}^3 \longrightarrow \mathbb{R}^2$ dada por $f(x,y,z) = (x+y,y-z)$ y calculemos la matriz asociada a $f$ respecto de las bases $\bar{B}=\{ (1,1,1), (1,1,0), (1,0,0)\}\;$ de $\mathbb{R}^3$ y $\bar{B'}=\{ (1,1), (1,0)\}$ de $\mathbb{R}^2$:

Primero aplicamos $f$ a los vectores de $\bar{B}$: $$ \begin{array}{l} f(1,1,1)=(2,0)\\ f(1,1,0)= (2,1) \\ f(1,0,0)=(1,0) \end{array} $$ Y ahora hemos de tomar coordenadas respecto de $\bar{B'}$, en este caso no es difícil ver que: $$ \begin{array}{l} (2,0)=(0,2)_{\bar{B'}}\\ (2,1)=(1,1)_{\bar{B'}} \\ (1,0)=(0,1)_{\bar{B'}} \end{array} $$

Luego la matriz buscada es: $$ C=\begin{pmatrix} 0 & 1 & 0\\ 2 & 1 & 1 \end{pmatrix} $$

Podemos ver como están relacionadas, en general, las matrices de una misma aplicación lineal respecto de distintas bases. Para ello, planteemos la situación:

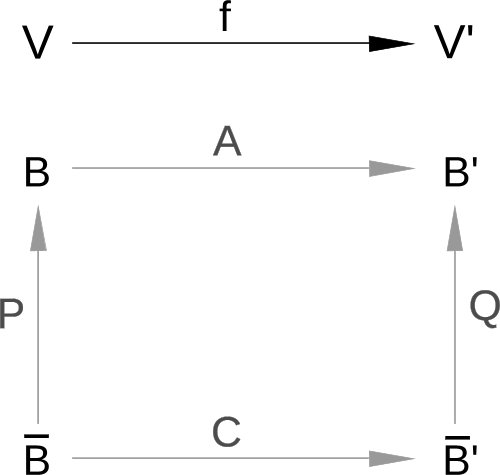
Sea $f: V \rightarrow V'$ una aplicación lineal y sean $B$ y $\bar{B}$ bases de $V$ y $B'$ y $\bar{B}'$ bases de $V'$. Por un lado podemos obtener $A=\mathfrak{M}_{B, B'}(f)$ y por otro $C=\mathfrak{M}_{\bar{B}, \bar{B'}}(f)$ ¿Qué relación existe entre $A$ y $C$?

Denotemos por $P$ la matriz del cambio de base de $\bar{B}$ a $B$ y por $Q$ la del cambio de base de $\bar{B}'$ a $B'$

Gráficamente tenemos la situación:

y las ecuaciones correspondientes son: $$ \begin{array}{cccl} Y &=&A·X, & \text{de $f$ respecto de $B$ y $B'$}\\ \bar{Y} &= &C · \bar{X}, & \text{de $f$ respecto de $\bar{B}$ y $\bar{B}'$}\\ X &= &P · \bar{X}, & \text{del cambio de $\bar{B}$ a $B$}\\ Y& = &Q · \bar{Y}, & \text{del cambio de $\bar{B}'$ a $B'$}\\ \end{array} $$ De las que se deduce fácilmente que la relación es: $$ C= Q^{-1}· A · P $$

Apliquemos lo visto al ejemplo anterior:

Denotamos por $B$ la base canónica de $\mathbb{R}^3$, la matriz del cambio de $\bar{B}$ es $$ P=\begin{pmatrix} 1 & 1 & 1 \\ 1 & 1 & 0 \\ 1 & 0 & 0 \end{pmatrix} $$ denotando por $B'$ la base canónica de $\mathbb{R}^2$, el cambio de $\bar{B}'$ a $B'$ viene dado por la matriz: $$ Q=\begin{pmatrix} 1 & 1 \\ 1 & 0 \end{pmatrix} $$ y la matriz de $f$ respecto de las bases canónicas es obviamente: $$ A= \begin{pmatrix} 1 & 1 & 0 \\ 0 & 1 & -1 \end{pmatrix} $$ así pues la matriz buscada es: $$ C=Q^{-1}· A · P=\begin{pmatrix} 0 & 1 & 0\\ 2 & 1 & 1 \end{pmatrix} $$

En el caso de los endomorfismos se toma la misma base en el espacio de partida y en el de llegada y por tanto será $P=Q$ y $C=P^{-1}·A·P$ ($A$ y $C$ son matrices semejantes).

Se considera la aplicación lineal $D: \mathcal{P}_3(\mathbb{R}) \longrightarrow \mathcal{P}_3(\mathbb{R})$ que a cada polinomio de $\mathcal{P}_3(\mathbb{R})$ le asigna su derivada: $D(p(x))=p'(x)$. Determinar la matriz asociada a $D$ respecto de la base $\bar{B}=\{ 1+x^2, x+x^3, 1+x^3, x^3\}$.

La matriz asociada a $D$ respecto de la base estándar es: $$ A= \begin{pmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & 2 & 0 \\ 0 & 0 & 0 & 3 \\ 0 & 0 & 0 & 0 \\ \end{pmatrix} $$ La matriz del cambio de base de $\bar{B}$ a $B$ se obtiene poniendo por columnas las coordenadas de los vectores de $\bar{B}$ respecto de $B$: $$ P= \begin{pmatrix} 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 1 & 1 \\ \end{pmatrix} $$ Por tanto la matriz buscada es: $$ C= P^{-1}·A·P= \begin{pmatrix} 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 1 & 0 & -1 & 0 \\ -1 & -1 & 1 & 1 \\ \end{pmatrix} · \begin{pmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & 2 & 0 \\ 0 & 0 & 0 & 3 \\ 0 & 0 & 0 & 0 \\ \end{pmatrix} · \begin{pmatrix} 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 1 & 1 \\ \end{pmatrix} = \begin{pmatrix} 0 & 3 & 3 & 3 \\ 2 & 0 & 0 & 0 \\ 0 & -2 & -3 & -3 \\ -2 & 2 & 3 & 3 \\ \end{pmatrix} $$ Por supuesto, podríamos haberlo hecho aplicando $D$ a los vectores de $\bar{B}$, calculando las coordenadas de los vectores obtenidos respecto de $\bar{B}$ y poniéndolos por columnas, pero calcular esas coordenadas es exactamente la tarea de calcular $P^{-1}$ con lo cual no se ahorra trabajo.

De una aplicación lineal $f:\mathbb{R}^3 \longrightarrow \mathbb{R}^4$ se sabe que: $$ \begin{array}{l} f(1,2,1)=(1,0,1,0)\\ f(2,1,2)= (0,1,0,1) \\ f(1,0,0)=(0,0,0,0) \end{array} $$ Determinar la matriz asociada a $f$ respecto de las respectivas bases canónicas de $\mathbb{R}^3$ y $\mathbb{R}^4$ y determinar $f(3,1,1)$.

Denotemos por $B$ y $B'$ las respectivas bases canónicas de $\mathbb{R}^3$ y $\mathbb{R}^4$ y consideremos en $\mathbb{R}^3$ la base $\bar{B}=\{ (1,2,1), (2,1,2), (1,0,0)\}$.

Con los datos que nos dan es fácil calcular la matriz $C$ asociada a $f$ respecto de $\bar{B}$ y $B'$, aplicamos $f$ a los vectores de $\bar{B}$ tomamos coordenadas respecto de $B'$ y los ponemos por columnas: $$ \begin{array}{l} f(1,2,1)=(1,0,1,0)=(1,0,1,0)_{B'}\\ f(2,1,2)= (0,1,0,1)=(0,1,0,1)_{B'} \\ f(1,0,0)=(0,0,0,0)=(0,0,0,0)_{B'} \end{array} $$ $$ C=\begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 1& 0 \end{pmatrix} $$

Por otro lado el cambio de base de $\bar{B}$ a $B$ viene dado por la matriz: $$ P=\begin{pmatrix} 1 & 2 & 1 \\ 2 & 1 & 0 \\ 1 & 2 & 0 \end{pmatrix} $$ En el segundo espacio $\mathbb{R}^4$ solo consideramos la base canónica $B'$ por lo que en este caso la matriz de cambio en el segundo espacio será la matriz identidad $Q=I$.

La relación entre la matriz $A$ asociada a $f$ respecto de las bases canónicas y la matriz $C$ obtenida será: $$ C= Q^{-1} · A · P = A · P $$ y despejando $A$ obtenemos que $$ A = C · P^{-1} $$ Calculamos: $$ A=\begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 1& 0 \end{pmatrix} · \begin{pmatrix} 1 & 2 & 1 \\ 2 & 1 & 0 \\ 1 & 2 & 0 \end{pmatrix}^{-1}= \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 1& 0 \end{pmatrix} · \begin{pmatrix} 0 & \frac{2}{3} & -\frac{1}{3} \\ 0 & -\frac{1}{3} & \frac{2}{3} \\ 1 & 0 & 0 \end{pmatrix} = \begin{pmatrix} 0 & \frac{2}{3} & -\frac{1}{3} \\ 0 & -\frac{1}{3}& \frac{2}{3} \\ 0 & \frac{2}{3} & -\frac{1}{3} \\ 0 & -\frac{1}{3}& \frac{2}{3} \\ \end{pmatrix} $$ Para obtener la imagen por $f$ del vector $(3,1,1)$ usamos la ecuación matricial de $f$ respecto de las bases canónicas: $$ \begin{pmatrix} y_1 \\ y_2 \\y_3 \\ y_4 \end{pmatrix} = \begin{pmatrix} 0 & \frac{2}{3} & -\frac{1}{3} \\ 0 & -\frac{1}{3}& \frac{2}{3} \\ 0 & \frac{2}{3} & -\frac{1}{3} \\ 0 & -\frac{1}{3}& \frac{2}{3} \\ \end{pmatrix} · \begin{pmatrix} x_1 \\ x_2 \\x_3 \end{pmatrix} $$ $$ \begin{pmatrix} 0 & \frac{2}{3} & -\frac{1}{3} \\ 0 & -\frac{1}{3}& \frac{2}{3} \\ 0 & \frac{2}{3} & -\frac{1}{3} \\ 0 & -\frac{1}{3}& \frac{2}{3} \\ \end{pmatrix} · \begin{pmatrix} 3 \\ 1 \\1 \end{pmatrix}= \begin{pmatrix} \frac{1}{3} \\ \frac{1}{3} \\ \frac{1}{3} \\ \frac{1}{3} \end{pmatrix} $$ $$ f(3,1,1)= (\frac{1}{3},\frac{1}{3},\frac{1}{3}, \frac{1}{3}) $$