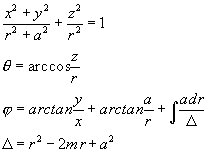 (1)
(1)
EL ESPACIO-TIEMPO COMPLETO DE KERR COMO BASE DE UN MODELO GEOMETRICO DE LA REALIDAD FISICA.
1 Introducción.
La Física ortodoxa actual asume en términos generales: 1).- Que el espacio escenario de los fenómenos físicos, es un espacio euclídeo tridimensional. Esto significa que se trata de un espacio tridimensional plano y uniforme en el que a cada posición determinada por una terna de coordenadas le corresponde un solo punto físico. 2).- Que electrones y positrones son partículas puntuales cargadas. 3).-Que la interacción electromagnética y la gravitación son dos fenómenos que no tienen nada que ver entre sí.
En nuestra teoría geométrica de los entes fundamentales se revisan estas suposiciones y se especula con: 1).-Que la estructura del espacio de la realidad física pudiera ser ser la de un "espacio multiple" en el que a cada posición le correspondería mas de un "punto físico". Este espacio estaría inspirado en las secciones espaciales de un espacio-tiempo completo de Kerr. 2).- Que electrones y positrones desnudos son miniagujeros negros de Kerr. 3).-Que el electromagnetismo es una consecuencia del intercambio, por efecto de la gravitación, de partículas realmente elementales que orbitan a los miniagujeros negros de Kerr que constituyen las partículas.
La métrica de Kerr, inspiradora de nuestro modelo de espacio físico, corresponde a una familia de soluciones exactas de las ecuaciones de Einstein para campo vacío que describe agujeros negros con masa y con momento angular. En la sección 2 de este artículo se describen las peculiaridades de esta solución dada a conocer en 1963, es decir mucho tiempo después del desarrollo de la mecánica cuántica.
La métrica de Kerr descubre un complicado espacio-tiempo que no puede ser cubierto con un solo sistema de coordenadas como los usados habitualmente para cubrir todo el espacio-tiempo plano. Dado que se necesitan múltiples sistemas de coordenadas para cubrir el espaciotiempo completo de Kerr se dice que este consta de multiples universos. En la sección 3 de este artículo se describen algunas versiones del espaciotiempo completo de Kerr y se apunta su posible relación con la estructura del espacio físico y con un modelo de electrones y positrones desnudos.
En nuestro modelo de las partículas cargadas estas se presentan como miniagujeros negros de Kerr orbitados por cierto tipo de partículas (a las que hemos denominado prefotones, PF, ver artículo 1, adjunto) de velocidad v=c. A este fin se describen en la seccion 4 las posibles trayectorias de partículas de masa nula alrededor de los agujeros negros de Kerr.
Finalmente se presentan en la sección 5 de este artículo las hipótesis que soportan los modelos geométricos de electrones y positrones geométricos así como el mecanismo gravitacional de las interacciones electromagnéticas.
En 1963, R.P. Kerr presentó una solución exacta a las ecuaciones de Einstein dependiente de dos parámetros, m y a, que se pueden interpretar como la masa y el momento angular específico (a=S/m; S=spin) de un agujero negro.
R.H. Boyer y R.W. Lindquist, [1] estudiaron el espacio-tiempo completo descrito por la métrica de Kerr. Asimismo expresaron esta métrica en unas coordenadas adecuadas a una interpretación intuitiva del campo gravitatorio. Estas coordenadas de Boyer y Lindquist, (BL), son unas coordenadas esferoidales adaptadas al espacio curvo y su relación con las coordenadas cartesianas se deduce de las siguientes ecuaciones:
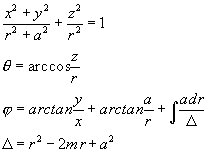 (1)
(1)
Es fácilmente constatable que las superficies r=cte son elipsoides de revolución y que para a=0 estas coordenadas se reducen a las coordenadas esféricas.
La expresión de la métrica de Kerr en coordenadas BL es la siguiente:
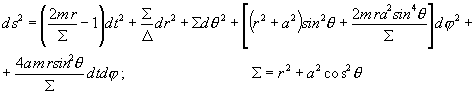 (2)
(2)
A la vista de este elemento de línea se puede deducir que se describe un campo gravitatorio estacionario y axialsimétrico ya que las ga b no dependen ni de t ni de j . Al mismo tiempo se aprecia y que el espacio-tiempo correspondiente es asintóticamente plano ya que para r® ¥ la métrica se aproxima a la del espacio-tiempo plano en coordenadas esféricas.
Se puede constatar que las singularidades de la métrica de Kerr (los puntos donde algún ga b alcanza valores infinitos) están definidos por: S =0; y D =0;
La ecuación: S =0 con solución: r=0; q =p /2; implica que z/r=0; y que la línea x2+y2=a2, es un anillo singular que puede ser considerada como el centro del agujero negro. Se trata de una singularidad esencial, es decir física, que no se puede evitar con ningún cambio de coordenadas y donde la curvatura del espacio-tiempo alcanza valores infinitos. En este anillo singular es donde se concentra toda la masa-energía del agujero negro. Al contrario de lo que ocurre con la singularidad puntual de la métrica de Swarzschild, la singularidad anular de la métrica de Kerr es evitable ya que por una parte en las proximidades del anillo la gravedad resulta ser repulsiva. Por otra parte cualquier partícula que se acerque al centro del agujero negro siguiendo trayectorias de ángulos distintos a q =p / 2 atravesará el anillo singular pasando a un espacio caracterizado por valores de r negativos. En estas regiones o universos negativos una partícula se comportaría como si estuviera en el exterior de un campo gravitatorio creado por una masa de valor negativo. Esto puede entenderse teniendo en cuenta que la métrica (2) es invariante por las sustituciones: r® -r; m® -m.
También resulta invariante la métrica por las sustituciones: a® -a; j ® -j .
Teniendo en cuenta las anteriores invarianzas y aceptando la posible existencia de masas y universos negativos, podrían considerarse cuatro situaciones inequivalentes definidas por la misma métrica de acuerdo a los signos de: {a,m,r}. Estas situaciones serían las correspondientes a los siguientes conjuntos de signos: 1.{+,+,+} 2.{+,-,-} 3.{-,+,+} 4.{-,-,-}.
Aparte de la singularidad esencial de tipo anular ya comentada, la métrica (2) presenta otras singularidades imputables al sistema de coordenadas BL. Se trata de los puntos definidos por los valores de r correspondientes a las raíces de la ecuación: D =0:
![]() (3)
(3)
Las soluciones: r=r+ y r=r- , corresponden a dos superficies cerradas singulares que pueden ser evitadas con convenientes cambios de coordenadas. Estas superficies "pseudosingulares" son típicas de los agujeros negros y se las conoce con el nombre de horizontes del espacio-tiempo.
Cabe considerar 3 casos especiales:
1.-Cuando a=0 la métrica (2) se reduce a la métrica de Swarzschild, la singularidad se reduce a un punto, y existe un solo horizonte situado en r=2m.
2.-Cuando a=m los dos horizontes se confunden en uno solo situado en r=m.
3.-Cuando a>m no existen soluciones de la ecuación D =0 y la singularidad no esta separada del universo exterior por ningún horizonte. En este caso se habla de una singularidad desnuda.
Las pseudosingularidades revelan que con un sistema de BL no se pueden etiquetar todos los sucesos de un espaciotiempo completo de Kerr. Las distintas posibilidades de espaciotiempo de Kerr completo interesantes para la construcción de nuestro modelo, son el objeto de la próxima sección.
3 Versiones del espacio-tiempo completo de Kerr.
El estudio de las geodésicas de la métrica de Kerr revela que la distancia y el tiempo propios (con origen en un suceso arbitrario) de una partícula que cruza el horizonte r+, tienen valores finitos en dicho horizonte. Sin embargo en el momento de cruzar las coordenadas t y
j de BL siempre tienen valores infinitos. Si suponemos que nuestro universo es el conjunto de sucesos abarcados por un sistema de coordenadas BL { t,r,q ,j }, se puede considerar que la partícula al cruzar el horizonte sale de nuestro universo ya que no hay valores de t Î { t,r,q ,j }, para sus sucesos. Esta partícula entraría en una región no cubierta por el sistema BL y que por consiguiente no pertenece a nuestro universo pero que sí pertenece a la realidad física.De lo anterior se deduce que con un solo sistema de coordenadas BL no se puede cubrir todo el espacio-tiempo donde la métrica de Kerr es válida y por donde sus geodésicas pueden ser prolongadas. Sin ir mas lejos para los sucesos interiores al horizonte r=r+ (que pueden ser alcanzados en valores finitos del tiempo propio) no hay valor de la coordenada t de BL. Resulta pues que este horizonte es como una frontera donde empieza y acaba la coordenada temporal de BL, es decir donde empieza y acaba nuestro tiempo absoluto newtoniano. Para poder etiquetar todos los sucesos de las líneas de universo que entran y salen de un agujero negro de Kerr es preciso por lo tanto usar nuevos sistemas de coordenadas que nos vayan descubriendo las diversas regiones del espacio-tiempo completo de Kerr. Recordemos que para que un espacio-tiempo sea completo es necesario que cualquier geodésica: {x
a =xa (t )}, (salvo las que acaban en una singularidad esencial) pueda ser prolongada hasta valores infinitos de su tiempo propio, t .Deducir todas las regiones que existen en el espacio-tiempo completo de Kerr y obtener los sistemas de coordenadas con que cubrir estas regiones es el objetivo de la prolongación analítica de la métrica de Kerr. En las referencias [1][2][3] pueden encontrarse de forma detallada los resultados y procedimientos de esta prolongación analítica, por lo tanto aquí solo exponemos un resumen de los resultados mas relevantes.
Generalmente en la prolongación analítica de la métrica de Kerr se utilizan dos sistemas de coordenadas: {Ei}, {Eo}. Estos sistemas permiten etiquetar los sucesos interiores al horizonte exterior: r=r+ y ampliar así la región: {0}
º (que identificamos con nuestro universo), con otras regiones interiores como la {1}º {r-<r<r+} y con otras regiones como la {2}º {-¥ <r<r-} que pueden considerarse universos exteriores pero con valores de r negativos. En el caso de que a=m no existe la región {1} ya que en este caso r+=r-=m; (ver figura 1 y figura 2).El sistema {Ei}
º {ti,r,q ,j i} permite etiquetar sucesos de las regiones {1} y {2} correspondientes a geodésicas que salen de nuestro universo y entran en una región interior futura del agujero negro. Del mismo modo el sistema: {Eo}º {to,r,q ,j o} permite etiquetar sucesos de otras regiones interiores pasadas: {-1} {-2} correspondientes a geodésicas que salen hacia el exterior.Lo mas notable de estos dos sistemas de coordenadas es que permiten prolongar las geodésicas por regiones de valores negativos de r. Efectivamente, las partículas que se acercan al anillo r=0, en un plano distinto al:
q =p /2, pueden atravesar este anillo singular sin chocar o rebotar con él y acceder de este modo a universos negativos: {-¥ <t<¥ , -¥ <r<r- , 0<q <p , 0<j <2p }. En definitiva cada sistema de coordenadas E cubre tres regiones: Un universo exterior positivo: {r+<r<¥ }, una región interior: {r-<r<r+}, (inexistente en el caso a=m) y una región: {-¥ <r<r-} que se extiende a un universo exterior negativo.Del mismo modo como se prolonga la región {0} se pueden prolongar las regiones: {1} {2} {-1} {-2} obteniéndose nuevas regiones de los mismos tipos que a su vez pueden ser prolongadas. El resultado final consiste en una sucesión infinita de regiones como las descritas en el párrafo anterior. Estas regiones se suelen representar mediante diagramas de Penrose donde se realiza una especie de compresión conforme del espaciotiempo para representar las regiones alejadas infinitamente. Estos diagramas espaciotiempo conservan la propiedad de representar las líneas de universo de fotones inclinadas a 45 o 135 grados. Las líneas correspondientes a los horizontes, las hemos representado en gris y dada su inclinación se puede comprobar que los horizontes son superficies generadas por dos familias de trayectorias de fotones que suelen denominarse "congruencias nulas principales".
En la figura 1 se representa los diagramas correspondientes al caso: 0<a<m.
 A la vista de la figura [1.a] se puede apreciar que esta consiste en una repetición indefinida, hacia arriba y hacia abajo, del bloque formado por: los 4 cuadrados: {0}, {1*=1}, {0*}, {-1*=-1}, y los cuatro cuadrados: {2*}, {3*=3}, {2}, {1*=1}, que están solapados a los anteriores por la región: {1*=1}.
A la vista de la figura [1.a] se puede apreciar que esta consiste en una repetición indefinida, hacia arriba y hacia abajo, del bloque formado por: los 4 cuadrados: {0}, {1*=1}, {0*}, {-1*=-1}, y los cuatro cuadrados: {2*}, {3*=3}, {2}, {1*=1}, que están solapados a los anteriores por la región: {1*=1}.
El cuadrado {0} representa a una región exterior positiva, {r+<r<¥ }, que asumimos corresponde a nuestro universo.
El cuadrado {0*} representa a otra región exterior positiva que junto con nuestro universo forma un puente Einstein-Rosen similar al de la métrica de Schwarzschild.
El cuadrado {-1*= - 1} representa una región interior, {r-<r<r+}, que es común en el sistema de coordenadas: Eo º {0}È {-1}È {-2} y el sistema de coordenadas Eiº {0*}È {-1*}È {-2*}.
El cuadrado {1*=1} representa una región interior, {r-<r<r+}, que es común en el sistema de coordenadas: Ei º {0}È {1}È {2} y el sistema de coordenadas Eoº {0*}È {1*}È {2*}.
La razón para representar contiguas las anteriores cuatro regiones es la existencia de un nuevo sistema de coordenadas mas amplio (K) que las cubre completamente: El sistema de coordenadas Kº {v,u,q ,w} donde la coordenada v es temporal en todo su rango (que va desde -¥ hasta ¥ ) , la coordenada u es espacial y con el mismo rango, y la coordenada w tiene un rango que va desde 0 hasta 2p . La región {0} se identifica con el cuadrante este: {u>| v| } del plano {u,v}, y las regiones {1}, {0*}, y {-1} con los cuadrantes norte oeste y sur del mismo plano {u,v}, respectivamente.
Algo semejante ocurre con los cuatro cuadrados: {2*}, {3}, {2}, {1}, que pueden ser cubiertos totalmente por otro sistema de coordenadas K'º {v',u',q ',w'}.
A partir de las relaciones directas entre los sistemas: K y K': se puede comprobar la correspondencia biunívoca entre el cuadrante norte de uno de estos sistemas con el cuadrante sur del otro, lo que indica la posibilidad de establecer una correspondencia biunívoca entre los sucesos de las regiones {-1*= - 1} y {3*=3} . Lo anterior permitiría hacer una identificación de estas dos regiones y obtener así la versión mas simple (versión minimal) de un espaciotiempo completo de Kerr en el caso 0<a<m: Este espaciotiempo completo minimal estaría compuesto por 6 regiones esencialmente distintas: dos universos exteriores positivos, {0}, {0*}, dos universos exteriores negativos, {2*}, {2}, y dos regiones interiores, {1*=1}, {-1*= - 1=3*=3}. Figura 1.b.
Nada impide especular con que en la realidad física, un cierto número de universos exteriores tales como los descritos se encuentran superpuestos de forma que cada punto de el espacio fuera una superposición de cierto número de puntos correspondientes cada uno de ellos a un universo distinto. En el caso de el espaciotiempo completo minimal de Kerr (0<a<m) habría cuatro de estos puntos: dos de ellos pertenecientes a sendas hojas positivas del espacio y dos de ellos pertenecientes a hojas negativas. Las cuatro hojas del espacio estarían desconectadas entre si salvo en el centro del agujero negro a través de las regiones interiores.
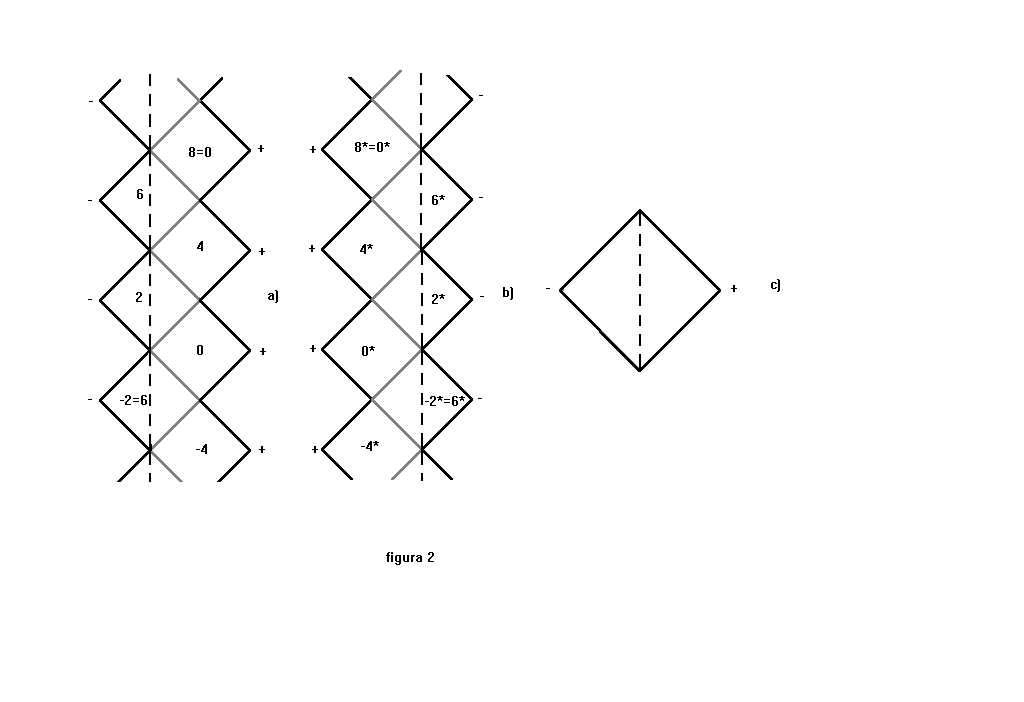 En las figuras 2a y 2b se representan los diagramas espaciotiempo de agujeros de Kerr con a= ± m. Dichas figuras deben suponerse prolongadas indefinidamente hacia arriba y hacia abajo. Versiones de espaciotiempos completos serían las constituidas por estas sucesiones de infinitos universos positivos y negativos resultantes de la prolongación analítica sucesiva de los universos iniciales. También serían espaciotiempos completos los resultantes de la identificación de algún universo con otro universo posterior o anterior. En la figura hemos supuesto estas identificaciones para formar 2 versiones de espaciotiempo completo con cuatro universos:1.- {{0=8}, {2}, {4}, {6}} y 2.- {{0*=8*}, {2*}, {4*}, 6*}}. Cada una de estas versiones correspondería a dos espaciotiempos de valores opuestos del momento angular del agujero negro. Consideramos que cada uno de las dos versiones de espaciotiempo completo, podrían ser adecuadas para modelos de electrones spin up y electrones spin down respectivamente.
En las figuras 2a y 2b se representan los diagramas espaciotiempo de agujeros de Kerr con a= ± m. Dichas figuras deben suponerse prolongadas indefinidamente hacia arriba y hacia abajo. Versiones de espaciotiempos completos serían las constituidas por estas sucesiones de infinitos universos positivos y negativos resultantes de la prolongación analítica sucesiva de los universos iniciales. También serían espaciotiempos completos los resultantes de la identificación de algún universo con otro universo posterior o anterior. En la figura hemos supuesto estas identificaciones para formar 2 versiones de espaciotiempo completo con cuatro universos:1.- {{0=8}, {2}, {4}, {6}} y 2.- {{0*=8*}, {2*}, {4*}, 6*}}. Cada una de estas versiones correspondería a dos espaciotiempos de valores opuestos del momento angular del agujero negro. Consideramos que cada uno de las dos versiones de espaciotiempo completo, podrían ser adecuadas para modelos de electrones spin up y electrones spin down respectivamente.
Finalmente nos queda el caso de un agujero negro de Kerr con a>m correspondiente a lo que se denomina con el nombre de "singularidad desnuda". En este caso no existen horizontes y el espaciotiempo completo consta solo de dos universos, uno positivo y otro negativo, separados por una singularidad anular. El diagrama espaciotiempo es el representado en la figura 2c.
Hasta aquí la descripción de algunas versiones de espaciotiempo completo de Kerr. Todas tienen en común la existencia de universos exteriores positivos y negativos. Lo que sugieren en conjunto todas ellas es que el espacio de la física pudiera ser múltiple. Es decir que en un punto del espacio en realidad se superpondrían una multiplicidad de puntos pertenecientes a diversos universos positivos o negativos. Por otra parte la existencia de singularidades y horizontes inocuos (es decir no destructivos), sugiere que la parte central del agujero negro sería una zona de interconexión entre los distintos espacios. Lo que se pretende es construir un modelo donde las partículas fueran miniagujeros negros de Kerr que conectarían en sus posiciones estos espacios superpuestos e inconexos lejos de la materia.
La realidad de las versiones de espaciotiempo obtenidas por identificación diversos universos ha sido rechazada en el ámbito de la astrofísica por motivos relacionados con el principio de causalidad: Efectivamente en estos espaciotiempos pueden darse trayectorios temporales cerrradas que supondrían una violación del citado principio, Carter (1968). No obstante no hay ninguna prueba, sino mas bien al contrario, de que el principio de causalidad en su forma mas restrictiva deba ser tenido en cuenta en el ámbito de la física de las partículas elementales.
La cuestión que resta es decidir cual de la versiones disponibles es en principio mas adecuada para la construcción de un modelo geométrico de las partículas. Este tema lo dejamos para la sección 5.
El campo gravitatorio de un agujero negro de Kerr, encierra muchas sorpresas. A las ya señaladas en secciones anteriores hay que añadir el carácter repulsivo de las singularidades a corta distancia mientras que a distancias mayores son atractivas. Otra característica interesante es el hecho de que en el campo gravitatorio alrededor las singularidades existen infinidad de posibles órbitas cerradas de partículas nulas (partículas cuya velocidad es c). Todo esto se ha podido poner de manifiesto mediante el estudio de las geodésicas de la métrica.
Las órbitas y trayectorias de fotones y neutrinos en el espacio-tiempo de Kerr se han investigado sistemáticamente por muchos autores con ayuda de las ecuaciones de las geodésicas deducidas por B. Carter (1968), [3]. Aquí se describirán cualitativamente las características del movimiento de partículas nulas, (PN), que se acercan a una singularidad de Kerr desde un universo exterior.
De las referidas ecuaciones de Carter se deduce que el movimiento de las PN sigue líneas de valor constante de la coordenada
q . (q =0 para partículas que se acerquen paralelamente al eje de rotación, q = p / 2 para partículas que se acerquen en el plano ecuatorial, y valores intermedios para otras trayectorias). Además las distintas trayectorias dependen de un parámetro de impacto L, que como es habitual indica si la trayectoria está dirigida mas o menos hacia el centro del agujero negro.Para cada valor de
q existen dos valores de L que corresponden a dos trayectorias en las que el valor de la coordenada radial permanece constante. A las trayectorias de r constante las llamaremos, aunque algo impropiamente, órbitas circulares. Una de las citadas órbitas circulares corresponde a PN que giran en el mismo sentido de giro que el agujero negro. La otra órbita es exterior a la anterior (con mayor valor de r) corresponde a PN girando en sentido contrario. Estas órbitas son inestables, lo que quiere decir que una pequeña perturbación puede provocar que la PN inicie un movimiento espiral hacia dentro o hacia fuera del agujero negro. El conjunto de todas estas órbitas formarían lo que podríamos llamar dos esferas fotónicas, siendo una de estas esferas interior a la otra.Para valores de L mayores al correspondiente a la órbita exterior la PN escapará al universo interior, pero para parámetros de impacto menores al correspondiente a la órbita interior pueden ocurrir varias cosas:
Si el parámetro de impacto es cero o valores muy próximos a cero la PN atravesará la singularidad anular y entrara en el espacio negativo, donde alcanzará valores de r negativos y sentirá una gravedad negativa, es decir repulsiva, que la hará alejarse de la singularidad.
Cuando el parámetro de impacto es el adecuado para que la partícula se aproxime a la singularidad por la parte exterior del anillo hay un balance entre la atracción y la repulsión y como resultado las PN pueden adquirir órbitas circulares que son mas estables que las consideradas hasta ahora. Estas órbitas estables son interesantes porque pueden hacer de las proximidades del anillo singular una especie de almacén de partículas nulas.
Hay aun otras posibles órbitas circulares pero esta vez en el espacio negativo. Son las que adquieren partículas con un cierto rango de parámetros de impacto correspondientes a trayectorias cercanas al anillo pero por la parte interior de este. Estas órbitas se llaman pendulares ya que la trayectoria de la partícula transcurre en una superficie elipsoidal en el espacio negativo rebotando entre distintos puntos de la singularidad.
Respecto a las partículas que se acerquen al agujero negro desde el espacio negativo, solo las que lo hagan en trayectorias axiales o próximas al eje de rotación, conseguirán pasar al universo positivo. Para las demás partículas la singularidad es repulsiva y les hará rebotar de nuevo hacia el infinito espacial del universo negativo de procedencia. Suele decirse que visto desde un universo negativo, el agujero negro de Kerr es una fuente de antigravedad.
Hasta aquí un resumen cualitativo de las posibles trayectorias de partículas nulas en las proximidades de una singularidad de Kerr donde se supone que las partículas no perturban apreciablemente al campo gravitatorio.
Para poder imaginar lo que ocurriría en un "mini espaciotiempo completo de Kerr" como el de nuestro modelo habría que considerar la multiplicidad de universos y singularidades que comprende y estudiar las posibles líneas de universo cerradas. También habría que considerar y estudiar el caso en el que las propias partículas orbitantes provoquen una perturbación apreciable de la métrica.
Para dar verosimilitud a un modelo geométrico de electrones y positrones, así como para especular con un mecanismo gravitacional del electromagnetismo, es necesario introducir algunas ideas o hipótesis adicionales:
El hecho de la existencia de electrones y positrones con valor cuantificado de sus masas y espines nos sugiere basar sus modelos geométricos en espaciotiempos completos de Kerr cuyas parámetros cumplan: a2=m2 . Esta ecuación da lugar a cuatro soluciones con combinaciones de signos de m y de a: {+,+}, {+,-}, {-,+}, {-,-}, que se harían corresponder con los cuatro estados: electrón up, electrón dawn, positrón up, positrón dawn.
La elección de estos valores que cumplen:
| a| =| m| se apoya por una parte en el hecho de la cuantificación del spin y la masa de electrones y positrones. Por otra parte en que a=m. es un valor especial al que tienden los agujeros negros de Kerr de dimensiones astrofísicas. Conviene aclarar que no interpretamos que m deba coincidir con la masa del electrón físico (vestido) ni a como su spin específico. Estos valores en unidades geometrizadas son: me=6.76× 10-56cm y ae=s/me=(1.306× 10-66cm2)/(me)=0.193× 10-10cm. Como podemos ver ae>>me . Los valores ± m de la masa y ± a del momento angular específico de electrones y positrones desnudos evidentemente deben ser distintos a los correpondientes a las partículas físicas.Los valores negativos del momento angular no presentan ningún problema de interpretación ni de asignación de los espaciotiempos correspondientes. Los modelos de electrones correponderían a los signos: {m=+,a=+} y {m=+,a
= - }. Los diagramas espaciotiempo correspondientes serían los representados en las figuras 3a y 3b, que son iguales a los de las versiones descritas en la sección 3 y representados en las figuras 2a, y 2b. Pero para los positrones cuyos signos serían: {m= - ,a=+} y {m= - ,a= - } las masas son negativas y por lo tanto es necesario aclarar el significado de un espaciotiempo de masa negativa. La pista nos la da la invarianza de la métrica dos (2) bajo las transformaciones: r® -r; m® -m. En un espaciotiempo completo de Kerr de masa negativa habría como en el caso de la masa positiva, hojas de espacio positivas y negativas. Las regiones negativas de un espaciotiempo de masa negativa serían semejantes a las regiones positivas de un espacio-tiempo de masa positiva, por lo tanto el horizonte se situaría en el valor: r= - | m| . Las regiones positivas de un espaciotiempo de masa negativa serían semejantes a las regiones negativas de un espaciotiempo de masa positiva, por tanto serían como el exterior de un campo gravitatorio creado por una masa positiva.
Pero para los positrones cuyos signos serían: {m= - ,a=+} y {m= - ,a= - } las masas son negativas y por lo tanto es necesario aclarar el significado de un espaciotiempo de masa negativa. La pista nos la da la invarianza de la métrica dos (2) bajo las transformaciones: r® -r; m® -m. En un espaciotiempo completo de Kerr de masa negativa habría como en el caso de la masa positiva, hojas de espacio positivas y negativas. Las regiones negativas de un espaciotiempo de masa negativa serían semejantes a las regiones positivas de un espacio-tiempo de masa positiva, por lo tanto el horizonte se situaría en el valor: r= - | m| . Las regiones positivas de un espaciotiempo de masa negativa serían semejantes a las regiones negativas de un espaciotiempo de masa positiva, por tanto serían como el exterior de un campo gravitatorio creado por una masa positiva.
El campo exterior de una masa negativa sería múltiple, al igual que el creado por una masas positiva. Las curvaturas de las distintas hojas del espacio en el exterior de un agujero de masa -m serían iguales a las de un agujero negro de masa m. Esto haría que ambos campos fueran indistinguibles a cierta distancia de los horizontes. No obstante la absorción o emisión de partículas realmente elementales, causarían reacciones opuestas en una masa negativa a las causadas en una masa positiva. Recordamos que las partículas "realmente elementales" de nuestro modelo geométrico, los PF, son supuestas perturbaciones que afectan a una solo hoja del espacio.
Los diagramas espaciotiempo relativos a estas masas negativas se presentan en las figuras 3c y 3d. Cada una de ellas corresponde, como en el caso de las figuras 3a y 3b, a cada uno de los dos signos posibles del momento angular.
Se establece con la introducción de campos gravitatorios de masa negativa una simetría conveniente a nuestro modelo que no solo no es contraria a la teoría de Einstein sino que creemos que es atractiva por razones "estéticas y filosóficas".
Para completar la simetría de la teoría de la gravitación deben considerarse también la posibilidad de partículas de prueba de masas positivas y negativas. La conveniencia de este concepto se pondrá de manifiesto en nuestra explicación de las interacciones electromagnéticas basadas en la gravitación. Las partículas elementales de nuestro modelo geométrico, (prefotones , PF) podran ser por tanto de masa (infinitésimal) positiva o negativa. La peculiaridad esencial de las partículas de masa negativa es la de que en su movimiento el vector velocidad y el vector impulso tienen valores opuestos. Esta propiedad caracterizaría a estas partículas de masa negativa cuyo comportamiento en choques con otras partículas sería el opuesto al que cabría esperar en los choques de partículas de masa positiva.
Con la citada simetrización de fuentes y partículas gravitatorias se pueden construir modelos de las atraciones y repulsiones electromagnéticas basados en el intercambio de PF Este intercambio será entre agujeros negros de Kerr de signos iguales para el caso de repulsiones y de distinto signo en caso de atracciones. El mecanismo sería el siguiente:
La proximidad de dos miniagujeros negros orbitados por PF corresponde en el modelo geométrico a la proximidad de dos partículas cargadas. La perturbación mutua del espaciotiempo debida a esta proximidad provocaría que ambos agujeros negros emitan y absorban PF de los residentes en sus respectivas órbitas estables que rodean a sus anillos singulares. Concretamente en el mecanismo que expondremos mas adelante, (que no es el unico imaginable), un agujero de signo + (electrón) emitiría doble número de PF positivos que de PF negativos. De forma simétrica un agujero de signo - (positrón) emitiría doble número de objetos corpusculares negativos que de objetos corpusculares positivos.
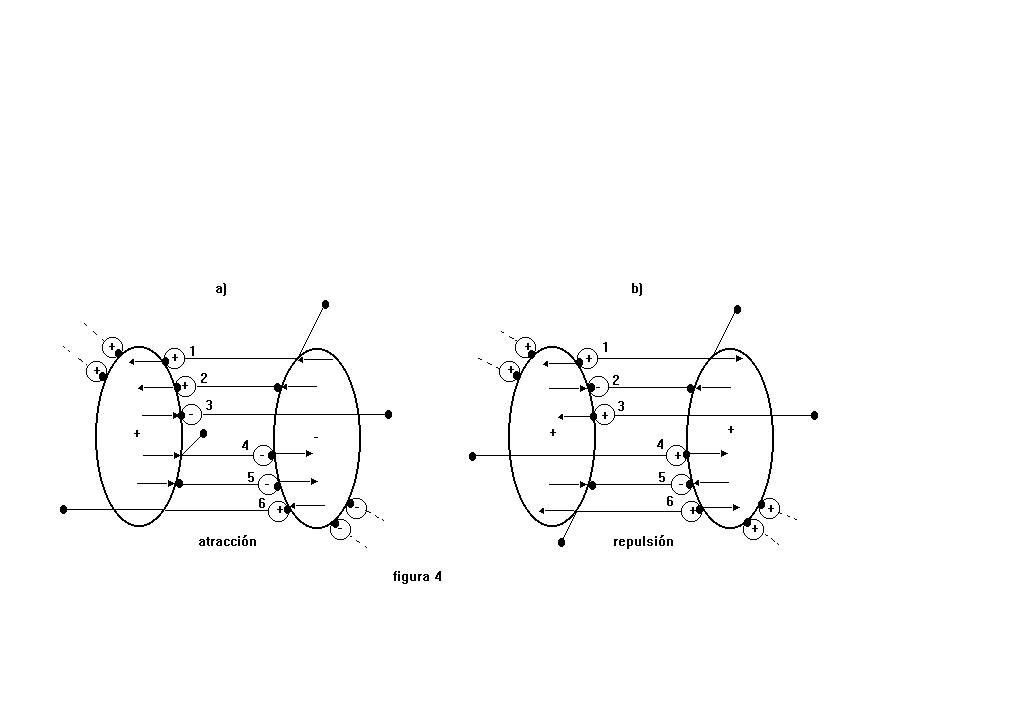
La figura 4a esquematiza la atracción entre un positrón y un electrón.
La elipse de la parte izquierda, con un signo + en el centro, corresponde al electrón. La elipse de la parte derecha, con un signo - en el centro corresponde al positrón. Concretamente se pretende esquematizar con estas elipses a las órbitas estables que discurren en las proximidades del anillo singular de un espaciotiempo de masa positiva y de un espaciotiempo de masa negativa. Cada una de estas partículas emite tres PF que en la figura están representados con círculos numerados que rodean al signo correspondiente. La reacción de las partículas cargadas a la emisión o absorción de los PF está representada por unas flechitas que indican el movimiento de reacción. Se puede apreciar que esta reacción es opuesta a la habitual cuando los signos de las partículas cargadas y PF son distintos.
El PF numero 1 es un positivo que emite el electrón y que es dispersado elásticamente por el positrón. El efecto que produce sobre las partículas cargadas es un desplazamiento de ambas hacia la izquierda que representamos por las dos flechitas que apuntan en esa dirección.
El PF 2 también es positivo y es emitido por el electrón y absorbido por el positrón. El efecto es un par de desplazamientos de ambas partículas hacia la izquierda iguales que los producidos por el PF 1.
El PF 3 es negativo, emitido por el electrón y atraviesa el anillo singular del positrón. Su efecto se deja sentir solo en el electrón y consiste en un desplazamiento hacia la derecha de este electrón.
El PF número 4 es negativo y es emitido por el positrón siendo dispersado por el electrón. Su efecto es el opuesto al del PF 1: Es decir el desplazamiento del electrón y el positrón hacia la derecha. Este efecto compensa al producido por el PF 1.
El PF 5 es un negativo, emitido por el positrón que va a parar al anillo singular del electrón. Su efecto es igual al producido por el PF 4, es decir un desplazamiento de ambas partículas hacia la derecha, es decir el efecto compensador opuesto al producido por el PF 2.
El PF 6 es un positivo emitido por el anillo singular del positrón que atraviesa el anillo singular del electrón. Su efecto es un desplazamiento de positrón hacia la izquierda.
En resumen: los efectos de los PF 1 y 2 se compensan con los del los 4 y 5. El efecto neto es el producido por los PF 3 y 6: un desplazamiento del electrón hacia la derecha y un desplazamiento del positrón hacia la izquierda. Es decir la atracción de estas dos partículas.
Para conseguir la conservación del número de PF en las órbitas de cada anillo, es preciso que dos PF de los residentes en las orbitas inestables (las esferas fotónicas) de cada partícula pasen a los respectivas órbitas anulares. Este traspaso lo representamos en la figura por los correspondientes circulos con sus signos. En los referidos traspasos no se producen desplazamientos neto de las partículas por tratarse de transferencias de impluso internas al sistema.
El mecanismo de repulsión electromagnética está representado en la figura 4b. En ella se esquematizan dos electrones. Como podrá suponerse el mecanismo de repulsión entre dos positrones sería semejante al de los electrones que pasamos a explicar:
El PF 1 es positivo, emitido por el electrón de la izquierda y dispersado por el de la derecha. El efecto consiste en unos desplazamiento de ambas partículas en sentidos opuestos es decir tendiendo a separarlas.
El PF 2 es negativo, emitido por el electrón de la izquierda y absorbido por el de la derecha. El efecto sería un acercamiento de ambas partículas que compensaría el alejamiento de debido al primer PF
El PF 3 es positivo, emitido por el electrón de la izquierda y atraviesa el anillo singular del otro electrón. Su efecto se dejaría sentir solo en el electrón de la izquierda y consiste en un desplazamiento hacia la izquierda este electrón.
El efecto neto de los PF 1, 2 y 3 sería este último desplazamiento hacia la izquierda. De forma simétrica el efecto neto de los PF 4, 5 y 6 sería un desplazamiento del electrón de la derecha hacia la derecha. El efecto total de estos dos desplazamientos sería una repulsión de los dos electrones.
Referencias:
[1] Boyer, R.H., Lindquist, R.W. (1967). J. Math. Phys., 8,265.
[2] Carter, B. (1966). Phys. Rev., 141,1242.
[3] Carter, B. (1968). Phys. Rev., 174,1559.