Método de Newton para raíces complejas.
Conjuntos de Julia y de Mandelbrot
Javier Pérez González
Departamento de Análisis Matemático
Universidad de Granada
Aproximación de raíces complejas por el método de Newton
Como seguramente ya sabes, el método de Newton es una técnica frecuentemente usada para calcular soluciones de una ecuación f(z)=0. Para ello, se elige un valor inicial 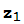 y, a partir de él, se forma la sucesión definida por
y, a partir de él, se forma la sucesión definida por 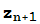 =
=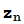 -
-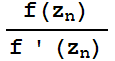 . Si dicha sucesión converge, su límite es una solución de la ecuación f(z)=0. Naturalmente, cuando hay más de una solución, la elección del valor inicial determina a cuál de ellas converge el proceso.
. Si dicha sucesión converge, su límite es una solución de la ecuación f(z)=0. Naturalmente, cuando hay más de una solución, la elección del valor inicial determina a cuál de ellas converge el proceso.
Mathematica tiene un comando "FindRoot[f(z)=0,{z,a}]" que utiliza precisamente el método de Newton para calcular soluciones de la ecuación f(z)=0 a partir del valor inicial z=a. Evalúa la siguiente celda.
In[1]:=
![FindRoot[z^2 + 1 == 0, {z, 0.5}]](HTMLFiles/index_5.gif)
Out[1]=
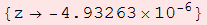
¿Sabes por qué ha fallado el método en este caso particular? Fíjate en cómo se van obteniendo las aproximaciones sucesivas 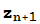 =
=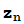 -
-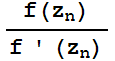 . Es evidente que, para f(z)=
. Es evidente que, para f(z)=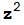 +1 partiendo de un valor real obtenemos siempre valores reales por lo que el método no puede proporcionarnos las raíces de
+1 partiendo de un valor real obtenemos siempre valores reales por lo que el método no puede proporcionarnos las raíces de 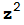 +1 =0 que son complejas. Repite con una ligera variante.
+1 =0 que son complejas. Repite con una ligera variante.
In[2]:=
![FindRoot[z^2 + 1 == 0, {z, 0.5 + 0.1}]](HTMLFiles/index_12.gif)
Out[2]=
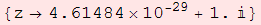
Ahora Mathematica ha calculado la solución z=i con gran precisión. Observa ahora el efecto de cambiar un poco el valor inicial.
In[3]:=
![FindRoot[z^2 + 1 == 0, {z, 0.5 - 0.1}]](HTMLFiles/index_14.gif)
Out[3]=
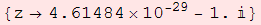
Si quieres, puedes ver las sucesivas aproximaciones y los correspondientes valores de la función.
In[4]:=
![z[0] = 0.5 + 0.1 ;](HTMLFiles/index_16.gif)
![z[n_] := z[n] = z[n - 1] - (z[n - 1]^2 + 1)/(2 z[n - 1]) ;](HTMLFiles/index_17.gif)
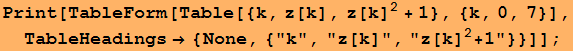
| k |
z[k] |
![2 z[k ] +1](HTMLFiles/index_19.gif) |
| 0 |
0.5+0.1 i |
1.24+0.1 i |
| 1 |
-0.711538+0.242308 i |
1.44757-0.344822 i |
| 2 |
0.273911+0.335585 i |
0.96241+0.183841 i |
| 3 |
-0.59291+1.062 i |
0.223705-1.25934 i |
| 4 |
-0.0960636+0.889932 i |
0.21725-0.17098 i |
| 5 |
0.0119175+1.00034 i |
-0.000529077+0.0238431 i |
| 6 |
4.84133*10^^-6+0.999929 i |
0.000141747+9.68198*10^^-6 i |
| 7 |
-3.43171*10^^-10+1. i |
-5.00034*10^^-9-6.86343*10^^-10 i |
Como puedes ver Mathematica aplica el método de Newton para calcular raíces tanto reales como complejas. Ahora bien, la intrepretación del método en el caso del cálculo de raíces reales no tiene sentido en el caso complejo. En el caso real, el punto 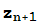 se obtiene como el punto de corte de la recta tangente a la curva y=f(z) en el punto (
se obtiene como el punto de corte de la recta tangente a la curva y=f(z) en el punto (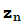 ,f(
,f(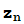 )) con el eje de abscisas y se conocen condiciones precisas que garantizan la convergencia del método. Lo que ocurre en el caso complejo puede ser mucho más complicado como vamos a ver.
)) con el eje de abscisas y se conocen condiciones precisas que garantizan la convergencia del método. Lo que ocurre en el caso complejo puede ser mucho más complicado como vamos a ver.
A continuación vamos a aplicar el método de Newton para calcular aproximaciones de las raíces del polinomio 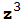 +1. Pidámosle a Mathematica que calcule dichas raíces.
+1. Pidámosle a Mathematica que calcule dichas raíces.
In[7]:=
![raices = z/.(Solve[z^3 + 1 == 0, z]/.(a_->b_) :> (a->ComplexExpand[b]))](HTMLFiles/index_24.gif)
Out[7]=
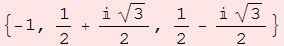
Sus aproximaciones numéricas son
In[8]:=
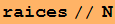
Out[8]=
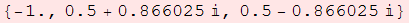
Observa que si f(z)=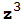 +1 entonces z-
+1 entonces z-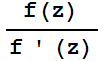 =
=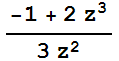 . La siguiente función "NewtonAprox" le dice a Mathematica que, partiendo de un valor inicial z=x+i y, calcule las sucesivas iteraciones del método de Newton para aproximar una solución de
. La siguiente función "NewtonAprox" le dice a Mathematica que, partiendo de un valor inicial z=x+i y, calcule las sucesivas iteraciones del método de Newton para aproximar una solución de 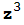 +1=0 y que se pare si en algún paso el valor obtenido de z verifica que |
+1=0 y que se pare si en algún paso el valor obtenido de z verifica que |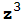 +1|≤0.001 o si ha llegado a la iteración número cincuenta. También le pedimos que imprima el último valor obtenido de z . La función está escrita haciendo uso de la opción "Compile" para que se ejecute más rápidamente.
+1|≤0.001 o si ha llegado a la iteración número cincuenta. También le pedimos que imprima el último valor obtenido de z . La función está escrita haciendo uso de la opción "Compile" para que se ejecute más rápidamente.
In[9]:=
![NewtonAprox = Compile[{{z, _Complex}}, Module[{w, k = 0}, w = z ; While[Abs[w^3 + 1] >0.001 && k≤50 && w≠0, w = (-1 + 2w^3)/(3 w^2) ; k = k + 1] ; w]] ;](HTMLFiles/index_33.gif)
Comprueba lo rápido que trabaja esta función evaluando la siguiente celda.
In[10]:=
![Table[NewtonAprox[x + y I], {y, -2, 2, .6}, {x, -2, 2, 1.25}]//MatrixForm](HTMLFiles/index_34.gif)
Out[10]//MatrixForm=

Observa cómo se obtiene una u otra raíz dependiendo del punto de partida. Lo que vamos a hacer ahora es asignarle a cada punto z=x+i y un valor distinto según cuál sea la raíz a la que converja el algoritmo anterior cuando se toma como valor inicial dicho punto. Concretamente, si la raíz a la que converge el método es -1 le damos a z el valor 0.15, si es 0.5 + 0.866 i le damos el valor 0.5 y si es 0.5 - 0.866 i le damos el valor 0.9. La razón de estos valores es que vamos a usarlos después para aplicarles la función de color "Hue". El color Hue[0.15] es amarillo, el Hue[0.5] es azul y el Hue[0.9] es rojo. Necesitamos redefinir la función "NewtonAprox". Procura entender lo que sigue.
In[11]:=

Ahora la función "NewtonColorAprox" ya no proporciona el útlimo valor de z calculado sino el valor asignado a z según el criterio anterior. Como "NewtonColorAprox" da siempre como resultado un número complejo a+b i , e incluso si b=0 escribe a+0i, nos quedamos con la parte real.
In[12]:=
![Table[Re[NewtonColorAprox[x + y I]], {y, -2, 2, .6}, {x, -2, 2, 1.25}]//MatrixForm](HTMLFiles/index_37.gif)
Out[12]//MatrixForm=
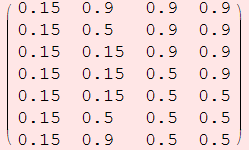
Lo que vamos a hacer ahora puede describirse más o menos como sigue. Dividiremos cada lado del cuadrado [-2,2]×[-2,2] en 500 partes, obtendremos así 500×500=250.000 cuadraditos. En cada uno de ellos tomamos un punto (x,y) y evaluamos en dicho punto nuestra función "NewtonColorAprox". Obtenemos así una matriz de 500 filas y 500 columnas a la que aplicamos la función de color "Hue". De esta forma, los puntos que convergen a la raíz -1 se colorean de amarillo, los que convergen a la raíz 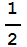 +
+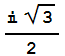 se colorean de azul y los que convergen a la raíz
se colorean de azul y los que convergen a la raíz 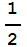 -
-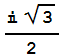 se colorean de rojo. Ten paciencia porque todo el proceso tarda unos 4 minutos pero merece la pena esperar.
se colorean de rojo. Ten paciencia porque todo el proceso tarda unos 4 minutos pero merece la pena esperar.
In[13]:=
![DensityPlot[NewtonColorAprox[x + y I], {x, -2, 2.}, {y, -2, 2}, PlotPoints→500, Mesh→False, AspectRatio→1, ColorFunction→Hue] ;](HTMLFiles/index_43.gif)
![[Graphics:HTMLFiles/index_44.gif]](HTMLFiles/index_44.gif)
Veamos ampliada la hoja superior del trébol central.
In[14]:=
![DensityPlot[NewtonColorAprox[x + y I], {x, -.6, 0.01}, {y, 0.01, .8}, PlotPoints→200, Mesh→False, AspectRatio→1, ColorFunction→Hue] ;](HTMLFiles/index_45.gif)
![[Graphics:HTMLFiles/index_46.gif]](HTMLFiles/index_46.gif)
Hagamos ahora una ampliación de la hoja superior del trébol que hay a la derecha.
In[15]:=
![DensityPlot[NewtonColorAprox[x + y I], {x, -.154, -0.088}, {y, 0.55, .7}, PlotPoints→200, Mesh→False, AspectRatio→1, ColorFunction→Hue] ;](HTMLFiles/index_47.gif)
![[Graphics:HTMLFiles/index_48.gif]](HTMLFiles/index_48.gif)
Así podríamos seguir indefinidamente. Observa que, aunque estos puntos están muy próximos convergen a distintas raíces. No parece cosa fácil entender este comportamiento. La frontera del conjunto que estamos representando tiene una estructura fractal. También es una buena imagen de lo que se llama caos matemático porque muestra que pequeñísimos cambios en los valores iniciales conducen a soluciones completamente diferentes.
Los conjuntos de Julia y de Mandelbrot
Los fractales más conocidos son los conjuntos de Julia y de Mandelbrot. Es muy fácil generar dichos conjuntos usando números complejos. Para cada número complejo c definamos la función 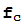 :C→C por
:C→C por 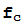 (z)=
(z)=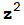 +c para todo z ∈ C. El conjunto de Julia asociado al número complejo c se define como el conjunto J(c) de los números complejos z tales que la sucesión definida por
+c para todo z ∈ C. El conjunto de Julia asociado al número complejo c se define como el conjunto J(c) de los números complejos z tales que la sucesión definida por 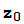 =z,
=z, 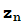 =
=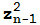 +c=
+c=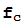 (
(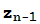 ) está acotada (algunos autores llaman conjunto de Julia a la frontera de J(c)). El conjunto de Mandelbrot es el conjunto de los números complejos z tales que la sucesión definida por
) está acotada (algunos autores llaman conjunto de Julia a la frontera de J(c)). El conjunto de Mandelbrot es el conjunto de los números complejos z tales que la sucesión definida por 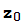 =0,
=0, 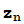 =
=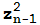 +z=
+z=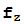 (
(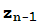 ) está acotada. En otros términos, el conjunto de Mandelbrot es el conjunto de los números complejos z tales que 0∈J(z).
) está acotada. En otros términos, el conjunto de Mandelbrot es el conjunto de los números complejos z tales que 0∈J(z).
Para representar la sucesión 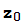 =z,
=z, 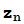 =
=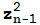 +c=
+c=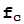 (
(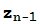 ) suele usarse la notación
) suele usarse la notación 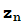 =
=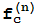 (z), con el convenio de que
(z), con el convenio de que 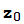 =
=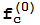 (z)=z. Esta sucesión se llama la órbita de z por
(z)=z. Esta sucesión se llama la órbita de z por 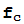 y sus elementos se obtienen iterando sucesivamente la función
y sus elementos se obtienen iterando sucesivamente la función 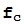 partiendo del valor inicial z. La notación
partiendo del valor inicial z. La notación 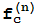 representa la composición de la función
representa la composición de la función 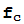 consigo misma n veces.
consigo misma n veces.
Ejercicio 1 Describe el conjunto de Julia correspondiente a c=0.
Ejercicio 2 Prueba que si |z|≥|c|>2 entonces z ∉J(c).
Ejercicio 3 Prueba que si |z|>2 entonces z no está en el conjunto de Mandelbrot. Deduce que si z está en el conjunto de Mandelbrot entonces todos los términos de la sucesión 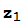 =0,
=0, 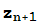 =
=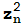 +z están en el disco |z|≤2.
+z están en el disco |z|≤2.
Ejercicio 4 Prueba que el disco |z|≤1/4 está contenido en el conjunto de Mandelbrot.
Ejercicio 5 Si |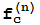 (z)|>max{|c|,2} para algún n≥0 entonces z ∉J(c). En particular, para |c|≤2 el conjunto J(c) está contenido en el disco |z|≤2.
(z)|>max{|c|,2} para algún n≥0 entonces z ∉J(c). En particular, para |c|≤2 el conjunto J(c) está contenido en el disco |z|≤2.
Los conjuntos de Julia y de Mandelbrot se representan con facilidad. El siguiente código procede de la revista Mathematica Journal.
In[16]:=
![JuliaFunction = Compile[{{z, _Complex}, {c, _Complex}}, Module[{w, k = 0}, w = z ; While[Abs[w] ≤2. && k≤35, w = w^2 + c ; k = k + 1] ; k] ] ;](HTMLFiles/index_79.gif)
Este código define una función "JuliaFunction[z,c]" que calcula términos de la órbita de z por  . El proceso se detiene si se encuentra un término de dicha órbita con módulo mayor que 2 y en otro caso continúa hasta calcular el término 35 de la sucesión. Observa que la salida de esta función es el número de iteraciones que realiza más una. Si z∈ J(c) entonces -JuliaFunction[z,c]=36, y si -JuliaFunction[z,c]<36 se tiene que z ∉J(c). Es posible que para algunos valores "raros" de z sean necesarias más de 35 iteraciones para saber si están o no en el conjunto de Julia, para tales valores podría ocurrir que Function[z,c]=36 pero z ∉J(c). El conjunto de estos valores "raros" es tan pequeño que no afecta realmente al aspecto final del conjunto.
. El proceso se detiene si se encuentra un término de dicha órbita con módulo mayor que 2 y en otro caso continúa hasta calcular el término 35 de la sucesión. Observa que la salida de esta función es el número de iteraciones que realiza más una. Si z∈ J(c) entonces -JuliaFunction[z,c]=36, y si -JuliaFunction[z,c]<36 se tiene que z ∉J(c). Es posible que para algunos valores "raros" de z sean necesarias más de 35 iteraciones para saber si están o no en el conjunto de Julia, para tales valores podría ocurrir que Function[z,c]=36 pero z ∉J(c). El conjunto de estos valores "raros" es tan pequeño que no afecta realmente al aspecto final del conjunto.
Calculemos los valores de "JuliaFunction[x+yI,-1]" en cada uno de los puntos (x,y) del retículo siguiente.
In[17]:=
![ListPlot[Flatten[Table[{x, y}, {y, -1.1, 1.1, .1}, {x, -1.5, 1.5, .1}], 1]] ;](HTMLFiles/index_81.gif)
![[Graphics:HTMLFiles/index_82.gif]](HTMLFiles/index_82.gif)
In[18]:=
![datos = Table[JuliaFunction[x + y I, -1], {y, -1.1, 1.1, .1}, {x, -1.5, 1.5, .1}]](HTMLFiles/index_83.gif)
Out[18]=
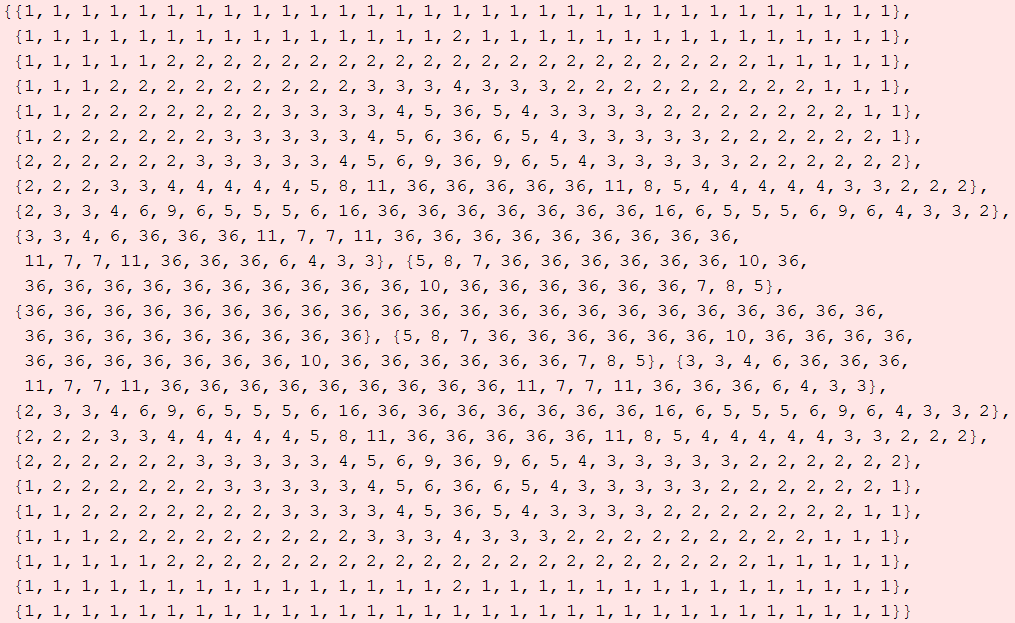
Podemos asignar un color a cada punto (x,y) según cuál sea el valor en dicho punto de la función JuliaFunction[x+yI,-1]. Es importante que entiendas cómo Mathematica asigna colores. Recuerda que la función "Hue" es periódica con período 1, es decir, Hue[x]=Hue[x+1]. Aquí puedes ver cómo asigna colores dicha función.
In[19]:=
![Show[Graphics[({Hue[#], Rectangle[{#, 0}, {#1 + .1, 1}]} &)/@Range[0, 2.5, .1], AspectRatio→Automatic]] ;](HTMLFiles/index_85.gif)
![[Graphics:HTMLFiles/index_86.gif]](HTMLFiles/index_86.gif)
Usemos "ListDensityPlot" para representar la tabla de valores, que hemos llamado "datos", antes obtenida. Como el valor de JuliaFunction[x+yI,-1] es siempre un número natural, se tiene que Hue[JuliaFunction[x+yI,-1]]=Hue[0]. Para evitar asignar a todos los puntos el mismo color, Mathematica hace una reducción a escala de los valores de la función JuliaFunction[x+yI,-1] antes de aplicar la función "Hue". Concretamente, en el caso que nos ocupa, el color que Mathematica asigna al punto (x,y) es Hue[JuliaFunction[x+yI,-1]/36]. Por ello los puntos en rojo están en el conjunto de Julia aunque también puntos alejados de dicho conjunto, por ejemplo aquellos en los que JuliaFunction[x+yI,-1]=1, se representan en un color rojizo pues Hue[1/36] es parecido a Hue[0]=Hue[1].
In[20]:=
![ListDensityPlot[datos, ColorFunction→Hue] ;](HTMLFiles/index_87.gif)
![[Graphics:HTMLFiles/index_88.gif]](HTMLFiles/index_88.gif)
Observa la diferencia entre la gráfica antes obtenida y la que sigue en la que hemos modificado la función de color de forma que distinga mejor los puntos del conjunto de Julia.
In[21]:=
![ListDensityPlot[datos, ColorFunction→ (Hue[If[#≥7, #/36, #/12]] &), ColorFunctionScaling→False] ;](HTMLFiles/index_89.gif)
![[Graphics:HTMLFiles/index_90.gif]](HTMLFiles/index_90.gif)
Hagamos lo mismo pero con más puntos. Es cómodo definir una función "datosjulia" como sigue.
In[22]:=
![Clear[datos] ;](HTMLFiles/index_91.gif)
![datosjulia[c_, inc_] := datosjulia[c, inc] = Table[JuliaFunction[x + y I, c], {y, -1.1, 1.1, inc}, {x, -1.5, 1.5, inc}]](HTMLFiles/index_92.gif)
Ahora representamos datos[-1,0.005] (si tu ordenador es lento, o eres muy impaciente, sustituye el incremento 0.005 por 0.01).
In[24]:=

![[Graphics:HTMLFiles/index_94.gif]](HTMLFiles/index_94.gif)
Exactamente lo mismo puede conseguirse directamente con el comando "DensityPlot".
In[25]:=

![[Graphics:HTMLFiles/index_96.gif]](HTMLFiles/index_96.gif)
La ventaja de proceder como antes es que Mathematica recuerda la lista "datosjulia[-1,0.005]" y, si queremos, podemos volver a representarla cambiando, por ejemplo, la función de color sin necesidad de volver a obtener los datos. Compruébalo.
In[26]:=

![[Graphics:HTMLFiles/index_98.gif]](HTMLFiles/index_98.gif)
Te sugiero que representes los conjuntos de Julia para valores de c igual a -0.5, 0.360284 + 0.100376 i, -0.122 + 0.745 i .
In[27]:=

![[Graphics:HTMLFiles/index_100.gif]](HTMLFiles/index_100.gif)
El siguiente código genera el conjunto de Mandelbrot.
In[28]:=
![MandelbrotFunction = Compile[{{z, _Complex}}, Module[{w, k = 0}, w = z ; While[Abs[w] ≤2. && k≤50, w = w^2 + z ; k = k + 1] ; k] ] ;](HTMLFiles/index_101.gif)
Te recuerdo otra vez que si tu ordenador es lento, o eres muy impaciente, sustituye el incremento 0.005 por 0.01 antes de evaluar la siguiente celda.
In[29]:=
![datosmandelbrot = Table[MandelbrotFunction[x + y I], {y, -1.15, 1.15, .005}, {x, -2., 0.55, .005}] ;](HTMLFiles/index_102.gif)
In[30]:=
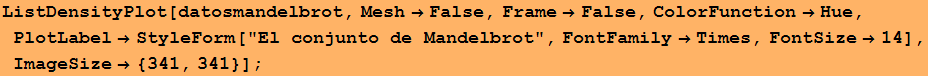
![[Graphics:HTMLFiles/index_104.gif]](HTMLFiles/index_104.gif)
Fractales maravillosos
Cambiemos la función de color para ver su efecto en el conjunto de Mandelbrot.
In[31]:=

![[Graphics:HTMLFiles/index_106.gif]](HTMLFiles/index_106.gif)
Con una pequeña modificación en los códigos anteriores puedes conseguir gráficos sorprendentes. La modificación consiste en pedirle a la función que nos devuelva el módulo del valor de la última iteración.
In[32]:=
![JuliaFunctionNew = Compile[{{z, _Complex}, {c, _Complex}}, Module[{w, k = 0}, w = z ; While[Abs[w] ≤2. && k≤35, w = w^2 + c ; k = k + 1] ; Abs[w]] ] ;](HTMLFiles/index_107.gif)
In[33]:=
![datosjulianew[c_, inc_] := datosjulianew[c, inc] = Table[JuliaFunctionNew[x + y I, c], {y, -1.5, 1.5, inc}, {x, -1.3, 1.3, inc}]](HTMLFiles/index_108.gif)
In[34]:=

![[Graphics:HTMLFiles/index_110.gif]](HTMLFiles/index_110.gif)
In[35]:=
![MandelbrotFunctionNew = Compile[{{z, _Complex}}, Module[{w, k = 0}, w = z ; While[Abs[w] ≤2. && k≤50, w = w^2 + z ; k = k + 1] ; Abs[w]] ] ;](HTMLFiles/index_111.gif)
In[36]:=
![datosmandelbrotnew = Table[MandelbrotFunctionNew[x + y I], {y, -1.15, 1.15, 0.005}, {x, -2., 0.55, 0.005}] ;](HTMLFiles/index_112.gif)
In[37]:=

![[Graphics:HTMLFiles/index_114.gif]](HTMLFiles/index_114.gif)
Observa el efecto de un cambio en la función de color.
In[38]:=
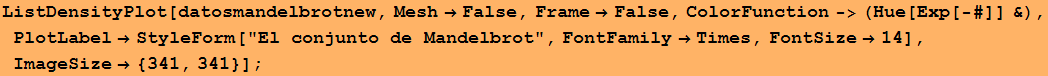
![[Graphics:HTMLFiles/index_116.gif]](HTMLFiles/index_116.gif)
Para terminar, volvamos al comienzo pero sustituyendo el polinomio 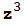 +1 por
+1 por 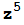 +1 y cambiando un poco el código.
+1 y cambiando un poco el código.
In[39]:=
![NewtonAproxNew = Compile[{{z, _Complex}}, Module[{w, k = 0}, w = z ; While[Abs[w^5 + 1] >0.001 && k≤50 && w≠0, w = (-1 + 4w^5)/(5 w^4) ; k = k + 1] ; k]] ;](HTMLFiles/index_119.gif)
In[40]:=
![datospolinomionew = Table[NewtonAproxNew[x + y ], {y, -2, 2, .00345}, {x, -2, 2, .00877}] ;](HTMLFiles/index_120.gif)
In[41]:=
![ListDensityPlot[datospolinomionew, Mesh→False, Frame→False, ColorFunction→ (Hue[1 - #] &), ImageSize→ {383, 383}] ;](HTMLFiles/index_121.gif)
![[Graphics:HTMLFiles/index_122.gif]](HTMLFiles/index_122.gif)
¡Qué maravilla! ¿Quién ha dicho que las matemáticas no son hermosas?
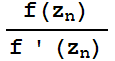 . Si dicha sucesión converge, su límite es una solución de la ecuación f(z)=0. Naturalmente, cuando hay más de una solución, la elección del valor inicial determina a cuál de ellas converge el proceso.
. Si dicha sucesión converge, su límite es una solución de la ecuación f(z)=0. Naturalmente, cuando hay más de una solución, la elección del valor inicial determina a cuál de ellas converge el proceso. 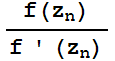
![z[n_] := z[n] = z[n - 1] - (z[n - 1]^2 + 1)/(2 z[n - 1]) ;](HTMLFiles/index_17.gif)
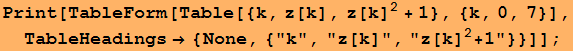
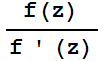
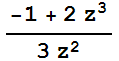
![NewtonAprox = Compile[{{z, _Complex}}, Module[{w, k = 0}, w = z ; While[Abs[w^3 + 1] >0.001 && k≤50 && w≠0, w = (-1 + 2w^3)/(3 w^2) ; k = k + 1] ; w]] ;](HTMLFiles/index_33.gif)



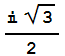
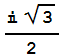
![DensityPlot[NewtonColorAprox[x + y I], {x, -2, 2.}, {y, -2, 2}, PlotPoints→500, Mesh→False, AspectRatio→1, ColorFunction→Hue] ;](HTMLFiles/index_43.gif)
![[Graphics:HTMLFiles/index_44.gif]](HTMLFiles/index_44.gif)
![DensityPlot[NewtonColorAprox[x + y I], {x, -.6, 0.01}, {y, 0.01, .8}, PlotPoints→200, Mesh→False, AspectRatio→1, ColorFunction→Hue] ;](HTMLFiles/index_45.gif)
![[Graphics:HTMLFiles/index_46.gif]](HTMLFiles/index_46.gif)
![DensityPlot[NewtonColorAprox[x + y I], {x, -.154, -0.088}, {y, 0.55, .7}, PlotPoints→200, Mesh→False, AspectRatio→1, ColorFunction→Hue] ;](HTMLFiles/index_47.gif)
![[Graphics:HTMLFiles/index_48.gif]](HTMLFiles/index_48.gif)
![JuliaFunction = Compile[{{z, _Complex}, {c, _Complex}}, Module[{w, k = 0}, w = z ; While[Abs[w] ≤2. && k≤35, w = w^2 + c ; k = k + 1] ; k] ] ;](HTMLFiles/index_79.gif)
![[Graphics:HTMLFiles/index_82.gif]](HTMLFiles/index_82.gif)

![Show[Graphics[({Hue[#], Rectangle[{#, 0}, {#1 + .1, 1}]} &)/@Range[0, 2.5, .1], AspectRatio→Automatic]] ;](HTMLFiles/index_85.gif)
![[Graphics:HTMLFiles/index_86.gif]](HTMLFiles/index_86.gif)
![[Graphics:HTMLFiles/index_88.gif]](HTMLFiles/index_88.gif)
![ListDensityPlot[datos, ColorFunction→ (Hue[If[#≥7, #/36, #/12]] &), ColorFunctionScaling→False] ;](HTMLFiles/index_89.gif)
![[Graphics:HTMLFiles/index_90.gif]](HTMLFiles/index_90.gif)
![datosjulia[c_, inc_] := datosjulia[c, inc] = Table[JuliaFunction[x + y I, c], {y, -1.1, 1.1, inc}, {x, -1.5, 1.5, inc}]](HTMLFiles/index_92.gif)

![[Graphics:HTMLFiles/index_94.gif]](HTMLFiles/index_94.gif)

![[Graphics:HTMLFiles/index_96.gif]](HTMLFiles/index_96.gif)

![[Graphics:HTMLFiles/index_98.gif]](HTMLFiles/index_98.gif)

![[Graphics:HTMLFiles/index_100.gif]](HTMLFiles/index_100.gif)
![MandelbrotFunction = Compile[{{z, _Complex}}, Module[{w, k = 0}, w = z ; While[Abs[w] ≤2. && k≤50, w = w^2 + z ; k = k + 1] ; k] ] ;](HTMLFiles/index_101.gif)
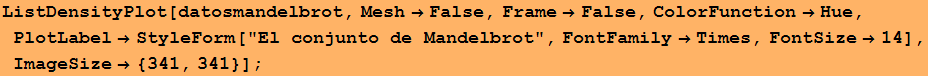
![[Graphics:HTMLFiles/index_104.gif]](HTMLFiles/index_104.gif)

![[Graphics:HTMLFiles/index_106.gif]](HTMLFiles/index_106.gif)
![JuliaFunctionNew = Compile[{{z, _Complex}, {c, _Complex}}, Module[{w, k = 0}, w = z ; While[Abs[w] ≤2. && k≤35, w = w^2 + c ; k = k + 1] ; Abs[w]] ] ;](HTMLFiles/index_107.gif)
![datosjulianew[c_, inc_] := datosjulianew[c, inc] = Table[JuliaFunctionNew[x + y I, c], {y, -1.5, 1.5, inc}, {x, -1.3, 1.3, inc}]](HTMLFiles/index_108.gif)

![[Graphics:HTMLFiles/index_110.gif]](HTMLFiles/index_110.gif)
![MandelbrotFunctionNew = Compile[{{z, _Complex}}, Module[{w, k = 0}, w = z ; While[Abs[w] ≤2. && k≤50, w = w^2 + z ; k = k + 1] ; Abs[w]] ] ;](HTMLFiles/index_111.gif)
![datosmandelbrotnew = Table[MandelbrotFunctionNew[x + y I], {y, -1.15, 1.15, 0.005}, {x, -2., 0.55, 0.005}] ;](HTMLFiles/index_112.gif)

![[Graphics:HTMLFiles/index_114.gif]](HTMLFiles/index_114.gif)
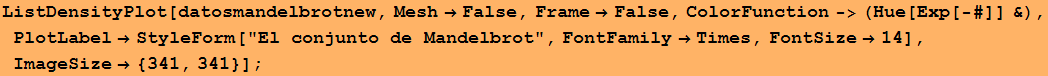
![[Graphics:HTMLFiles/index_116.gif]](HTMLFiles/index_116.gif)
![NewtonAproxNew = Compile[{{z, _Complex}}, Module[{w, k = 0}, w = z ; While[Abs[w^5 + 1] >0.001 && k≤50 && w≠0, w = (-1 + 4w^5)/(5 w^4) ; k = k + 1] ; k]] ;](HTMLFiles/index_119.gif)
![ListDensityPlot[datospolinomionew, Mesh→False, Frame→False, ColorFunction→ (Hue[1 - #] &), ImageSize→ {383, 383}] ;](HTMLFiles/index_121.gif)
![[Graphics:HTMLFiles/index_122.gif]](HTMLFiles/index_122.gif)