Principio de Cavalieri. El área de una región plana es igual a la integral de las longitudes de sus secciones por rectas paralelas a una recta dada.
Veamos cómo se aplica este principio en algunos casos concretos.
Aplicaciones de las integrales simples
Universidad de Granada
Departamento de Análisis Matemático
Francisco Javier Pérez González
Introducción
Este cuaderno debe ejecutarse con las versiones 4 o 5 de Mathematica.
Con una integral puedes calcular magnitudes tan diversas como áreas, volúmenes, longitudes de curvas, el trabajo realizado por una fuerza, el punto de equilibrio y la masa de un sólido, momentos de inercia, el campo electrostático producido por una distribución de cargas, el flujo de una fluido a través de una superficie y muchas más.
Lo que debes aprender en este cuaderno.
Calcular áreas de recintos en el plano limitados por varias curvas.
Calcular áreas de curvas cerradas dadas por sus ecuaciones paramétricas.
Calcular longitudes de curvas.
Calcular volúmenes de cuerpos de revolución por el método de los discos, de las arandelas y de los tubos.
Calcular áreas de superficies de revolución.
Para trabajar en este cuaderno debes evaluar primero ( Kernel → Evaluation→ Evaluate Initialization ) las celdas de inicialización que siguen.
Cálculo de áreas planas
Te recuerdo que si f:[a,b]→R es una función continua, representamos por G(f,a,b) la región del plano comprendida entre la curva y= f(x), el eje de abscisas y las rectas y=a, y=b. Como sabes, el área de dicha región viene dada por λ(G(f,a,b))=![]() |f(x)|dx (no suponemos que f sea positiva). Es interesante interpretar la integral que proporciona el área de la siguiente forma. Observa que |f(x)| es la longitud del segmento intersección de G(f,a,b) con la recta vertical que pasa por (x,0), es decir, |f(x)| es la longitud de la sección vertical de G(f,a,b) por el punto (x,0), y el área de la región G(f,a,b) es igual a la integral de las longitudes de sus secciones. Intuitivamente: integrando longitudes obtenemos áreas. Como el área es invariante por rotaciones, este resultado es también válido si consideramos secciones por rectas paralelas a una recta cualquiera dada. Deducimos así el siguiente resultado.
|f(x)|dx (no suponemos que f sea positiva). Es interesante interpretar la integral que proporciona el área de la siguiente forma. Observa que |f(x)| es la longitud del segmento intersección de G(f,a,b) con la recta vertical que pasa por (x,0), es decir, |f(x)| es la longitud de la sección vertical de G(f,a,b) por el punto (x,0), y el área de la región G(f,a,b) es igual a la integral de las longitudes de sus secciones. Intuitivamente: integrando longitudes obtenemos áreas. Como el área es invariante por rotaciones, este resultado es también válido si consideramos secciones por rectas paralelas a una recta cualquiera dada. Deducimos así el siguiente resultado.
Principio de Cavalieri. El área de una región plana es igual a la integral de las longitudes de sus secciones por rectas paralelas a una recta dada.
Veamos cómo se aplica este principio en algunos casos concretos.
Área entre dos curvas
Regiones de tipo I
Supongamos que f,g:[a,b]→R son funciones continuas y llamemos Ω a la región del plano comprendida entre las curvas y= f(x) e y=g(x) para x ε [a,b]. Se dice que Ω es una región de tipo I. Puedes representar gráficamente dicha región con la orden "tipo1[{f,g},{x,a,b},opts]" (que admite opciones como "Plot"). Experimenta con distintas funciones. Aquí tienes unos ejemplos.
In[46]:=
![]()
![[Graphics:HTMLFiles/aplicaciones_integral_24.gif]](HTMLFiles/aplicaciones_integral_24.gif)
In[47]:=
![]()
![[Graphics:HTMLFiles/aplicaciones_integral_26.gif]](HTMLFiles/aplicaciones_integral_26.gif)
In[48]:=
![]()
![[Graphics:HTMLFiles/aplicaciones_integral_28.gif]](HTMLFiles/aplicaciones_integral_28.gif)
Es evidente que las longitudes de las secciones verticales de Ω son iguales a |f(x)-g(x)| por lo que su área viene dada por
![]()
Observa que esta integral expresa el área de Ω como límite de las sumas de Riemann ![]() |f(
|f(![]() )-g(
)-g(![]() )|(
)|(![]() -
-![]() ), lo que tiene una sencilla interpretación que puedes visualizar con la orden "tipo1sup[{f,g},{x,a,b,n},opts]" (admite opciones como "Plot") que representa aproximaciones superiores al área de Ω dividiendo [a,b] en n subintervalos [
), lo que tiene una sencilla interpretación que puedes visualizar con la orden "tipo1sup[{f,g},{x,a,b,n},opts]" (admite opciones como "Plot") que representa aproximaciones superiores al área de Ω dividiendo [a,b] en n subintervalos [![]() ,
,![]() ] y eligiendo en cada uno de ellos el punto
] y eligiendo en cada uno de ellos el punto ![]() ε [
ε [![]() ,
,![]() ] en el que la función|f-g| alcanza su máximo absoluto en dicho subintervalo. Significado análogo tiene el comando "tipo1inf[{f,g},{x,a,b,n},opts]". Prueba con distintas funciones. Los siguientes ejemplos son ilustrativos.
] en el que la función|f-g| alcanza su máximo absoluto en dicho subintervalo. Significado análogo tiene el comando "tipo1inf[{f,g},{x,a,b,n},opts]". Prueba con distintas funciones. Los siguientes ejemplos son ilustrativos.
In[49]:=
![]()
![[Graphics:HTMLFiles/aplicaciones_integral_41.gif]](HTMLFiles/aplicaciones_integral_41.gif)
In[50]:=
![]()
![[Graphics:HTMLFiles/aplicaciones_integral_43.gif]](HTMLFiles/aplicaciones_integral_43.gif)
Las siguientes animaciones muestarn cómo las aproximaciones van mejorando conforme aumenta el número de intervalos de la partición.
![]()
![[Graphics:HTMLFiles/aplicaciones_integral_54.gif]](pescado1.gif)
![]()
![[Graphics:HTMLFiles/aplicaciones_integral_65.gif]](pescado2.gif)
En la práctica, es frecuente describir una región de tipo I como "la región comprendida entre las curvas y= f(x) e y=g(x)" sin precisar el intervalo de la variable x. En estos casos, se entiende que se trata de la región acotada comprendidad entre las dos gráficas; la cual debe determinarse calculando los puntos de intersección de las mismas, es decir, resolviendo la ecuación f(x)=g(x) lo que también nos proporciona los límites de integración a y b.
Cuando la función f - g no tiene signo constante en el intervalo [a,b], para calcular la integral ![]() |f(x)-g(x)|dx se descompone dicho intervalo en intervalos en los que la función f - g es siempre positiva o siempre negativa, lo que permite quitar el valor absoluto en el integrando.
|f(x)-g(x)|dx se descompone dicho intervalo en intervalos en los que la función f - g es siempre positiva o siempre negativa, lo que permite quitar el valor absoluto en el integrando.
A veces interesa expresar una región de tipo I como unión de dos o más regiones de tipo I disjuntas y más sencillas, entonces su área es la suma de las áreas de cada una de dichas regiones.
Ejemplo 1
Calcular el área de la region Ω comprendida entre la parábola y=-![]() -2x+10 y la recta y=2x-1.
-2x+10 y la recta y=2x-1.
Calculamos los puntos donde se cortan la parábola y la recta.
In[59]:=
![]()
Out[59]=
![]()
Representaremos la región Ω. Puedes usar para ello la orden "Plot[ ]".
In[60]:=
![]()
![[Graphics:HTMLFiles/aplicaciones_integral_71.gif]](HTMLFiles/aplicaciones_integral_71.gif)
También podemos usar "FilledPlot[ ]" que dibuja en azul la zona comprendida entre la recta y la parábola.
In[61]:=
![]()
![[Graphics:HTMLFiles/aplicaciones_integral_73.gif]](HTMLFiles/aplicaciones_integral_73.gif)
Es claro que para x ε [-2-![]() ,-2+
,-2+![]() ] la parábola está por encima de la recta. Por tanto, el área de Ω viene dada por
] la parábola está por encima de la recta. Por tanto, el área de Ω viene dada por
In[62]:=
![]()
![]()
Out[62]=
![]()
Ejemplo 2
Calcular el área de la región Ω comprendida entre la parábola ![]() =x y la recta y=x-2.
=x y la recta y=x-2.
Calculemos los puntos de corte de la recta y=x-2 con la parábola ![]() =x.
=x.
In[64]:=
![]()
Out[64]=
![]()
In[65]:=
![]()
![[Graphics:HTMLFiles/aplicaciones_integral_84.gif]](HTMLFiles/aplicaciones_integral_84.gif)
Fíjate en que la parábola ![]() =x es la unión de las dos curvas y=
=x es la unión de las dos curvas y=![]() y y=-
y y=-![]() , por lo que la frontera de Ω está determinada por dichas curvas y la recta y=x-2. Es claro que Ω es unión de dos regiones de tipo I.
, por lo que la frontera de Ω está determinada por dichas curvas y la recta y=x-2. Es claro que Ω es unión de dos regiones de tipo I.
In[66]:=
![]()
![]()
![]()
![[Graphics:HTMLFiles/aplicaciones_integral_91.gif]](HTMLFiles/aplicaciones_integral_91.gif)
Tenemos que el área de Ω viene dada por λ(Ω)=λ(Ω1)+λ(Ω2)=![]() (
(![]() -(-
-(-![]() ))dx +
))dx + ![]() (
(![]() -(x-2))dx.
-(x-2))dx.
In[69]:=
![]()
Out[69]=
![]()
Observa que Ω es ella misma una región de tipo I definida por las funciones f,g:[0,4]→R dadas por g(x)=![]() y f(x)=-
y f(x)=-![]() , para 0≤ x≤ 1, f(x)=x-2, para 1≤ x≤ 4.
, para 0≤ x≤ 1, f(x)=x-2, para 1≤ x≤ 4.
In[70]:=
![]()
![]()
![]()
![]()
![]()
![[Graphics:HTMLFiles/aplicaciones_integral_106.gif]](HTMLFiles/aplicaciones_integral_106.gif)
Regiones de tipo II
Supongamos que f,g:[a,b]→R son funciones continuas y llamemos Ω a la región del plano comprendida entre las curvas x= f(y) y x=g(y) para y ε [a,b]. Se dice que Ω es una región de tipo II. Puedes representar gráficamente una región de tipo II con la orden "tipo2[{f,g},{y,a,b},opts]" (que admite opciones como "Show"). Experimenta con distintas funciones. Observa que las regiones de tipo II son las simétricas de las regiones de tipo I respecto de la recta y=x. Es decir, una región de tipo II es una región de tipo I vista desde el eje de ordenadas. Aquí tienes unos ejemplos.
In[75]:=
![]()
![[Graphics:HTMLFiles/aplicaciones_integral_108.gif]](HTMLFiles/aplicaciones_integral_108.gif)
In[76]:=
![]()
![[Graphics:HTMLFiles/aplicaciones_integral_110.gif]](HTMLFiles/aplicaciones_integral_110.gif)
Es evidente que las longitudes de las secciones horizontales de Ω son iguales a |f(y)-g(y)| por lo que su área viene dada por
![]()
Observa que esta integral expresa el área de Ω como límite de las sumas de Riemann ![]() |f(
|f(![]() )-g(
)-g(![]() )|(
)|(![]() -
-![]() ), lo que tiene una sencilla interpretación que puedes visualizar con la orden "tipo2sup[{f,g},{y,a,b,n},opts]" (admite opciones como "Show") que representa aproximaciones superiores al área de Ω dividiendo el intervalo [a,b] del eje de ordenadas en n subintervalos [
), lo que tiene una sencilla interpretación que puedes visualizar con la orden "tipo2sup[{f,g},{y,a,b,n},opts]" (admite opciones como "Show") que representa aproximaciones superiores al área de Ω dividiendo el intervalo [a,b] del eje de ordenadas en n subintervalos [![]() ,
,![]() ] y eligiendo en cada uno de ellos el punto
] y eligiendo en cada uno de ellos el punto ![]() ε [
ε [![]() ,
,![]() ] en el que la función|f-g| alcanza su máximo absoluto en dicho subintervalo. Significado análogo tiene el comando "tipo1inf[{f,g},{y,a,b,n},opts]". Prueba con distintas funciones. Los siguientes ejemplos son ilustrativos.
] en el que la función|f-g| alcanza su máximo absoluto en dicho subintervalo. Significado análogo tiene el comando "tipo1inf[{f,g},{y,a,b,n},opts]". Prueba con distintas funciones. Los siguientes ejemplos son ilustrativos.
In[77]:=
![]()
![[Graphics:HTMLFiles/aplicaciones_integral_123.gif]](HTMLFiles/aplicaciones_integral_123.gif)
In[78]:=
![]()
![[Graphics:HTMLFiles/aplicaciones_integral_125.gif]](HTMLFiles/aplicaciones_integral_125.gif)
Las siguientes animaciones muestarn cómo las aproximaciones van mejorando conforme aumenta el número de intervalos de la partición.
![]()
![[Graphics:HTMLFiles/aplicaciones_integral_136.gif]](pescado1vert.gif)
![]()
![[Graphics:HTMLFiles/aplicaciones_integral_147.gif]](pescado2vert.gif)
Es importante advertir que la distinción entre regiones de tipo I y de tipo II es tan sólo una cuestión de conveniencia. No son conjuntos de distinta naturaleza sino formas distintas de describir un conjunto. En la prática te vas a encontrar siempre con regiones que puedes considerar tanto de tipo I como de tipo II y deberás elegir la descripción que más facilite el cálculo de la correspondiente integral. De todas formas, no debes olvidar que basta cambiar la variable x por la variable y para convertir una región de tipo II en otra de tipo I; por tanto, si en un ejercicio resulta conveniente considerar la región cuya área quieres calcular como una región de tipo II y te encuentras más cómodo trabajando con regiones de tipo I, ya sabes lo que tienes que hacer.
En la práctica, es frecuente describir una región de tipo II como "la región comprendida entre las curvas x=f(y) y x=g(y)" sin precisar el intervalo de la variable y. En estos casos, se entiende que se trata de la región acotada comprendidad entre las dos curvas; la cual debe determinarse calculando los puntos de intersección de las mismas, es decir, resolviendo la ecuación f(y)=g(y) lo que también nos proporciona los límites de integración a y b.
Cuando la función f - g no tiene signo constante en el intervalo [a,b], para calcular la integral ![]() |f(y)-g(y)|dy se descompone dicho intervalo en intervalos en los que la función f - g es siempre positiva o siempre negativa, lo que permite quitar el valor absoluto en el integrando.
|f(y)-g(y)|dy se descompone dicho intervalo en intervalos en los que la función f - g es siempre positiva o siempre negativa, lo que permite quitar el valor absoluto en el integrando.
A veces interesa expresar una región de tipo II como unión de dos o más regiones de tipo II disjuntas y más sencillas, entonces su área es la suma de las áreas de cada una de dichas regiones.
Aunque las regiones que hemos considerado antes son acotadas, la idea de región no acotada de tipo I y de tipo II se entiende por sí sola y no precisa nueva definición. Los resultados anteriores se extienden fácilmente al caso de regiones no acotadas de tipo I y de tipo II, la única diferencia es que ahora las áreas vendrán dadas por integrales de funciones no acotadas o en intervalos no acotados. Como ya debes de saber, para calcular dichas integrales tienes que evaluar una primitiva y calcular su límite.
Ejemplo 3
Calcular el área de la región Ω comprendida entre la parábola ![]() =x y la recta y=x-2.
=x y la recta y=x-2.
Se trata del mismo ejercicio considerado en el ejemplo 2. Recuerda que, para calcular el área, expresábamos Ω como unión de dos regiones de tipo I. De hecho, la propia región Ω es de tipo I. Sin embargo, los cálculos son más sencillos si consideramos Ω como la región de tipo II limitada por las curvas x=![]() y x=y+2 cuyos puntos de intersección se obtiene para y=-1, y=2.
y x=y+2 cuyos puntos de intersección se obtiene para y=-1, y=2.
In[87]:=
![]()
![[Graphics:HTMLFiles/aplicaciones_integral_152.gif]](HTMLFiles/aplicaciones_integral_152.gif)
Por tanto, el área de Ω viene dada por λ(Ω)=![]() (y+2-
(y+2-![]() )dy.
)dy.
In[88]:=
![]()
Out[88]=
![]()
Si quieres ver Ω como una región de tipo I más sencilla que la considerada en el ejemplo 2, puedes simetrizar su gráfica como sigue.
In[89]:=
![]()
![[Graphics:HTMLFiles/aplicaciones_integral_158.gif]](HTMLFiles/aplicaciones_integral_158.gif)
Aunque la región así obtenida no es la misma Ω tiene, sin embargo, igual área que Ω pues ambas regiones se transforman una en otra por medio de una simetría respecto de la recta y=x.
Ejercicios
1 Calcula las áreas de las regiones del plano limitadas por las siguientes curvas.
a) x=12![]() -12
-12![]() y x=2
y x=2![]() -2y.
-2y.
b) y=-![]() -2x e y=
-2x e y=![]() -4, para -3≤ x≤ 1.
-4, para -3≤ x≤ 1.
c) y=![]() y x+y=2, con x≥ 0, y≥ 0.
y x+y=2, con x≥ 0, y≥ 0.
d) x+![]() =3 y 4x+
=3 y 4x+![]() =4.
=4.
e) y=![]() x, y=
x, y=![]() x, -π/4≤ x≤ π/4.
x, -π/4≤ x≤ π/4.
f) ![]() +
+![]() =1.
=1.
g) ![]() =x-3, y x=7.
=x-3, y x=7.
h) y=![]() +
+![]() +16x-4 y y=
+16x-4 y y=![]() +6
+6![]() +8x-4.
+8x-4.
i) y=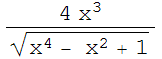 , y=
, y=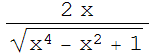 , 0≤ x≤ 1.
, 0≤ x≤ 1.
j) y=![]() , 0< x≤ e.
, 0< x≤ e.
k) ![]() =
=![]() , x=-1.
, x=-1.
l) y=x ![]() , y=
, y=![]()
![]() , x≥ 0.
, x≥ 0.
2 Calcula el área de la región limitada por la astroide ![]() +
+![]() =1.
=1.
In[90]:=
![]()
![[Graphics:HTMLFiles/aplicaciones_integral_187.gif]](HTMLFiles/aplicaciones_integral_187.gif)
3 Calcula el área de la región comprendida entre la cisoide ![]() =
=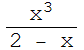 y su asíntota x=2.
y su asíntota x=2.
In[91]:=
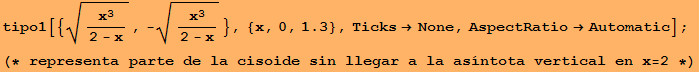
![[Graphics:HTMLFiles/aplicaciones_integral_191.gif]](HTMLFiles/aplicaciones_integral_191.gif)
4 Calcula el área de las dos partes en que la parábola ![]() =x divide al círculo
=x divide al círculo ![]() +
+![]() =8.
=8.
In[92]:=
![]()
![]()
![]()
![[Graphics:HTMLFiles/aplicaciones_integral_198.gif]](HTMLFiles/aplicaciones_integral_198.gif)
Curvas definidas por ecuaciones paramétricas
Seguramente te imaginas una curva en el plano como una línea continua que puede dibujarse de un trazo, sin levantar el lápiz del papel. Esa idea es esencialmente correcta. Las circunferencias, las elipses, las astroides son todas ellas curvas. Faltaría más. Ninguna de ellas puedes representarla por una igualdad de la forma y=f(x). Las curvas que pueden representarse por una ecuación cartesiana del tipo y=f(x) son curvas muy particulares pues son gráficas de funciones. No olvides que cuando dices "sea la curva dada por la ecuación y=f(x)" te estás refiriendo a la curva cuya imagen es el conjunto de puntos del plano {(x,y):x ε [a,b], y=f(x)}, es decir, a la gráfica de f. Si lo piensas un momento verás que muy pocas curvas son gráficas. Para que una curva sea una gráfica es necesario que cualquier recta vertical la corte a lo más en un solo punto; ninguna curva cerrada cumple esta condición. Precisamente entre las curvas cerradas se encuentran algunas de las curvas más intersantes, a ellas pertenecen los distintos tipos de óvalos y lemniscatas, las cardioides, y muchas más. Vamos a ver ahora una forma de representar curvas planas mucho más general que las ecuaciones cartesianas del tipo y=f(x) que sólo sirven para representar curvas que también son gráficas.
Para empezar, consideremos una curva que viene dada por una ecuación cartesiana de la forma y=f(x) donde a≤ x≤ y. Nuestra curva es, por tanto, la imagen de la aplicación γ:[a,b] → ![]() definida por γ(x)=(x,f(x)) para todo x ε [a,b]. Intuitavamente, cuando x recorre el intervalo [a,b], el punto (x,f(x)) recorre la curva. Es fácil generalizar esta situación sin perder la idea intuitiva de curva. Lo esencial es que podamos describir las coordendas de los puntos de la curva como funciones continuas de un parámetro. En la situación que estamos considerando se tiene que y=f(x) ,es decir, la segunda coordenada es función continua de la primera. La generalización consiste en que ambas coordenadas sean funciones continuas de un parámetro. Llegamos así a la definición siguiente.
definida por γ(x)=(x,f(x)) para todo x ε [a,b]. Intuitavamente, cuando x recorre el intervalo [a,b], el punto (x,f(x)) recorre la curva. Es fácil generalizar esta situación sin perder la idea intuitiva de curva. Lo esencial es que podamos describir las coordendas de los puntos de la curva como funciones continuas de un parámetro. En la situación que estamos considerando se tiene que y=f(x) ,es decir, la segunda coordenada es función continua de la primera. La generalización consiste en que ambas coordenadas sean funciones continuas de un parámetro. Llegamos así a la definición siguiente.
Definición. Una curva en el plano es una aplicación continua γ:[a,b] → ![]() . Si γ(t)=(x(t),y(t)) decimos que {
. Si γ(t)=(x(t),y(t)) decimos que {
son las ecuaciones parámetricas de la curva. El punto γ(a) es el origen y γ(b) el extremo de la curva. Si γ(a)=γ(b) se dice que la curva es cerrada. Se dice que una curva γ es simple si no se corta a sí misma, es decir, si para s,t ε [a,b] con t≠s se verifica que γ(t)≠γ(s). Una curva cerrada se llama simple si la función γ es inyectiva en ]a,b[.
x=x(t)
y=y(t)
Ejemplos
● La curva de ecuaciones paramétricas x=α+a cos t,y=β+b sen t para 0≤t≤ 2π, α>0,β>0 es una elipse de centro (α,β) y semiejes de longitudes a, b. Cuando a=b se trata de una círcunferencia.
In[95]:=
![]()
![[Graphics:HTMLFiles/aplicaciones_integral_202.gif]](HTMLFiles/aplicaciones_integral_202.gif)
● La curva de ecuaciones paramétricas x=r (t-sen t), y=r (1- cos t) para 0≤t≤ 2π es la cicloide. Es la curva que describiría una chincheta clavada en una rueda de radio r que avanza girando sin deslizar.
In[96]:=
![]()
![[Graphics:HTMLFiles/aplicaciones_integral_204.gif]](HTMLFiles/aplicaciones_integral_204.gif)
Para ver cómo se genera la cicloide ejecuta la siguiente celda
![]()
![]()
● La curva de ecuaciones paramétricas x=cos t (1+cos t), y=sen t (1+cos t) para 0≤t≤ 2π es una cardioide. Es la curva que describe un punto fijo del borde de un círculo que rueda sin deslizar sobre otro del mismo radio.
In[101]:=
![]()
![[Graphics:HTMLFiles/aplicaciones_integral_229.gif]](HTMLFiles/aplicaciones_integral_229.gif)
La ecuación cartesiana de la cardioide es ![]() =(
=(![]() +
+![]() ) 4
) 4 ![]() donde a es un parámetro positivo. Para ver cómo se genera la cardiode ejecuta la siguiente celda
donde a es un parámetro positivo. Para ver cómo se genera la cardiode ejecuta la siguiente celda
![]()
![[Graphics:HTMLFiles/aplicaciones_integral_256.gif]](cardioide.gif)
![]()
In[106]:=
![]()
![[Graphics:HTMLFiles/aplicaciones_integral_259.gif]](HTMLFiles/aplicaciones_integral_259.gif)
La ecuación cartesiana de la lemniscata es ![]() =
=![]() -
-![]() y se define como el lugar geométrico de los puntos del plano cuyo producto de distancias a dos puntos fijos es constante igual al cuadrado de la semidistancia entre dichos puntos. Observa que, a diferencia de las anteriores, la lemniscata no es una curva simple.
y se define como el lugar geométrico de los puntos del plano cuyo producto de distancias a dos puntos fijos es constante igual al cuadrado de la semidistancia entre dichos puntos. Observa que, a diferencia de las anteriores, la lemniscata no es una curva simple.
● Aquí tienes otro ejemplo de una curva que no es simple.
In[107]:=
![]()
![[Graphics:HTMLFiles/aplicaciones_integral_264.gif]](HTMLFiles/aplicaciones_integral_264.gif)
Cálculo del área de una región plana rodeada por una curva definida por ecuaciones paramétricas
Sea Ω la región rodeada por una curva cerrada simple γ(t)=(x(t),y(t)), (a≤t≤b) y supongamos que las funciones t→ x(t), t→ y(t) tienen primera derivada continua. Supongamos también que si, a medida que el parámetro t recorre el intervalo desde t=a hasta t=b, andamos sobre la curva siguiendo al punto γ(t) la región Ω queda a nuestar izquierda. En estas condiciones se verifica que el área de Ω viene dada por:
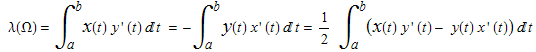
La igualdad entre las dos integrales se deduce fácilmente integrando por partes y teniendo en cuenta que por ser γ una curva cerrada se tiene que x(b)y(b)-x(a)y(a)=0. Si el sentido de recorrido de la curva es el opuesto al anterior de forma que al recorrerla la región Ω queda a la derecha debemos cambiar el signo en las integrales anteriores.
Ejemplos
![]()
Observa que al recorrer la curva la región Ω queda a la izquierda por lo que el área viene dada por:
In[108]:=
![]()
![]()
![]()
Out[110]=
![]()
● Calcular el área de la región Ω encerrada por un arco de la cicloide x(t)=r (t-sen t), y(t)=r (1- cos t), 0≤t≤2π, y el segmento que va de (2π r,0) a (0,0). Dicho segmento tiene como ecuaciones parametricas (u(t),v(t))=( -r t +4π r,0) donde 2π≤t≤4π.
Observa que al recorrer la curva la región Ω queda a la derecha por lo que el área viene dada por:
In[111]:=
![]()
![]()
![]()
![]()
![]()
Out[115]=
![]()
Ejercicios
5 Calcular el área encerrada por la cardioide x=cos t (1+cos t), y=sen t (1+cos t),0≤t≤ 2π.
Áreas planas en coordenadas polares
Dado un punto (x,y) ε ![]() , (x,y)≠ (0,0), hay un único par de números (ρ,θ) tales que 0<ρ, -π<θ≤π y que verifican las igualdades {
, (x,y)≠ (0,0), hay un único par de números (ρ,θ) tales que 0<ρ, -π<θ≤π y que verifican las igualdades {
. Dichos números se llaman coordenadas polares del punto (x,y) y vienen dados por ρ=
x=ρ cos θ
y= ρ sen θ
![]() ; θ=arctg
; θ=arctg![]() si x>0; θ=arctg
si x>0; θ=arctg![]() -π si x<0, y<0; θ=arctg
-π si x<0, y<0; θ=arctg![]() +π si x<0, y≥0; θ=π/2 si x=0, y>0; θ=-π/2 si x=0, y<0. El número θ se llama ángulo polar del vector (x,y) y el número ρ es la norma euclídea de dicho vector. La función "polares[{x,y}]" proporciona las coordenadas polares del punto de coordenadas cartesianas (x,y). La función "cartesianas[{ρ,θ}]" proporciona las coordenadas cartesianas del punto de coordenadas polares (ρ,θ). Practica un poco con estos comandos y observa cómo la función "ArcTan[x,y]" tiene en cuenta el cuadrante donde está el punto (x,y).
+π si x<0, y≥0; θ=π/2 si x=0, y>0; θ=-π/2 si x=0, y<0. El número θ se llama ángulo polar del vector (x,y) y el número ρ es la norma euclídea de dicho vector. La función "polares[{x,y}]" proporciona las coordenadas polares del punto de coordenadas cartesianas (x,y). La función "cartesianas[{ρ,θ}]" proporciona las coordenadas cartesianas del punto de coordenadas polares (ρ,θ). Practica un poco con estos comandos y observa cómo la función "ArcTan[x,y]" tiene en cuenta el cuadrante donde está el punto (x,y).
In[116]:=
![]()
![]()
Es importante advertir que en la definición anterior el intervalo ]-π,π] se puede sustituir por cualquier intervalo semiabierto I de longitud 2π lo que, naturalmente, implica modificar la definición de θ sumando o restando, según proceda, un múltiplo conveniente de 2π de manera que el ángulo polar esté en dicho intervalo I. Es frecuente considerar valores del ángulo polar en el intervalo [0,2π[. Salvo que se especifique otra cosa, entenderemos que el ángulo polar está en el intervalo ]-π,π].
La función "PolarPlot[f[θ],{θ, α, β}]" representa la curva cuya ecuación en coordenadas polares es ρ=f(θ), (α≤θ≤β). Es decir, representa el conjunto de puntos del plano cuyas coordenadas polares son (f(θ),θ) cuando θ ε [α,β]. Equivalentemente, se trata de la curva cuyas ecuaciones paramétricas son x(θ)=f(θ)cos(θ), y(θ)=f(θ)sen (θ), θ ε [α,β].
In[118]:=
![]()
![[Graphics:HTMLFiles/aplicaciones_integral_285.gif]](HTMLFiles/aplicaciones_integral_285.gif)
In[119]:=
![]()
![[Graphics:HTMLFiles/aplicaciones_integral_287.gif]](HTMLFiles/aplicaciones_integral_287.gif)
In[120]:=
![]()
![[Graphics:HTMLFiles/aplicaciones_integral_289.gif]](HTMLFiles/aplicaciones_integral_289.gif)
Supongamos que queremos calcular el área de la región del plano Ω={(ρ cos θ,ρ sen θ): 0≤ρ≤f(θ), α≤θ≤β}. Se trata de la región limitada por la gráfica de la curva dada en coordenadas polares por la ecuación ρ=f(θ), donde f:[α,β]→R es una función continua, y las rectas cuya ecuación en coordendas polares son θ=α, θ=β. Fíjate en la figura.
In[121]:=
![]()
![[Graphics:HTMLFiles/aplicaciones_integral_291.gif]](HTMLFiles/aplicaciones_integral_291.gif)
Lo que hacemos para calcular el área es aproximar Ω por medio de sectores circulares. Recuerda que el área de un sector circular de radio ρ y amplitud φ (medida en radianes) es igual a ![]()
![]() φ. Consideramos para ello una partición α=
φ. Consideramos para ello una partición α=![]() <
<![]() <
<![]() < ... <
< ... <![]() <
<![]() =β de [α,β] y formamos la suma
=β de [α,β] y formamos la suma ![]()
![]()
![]() (
(![]() -
-![]() ). Como el número
). Como el número ![]()
![]() (
(![]() -
-![]() ) es el área del sector circular, representado en azul en la figura, de radio f(
) es el área del sector circular, representado en azul en la figura, de radio f(![]() ) y amplitud igual a
) y amplitud igual a ![]() -
-![]() , es claro que la suma anterior representa una aproximación del área de Ω. Como
, es claro que la suma anterior representa una aproximación del área de Ω. Como ![]()
![]()
![]() (
(![]() -
-![]() ) es una suma de Riemann de la función θ →
) es una suma de Riemann de la función θ → ![]()
![]() , se sigue que el área de Ω viene dada por
, se sigue que el área de Ω viene dada por
![]()
A este mismo resultadose llega teniendo en cuenta que el área de Ω viene dada por
![]()
Con frecuencia, las ecuaciones en coordenadas polares se usan para representar distintos tipos de curvas simétricas llamadas rosas. Por ejemplo, aquí tienes una rosa de 8 hojas o lazos.
In[122]:=
![]()
![[Graphics:HTMLFiles/aplicaciones_integral_321.gif]](HTMLFiles/aplicaciones_integral_321.gif)
La lemniscata es un tipo de rosa de 2 lazos. Fíjate que las rosas no son curvas simples. Para calcular el área de la región del plano encerrada por una rosa, es sufieciente, por simetría, calcular el área encerrada por un lazo y multiplicar por el número de lazos.
Ejemplos
● El área de la región del plano rodeada por un lazo de la lemniscata ![]() = cos(2θ) (-π/4≤t≤π/4) es igual a
= cos(2θ) (-π/4≤t≤π/4) es igual a
![]()
Ejercicios
6 Calcular el área limitada por el arco de la espiral de Arquímides ρ=a θ (a>0) comprendido entre θ=0 y θ=π.
7 Hallar el área encerrada por el lazo interior de la curva ρ= 1/2 +cos θ.
8 Hallar el área encerrada por una de las hojas de la rosa ρ=2 cos(2θ).
9 Calcular el área del lóbulo del folium de Descartes de ecuación ![]() +
+![]() -3 a x y=0, (a>0). Sugerencia: expresar la ecuación en coordenadas polares.
-3 a x y=0, (a>0). Sugerencia: expresar la ecuación en coordenadas polares.
10 Calcular el área de la región común a las dos elipses ![]() +
+![]() =1,
=1,![]() +
+![]() =1. Sugerencia: Representar gráficamente las elipses. Usar la simetría polar para simplificar los cálculos y pasar a coordenadas polares.
=1. Sugerencia: Representar gráficamente las elipses. Usar la simetría polar para simplificar los cálculos y pasar a coordenadas polares.
Longitud de un arco de curva
Se trata de calcular la longitud de la curva γ dada por la ecuación y=f(x), donde suponemos que f:[a,b]→ R es una función con derivada primera continua. Para ello aproximamos la curva por poligonales inscritas en ella. Cada partición a=![]() <
<![]() <
<![]() < ... <
< ... <![]() <
<![]() =b de [a,b] induce una poligonal cuyos vértices son los puntos (
=b de [a,b] induce una poligonal cuyos vértices son los puntos (![]() ,f(
,f(![]() )), 0≤k≤ n. El comando "arclength[{x[t],y[t]},{t,a,b},n]" (código original de Xah Lee) representa la gráfica de la curva cuyas ecuaciones paramétricas son {
)), 0≤k≤ n. El comando "arclength[{x[t],y[t]},{t,a,b},n]" (código original de Xah Lee) representa la gráfica de la curva cuyas ecuaciones paramétricas son {
e inscribe en ella una polígonal de n lados que la divide en n partes que tienen la misma longitud. También calcula la longitud de la poligonal que es una aproximación a la longitud de la curva.
x=x(t)
y=y(t)
In[123]:=
![]()
![[Graphics:HTMLFiles/aplicaciones_integral_338.gif]](HTMLFiles/aplicaciones_integral_338.gif)
In[124]:=
![]()
![[Graphics:HTMLFiles/aplicaciones_integral_340.gif]](HTMLFiles/aplicaciones_integral_340.gif)
In[125]:=
![]()
![[Graphics:HTMLFiles/aplicaciones_integral_342.gif]](HTMLFiles/aplicaciones_integral_342.gif)
In[126]:=
![arclength[{Cos[t]/(Sin[t]^2 + 1), (Sin[t] Cos[t])/(Sin[t]^2 + 1)}, {t, 0, 2π}, 12, AspectRatio→Automatic, ImageSize→ {417, 147.375}] ; (* la lemniscata *)](HTMLFiles/aplicaciones_integral_343.gif)
![[Graphics:HTMLFiles/aplicaciones_integral_344.gif]](HTMLFiles/aplicaciones_integral_344.gif)
In[127]:=
![]()
![[Graphics:HTMLFiles/aplicaciones_integral_346.gif]](HTMLFiles/aplicaciones_integral_346.gif)
La longitud de la poligonal de vértices (![]() ,f(
,f(![]() )), 0≤k≤ n, es igual a
)), 0≤k≤ n, es igual a ![]()
![]() . Por el teorema del valor medio, se verifica que f(
. Por el teorema del valor medio, se verifica que f(![]() )-f(
)-f(![]() )=f '(
)=f '(![]() )(
)(![]() -
-![]() ) para algún
) para algún ![]() ε [
ε [![]() ,
,![]() ]. Por tanto
]. Por tanto![]()
![]() =
=![]()
![]() =
=![]()
![]() (
(![]() -
-![]() )
)
pero esta es una suma de Riemann de la función x→ 1+![]() . Deducimos que la longitud de γ viene dada por
. Deducimos que la longitud de γ viene dada por
![]()
Para el caso de que la curva γ venga dada por las ecuaciones paramétricas {
, (a≤ t≤ b) donde suponemos que las funciones t→x(t), t→ y(t)tienen derivada primera continua, razonando igual que antes se obtiene que la longitud de γ es igual a
x=x(t)
y=y(t)
![]()
Si la curva γ viene dada en coordenadas polares por la ecuación ρ=f(θ), donde f:[α,β]→R es una función con derivada primera continua, entonces la longitud de γ es igual a
![]()
Fórmula que puede deducirse de la anterior sin más que tener en cuenta que las ecuaciones parámetricas de la curva en cuestión son {
, (α≤ θ≤ β).
x=f(θ) cos θ
y=f(θ) sen θ
Ejemplos
● La longitud del arco de la cateneria y=cosh x, entre x=0 y x=1 es igual a
![]()
● La longitud de un arco de la cicloide x=t- sen t, y= 1-cos t es igual a
![]()
Ejercicios
11 Calcular la longitud del arco de curva y=![]() +4, entre x=0 y x=3.
+4, entre x=0 y x=3.
12 Calcular la longitud de la astroide ![]() +
+ ![]() =1, (a>0). Sugerencia: obtener las ecuaciones paramétricas de la astroide y tener en cuenta la simetría.
=1, (a>0). Sugerencia: obtener las ecuaciones paramétricas de la astroide y tener en cuenta la simetría.
13 Calcular la longitud de la cardioide ρ=3(1+cos θ), (0≤θ≤2π).
14 Calcular la longitud de la curva y=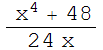 donde 2≤x≤4.
donde 2≤x≤4.
15 Calcular la longitud de la curva y=log(1-![]() ) donde 1/3≤x≤2/3.
) donde 1/3≤x≤2/3.
Volúmenes de sólidos en ![]()
Al igual que podemos calcular áreas de regiones planas integrando las longitudes de sus secciones por rectas paralelas a una dada, podemos también calcular volúmenes de regiones en ![]() integrando las áreas de sus secciones por planos paralelos a uno dado. Este resultado es un caso particular del teorema de Fubini.
integrando las áreas de sus secciones por planos paralelos a uno dado. Este resultado es un caso particular del teorema de Fubini.
Cálculo de volúmenes por secciones planas. El volumen de una región en ![]() es igual a la integral del área de sus secciones por planos paralelos a uno dado.
es igual a la integral del área de sus secciones por planos paralelos a uno dado.
Para justificar esta afirmación, sea Ω una región en ![]() como la de la figura.
como la de la figura.
In[128]:=
![]()
![[Graphics:HTMLFiles/aplicaciones_integral_383.gif]](HTMLFiles/aplicaciones_integral_383.gif)
Representemos por Ω(x) la sección de Ω por el plano perpendicular al eje OX en el punto (x,0,0). Sea V(x) el volumen de la parte de Ω que queda a la izquierda de dicho plano y sea λ(Ω(x)) el área de la sección Ω(x). Observa que la situación es totalmente análoga a la considerada en el Teorema Fundamental del Cálculo: allí teníamos la función área cuya derivada era la longitud de la sección. No debe sorprenderte por ello que ahora resulte que la derivada de la función volumen, V(x), sea el área de la sección. En efecto, sea h>0. Suponiendo, naturalmente, que la función x→λ(Ω(x)) es continua, tenemos que
![]()
de donde se deduce que
![]()
Análogamente se procede si h<0. Hemos obtenido así que V'(x)=λ(Ω(x)). Deducimos que el volumen de Ω viene dado por
![]()
Podemos llegar también a este resultado considerando sumas de Riemann. Para ello aproximamos la región Ω por cilindros de la siguiente forma. Consideremos una partición a=![]() <
<![]() <
<![]() < ... <
< ... <![]() <
<![]() =b de [a,b]; la parte de Ω comprendida entre los planos perpendiculares al eje OX por los puntos (
=b de [a,b]; la parte de Ω comprendida entre los planos perpendiculares al eje OX por los puntos (![]() ,0,0) y (
,0,0) y (![]() ,0,0) puede aproximarse por un cilindro de altura
,0,0) puede aproximarse por un cilindro de altura ![]() -
-![]() y base Ω(
y base Ω(![]() ) cuyo volumen es igual a λ(Ω(
) cuyo volumen es igual a λ(Ω(![]() ))(
))(![]() -
-![]() ). Observa la figura (ten paciencia, tarda un poco).
). Observa la figura (ten paciencia, tarda un poco).
In[129]:=

![]()
![[Graphics:HTMLFiles/aplicaciones_integral_402.gif]](HTMLFiles/aplicaciones_integral_402.gif)
La suma de los volúmenes de todos estos cilindros, ![]() λ(Ω(
λ(Ω(![]() ))(
))(![]() -
-![]() ) es por tanto una aproximación del volumen de Ω, pero dicha suma es una suma de Riemann de la función x→λ(Ω(x)) (a≤x≤b), por lo que el volumen de Ω es igual a Vol(Ω)=
) es por tanto una aproximación del volumen de Ω, pero dicha suma es una suma de Riemann de la función x→λ(Ω(x)) (a≤x≤b), por lo que el volumen de Ω es igual a Vol(Ω)=![]() λ(Ω(x))dx.
λ(Ω(x))dx.
Vamos a estudiar algunos casos en los que es fácil calcular el área de las secciones de Ω.
Volumen de un cuerpo de revolución
Los cuerpos de revolución o sólidos de revolución son regiones de ![]() que se obtienen girando una región plana alrededor de una recta llamada eje de giro. La orden "SurfaceOfRevolution[f[x],{x,a,b},opts]" representa la superficie de revolución obtenida girando la gráfica de f en el plano YZ. Este comando tiene muchas opciones, búscalas en la ayuda de Mathematica. Aquí tienes el sólido de revolución engendrado al girar alrededor del eje OX la gráfica de la función seno entre 0 y π.
que se obtienen girando una región plana alrededor de una recta llamada eje de giro. La orden "SurfaceOfRevolution[f[x],{x,a,b},opts]" representa la superficie de revolución obtenida girando la gráfica de f en el plano YZ. Este comando tiene muchas opciones, búscalas en la ayuda de Mathematica. Aquí tienes el sólido de revolución engendrado al girar alrededor del eje OX la gráfica de la función seno entre 0 y π.
In[131]:=

![[Graphics:HTMLFiles/aplicaciones_integral_410.gif]](HTMLFiles/aplicaciones_integral_410.gif)
Método de los discos: secciones perpendiculares al eje de giro
Sea f:[a,b]→R una función continua. Girando la región del plano comprendida entre la curva y= f(x), el eje de abscisas y las rectas y=a e y=b, alrededor del eje OX obtenemos un sólido de revolución Ω. Es evidente que la sección, Ω(x), de Ω por el plano perpendicular al eje OX en el punto (x,0,0), (a≤x≤b), es un disco contenido en dicho plano de centro (x,0,0) y radio |f(x)|. Por tanto el área de Ω(x) es λ(Ω(x))=π ![]() ; en consecuencia el volumen de Ω es igual a
; en consecuencia el volumen de Ω es igual a
![]()
El volumen del sólido de revolución, Ω, obtenido girando alrededor del eje OX una región de tipo I definida por dos funciones continuas f,g:[a,b]→R tales que 0≤f(x)≤g(x) para todo x ε [a,b], viene dado por
![]()
Una expresión similar se obtiene para el volumen de un sólido de revolución obtenido girando alrededor del eje OY una región de tipo II.
Ejemplos
● El volumen de la esfera obtenida girando la circunferencia ![]() +
+![]() =
=![]() alrededor del eje OX es igual a π
alrededor del eje OX es igual a π![]() (
(![]() -
-![]() )dx=
)dx=![]() .
.
● Un cono circular recto de altura h y radio de la base R se obtiene girando la recta y=R x/h entre 0 y h. Su volumen es igual a π ![]()
![]() dx=
dx=![]() π
π ![]() h.
h.
Ejercicios
16 Calcular el volumen del sólido engendrado al girar alrededor del eje OX la parte de la curva y= ![]() x comprendida entre x=0 y x=π.
x comprendida entre x=0 y x=π.
17 Calcular el volumen del sólido engendrado al girar alrededor del eje OX la gráfica de la función f:[0,+∞[→R dada por f(x)=![]() .
.
18 Calcular el volumen del sólido engendrado al girar la región limitada por la parábola ![]() =4x y la recta x =4 alrededor de dicha recta.
=4x y la recta x =4 alrededor de dicha recta.
19 Calcular el volumen del sólido engendrado al girar la región limitada por las parábolas ![]() =x,
=x, ![]() =y alrededor del eje OX.
=y alrededor del eje OX.
20 Calcular el volumen del elipsoide ![]() +
+![]() +
+![]() =1.
=1.
21 Calcular el volumen limitado por el paraboloide ![]() +
+![]() =z y el plano z=7.
=z y el plano z=7.
Método de las láminas o de los tubos
Consideremos la gráfica de una función positiva y=f(x) a≤x≤b. Por ejemplo
In[132]:=
![]()
![[Graphics:HTMLFiles/aplicaciones_integral_436.gif]](HTMLFiles/aplicaciones_integral_436.gif)
Giremos dicha gráfica alrededor del eje OY.
In[133]:=
![]()
![[Graphics:HTMLFiles/aplicaciones_integral_438.gif]](HTMLFiles/aplicaciones_integral_438.gif)
Obtenemos así un sólido de revolución, Ω, cuyo volumen podemos aproximar considerando rectángulos verticales inscritos en la gráfica y girándolos alrededor del eje OY.
In[134]:=

![[Graphics:HTMLFiles/aplicaciones_integral_440.gif]](HTMLFiles/aplicaciones_integral_440.gif)
Ejecuta la siguiente celda para ver cómo la aproximación va mejorando a medidad que aumentamos el número de puntos de división del intervalo.

![[Graphics:HTMLFiles/aplicaciones_integral_448.gif]](revolucion.gif)
Esto es lo que se conoce como método de las láminas o de los tubos. Observa que, a diferencia del método de los discos en el que se consideran rectángulos perpendiculares al eje de giro, en el método de las láminas o de los tubos los rectángulos considerados son paralelos al eje de giro.
Consideremos una partición a=![]() <
<![]() <
<![]() < ... <
< ... <![]() <
<![]() =b de [a,b]. El volumen del sólido engendrado al girar alrededor del eje OY un rectángulo vertical cuya base es el intervalo [
=b de [a,b]. El volumen del sólido engendrado al girar alrededor del eje OY un rectángulo vertical cuya base es el intervalo [![]() ,
,![]() ] y altura f(
] y altura f(![]() ) es igual a π (
) es igual a π (![]() -
-![]() )f(
)f(![]() )=π(
)=π(![]() +
+![]() )f(
)f(![]() )(
)(![]() -
-![]() ). La suma de todos ellos es igual a
). La suma de todos ellos es igual a
![]()
Como las sumas ![]() π
π ![]() f(
f(![]() )(
)(![]() -
-![]() ) y
) y ![]() π
π ![]() f(
f(![]() )(
)(![]() -
-![]() ) son sumas de Riemann de la función x→ π x f(x), deducimos que el volumen de Ω viene dado por
) son sumas de Riemann de la función x→ π x f(x), deducimos que el volumen de Ω viene dado por
![]()
Puedes adaptar fácilmente esta expresión para el caso de que el eje de giro sea la recta vertical x=c. En general, si notamos por R(x) el radio de giro de la lámina, entonces
![]()
Ejemplos
● Consideremos el toro T obtenido al girar el disco de centro (a,0) , a>0, y radio R alrededor del eje OY. Puedes verlo para a=2 y R=1 ejecutando la siguiente celda.
In[139]:=
![[Graphics:HTMLFiles/aplicaciones_integral_479.gif]](HTMLFiles/aplicaciones_integral_479.gif)
Por simetría, su volumen es el doble del volumen del sólido obtenido al girar la semicircunferencia y=![]() , (a-R≤x≤a+R) alrededor del eje OY. Por tanto
, (a-R≤x≤a+R) alrededor del eje OY. Por tanto
![]()
● Calcular el volumen del sólido Ω engendrado al girar la región limitada por las parábolas ![]() =x,
=x, ![]() =y alrededor del eje OY.
=y alrededor del eje OY.
In[140]:=
![]()
![[Graphics:HTMLFiles/aplicaciones_integral_485.gif]](HTMLFiles/aplicaciones_integral_485.gif)
In[141]:=

![[Graphics:HTMLFiles/aplicaciones_integral_487.gif]](HTMLFiles/aplicaciones_integral_487.gif)
El sólido de revolución engendrado es una especie de embudo acotado por dos superficies de revolución, la superior obtenida al girar la gráfica y=![]() y la inferior obtenida al girar y=
y la inferior obtenida al girar y=![]() . El volumen pedido viene, por tanto, dado por Vol(Ω)=2π
. El volumen pedido viene, por tanto, dado por Vol(Ω)=2π![]() (x
(x![]() -
-![]() )dx=
)dx=![]() .
.
Ejercicios
22 Calcular el volumen del toro engendrado al girar el círculo de centro 0 y radio 3 alrededor de la recta x=6.
23 Calcular el volumen del sólido Ω engendrado al girar la región limitada por las parábolas ![]() =x,
=x, ![]() =y alrededor de la recta x=4.
=y alrededor de la recta x=4.
Área de una superficie de revolución
Una superficie de revolución se obtiene girando una curva dada alrededor de una recta. Sea f:[a,b]→R una función con derivada primera continua. Girando la gráfica de dicha función alrededor del eje OX obtenemos una superficie de revolución, Γ. Fíjate en la siguiente representación.
In[142]:=
![]()
![[Graphics:HTMLFiles/aplicaciones_integral_497.gif]](HTMLFiles/aplicaciones_integral_497.gif)
Sea S(x) el área de la parte de la superficie comprendida entre los planos X=a, y X=x. Representemos por L(x) la longitud de la gráfica de f entre a y x. Recuerda que L(x)=![]()
![]() dt. Teniendo en cuenta que el área lateral de un cilindro circular recto es igual a la longitud de la base por la altura, se deduce que
dt. Teniendo en cuenta que el área lateral de un cilindro circular recto es igual a la longitud de la base por la altura, se deduce que
2π min{f(t):x≤t≤x+h}(L(x+h)-L(x))≤S(x+h)-S(x)≤2π max{f(t):x≤t≤x+h}(L(x+h)-L(x))
Por tanto
![]()
Tomando límites para h→0 deducimos que S'(x)=2π f(x) L'(x)=2π f(x)![]() . Luego el área de la superficie Γ viene dada por
. Luego el área de la superficie Γ viene dada por
![]()
Ejemplos
● El área de una superficie esférica de radio R viene dada por 2π![]()
![]()
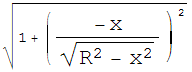 dx=4 π
dx=4 π ![]() .
.
Ejercicios
24 Calcular el área de la superficie de revolución engendrada al girar la curva y=![]() , 0≤x≤1, alrededor del eje OX.
, 0≤x≤1, alrededor del eje OX.
25 Calcular el área de la superficie de revolución engendrada al girar la curva ![]() +
+![]() =
=![]() , (a>0), alrededor del eje OX.
, (a>0), alrededor del eje OX.
26 Calcular el área de la superficie de revolución engendrada al girar la elipse ![]() +
+![]() =1 alrededor del eje OY.
=1 alrededor del eje OY.
27 Calcular el área de la superficie de revolución engendrada al girar la catenaria y=cosh x, 0≤x≤1, alrededor del eje OX.
28 Al girar alrededor del eje OX el segmento de parábola y=![]() , 0≤x≤a, engendra un tronco de paraboloide de revolución cuya superficie tiene área igual a la de una esfera de radio
, 0≤x≤a, engendra un tronco de paraboloide de revolución cuya superficie tiene área igual a la de una esfera de radio ![]() . Se pide calcular el valor de a.
. Se pide calcular el valor de a.
29 Comprueba que el área de la superficie de revolución (llamada horno de Gabriel) engendrada al girar la curva y=1/x, 1≤x<+∞, alrededor del eje OX es infinita (por tanto sería necesaria una cantidad infinita de pintura si quisiéramos pintarla) pero el volumen del sólido de revolución engendrado es finito (por tanto podemos llenarlo con una cantidad finita de pintura). Comenta a tu gusto esta aparente paradoja.
30 Calcular el área de un espejo parabólico de 3 metros de diámetro y 1 metro de fondo.
| Created by Mathematica (September 20, 2008) |