Contraste de hipótesis. Un contraste de hipótesis es un proceso estadístico mediante el cual se investiga si una propiedad que se supone que cumple una población es compatible con lo observado en una muestra de dicha población. Es un procedimiento que permite elegir una hipótesis de trabajo de entre dos posibles y antagónicas.
Hipótesis Estadística. Todo contraste de hipótesis se basa en la formulación de dos hipótesis exhaustivas y mutuamente exclusivas:
La hipótesis H0 es la que se desea contrastar. Consiste generalmente en una afirmación concreta sobre la forma de una distribución de probabilidad o sobre el valor de alguno de los parámetros de esa distribución. El nombre de "nula" significa “sin valor, efecto o consecuencia”, lo cual sugiere que H0 debe identificarse con la hipótesis de no cambio (a partir de la opinión actual); no diferencia, no mejora, etc. H0 representa la hipótesis que mantendremos a no ser que los datos indiquen su falsedad, y puede entenderse, por tanto, en el sentido de “neutra”. La hipótesis H0 nunca se considera probada, aunque puede ser rechazada por los datos. Por ejemplo, la hipótesis de que dos poblaciones tienen la misma media puede ser rechazada fácilmente cuando ambas difieren mucho, analizando muestras suficientemente grandes de ambas poblaciones, pero no puede ser "demostrada" mediante muestreo, puesto que siempre cabe la posibilidad de que las medias difieran en una cantidad lo suficientemente pequeña para que no pueda ser detectada, aunque la muestra sea muy grande. Dado que descartaremos o no la hipótesis nula a partir de muestras obtenidas (es decir, no dispondremos de información completa sobre la población), no será posible garantizar que la decisión tomada sea la correcta.
La hipótesis H1 es la negación de la nula. Incluye todo lo que H0 excluye.
¿Qué asignamos como H0 y H1 ?
La hipótesis H0 asigna un valor específico al parámetro en cuestión y por lo tanto “el igual” siempre forma parte de H0.
La idea básica de la prueba de hipótesis es que los hechos tengan probabilidad de rechazar H0. La hipótesis H0 es la afirmación que podría ser rechazada por los hechos. El interés del investigador se centra, por lo tanto, en la H1.
La regla de decisión. Es el criterio que vamos a utilizar para decidir si la hipótesis nula planteada debe o no ser rechazada. Este criterio se basa en la partición de la distribución muestral del estadístico de contraste en dos regiones o zonas mutuamente excluyentes: Región crítica o región de rechazo y Región de no-rechazo.
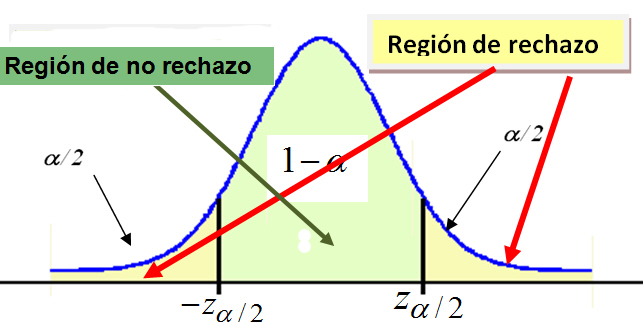
Región de no-rechazo. Es el área de la distribución muestral que corresponde a los valores del estadístico de contraste próximos a la afirmación establecida en H0. Es decir, los valores del estadístico de contraste que nos conducen a decidir H0. Es por tanto, el área correspondiente a los valores del estadístico de contraste que es probable que ocurran si H0 es verdadera. Su probabilidad se denomina nivel de confianza y se representa por 1 - α .
Región de rechazo o región crítica. Es el área de distribución muestral que corresponde a los valores del estadístico de contraste que se encuentran tan alejados de la afirmación establecida en H0, que es muy poco probable que ocurran si H0 es verdadera. Su probabilidad se denomina nivel de significación o nivel de riesgo y se representa con la letra α .
Ya definidas las dos zonas, la regla de decisión consiste en rechazar H0 si el estadístico de contraste toma un valor perteneciente a la zona de rechazo, o mantener H0 si el estadístico de contraste toma un valor perteneciente a la zona de no-rechazo.
El tamaño de las zonas de rechazo y no-rechazo se determina fijando el valor de α, es decir, fijando el nivel de significación con el que se desea trabajar. Se suele tomar un 1% o un 5%.
La forma de dividir la distribución muestral en zona de rechazo y de no-rechazo depende de si el contraste es bilateral o unilateral. La zona crítica debe situarse donde puedan aparecer los valores muestrales incompatibles con H0.
Estadístico de contraste. Un estadístico de contraste es un resultado muestral que cumple la doble condición de:
Tipos de contrastes.
Contrastes paramétricos: Conocida una v.a. con una determinada distribución, se establecen afirmaciones sobre los parámetros de dicha distribución.
Contrastes no paramétricos: Las afirmaciones establecidas no se hacen en base a la distribución de las observaciones, que a priori es desconocida .
Tipos de hipótesis del contraste.
Hipótesis simples: La hipótesis asigna un único valor al parámetro desconocido, H: θ = θ0
Hipótesis compuestas: La hipótesis asigna varios valores posibles al pará metro desconocido, H: θ ∈ ( θ1 , θ2 )
H0 = θ = θ0 H1 = θ ≠ θ0 |
|
H0 = θ ≤ θ0 H1 =θ > θ0 |
|
H0 = θ ≥ θ0 H1 = θ < θ0 |
|
La Reglas de decisión.
Se rechaza H0 si el estadístico de contraste cae en la zona crítica, es decir, si el estadístico de contraste toma un valor tan grande o tan pequeño que la probabilidad de obtener un valor tan extremo o más que el encontrado es menor que α /2.

Se rechaza H0 si el estadístico de contraste cae en la zona crítica, es decir, si toma un valor tan grande que la probabilidad de obtener un valor como ese o mayor es menor que α .
Contraste bilateral
H0 = θ = θ0 H1 = θ ≠ θ0 |
Contraste unilateral: Cola a la derecha
H0 = θ ≤ θ0 H1 =θ > θ0 |
Contraste unilateral: Cola a la izquierda
H0 = θ ≥ θ0 H1 = θ < θ0 |
La decisión:
Planteada la hipótesis, formulados los supuestos, definido el estadístico de contraste y su distribución muestral, y establecida la regla de decisión, el paso siguiente es obtener una muestra aleatoria de tamaño n, calcular el estadístico de contraste y tomar una decisión:
Si rechazamos Ho afirmamos que la hipótesis es falsa, es decir, que afirmamos con una probabilidad α de equivocarnos, que hemos conseguido probar que esa hipótesis es falsa. Por el contrario, si no la rechazamos, no estamos afirmando que la hipótesis sea verdadera. Simplemente que no tenemos evidencia empírica suficiente para rechazarla y que se considera compatible con los datos.
Como conclusión, si se mantiene o no se rechaza H0, nunca se puede afirmar que es verdadera.
Errores de Tipo I y II.
P[ Rechazar H0 / H0 es verdadera ] = α
P[ No rechazar H0 / H0 es falsa ] = β
Por tanto,
El siguiente cuadro resume las ideas:
Verdadera
Decisión Rechazar H0 Error de tipo I
P = α
Decisión correcta
P = 1 - β
No rechazar H0 Decisión correcta
P = 1 - α
Error de tipo II
P = β

Relaciones entre los errores de Tipo I y II. El estudio de las relaciones entre los errores lo realizamos mediante el contraste de hipótesis:
![]()
Para ello utilizamos la información muestral proporcionada por el estadístico media muestral ![]()
Cuanto más se aleje el valor μ1 de μ0 , más hacia la derecha se desplazará la curva H1 , y en consecuencia, más pequeña se hará el área β . Por lo tanto, el valor de β depende del valor concreto de μ1 que consideremos verdadero dentro de todos los afirmados por H1 .
En lugar de buscar procedimientos libres de error, debemos buscar procedimientos para los que no sea probable que ocurran ningún tipo de estos errores. Esto es, un buen procedimiento es aquel para el que es pequeña la probabilidad de cometer cualquier tipo de error. La elección de un valor particular de corte de la región de rechazo fija las probabilidades de errores tipo I y tipo II.
Debido a que H0 especifica un valor único del parámetro, hay un solo valor de α . Sin embargo, hay un valor diferente de β por cada valor del parámetro recogido en H1 .
En general, un buen contraste o buena regla de decisión debe tender a minimizar los dos tipos de error inherentes a toda decisión. Como α queda fijado por el investigador, trataremos de elegir una región donde la probabilidad de cometer el error de tipo II sea la menor .
Usualmente, se diseñan los contrastes de tal manera que la probabilidad a sea el 5% (0,05), aunque a veces se usan el 10% (0,1) o 1% (0,01) para adoptar condiciones más relajadas o más estrictas.
Potencia de un contraste. Es la probabilidad de decidir H1 cuando ésta es cierta
P[ decidir H1 / H1 es verdadera ] = 1 - β
El concepto de potencia se utiliza para medir la bondad de un contraste de hipótesis. Cuanto más lejana se encuentra la hipótesis H1 de H0 menor es la probabilidad de incurrir en un error tipo II y, por consiguiente, la potencia tomará valores más próximos a 1.
Si la potencia en un contraste es siempre muy próxima a 1 entonces se dice que el estadístico de contraste es muy potente para contrastar H0 ya que en ese caso las muestras serán, con alta probabilidad, incompatibles con H0 cuando H1 sea cierta.
Por tanto puede interpretarse la potencia de un contraste como su sensibilidad o capacidad para detectar una hipótesis alternativa. La potencia de un contraste cuantifica la capacidad del criterio utilizado para rechazar H0 cuando esta hipótesis sea falsa
Es deseable en un contraste de hipótesis que las probabilidades de ambos tipos de error fueran tan pequeñas como fuera posible. Sin embargo, con una muestra de tamaño prefijado, disminuir la probabilidad del error de tipo I, α, conduce a incrementar la probabilidad del error de tipo II, β. El recurso para aumentar la potencia del contraste, esto es, disminuir la probabilidad de error de tipo II, es aumentar el tamaño muestral lo que en la práctica conlleva un incremento de los costes del estudio que se quiere realizar
El concepto de potencia nos permite valorar cual entre dos contrastes con la misma probabilidad de error de tipo I, α, es preferible. Se trata de escoger entre todos los contrastes posibles con α prefijado aquel que tiene mayor potencia, esto es, menor probabilidad β de incurrir en el error de tipo II. En este caso el Lema de Neyman-Pearson garantiza la existencia de un contraste de máxima potencia y determina cómo construirlo.
Potencia de un contraste de hipótesis
El propósito de los contrastes de hipótesis es determinar si un valor propuesto (hipotético) para un parámetro u otra característica de la población debe aceptarse como plausible con base en la evidencia muestral.
Podemos considerar las siguientes etapas en la realización de un contraste:
Los contrastes de hipótesis que construye SPSS son los proporcionados por las Pruebas T, estas son de tres tipos: Prueba T para una muestra, Prueba T para muestras independientes y Prueba T para muestras relacionadas
El procedimiento Prueba T para una muestra mediante SPSS contrasta si la media de una población difiere de una constante especificada. Para obtener una Prueba T para una muestra se elige, en el menú principal, Analizar/Comparar medias/Prueba T para una muestra...
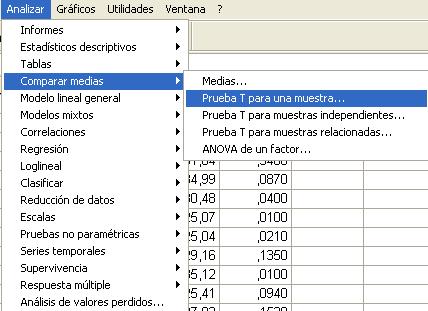
En la salida correspondiente se selecciona una o más variables cuantitativas para contrastarlas con el mismo valor supuesto.
Por ejemplo, en la siguiente salida se muestra un contraste para el caso en que la media de la variable longitud sea igual a 20 (Valor de prueba: 20)

Pulsando Opciones... se puede elegir el nivel de confianza.

Se pulsa Continuar y Aceptar. Se obtiene un resumen estadístico para la muestra y la salida del procedimiento.

Esta salida muestra el tamaño muestral, la media, la desviación típica y error típico de la media.

Esta salida muestra los resultados del contraste de la t de Student con un intervalo de confianza para la diferencia entre el valor observado y el valor teórico (contrastado). Cada una de las columnas de la tabla muestra:
De un modo general, dos muestras se dice que son independientes cuando las observaciones de una de ellas no condicionan para nada a las observaciones de la otra, siendo dependientes en caso contrario. En realidad, el tipo de dependencia que se considera a estos efectos es muy especial: cada dato de una muestra tiene un homónimo en la otra, con el que está relacionada, de ahí el nombre alternativo de muestras apareadas. Por ejemplo, supongamos que se quiere estudiar el efecto de un medicamento, sobre la hipertensión, a un grupo de 20 individuos. El experimento se podría planificar de dos formas:
El paquete estadístico SPSS realiza el procedimiento Prueba T para muestras independientes; en este procedimiento se compara la media de dos poblaciones normales e independientes. Para realizar dicho contraste los sujetos deben asignarse aleatoriamente a las dos poblaciones, de forma que cualquier diferencia en la respuesta sea debida al tratamiento (o falta de tratamiento) y no a otros factores.
El procedimiento Prueba T para muestras independientes mediante SPSS contrasta si la diferencia de las medias de dos poblaciones normales e independientes difiere de una constante especificada. Para obtener una Prueba T para muestras independiente se selecciona, en el menú principal, Analizar/Comparar medias/Prueba T para muestras independientes...

Se accede a la siguiente ventana

donde se puede seleccionar una o más variables cuantitativas y se calcula una Prueba T diferente para cada variable. Por ejemplo, en esta salida se selecciona la variable asimetría.
A continuación se selecciona una sola variable de agrupación, en nuestro caso, la variable Parte y se pulsa Definir Grupos para especificar los códigos de los grupos que se quieran comparar. Vamos a contrastar la igualdad de medias de la variable asimetría según la variable Parte (Canopy, Sprouts)

Pulsando Definir Grupos... se muestra la siguiente pantalla

donde se especifican el número de grupos que se quieren comparar.
Se pulsa Continuar y después Aceptar y se obtienen las siguientes pantallas que muestran un resumen estadístico para las dos muestras y la salida del procedimiento.


Para realizar un contraste de diferencia de medias de dos poblaciones independientes hay que contrastar previamente las varianzas de dichas poblaciones. Esta salida nos muestra el valor experimental del estadístico de contraste (Fexp = 2.045), este valor deja a la derecha un área igual a 0.176 (Sig.= 0.176), por lo tanto no se puede rechazar la hipótesis nula de igualdad de varianzas.
A continuación se realiza el contraste para la diferencia de medias suponiendo que las varianzas son iguales. La tabla nos muestra el valor experimental del estadístico de contraste (texp = 1.233) y el p-valor = 0.240 (Sig.= 0.240), por lo tanto no se puede rechazar la hipótesis nula de igualdad de medias. También, se puede concluir el contraste observando que el intervalo de confianza para la diferencia de medias (-0.05256, 0.192264) contiene al cero.
El paquete estadístico SPSS realiza el procedimiento Prueba T para muestras apareadas; en este procedimiento se comparan las medias de dos variables de un solo grupo. Calcula las diferencias entre los valores de cada caso y contrasta si la media difiere de cero.
Para obtener una Prueba T para muestras relacionadas se elige en los menús Analizar/Comparar medias/Prueba T para muestras relacionadas...

Se accede a la siguiente ventana

donde se selecciona un par de variables pulsando en cada una de ellas. La primera variable aparecerá en la sección Selecciones actuales como Variable 1 y la segunda aparecerá como Variable 2. Una vez seleccionado el par de variables, en nuestro caso Asim95 y Asim97, se pulsa el botón de flecha para moverlas a la ventana de Variables relacionadas. Se puede realizar el contraste para más de una pareja de variables simultáneamente.

Al pulsar Continuar y después Aceptar se obtiene un resumen estadístico para las dos muestras y la salida del procedimiento.

Para cada variable se presenta la media, tamaño de la muestra, desviación típica y error típico de la media.

Esta salida muestra para cada pareja de variables: el número de datos, el coeficiente de correlación y el p-valor asociado al contraste H0: r = 0 frente a H1: r <> 0. El coeficiente de correlación es igual a -0.681, por lo tanto las variables están relacionadas en sentido inverso, cuando una crece la otra decrece. Observando el p-valor (0.206) deducimos que no se puede rechazar la hipótesis nula (H0: r = 0) por lo tanto no existe correlación entre las variables. (La correlación no es significativa).

Esta salida muestra el valor experimental del estadístico de contraste (t = 3.908) y el p-valor igual a 0.017, por lo tanto se debe rechazar la hipótesis nula de igualdad de medias.
El contraste de hipótesis para la comparación de dos proporciones independientes se basa en la distribución aproximada de un estadístico muestral que requiere muestras grandes. El paquete estadístico SPSS no incluye el cálculo de dicho estadístico pero permite el cálculo de otros cuatro estadísticos para muestras grandes y el estadístico exacto de Fisher para muestras pequeñas.
El contraste de comparación de dos proporciones es un caso particular del contraste de homogeneidad de dos muestras de una variable cualitativa cuando ésta sólo presenta dos modalidades. Por ello, el procedimiento que vamos a realizar es el análisis de una tabla de contingencia 2x2.
Para obtener el procedimiento Tablas de contingencia se elige en los menús Analizar/Estadísticos descriptivos/Tablas de contingencia...
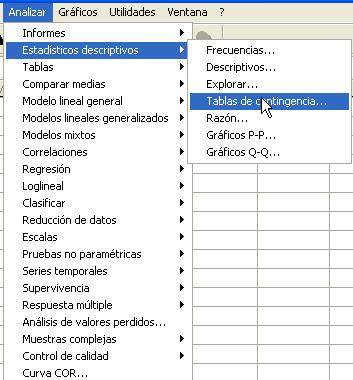
En la ventana emergente se seleccionan las variables dicotómicas que se van a contrastar. Por ejemplo, en la siguiente salida se muestra el procedimiento de Tablas de contingencia en el que se comparan las variables Sexo y Fumador, para ello se han seleccionado la variable Sexo y mediante el botón de flecha se ha pasado al campo Filas: y la variable Fumador que se ha pasado al campo Columnas: (Se desea comparar la proporción de fumadores en los grupos (hombres y mujeres)).

Se pulsa el botón Casillas... y se selecciona en Frecuencias (Observadas) y en Porcentajes (Fila)

Se pulsa Continuar y en la pantalla correspondiente se pulsa el botón Estadísticos... y se selecciona Chi-cuadrado
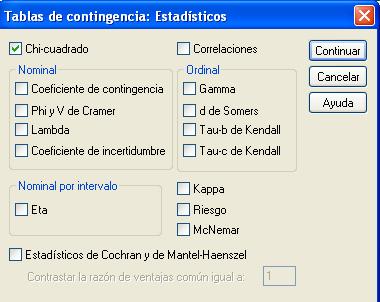
Se pulsa Continuar y Aceptar. Se muestran la Tabla de contingencia y los contrastes Chi-cuadrado

Cada casilla de esta tabla muestra la frecuencia observada y el porcentaje que ésta representa sobre el total de la fila la tabla de contingencia Sexo * Fumador. Las proporciones muestrales que vamos a comparar son 10/26 y 14/24 . Para ello se realiza un contraste bilateral para evaluar si existen diferencias significativas entre ambas proporciones muestrales (H0: p1 - p2=0 frente a H1: p1 - p2 <>0)

Esta tabla muestra los resultados de cinco estadísticos para la comparación de ambas proporciones. Generalmente, en el caso de muestras grandes se elige el estadístico Corrección por continuidad. Dicho estadístico calcula el estadístico Chi-cuadrado con la corrección por continuidad de Yates. En nuestro caso, el valor de dicho estadístico es 1.259 y el p-valor asociado es 0.262 (Sig. asintótica bilateral) por lo tanto no se debe rechazar la Hipótesis nula, es decir las diferencias observadas entre las proporciones de fumadores en los dos grupos no son estadísticamente significativas.
En el caso de muestras pequeñas, se decide a partir del Estadístico exacto de Fisher.
En la sesión anterior hemos estudiado contrastes de hipótesis acerca de parámetros poblacionales, tales como la media y la varianza, de ahí el nombre de contrastes paramétricos. En estadística paramétrica se trabaja bajo el supuesto de que las poblaciones poseen distribuciones conocidas, donde cada función de distribución teórica depende de uno o más parámetros poblacionales. Sin embargo, en muchas situaciones, es imposible especificar la forma de la distribución poblacional. El proceso de obtener conclusiones directamente de las observaciones muestrales, sin formar los supuestos con respecto a la forma matemática de la distribución poblacional se llama teoría no paramétrica. En esta sesión vamos a realizar procedimientos que no exigen ningún supuesto, o muy pocos acerca de la familia de distribuciones a la que pertenece la población, y cuyas observaciones pueden ser cualitativas o bien se refieren a alguna característica ordenable. Estos procedimientos reciben el nombre de Contrastes de hipótesis no paramétricos.
Así, uno de los objetivos de esta sesión es el estudio de contrates de hipótesis para determinar si una población tiene una distribución teórica específica. La técnica que nos introduce a estudiar esas cuestiones se llama Contraste de la Chi-cuadrado para la Bondad de Ajuste. Una variación de este contraste se emplea para resolver los Contrastes de Independencia. Tales contrastes pueden utilizarse para determinar si dos características (por ejemplo preferencia política e ingresos) están relacionadas o son independientes. Y, por último estudiaremos otra variación del contraste de la bondad de ajuste llamado Contraste de Homogeneidad. Tal contraste se utiliza para estudiar si diferentes poblaciones, son similares (u homogéneas) con respecto a alguna característica. Por ejemplo, queremos saber si las proporciones de votantes que favorecen al candidato A, al candidato B o los que se abstuvieron son las mismas en dos ciudades.
Hemos agrupado los procedimientos en los que el denominador común a todos ellos es que su tratamiento estadístico se aborda mediante la distribución Chi-cuadrado. El procedimiento Prueba de Chi-cuadrado tabula una variable en categorías y calcula un estadístico de Chi-cuadrado. Esta prueba compara las frecuencias observadas y esperadas en cada categoría para contrastar si todas las categorías contienen la misma proporción de valores o si cada categoría contiene una proporción de valores especificada por el usuario.
Para obtener una prueba de Chi-cuadrado se eligen en los menús Analizar/Pruebas no paramétricas/Cuadros de diáologo antiguos/Chi-cuadrado...
En la salida correspondiente se selecciona una o más variables de contraste. Cada variable genera una prueba independiente.
Por ejemplo, en la siguiente salida se muestra una Prueba de Chi-cuadrado en la que la variable a contrastar es Día de la semana (Se desea saber si el número de altas diarias de un hospital difiere dependiendo del día de la semana)

Se pulsa Opciones... para obtener estadísticos descriptivos, cuartiles y controlar el tratamiento de los datos perdidos

Al pulsar Continuar y Aceptar se muestran las siguientes salidas

En esta salida se muestra:
N observado: Muestra la frecuencia observada para cada fila (día). Se observa, en esta tabla, que el número de altas diarias de un total de 589 altas por semana es: 44 el domingo, 78 el lunes etc.
N esperado: Muestra el valor esperado para cada fila (suma de las frecuencias observadas dividida por el número de filas). En este ejemplo hay 589 altas observadas por semana, resultando alrededor de 84 altas por día.
Residual: Muestra el residuo (frecuencia observada menos el valor esperado). La tabla muestra que el domingo hay muchas menos altas de pacientes que el viernes. De lo que parece deducirse que todos los días de la semana no tienen la misma proporción de altas de pacientes.
Por último la siguiente salida muestra el resultado del contraste Chi-cuadrado

El valor experimental del estadístico de contraste de Chi-cuadrado es igual a 29.389 y el p-valor asociado es menor que 0.001 (Sig = 0.000), por lo tanto se rechaza la hipótesis nula. En consecuencia, el número de altas en los pacientes difiere dependiendo del día de la semana.
El procedimiento Tablas de contingencia proporciona una serie de pruebas y medidas de asociación para tablas de doble clasificación.
Para obtener tablas de contingencia se selecciona, en el menú principal, Analizar/Estadísticos descriptivos/Tablas de contingencia...

En el cuadro de diálogo resultante se especifican las variables que forman la tabla. Una de las variables se introduce en Filas: y la otra variable se introduce en Columnas:

En este cuadro de diálogo se pulsa el botón Estadísticos... y se accede a otra ventana donde se especifican los valores numéricos que se desea obtener. Se selecciona Chi-cuadrado

Se pulsa Continuar y se selecciona Casillas... para obtener frecuencias observadas y esperadas, porcentajes y residuos

Se pulsa Continuar y se selecciona Formato para especificar el orden de las categorías (ascendente o descendente)

Se pulsa Continuar y Aceptar. Se muestran las siguientes salidas

donde:
La siguiente salida nos muestra la Tabla de Contingencia de las variables seleccionadas

Por último muestra el resultado del contraste de hipótesis.

El p-valor (Sig = 0.256) indica que no debe rechazarse la hipótesis de independencia.
El procedimiento Prueba binomial compara las frecuencias
observadas de las dos categorías de una variable dicotómica con las frecuencias
esperadas en una distribución binomial con un parámetro de probabilidad especificado.
Por defecto, el parámetro de probabilidad para ambos grupos es 0.5. Se puede
cambiar el parámetro de probabilidad en el primer grupo. Siendo la probabilidad
en el segundo grupo igual a uno menos la probabilidad del primer grupo.
Si las variables no son dicotómicas se debe especificar un punto de corte. Mediante
el punto de corte se divide la variable en dos grupos, el formado por los casos
mayores o iguales que el punto de corte y el formado por los casos menores que
el punto de corte.
Para obtener una Prueba binomial se selecciona, en el menú principal, Analizar/Pruebas no paramétricas/Binomial...

En la salida correspondiente se selecciona una o más variables de contraste numéricas.

Se deja la opción por defecto Contrastar proporción: 0.50. (Queremos ver si el porcentaje de mujeres en un determinado estudio es del 50%, es decir, queremos contrastar H0: p = 0.5 frente a H1: p <> 0.5). En esta ventana se pulsa el botón Opciones... y se accede a otra ventana para obtener estadísticos descriptivos, cuartiles y controlar el tratamiento de los datos perdidos.
Se pulsa Aceptar y se muestra la siguiente salida

SPSS realiza un contraste bilateral. De un total de 474 personas se observa que el 54 % son hombres y el 46% son mujeres. El p-valor del contraste (Sig. asintót. bilateral) es 0.06, nos indica que no debe rechazarse la hipótesis nula.
Este procedimiento permite dicotomizar una variable continua. Por ejemplo, queremos saber si el 30% de las personas de un estudio son menores de 25 años. Para resolverlo, en el campo Definir la dicotomía pondríamos en el Punto de corte: el valor de 25 y en el campo Contrastar proporción: pondríamos 0.30.
El procedimiento Prueba de Rachas contrasta si es aleatorio el orden de aparición de los valores de una variable. Se puede utilizar para determinar si la muestra fue extraída de manera aleatoria.
Una racha es una secuencia de observaciones similares, una sucesión de símbolos idénticos consecutivos. Ejemplo: + + - - - + - - + + + + - - - (6 rachas). Una muestra con un número excesivamente grande o excesivamente pequeño de rachas sugiere que la muestra no es aleatoria.
Para obtener una Prueba de Rachas se selecciona, en el menú principal, Analizar/Pruebas no paramétricas/Cuadros de diáologo antiguos/Rachas...
En la salida correspondiente se selecciona una o más variables de contraste numéricas.

En el campo Punto de corte se especifica un punto de corte para dicotomizar las variables seleccionadas. Se puede utilizar como punto de corte los valores observados para la media, la mediana o la moda, o bien un valor especificado. Los casos con valores menores que el punto de corte se asignarán a un grupo y los casos con valores mayores o iguales que el punto de corte se asignarán a otro grupo. Se lleva a cabo una prueba para cada punto de corte seleccionado. En esta ventana se pulsa el botón Opciones... y se accede a otra ventana para obtener estadísticos descriptivos, cuartiles y controlar el tratamiento de los datos perdidos.
Se pulsa Aceptar y se obtiene la salida del procedimiento

En esta salida se muestran los siguientes valores:
El procedimiento Prueba de Kolmogorov-Smirnov para una muestra compara la función de distribución acumulada observada de una variable con una distribución teórica determinada, que puede ser la distribución Normal, la Uniforme, la de Poisson o la Exponencial. La Z de Kolmogorov-Smirnov se calcula a partir de la diferencia mayor (en valor absoluto) entre las funciones de distribución acumulada teórica y observada. Esta prueba de bondad de ajuste contrasta si las observaciones podrían razonablemente proceder de la distribución especificada.
Para obtener una Prueba de Kolmogorov-Smirnov se selecciona, en el menú principal, Analizar/Pruebas no paramétricas/Cuadros de diálogo antiguos/K-S de 1 muestra...
Se muestra la siguiente ventana

En esta salida se puede elegir una o más variables de contraste numéricas, cada variable genera una prueba independiente. Elegiremos la variable Crecimiento, una vez seleccionada la variable se pasa al campo Contrastar variable: mediante el botón de flecha o pulsando dos veces en la variable

Se selecciona la distribución a la que queremos ajustar los datos en el campo Distribución de contraste. En esta ventana se pulsa el botón Opciones... y se accede a otra ventana para obtener estadísticos descriptivos, cuartiles y controlar el tratamiento de los datos perdidos
Se pulsa Aceptar y se obtiene la salida del procedimiento

En esta salida se muestran los siguientes valores:
El p-valor (Sig. Asintót (bilateral) = 0.002) indica que debe rechazarse la hipótesis H0 de normalidad, de forma que no se admite que la distribución de los datos sea de tipo Normal.
El procedimiento Pruebas para dos muestras independientes compara dos grupos de casos existentes en una variable y comprueba si provienen de la misma población (homogeneidad). Estos contrastes, son la alternativa no paramétrica de los tests basados en el t de Student, sirven para comparar dos poblaciones independientes. SPSS dispone de cuatro pruebas para realizar este contraste.
La prueba U de Mann-Whitney es la más conocida de la pruebas para dos muestras independientes. Es equivalente a la prueba de la suma de rangos de Wilcoxon y a la prueba de Kruskal-Wallis para dos grupos. Requiere que las dos muestras probadas sean similares en la forma y contrasta si dos poblaciones muestreadas son equivalentes en su posición.
La prueba Z de Kolmogorov-Smirnov y la prueba de rachas de Wald-Wolfowitz son pruebas más generales que detectan las diferencias entre las posiciones y las formas de las distribuciones. La prueba de Kolmogorov-Smirnov se basa en la diferencia máxima absoluta entre las funciones de distribución acumulada observadas para ambas muestras. Cuando esta diferencia es significativamente grande, se consideran diferentes las dos distribuciones. La prueba de rachas de Wald-Wolfowitz combina y ordena las observaciones de ambos grupos. Si las dos muestras proceden de una misma población, los dos grupos deben dispersarse aleatoriamente en la ordenación de los rangos.
La prueba de reacciones extremas de Moses presupone que la variable experimental afectará a algunos sujetos en una dirección y a otros en dirección opuesta. La prueba contrasta las respuestas extremas comparándolas con un grupo control.
Para obtener Pruebas para dos muestras independientes se selecciona, en el menú principal, Analizar/Pruebas no paramétricas/Cuadros de diálogo antiguos/2 muestras independientes...

Se muestra la siguiente ventana

En esta salida se puede elegir una o más variables de contraste numéricas. Se elige la variable Tiempo, una vez seleccionada la variable se pasa al campo Contrastar variable: mediante el botón de flecha o pulsando dos veces en la variable. Se selecciona una variable de agrupación, en nuestro caso la variable es Grupo (Se desea saber si las persona fumadoras tardan más tiempo en dormirse que las no fumadoras)

Se pulsa Definir grupos..., para dividir el archivo en dos grupos o muestras, y emerge la siguiente ventana

Para segmentar el archivo en dos grupos o muestras se introduce un valor entero para el Grupo 1 y un valor entero para el Grupo 2. Así, en los campos Grupo 1 y Grupo 2 se ponen los valores con los que están codificados Fumador (con 1) y NoFumador (con 2), respectivamente. Como indica la siguiente salida

Se pulsa Continuar y como está marcado por defecto el test U de Mann-Whitney se pulsa Aceptar y se obtiene las siguientes salidas

Las observaciones de ambos grupos se combinan para formar una sola muestra, se ordenan linealmente y se les asigna un rango, asignándose el rango promedio en caso de producirse empate, conservando su identidad como grupo. El estadístico W de Wilcoxon (Wm) es la suma de los rangos asociados con las observaciones que originariamente constituyen la muestra menor (Fumadores). Se realiza está elección ya que se piensa que si la población de Fumadores está situada por debajo de la población de NoFumadores, entonces los rangos menores tenderán a asociarse con los valores de los Fumadores. Ello producirá un valor pequeño para el estadístico Wm. Si es cierto lo contrario (la población de Fumadores está situada por encima de la población de NoFumadores) entonces los rangos mayores se encontrarán entre los Fumadores, dando lugar a un valor grande del estadístico Wm. De esta forma, se rechaza H0 si el valor observado Wm fuera demasiado pequeño o demasiado grande para que se debiera al azar.
Si las diferencias entre los grupos se deben al azar, el rango promedio de los dos grupos debería ser aproximadamente igual. En la salida anterior se observa que hay una diferencia de alrededor de siete minutos (Rango promedio de Fumadores es 17.67 el de los NoFumadores es 11.07). Siendo mayor el tiempo que tarda en dormirse los Fumadores.
En la siguiente salida se muestran los valores experimentales de los estadísticos de contrastes y el p-valor asociado

SPSS calcula dos estadísticos: U de Mann-Whitney y W de Wilcoxon, como ambos estadísticos son equivalentes SPSS muestra un único valor de p-valor (Sig). Además, en el cálculo de dicho p-valor aplica una aproximación a la distribución normal, la cual sólo es válida para muestras grandes.
El estadístico U de Mann-Whitney, como el de W de Wilcoxon, dependen de las observaciones de los dos grupos linealmente ordenadas. El estadístico U es el número de veces que un valor de los Fumadores precede al de los NoFumadores. El Estadístico U será grande si la población de los Fumadores está situada por encima de la población de los NoFumadores y será pequeño si sucede lo contario.
El estadístico de contraste Wm es la suma de los rangos asociados a los Fumadores. Como sospechamos que los Fumadores tardan más tiempo en quedarse dormidos que los NoFumadores, se rechaza la Hipótesis nula de que no existen diferencias entre los dos grupos si el valor de Wm es demasiado pequeño para que se deba al azar.
El p-valor asociado al contraste, 0.032, nos conduce a rechazar la hipótesis nula de que no existe diferencias entre los dos grupos y concluimos que los Fumadores tienden a tardar más tiempo en quedarse dormidos que los NoFumadores.
Estas pruebas comparan las distribuciones de dos poblaciones relacionadas. Se supone que la distribución de población de las diferencias emparejadas es simétrica.
SPSS dispone de cuatro pruebas para realizar este contraste, la prueba de signos, la prueba de Wilcoxon de los rangos con signo, la prueba de McNemar y la prueba de homogeneidad marginal. La prueba apropiada depende del tipo de datos:
Para obtener pruebas para dos muestras relacionadas se selecciona, en el menú principal, Analizar/Pruebas no paramétricas/ Cuadros de diálogo antiguos/2 muestras relacionadas...

Se muestra la siguiente ventana

En esta salida se puede elegir una o más variables de contraste numéricas. Para ello, se pulsa en cada una de las variables. La primera de ellas aparecerá en la sección Selecciones actuales como Variable1, se pulsa en la variable Crudo; la segunda variable aparecerá como Variable2, se pulsa en la variable Cocido. A continuación se pulsa en el botón de flecha para incluir las variables en la campo Contrastar pares: Se pulsa Aceptar y se muestra la siguiente salida

En el text de Wilcoxon, los rangos están basados en el valor absoluto de la diferencia entre las dos variables contrastadas. El signo de la diferencia es usado para clasificar los casos en uno o tres grupos: diferencia menor que 0 (rangos negativos), mayor que cero (rangos positivos) o igual a cero (empates). Los casos de empates son ignorados

El p-valor asignado al contraste 0.021 (Sig asintótica bilateral) nos indica que se debe rechazar la hipótesis nula de que no existen diferencias entre los dos grupos.