COVID-19
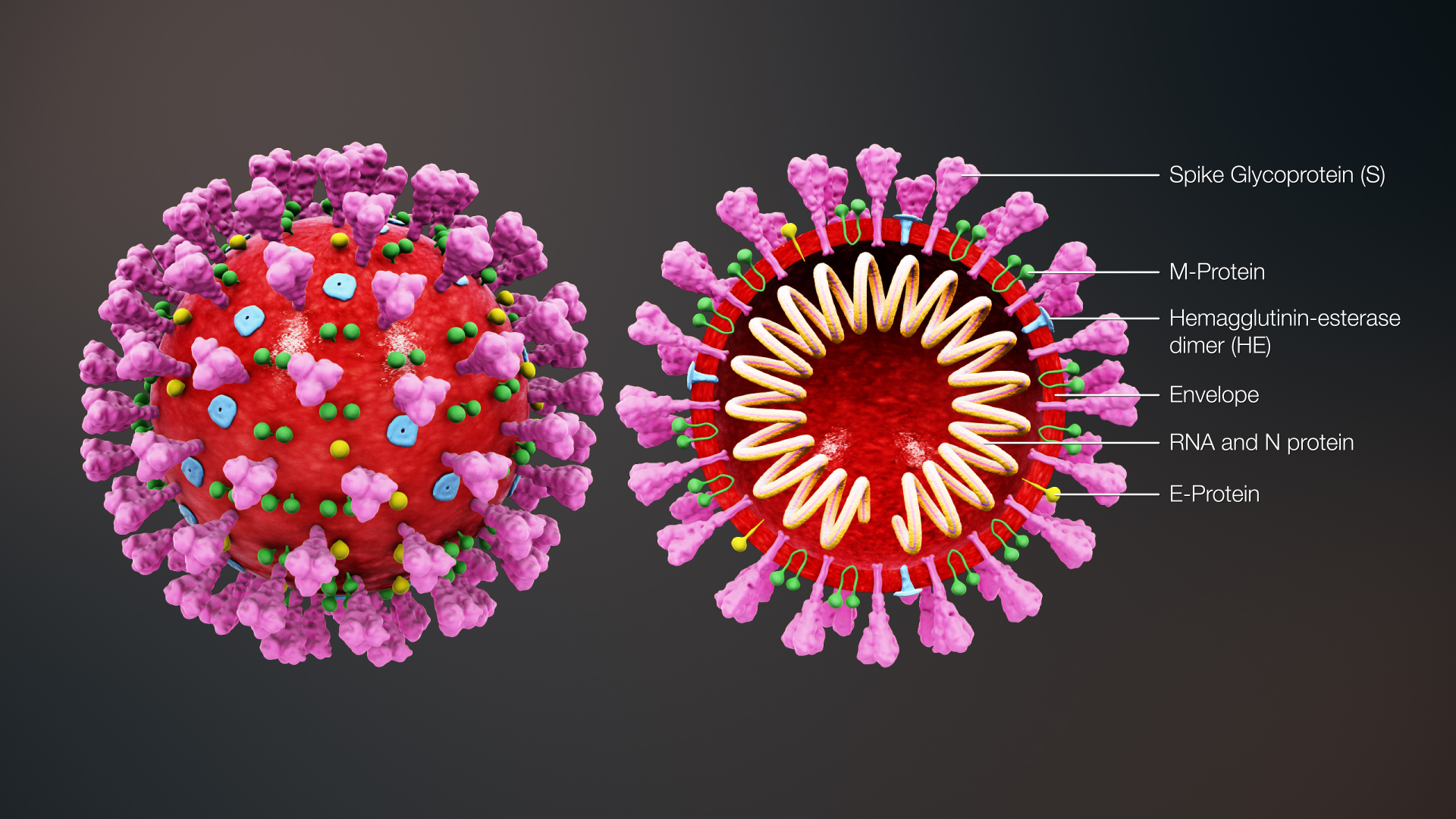
-
NEW VIDEO - SIMULATION OF VIRUS PROPAGATION
SIMULATION CENSURED BY GOOGLE PLAY AND AMAZON APPS
Video made by J.E. Amaro with the Android app Pandemic
Monte Carlo simulation in a lattice. Planck P-model
-
DOWNLOAD PANDEMIC APP FOR ANDROID
Click on the image above to download the PANDEMIC APP for Android
Monte Carlo simulation in a lattice with temperature T, representing the average
movility (or energy) of the individuals
-
DOWLOAD THE ORIGINAL PAPERS ON EPIDEMIC MODELS
1.- The D model for deaths by COVID-19
J.E. Amaro
Preprint (unpublished) -
FITS OF PANDEMIC MODELS AND PREDICTIONS
We provide here our daily fits to the current data.
A basic function to parametrize the total deaths is
D(t) = a exp(t/b) / ( 1 + c exp (t/b) )
The values of the parametes a, b, c are at the top of the plots
Click on the figures to enlarge
WE ALSO PROVIDE PLOTS FOR THE MODELS:
D2, is the sum of two D-functions
D'2, is the derivative of the D2 function to fit the deaths-per-day
Extended SIR model where the recovered function r = R/N
is parametrized similarly as the D-function
Monte Carlo P-model. Virus simulation propagating in a grid of cells
-
SOUTH AFRICA FITS AND PREDICTIONS
Click here for SOUTH AFRICA fits:

-
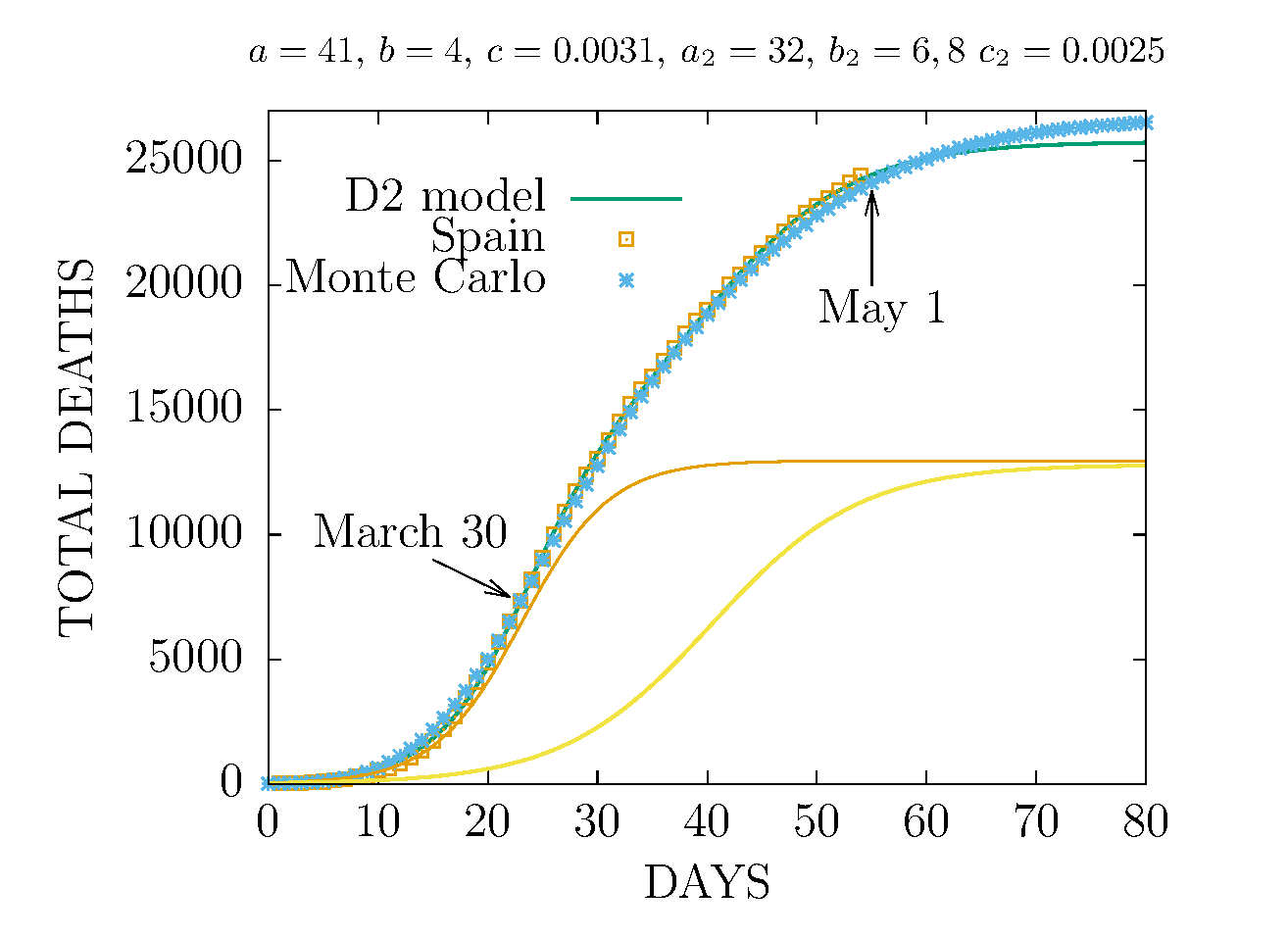
MODEL D2 AND MONTE CARLO - TOTAL DEATHS IN SPAIN 30 MAY
The Monte Carlo was fitted to data up to May 2. After the final data corrections by the Ministry of Health, Spain reached the Monte Carlo predictions for the total deaths at the maximum of the curve.
-
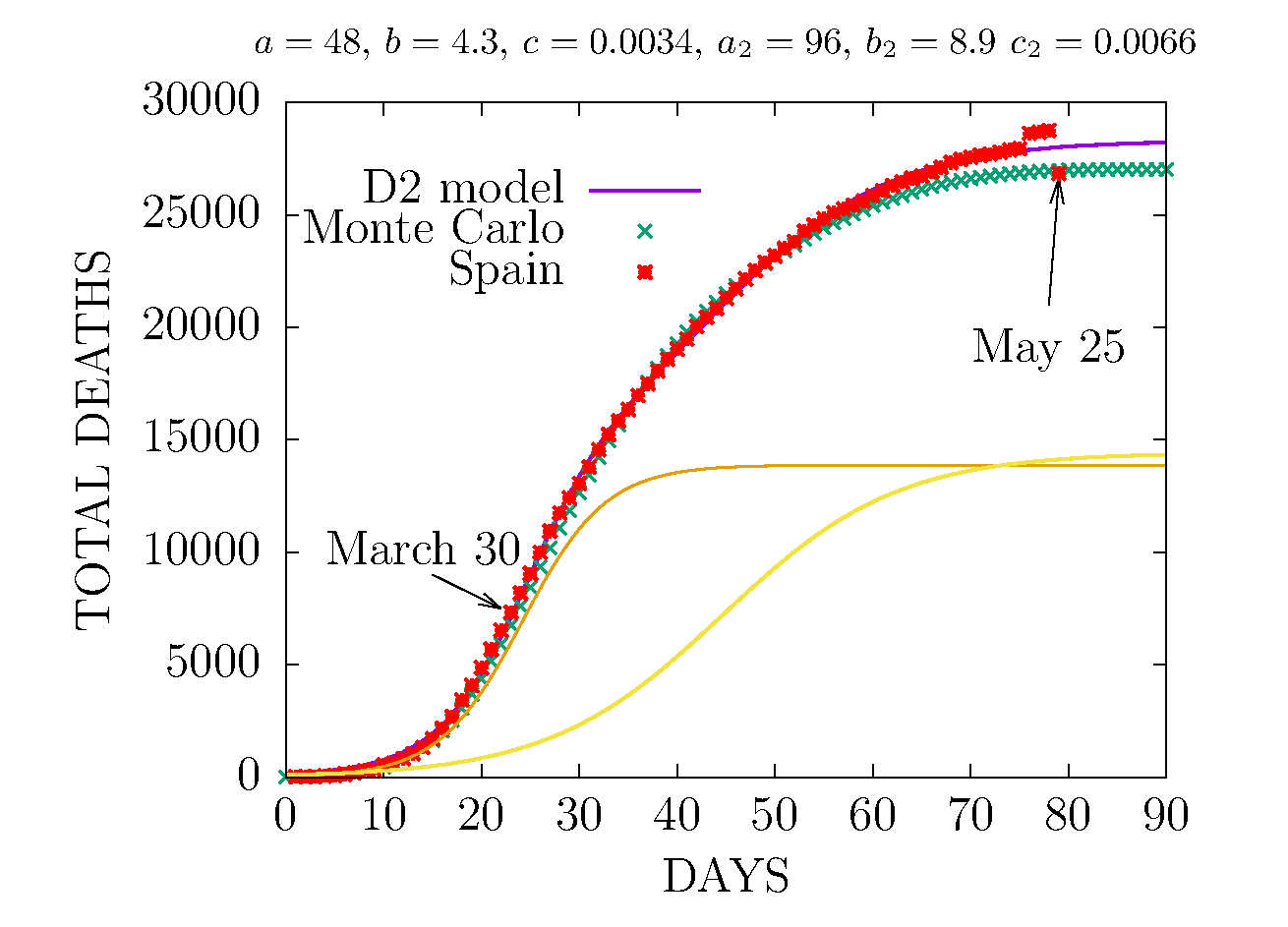
MODEL D2 AND MONTE CARLO - TOTAL DEATHS IN SPAIN 25 MAY
The Monte Carlo was fitted to data up to May 2. After the data correction by the Ministry of Health on May 25, Spain reached the Monte Carlo predictions for the total deaths at the maximum of the curve.
-
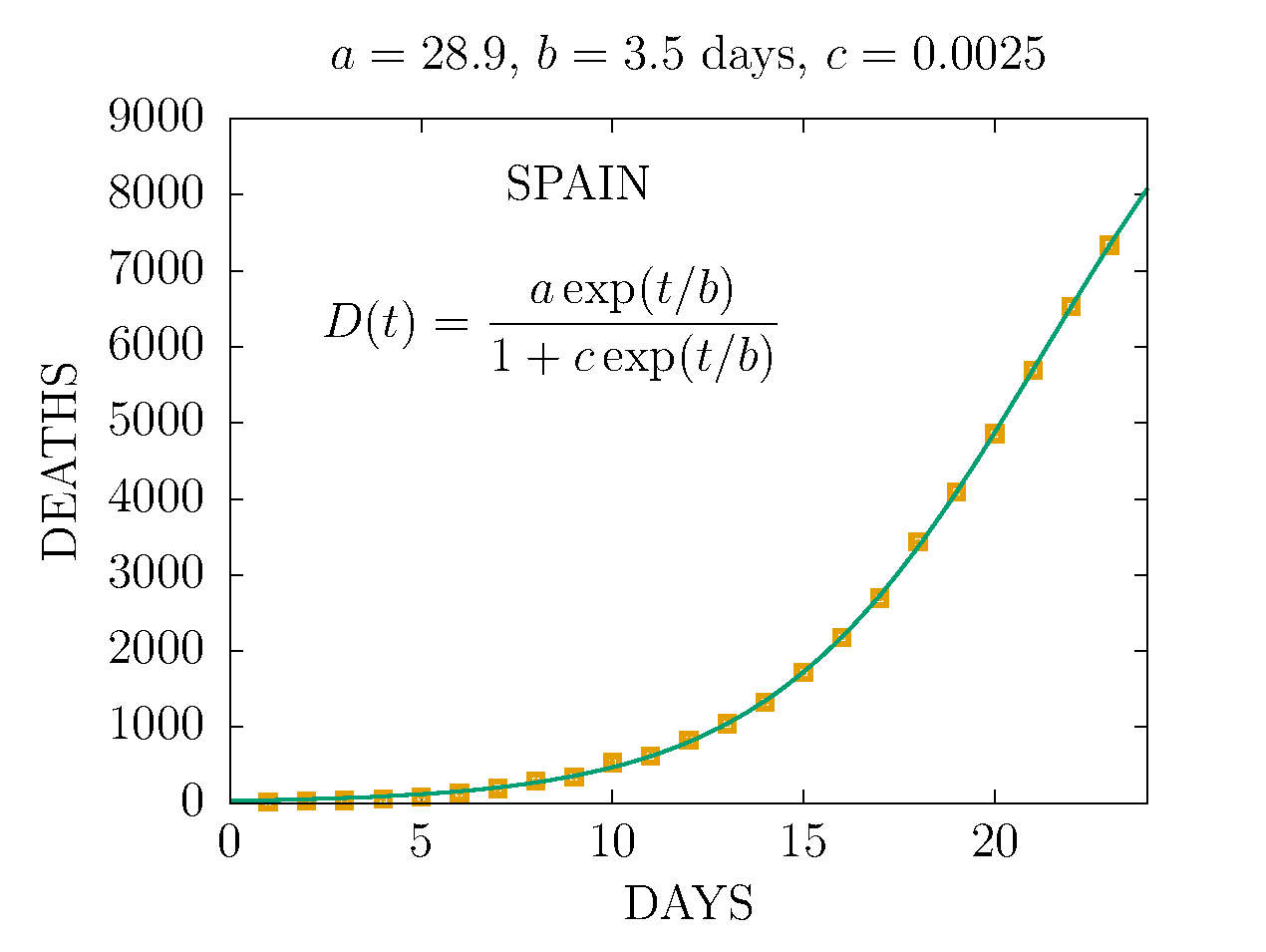
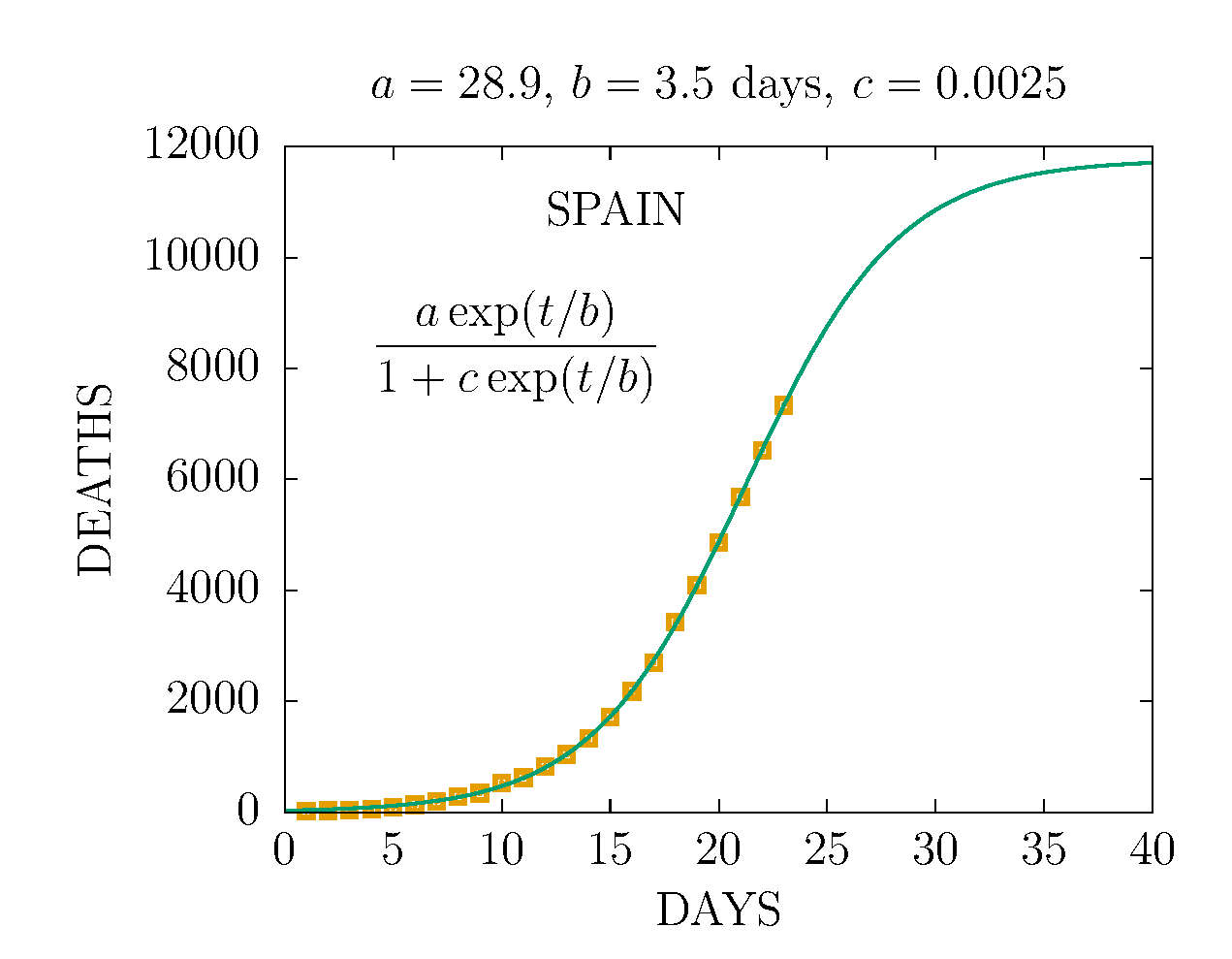
D MODEL - COMPARISON DEATHS IN SPAIN 23 MAY AND 23 MARCH
This fit to deaths in Spain up to 23 March shows the uncertainty of of the D-model with few data is quite large (200% in this case)
-
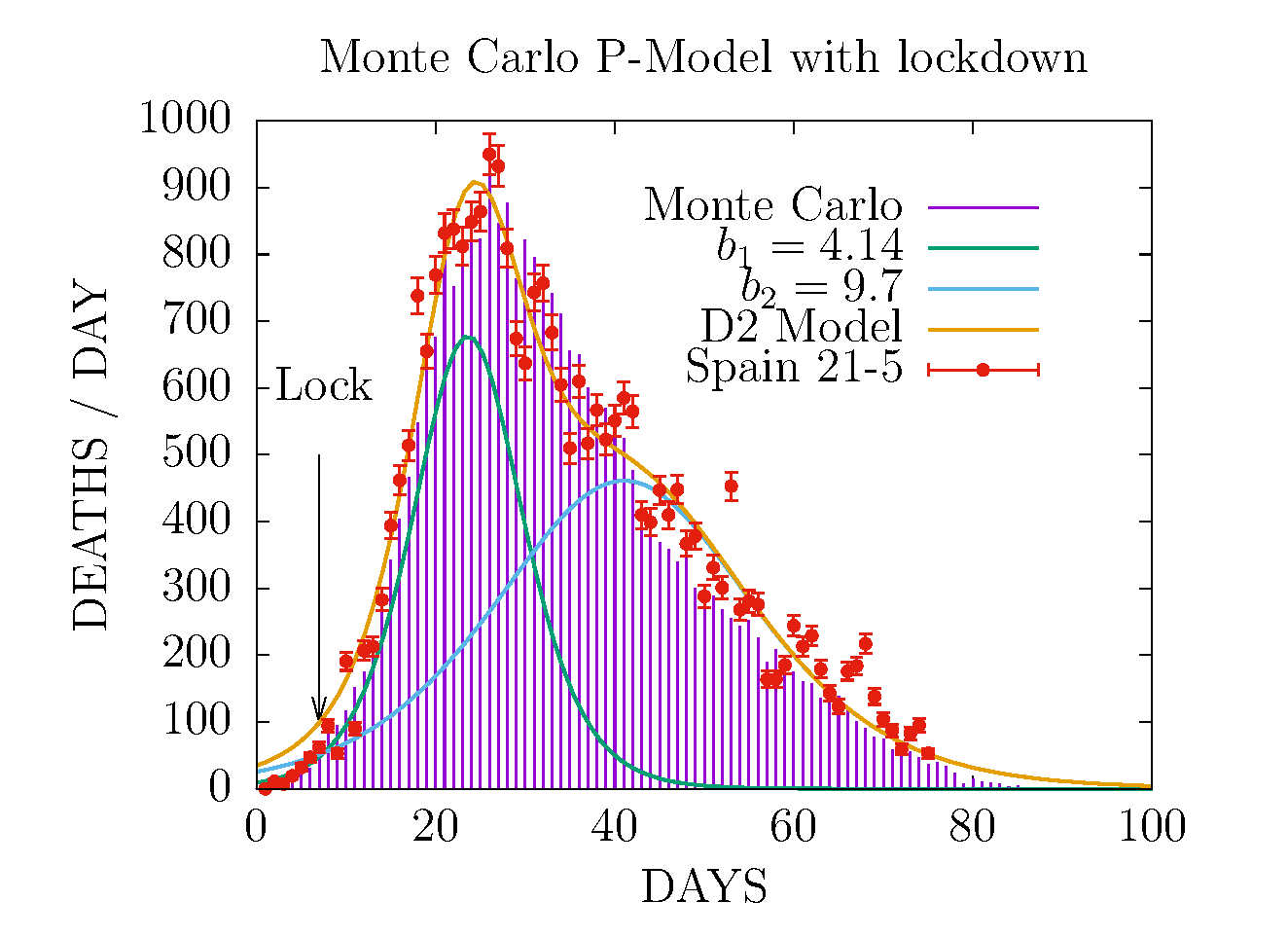
MODEL D2 AND MONTE CARLO - DEATHS-PER-DAY IN SPAIN 21 MAY
This Monte Carlo was fitted to data up to May 2
-
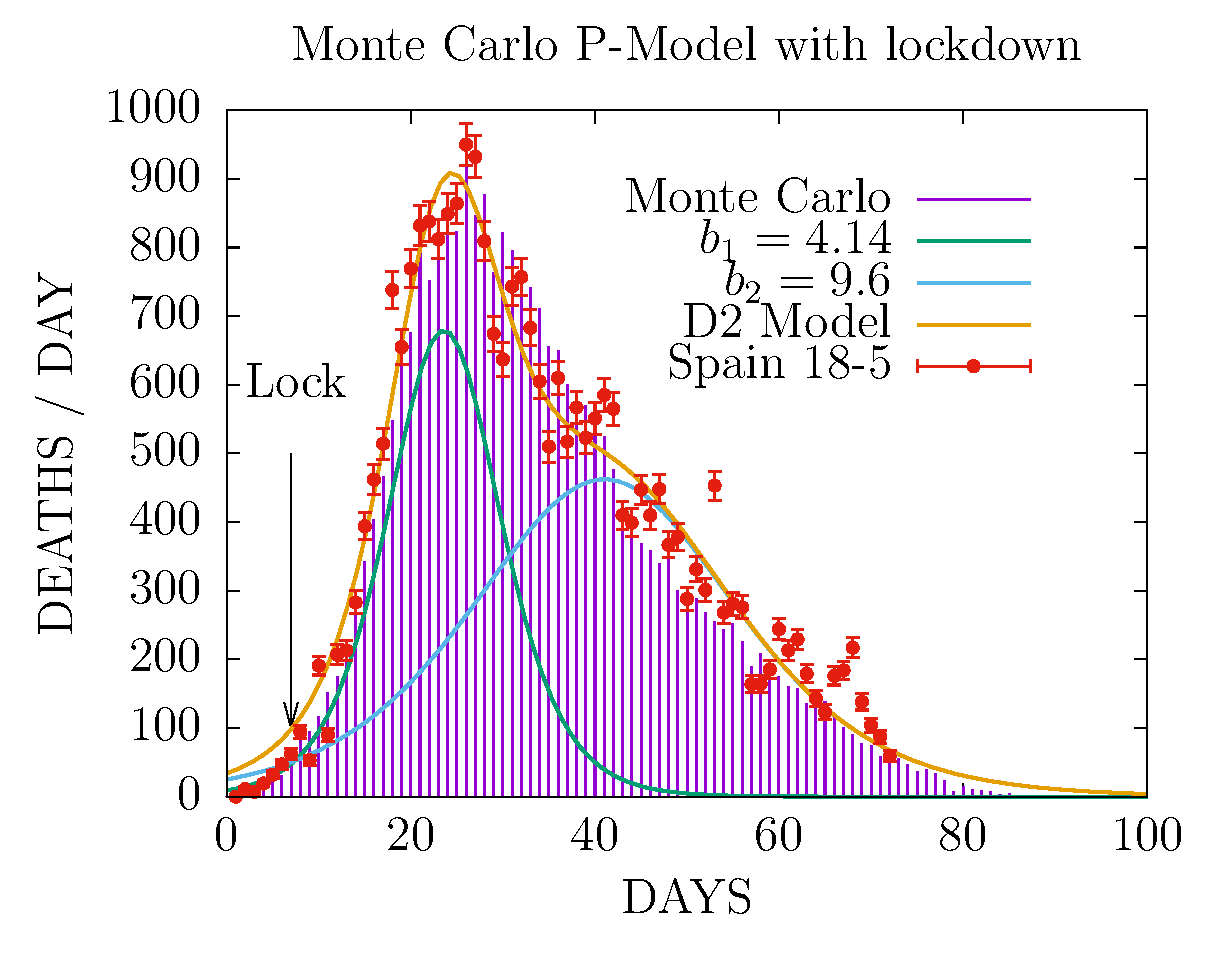
MODEL D2 AND MONTE CARLO - DEATHS-PER-DAY IN SPAIN 18 MAY
This Monte Carlo was fitted to data up to May 2
-
MODEL D2 AND MONTE CARLO - TOTAL DEATHS IN SPAIN 17 MAY
The Monte Carlo was fitted to data up to May 2 and is now subestimating data
-
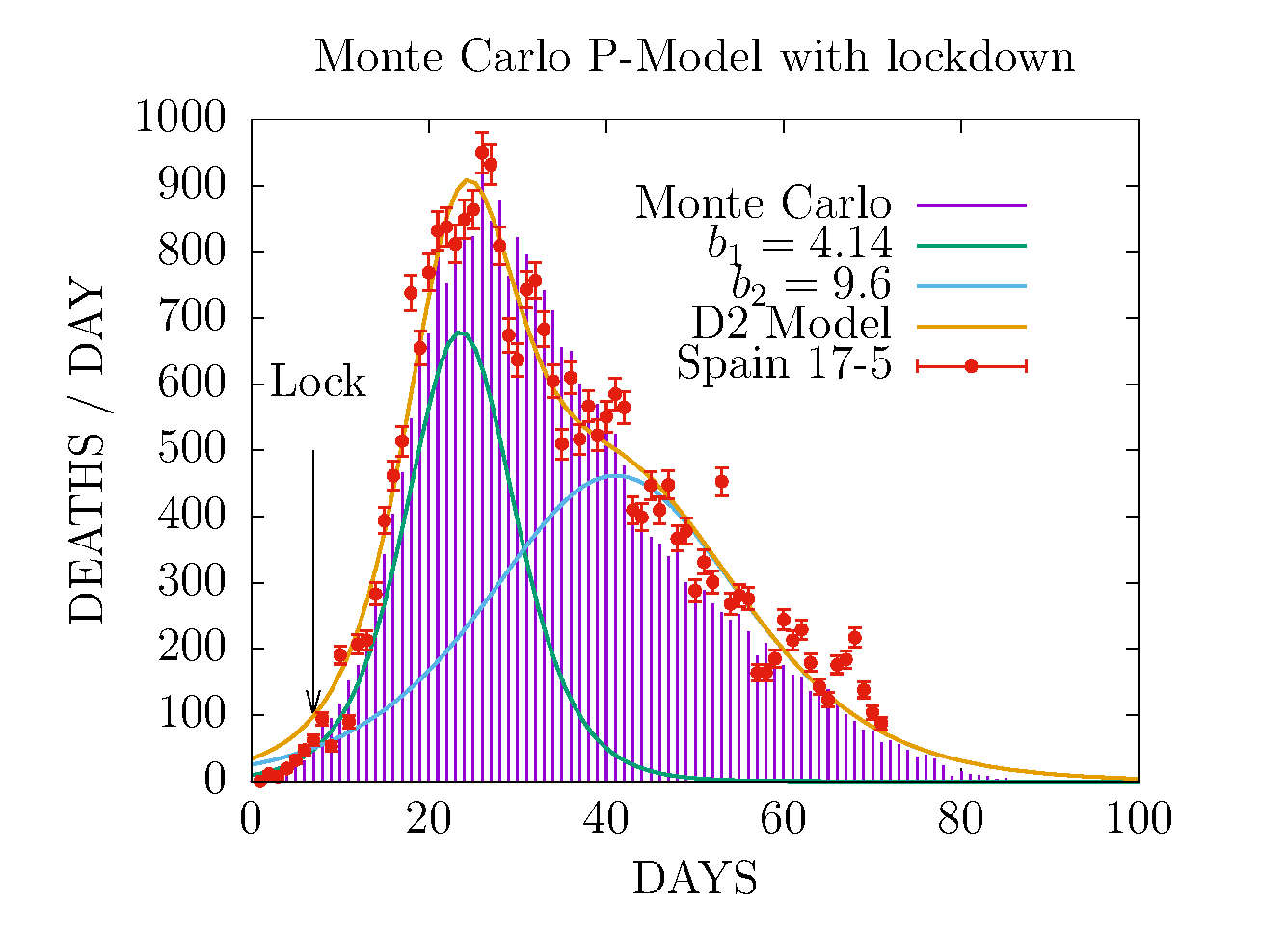
MODEL D2 AND MONTE CARLO - DEATHS-PER-DAY IN SPAIN 17 MAY
This Monte Carlo was fitted to data up to May 2
-
MODEL D2 AND MONTE CARLO - TOTAL DEATHS IN SPAIN 15 MAY
The Monte Carlo has been fitted to data up to May 2
-
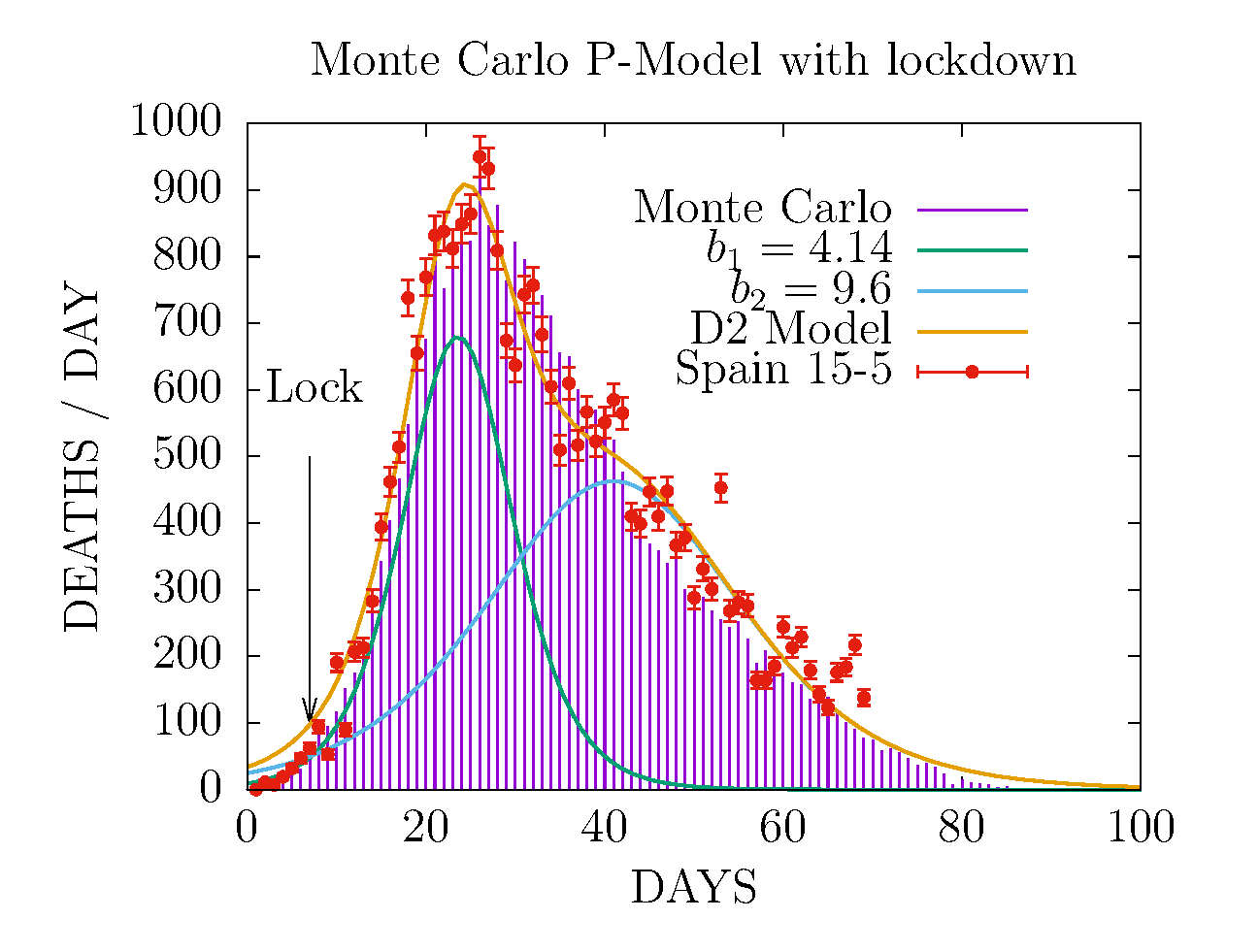
MODEL D2 AND MONTE CARLO - DEATHS-PER-DAY IN SPAIN 15 MAY
This Monte Carlo was fitted to data up to May 2
-
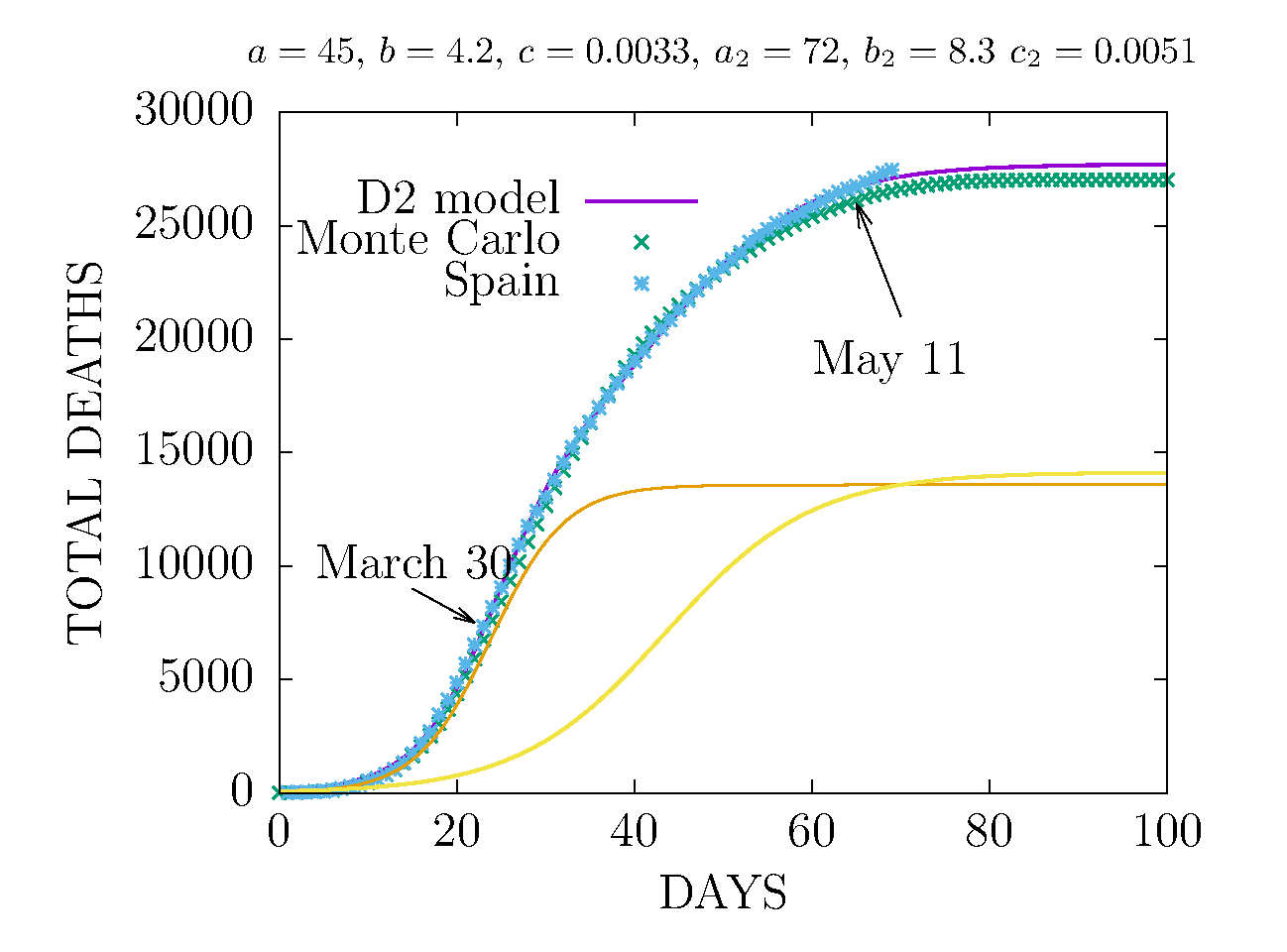
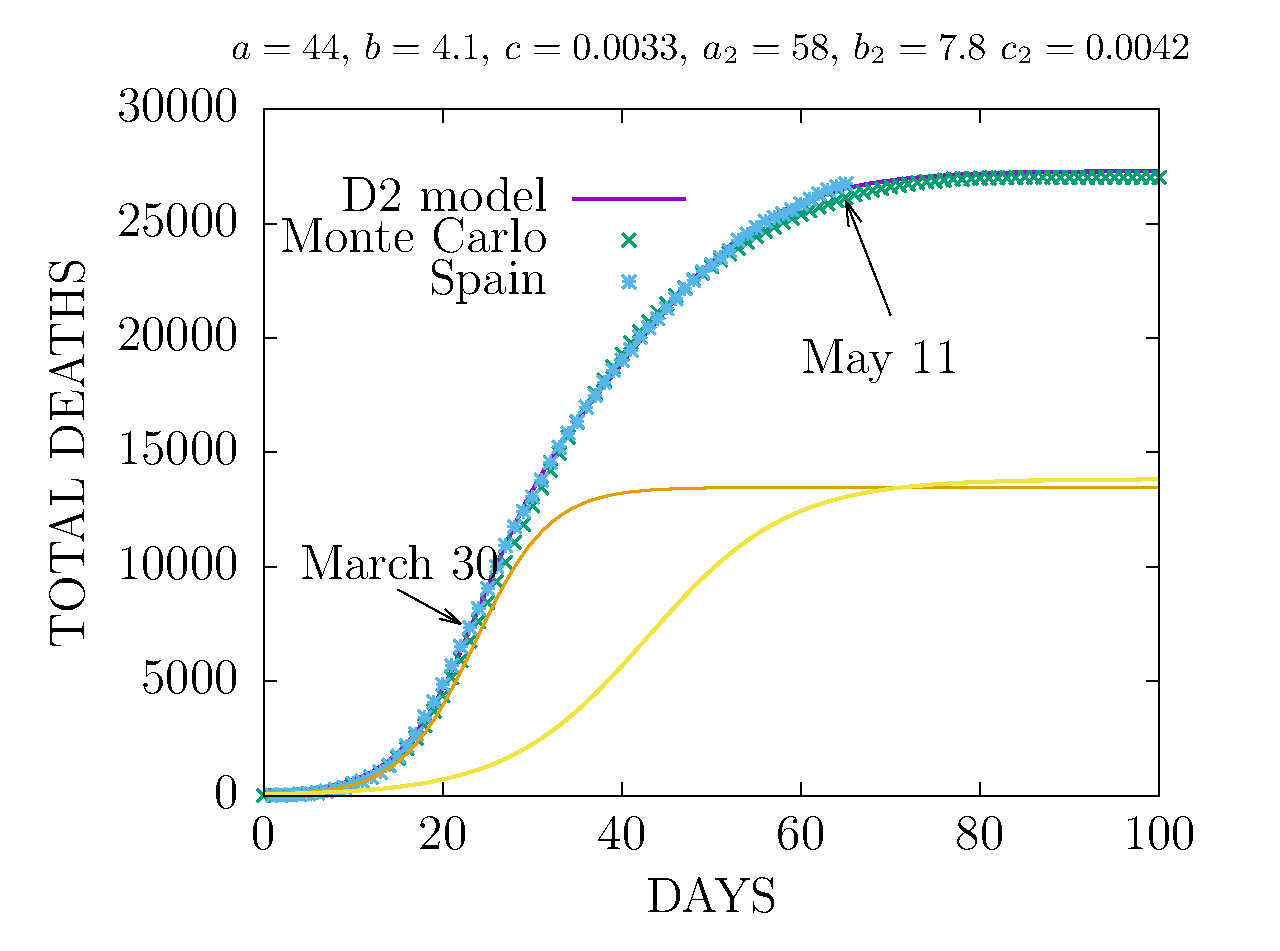
MODEL D2 AND MONTE CARLO - TOTAL DEATHS IN SPAIN 11 MAY
The Monte Carlo has been fitted to data up to May 2
-
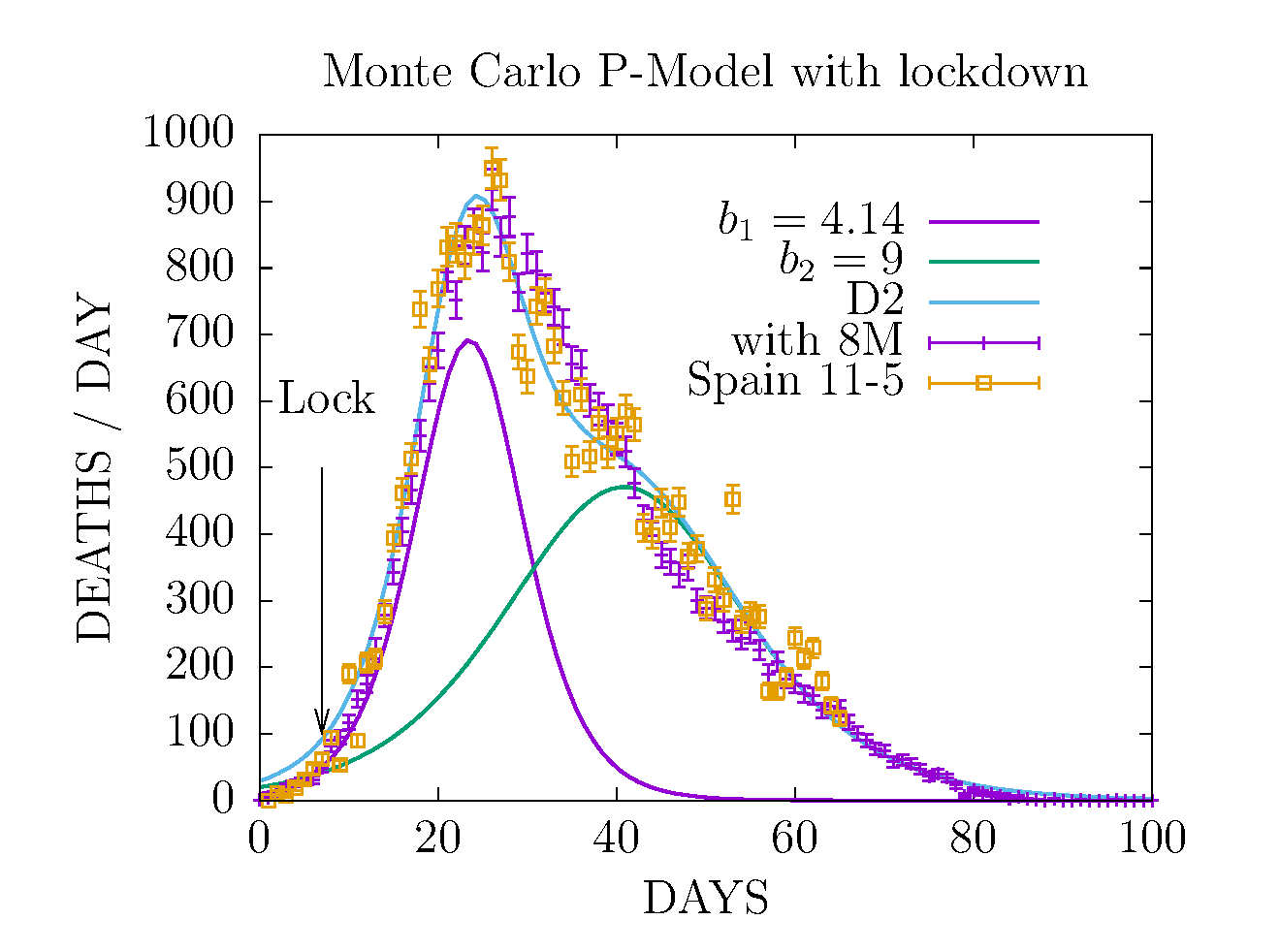
MODEL D2 AND MONTE CARLO - DEATHS-PER-DAY IN SPAIN 11 MAY
The Monte Carlo has been fitted to include
effects from 8M public events and lock-down
-
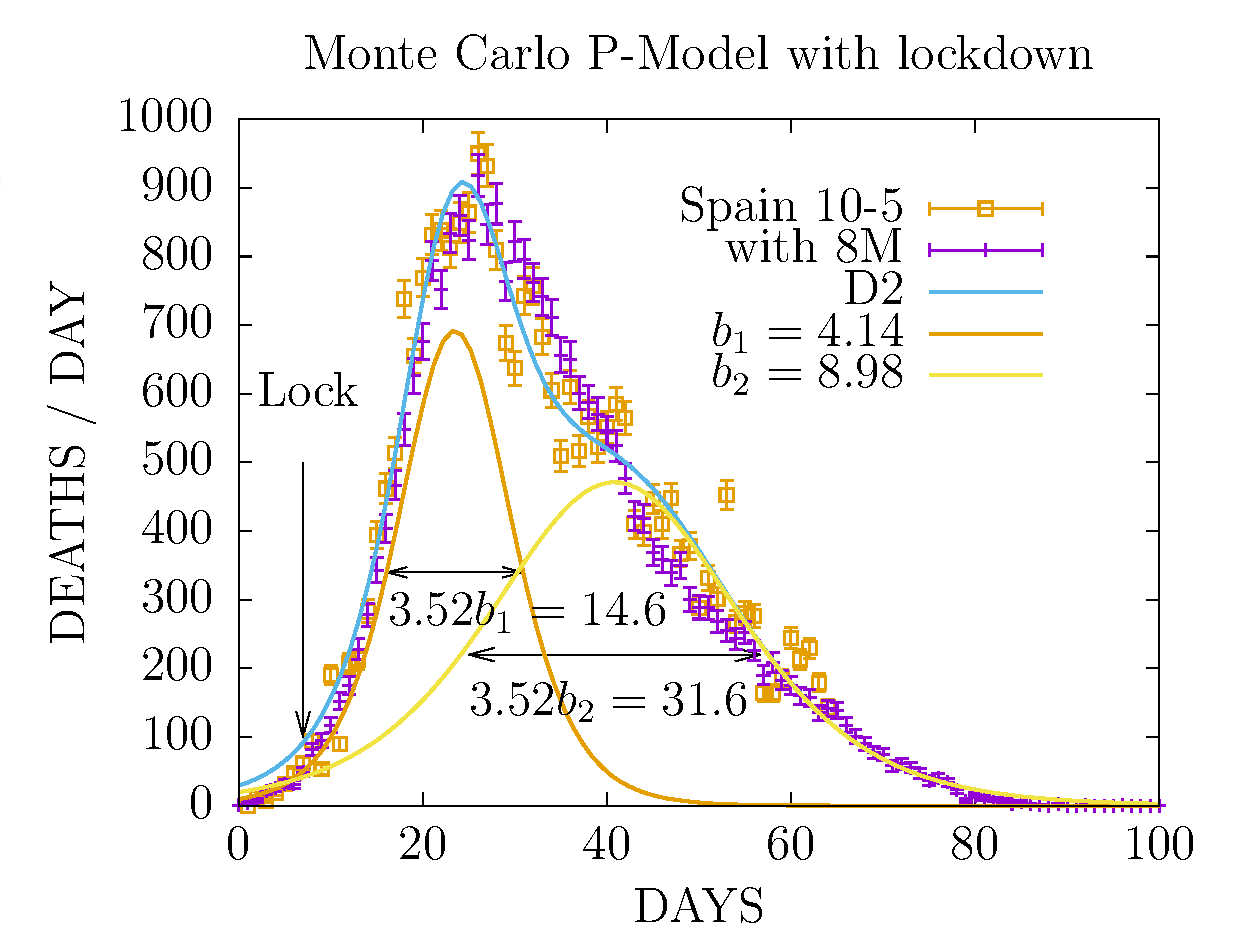
MODEL D2 AND MONTE CARLO - DEATHS-PER-DAY IN SPAIN 10 MAY
The Monte Carlo has been fitted to include
effects from 8M public events and lock-down
-
MODEL D2 AND MONTE CARLO - DEATHS-PER-DAY IN SPAIN 6 MAY
The Monte Carlo has been fitted to include
effects from 8M public events and lock-down
-
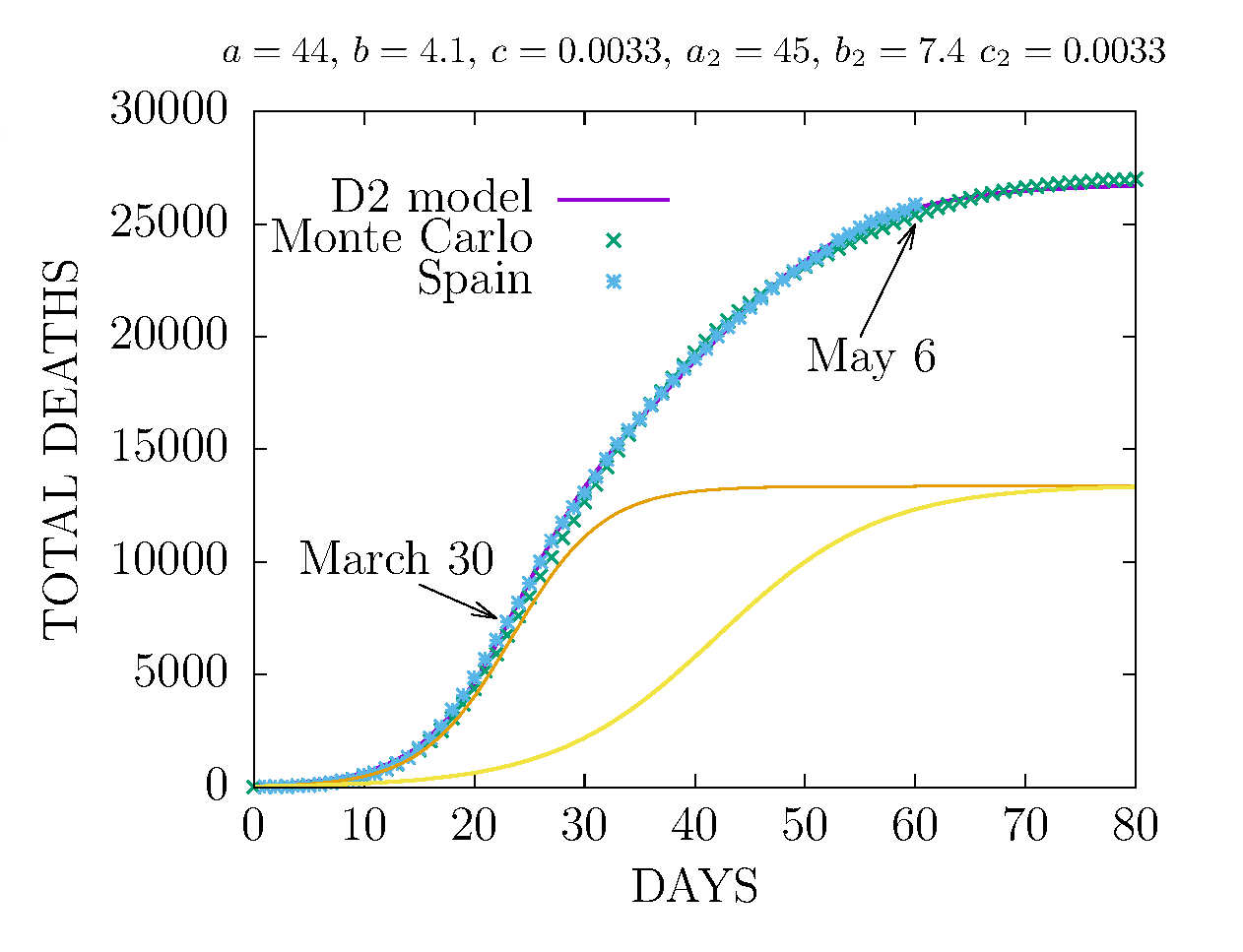
MODEL D2 AND MONTE CARLO - TOTAL DEATHS IN SPAIN 6 MAY
The Monte Carlo has been fitted to include
effects from 8M public events and lock-down
-
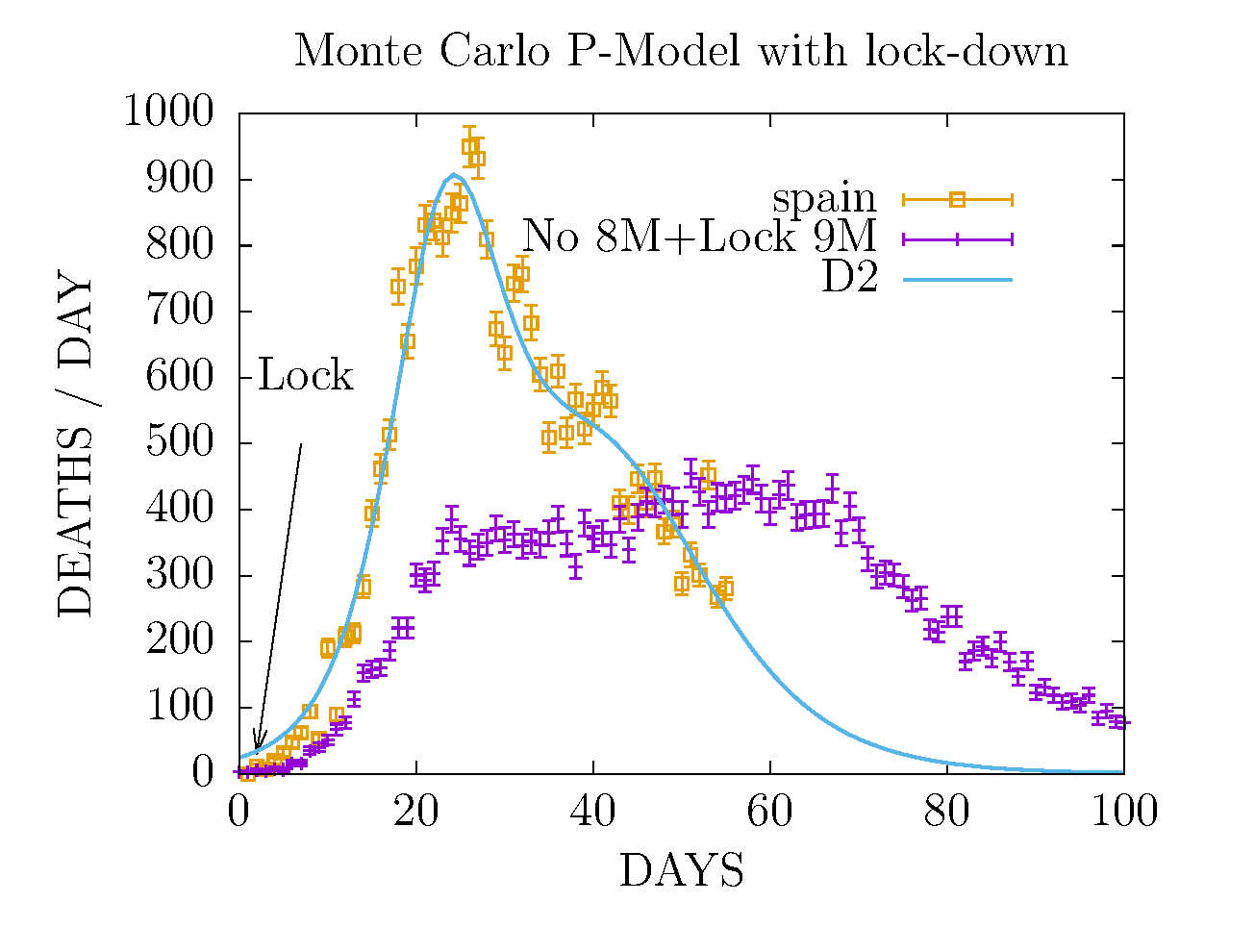
MODEL D2 AND MONTE CARLO - DEATHS IN SPAIN 1 MAY
The Monte Carlo has been re-fitted to include
effects from 8M public events and lock-down
seven days after it.
This figure shows the Monte carlo without the 8M event
and with lock-down the following day 9M.
-
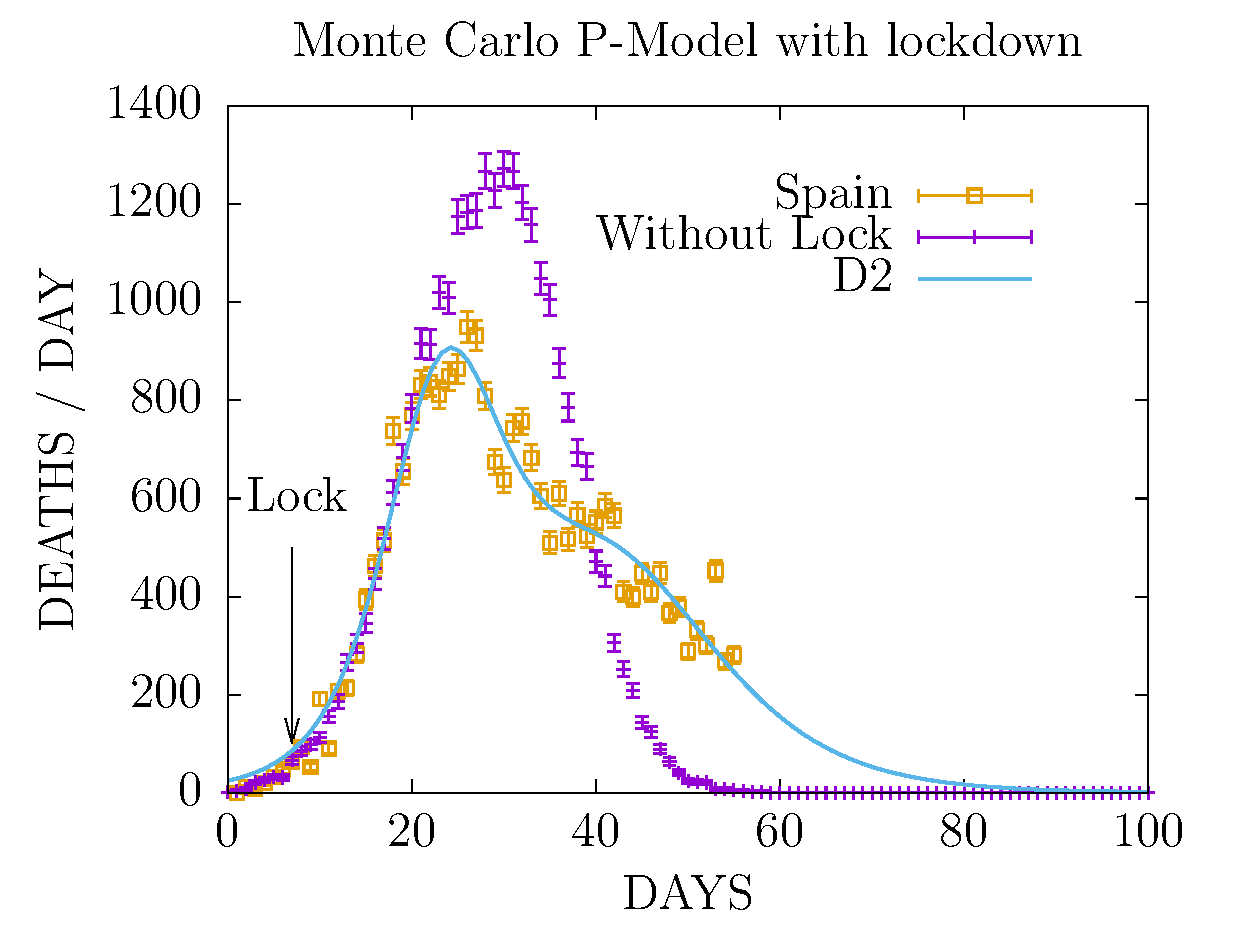
MODEL D2 AND MONTE CARLO - DEATHS IN SPAIN 1 MAY
The Monte Carlo has been re-fitted to include
effects from 8M public events and lock-down
seven days after it.
This figure shows the Monte carlo without the lock-down effect.
-
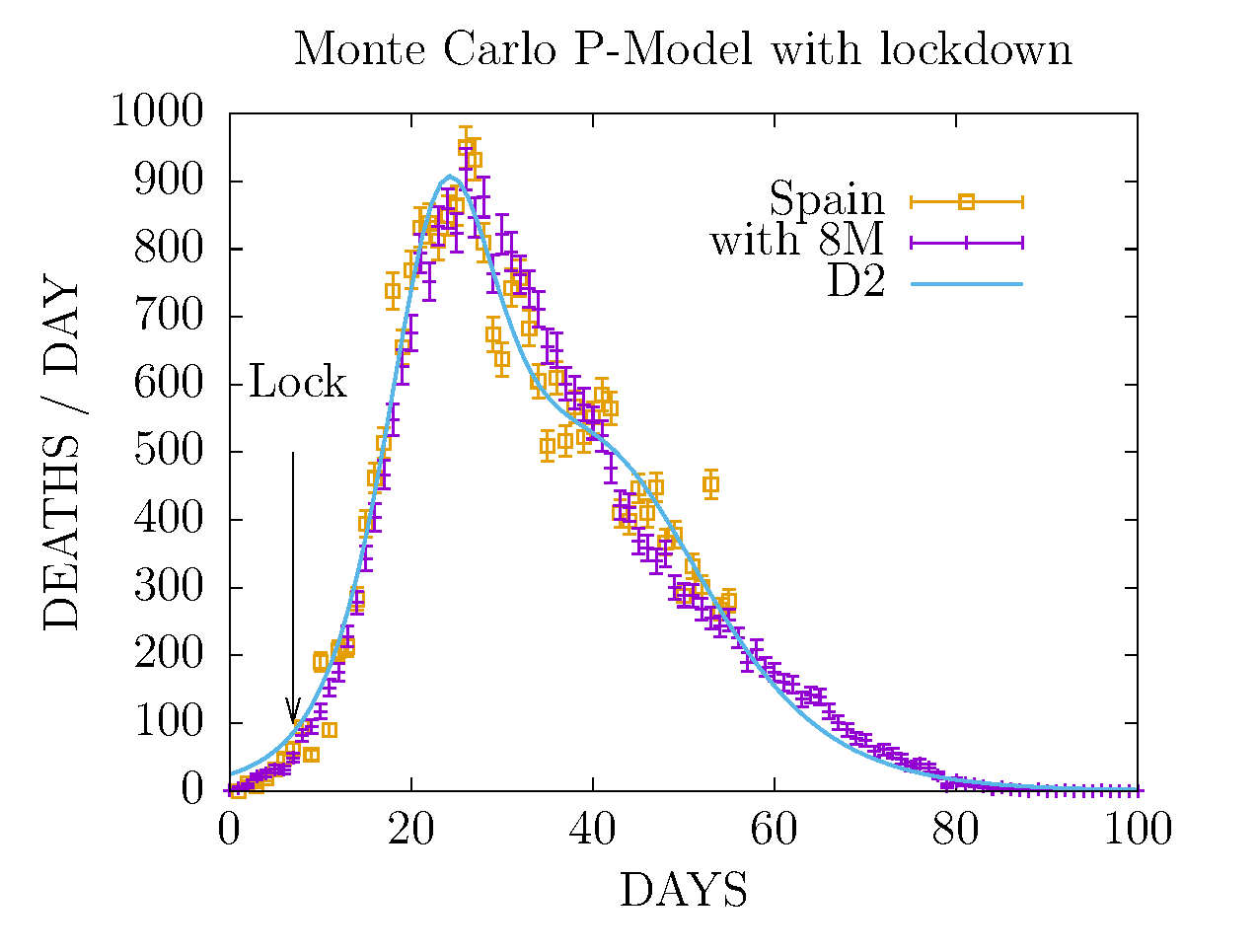
MODEL D2 AND MONTE CARLO - DEATHS IN SPAIN 1 MAY
The new Monte Carlo has been re-fitted to include
effects from 8M public events and lock-down
seven days after it.
This figure shows the Monte Carlo without 8M events.
-
MODEL D2 AND MONTE CARLO - DEATHS IN SPAIN 1 MAY
The Monte Carlo has been re-fitted to include
effects from 8M public events and lock-down
seven days after it.
-
MODEL D2 AND MONTE CARLO - DEATHS IN SPAIN 30 APRIL
-
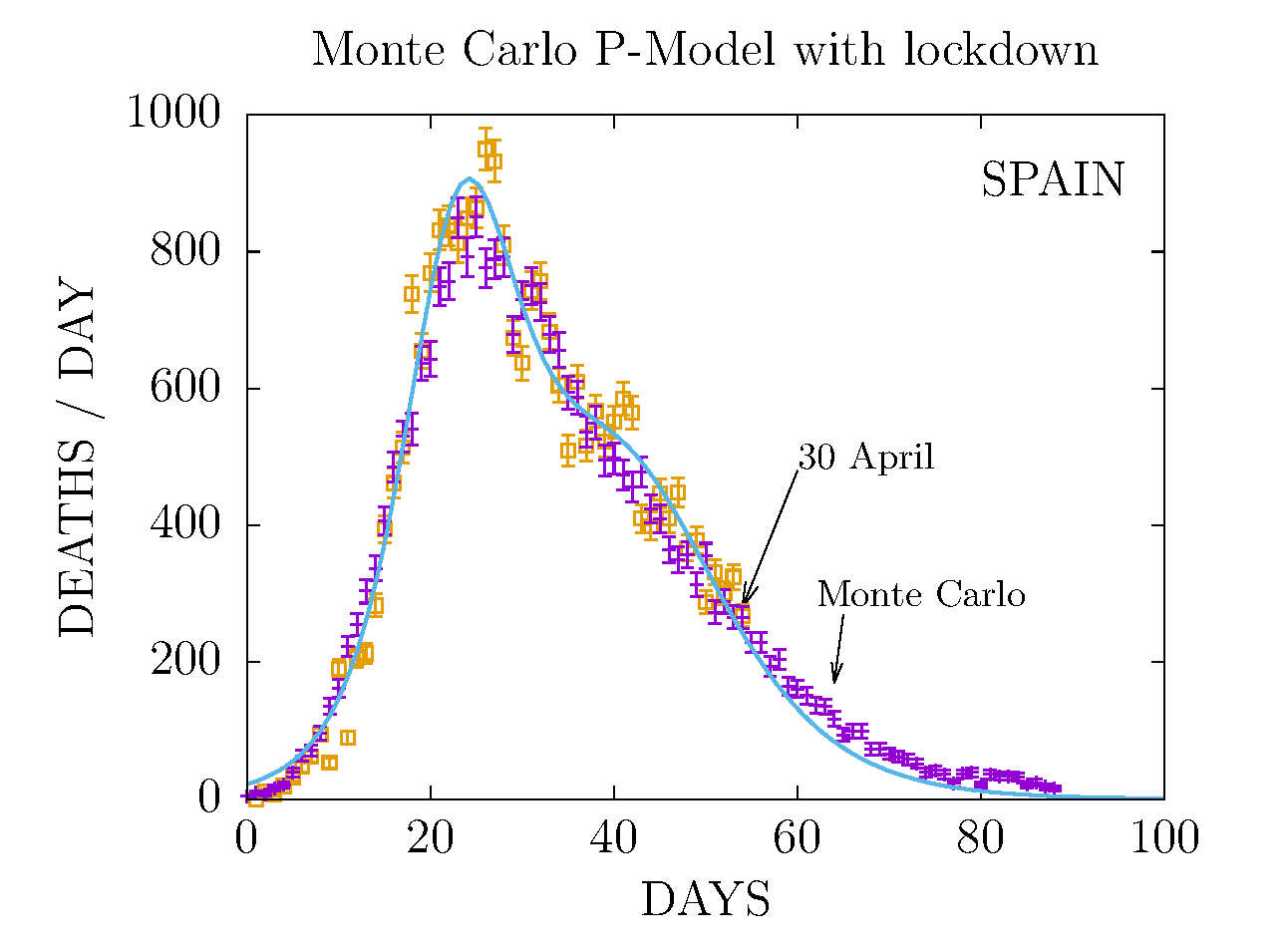
DEATHS PER DAY IN SPAIN APRIL 30 AND MONTE CARLO P-MODEL
Results from the Plack model are points computed with Monte Carlo
simulation in a lattice with temperature T, representing the average
movility (or energy) of the individuals
-
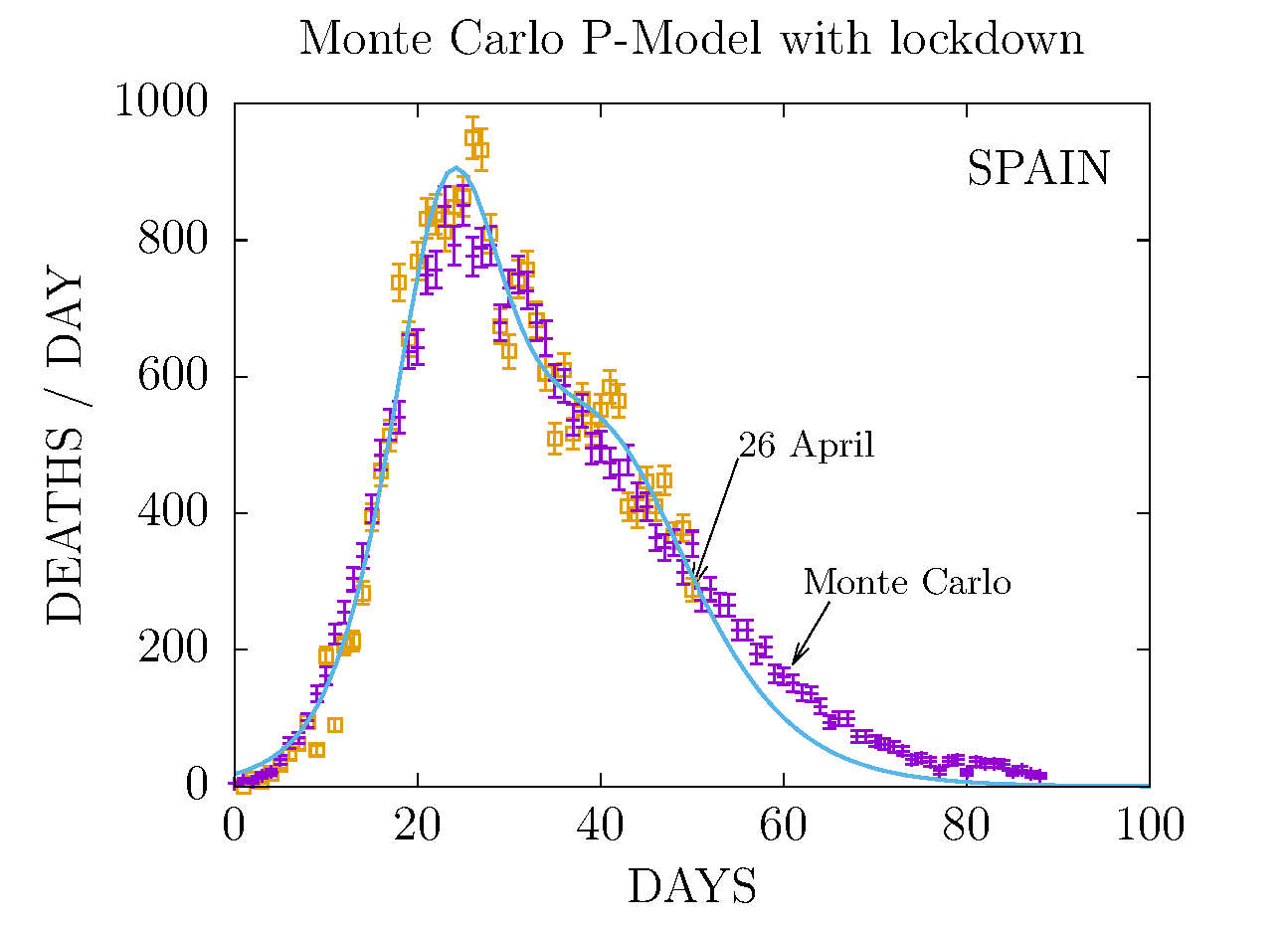
DEATHS PER DAY IN SPAIN APRIL 26 AND MONTE CARLO P-MODEL
Results from the Plack model are points computed with Monte Carlo
simulation in a lattice with temperature T, representing the average
movility (or energy) of the individuals
-
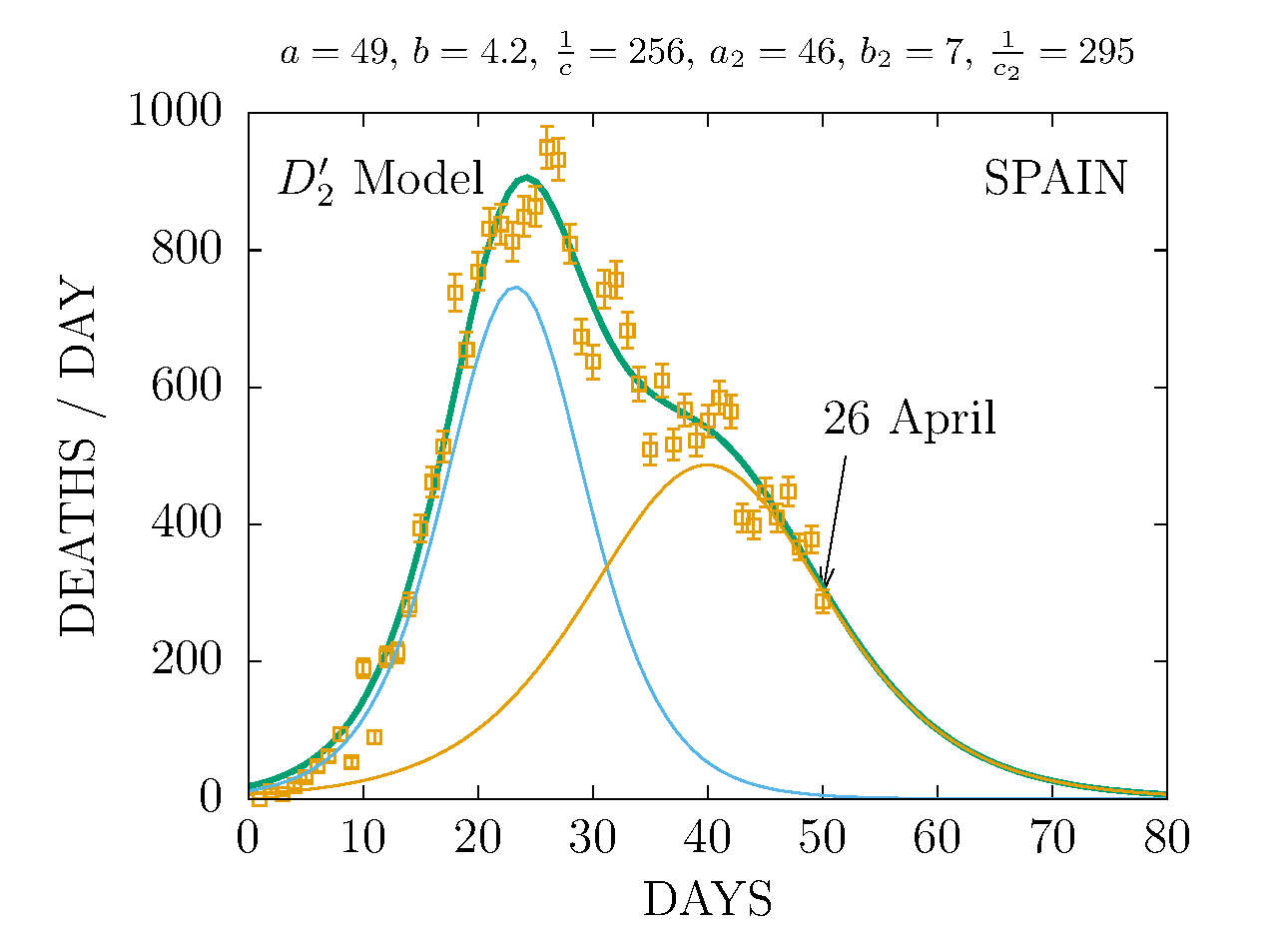
DEATHS PER DAY IN SPAIN APRIL 26 - MODEL D'2
-
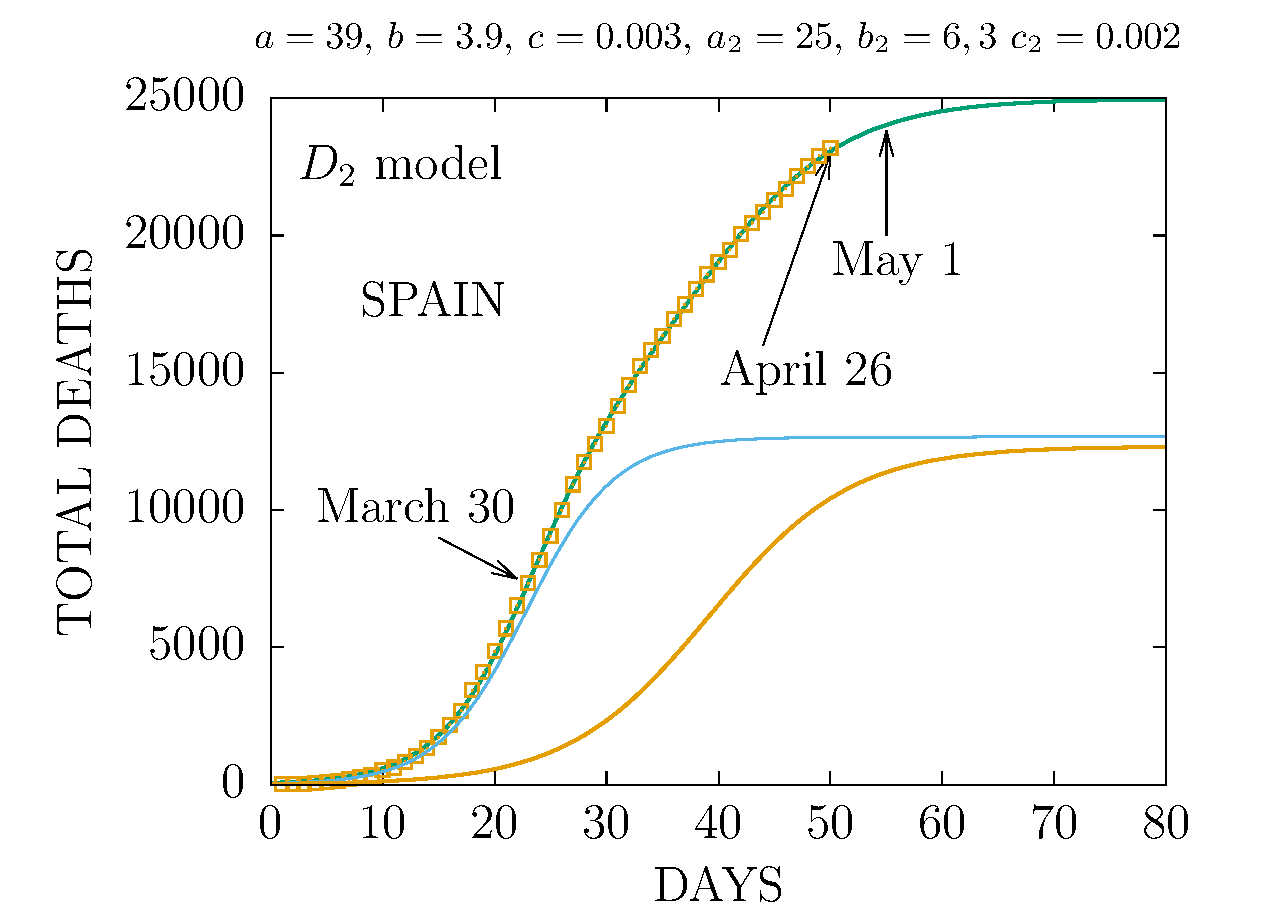
MODEL D2 DEATHS IN SPAIN 26 APRIL
The data are more compatible with the sum of two D-functions with different parameters.
-
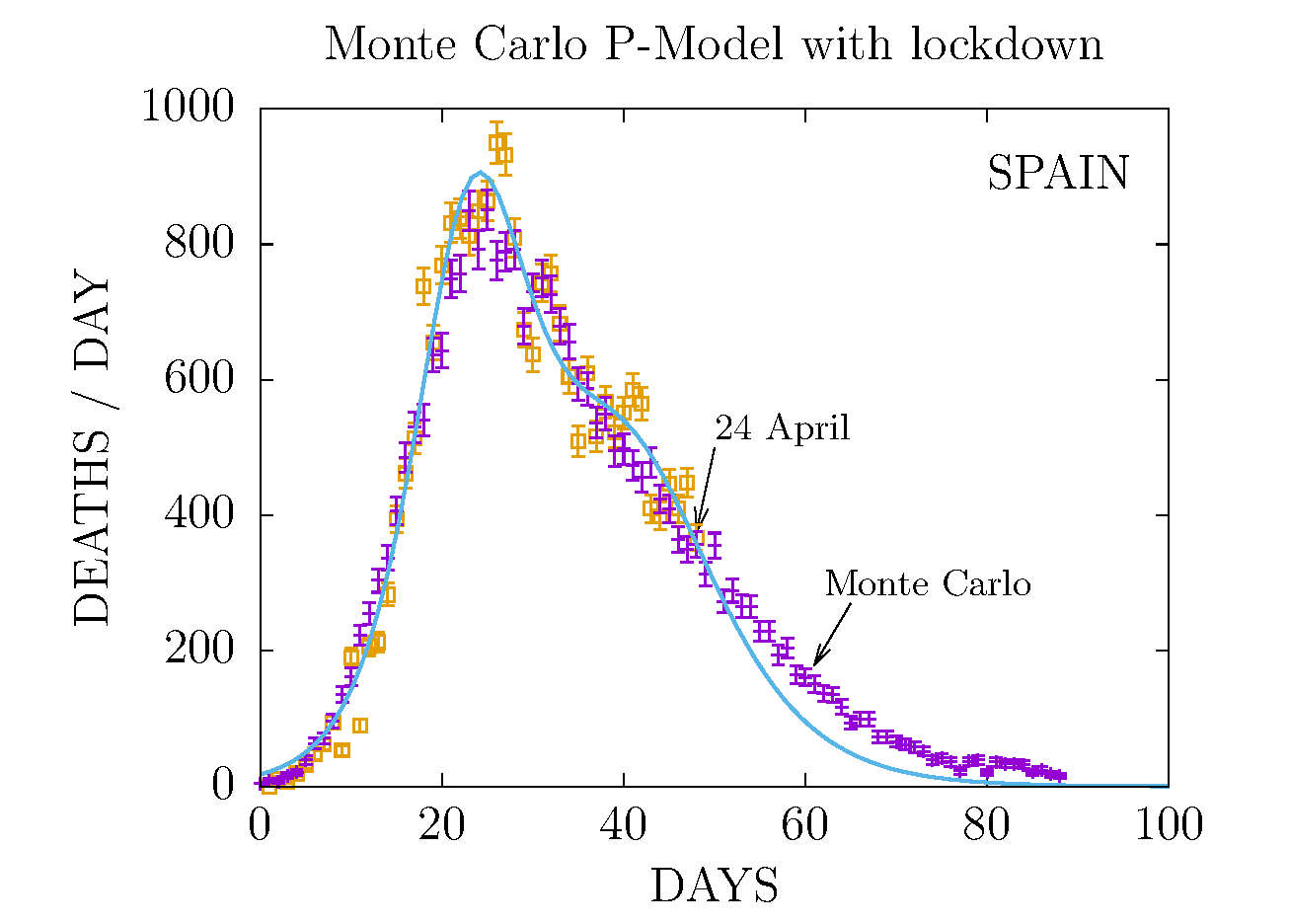
DEATHS PER DAY IN SPAIN APRIL 24 AND MONTE CARLO P-MODEL
Results from the Plack model are points computed with Monte Carlo
simulation in a lattice with temperature T, representing the average
movility (or energy) of the individuals
-
DEATHS PER DAY IN SPAIN APRIL 24 - MODEL D'2
-
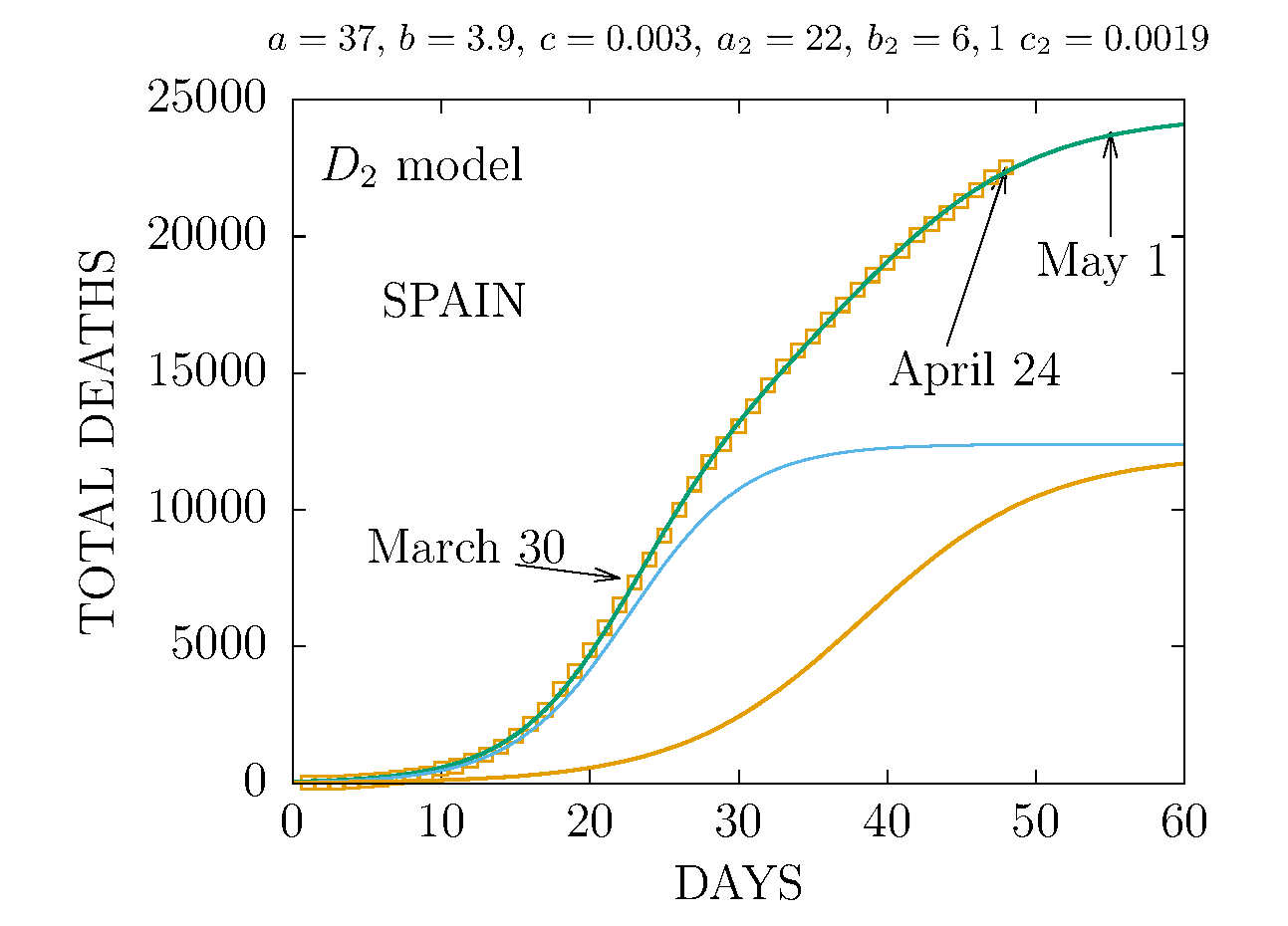
MODEL D2 DEATHS IN SPAIN 24 APRIL
The data are more compatible with the sum of two D-functions with different parameters.
-
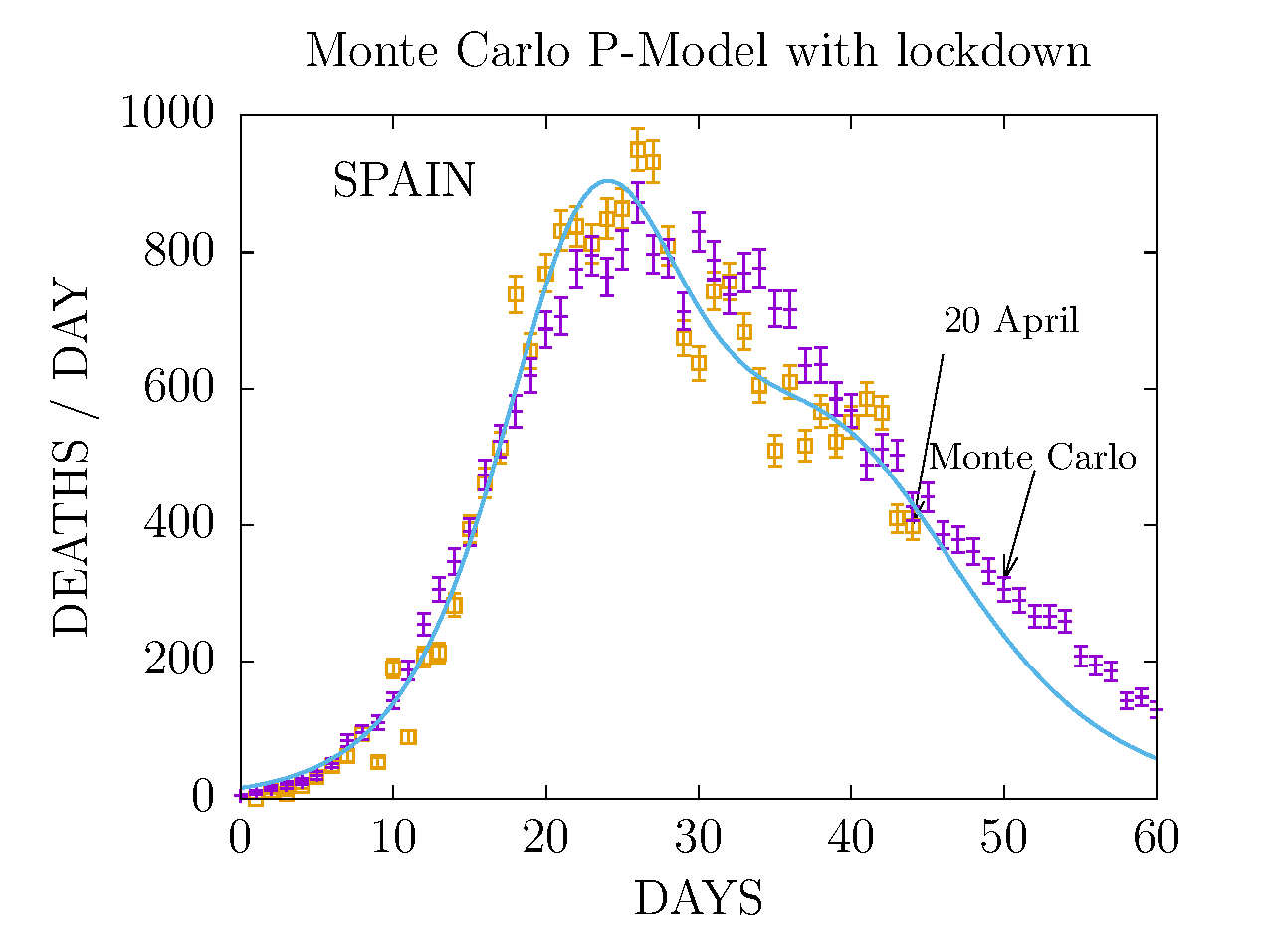
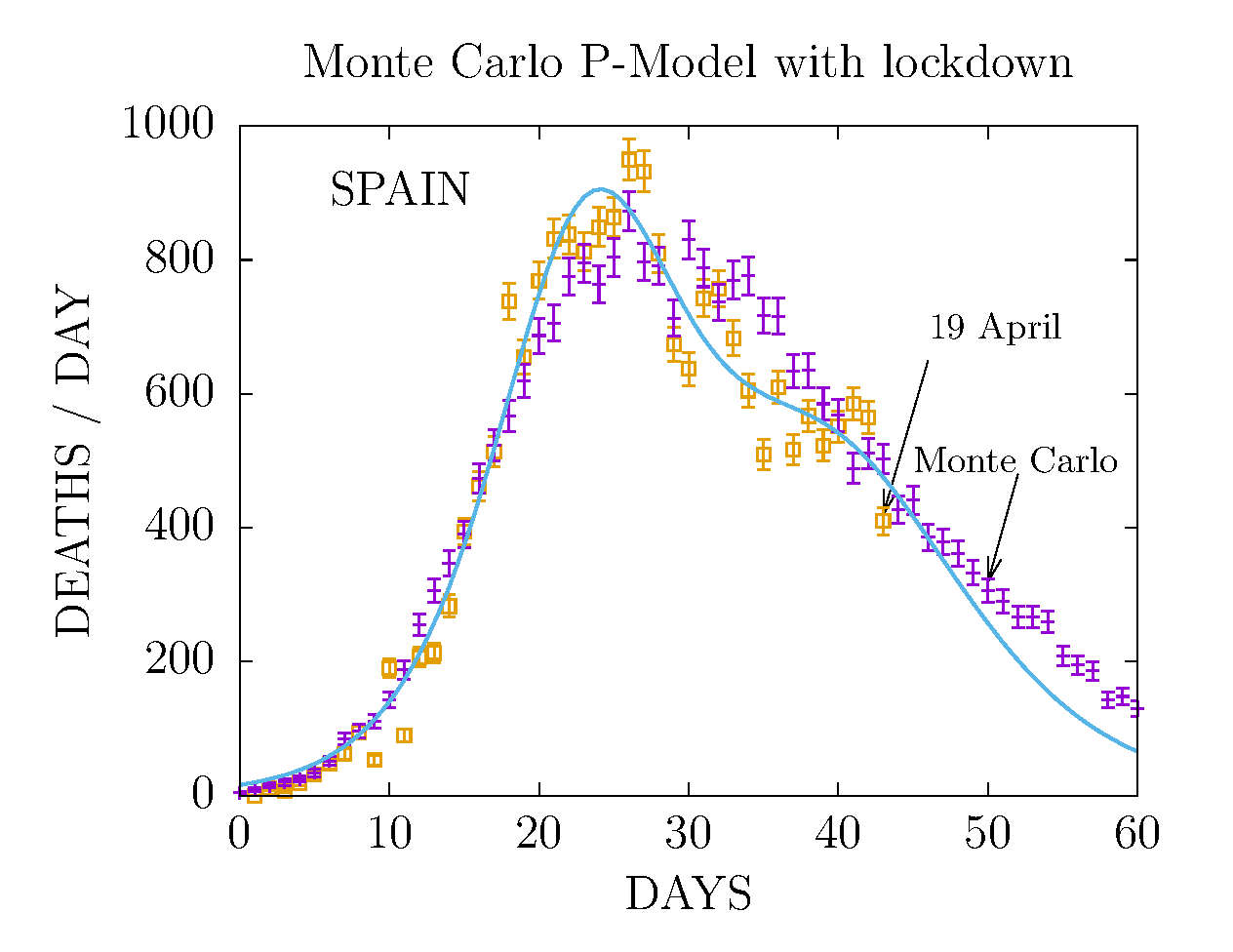
DEATHS PER DAY IN SPAIN APRIL 20 AND NEW MONTE CARLO P-MODEL
Results from the Plack model are points computed with Monte Carlo
simulation in a lattice with temperature T, representing the average
movility (or energy) of the individuals
-
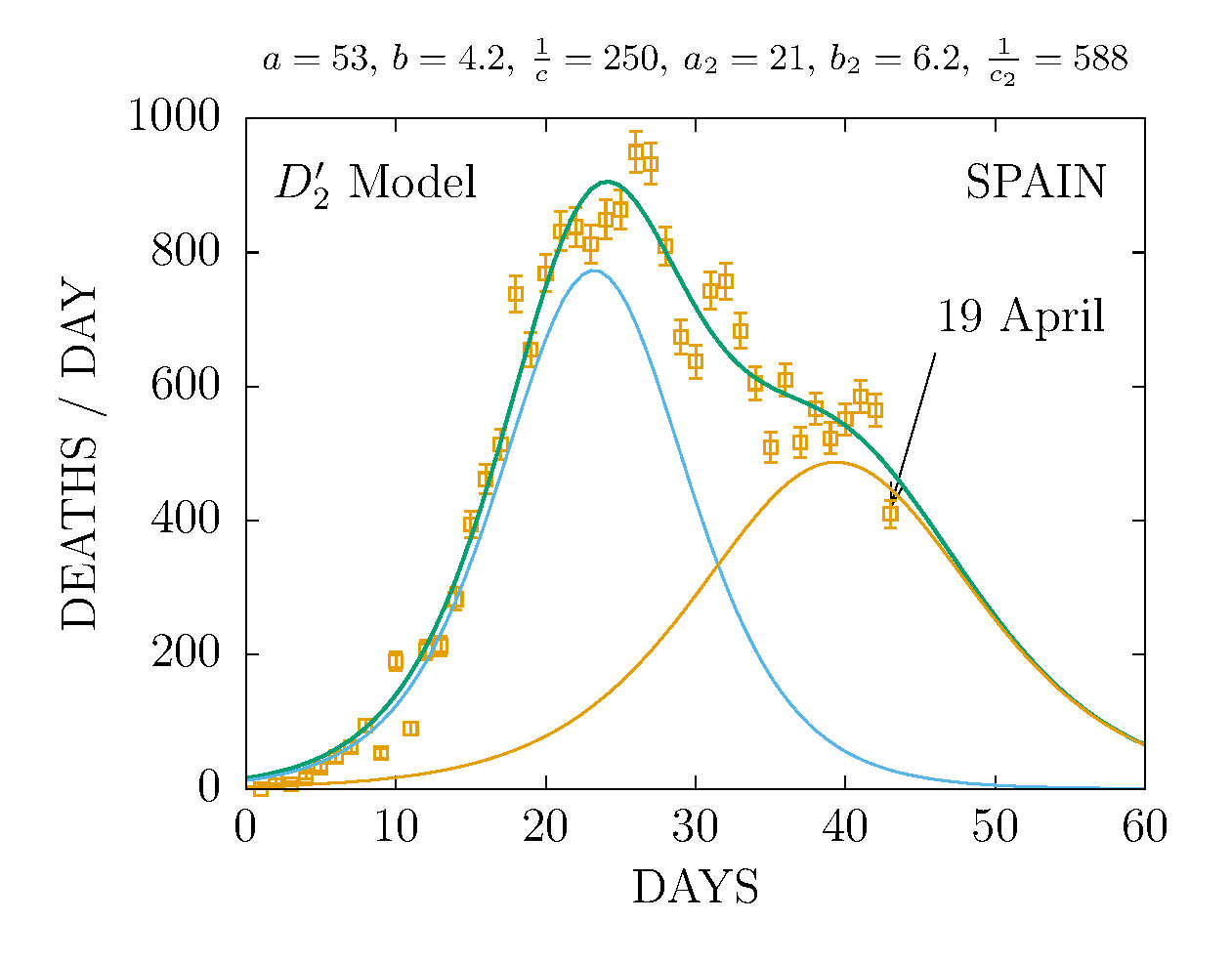
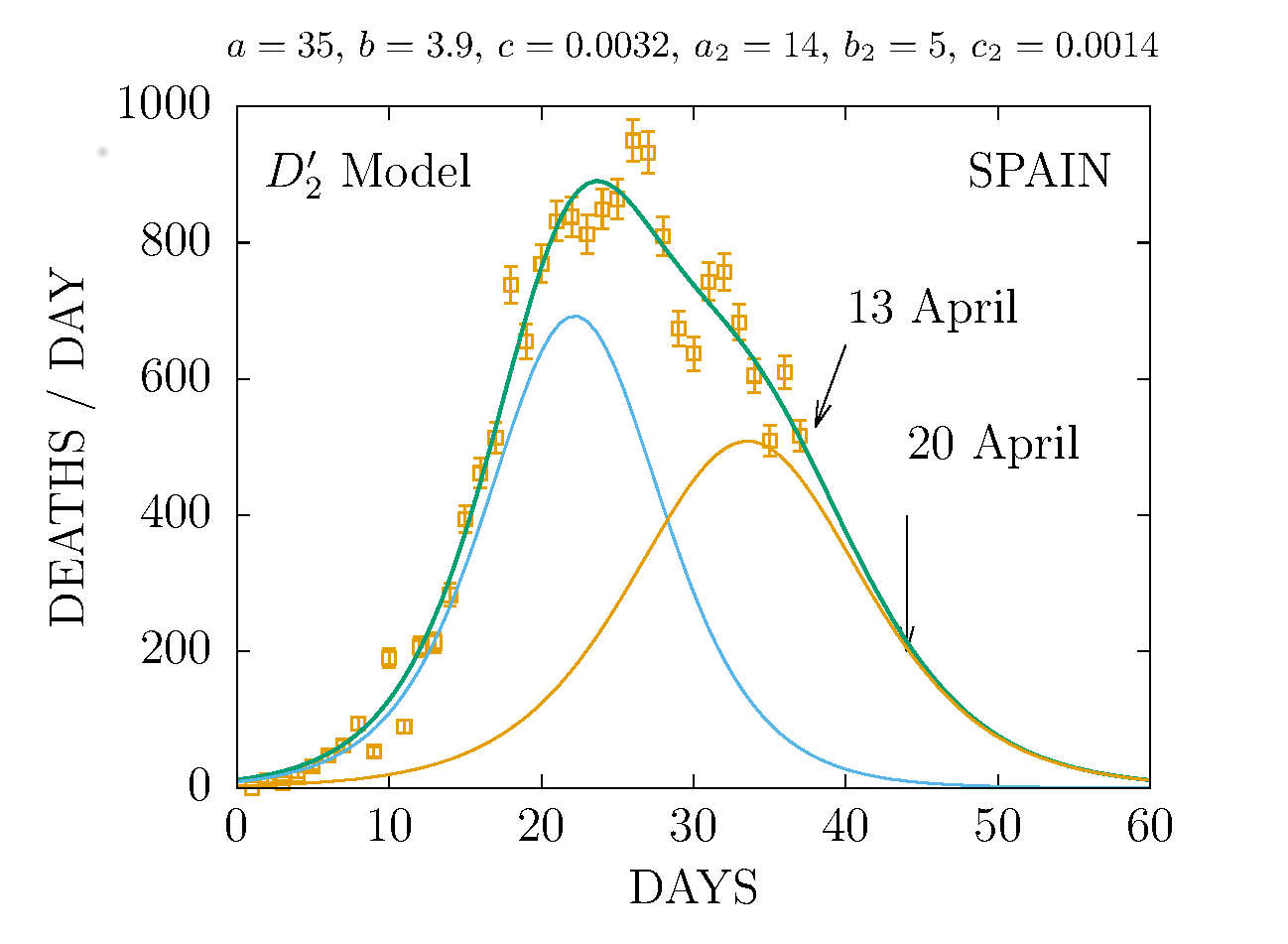
DEATHS PER DAY IN SPAIN APRIL 20 - MODEL D'2
-
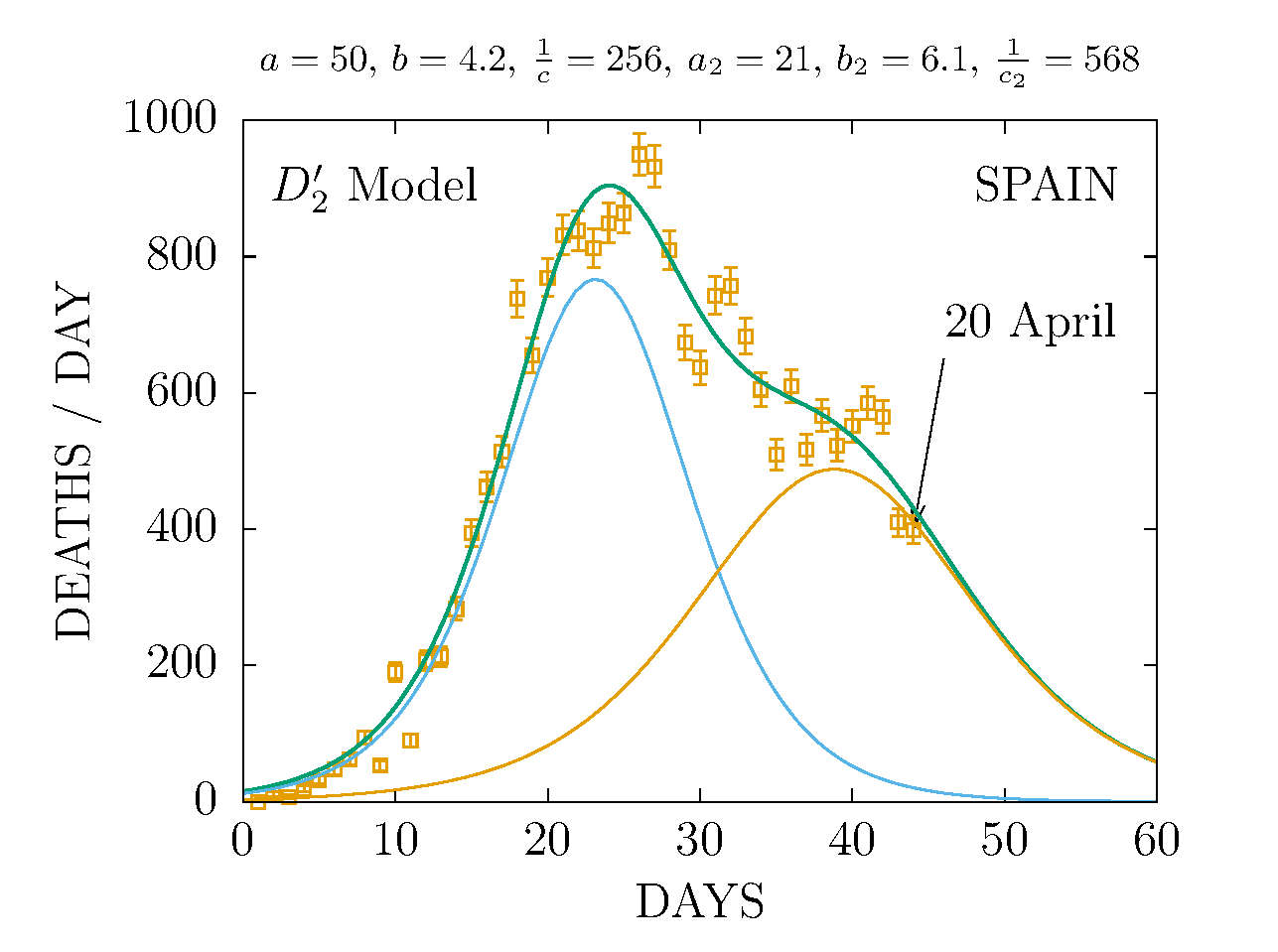
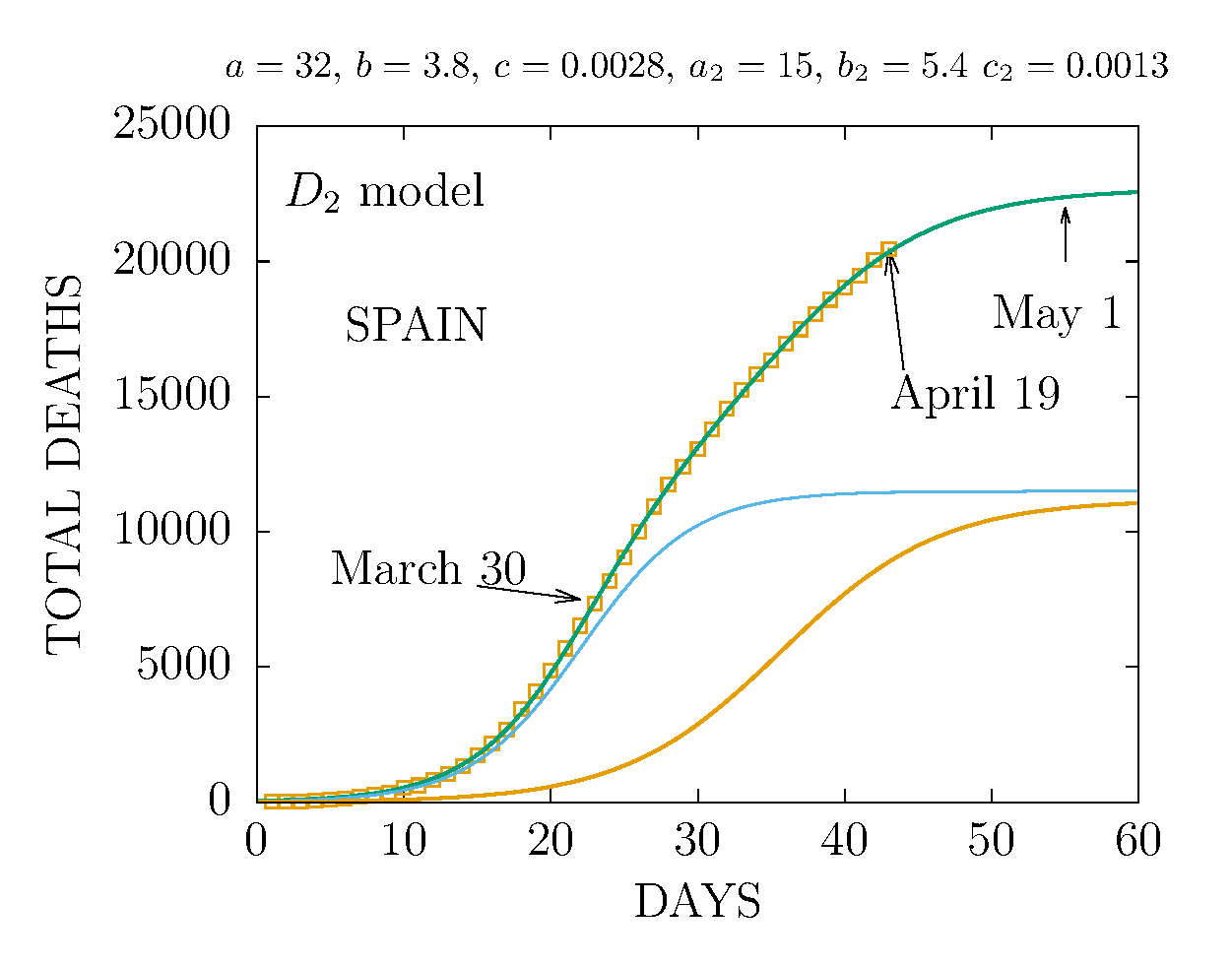
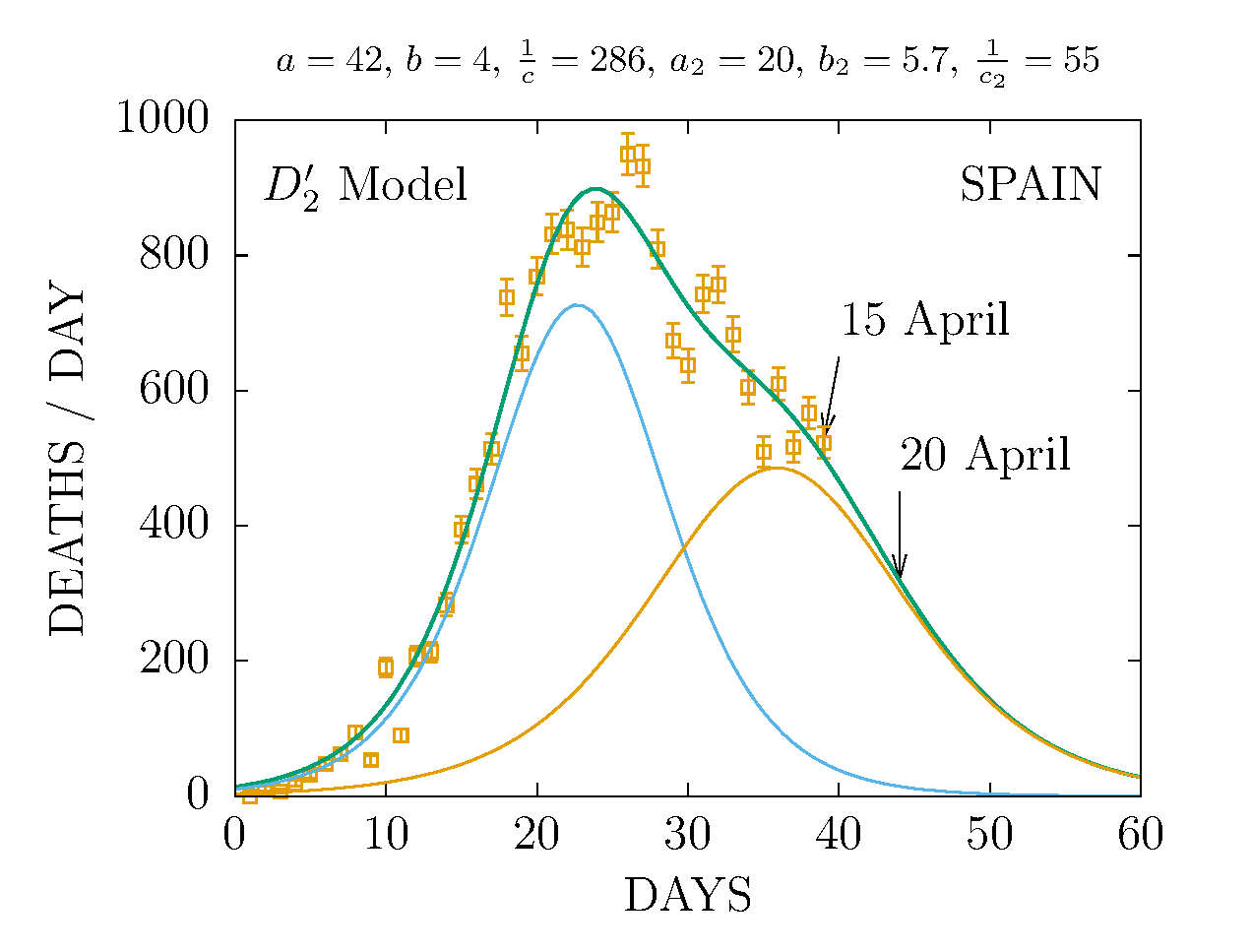
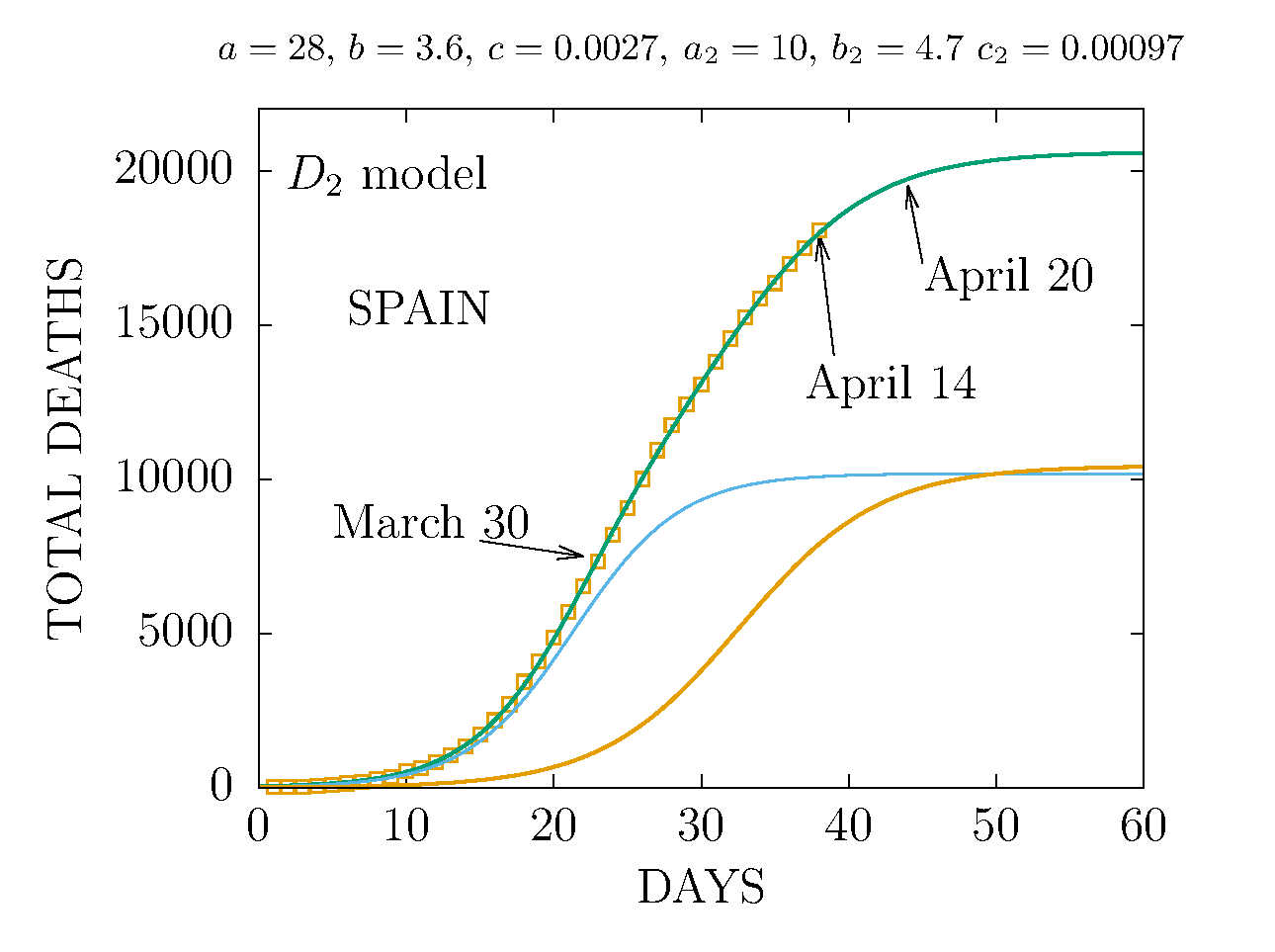
MODEL D2 DEATHS IN SPAIN 20 APRIL
The data are more compatible with the sum of two D-functions with different parameters.
-
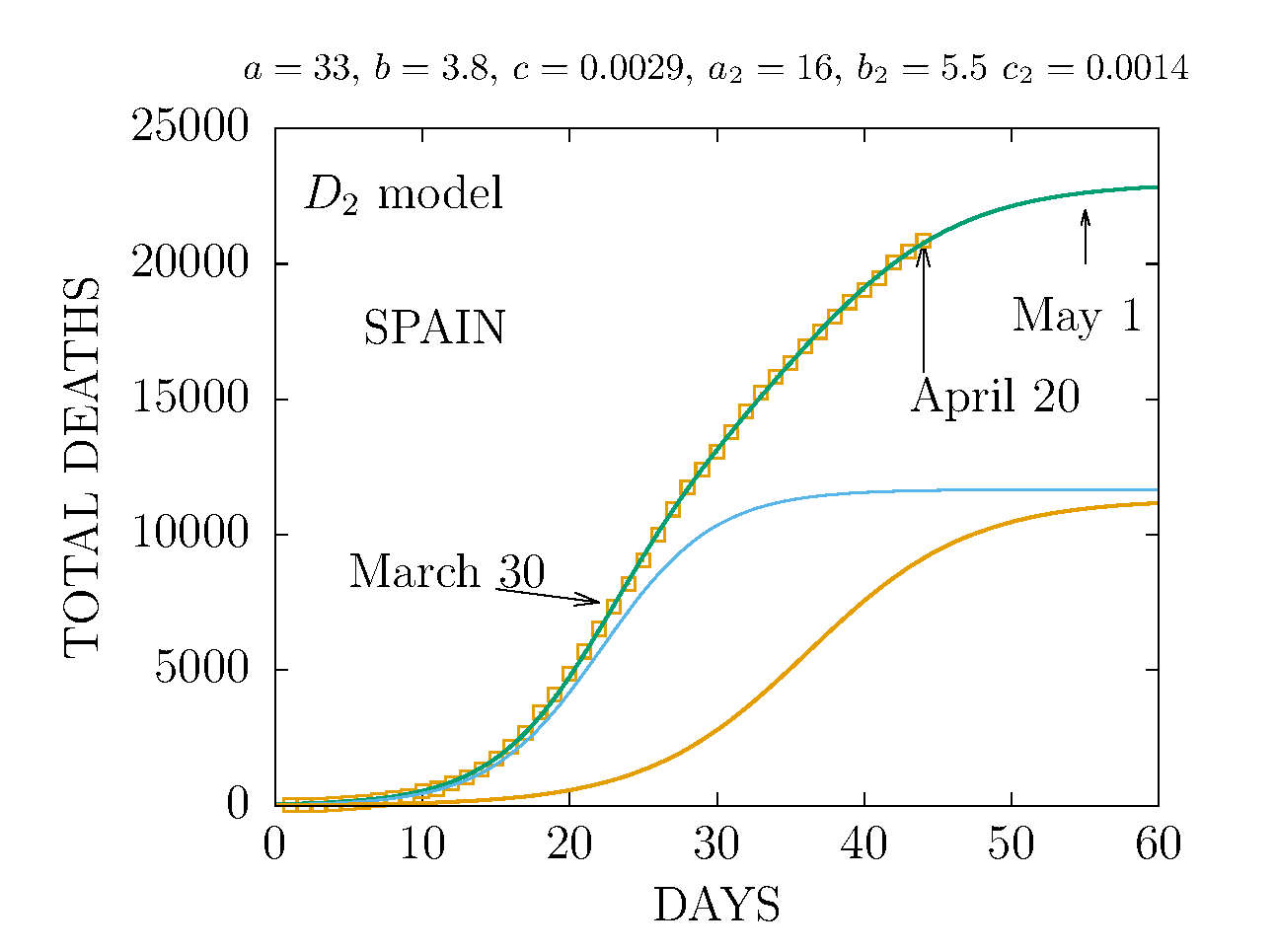
DEATHS PER DAY IN SPAIN APRIL 19 AND NEW MONTE CARLO P-MODEL
Results from the Plack model are points computed with Monte Carlo
simulation in a lattice with temperature T, representing the average
movility (or energy) of the individuals
-
DEATHS PER DAY IN SPAIN APRIL 19 - MODEL D'2
-
MODEL D2 DEATHS IN SPAIN 19 APRIL
The data are more compatible with the sum of two D-functions with different parameters.
-
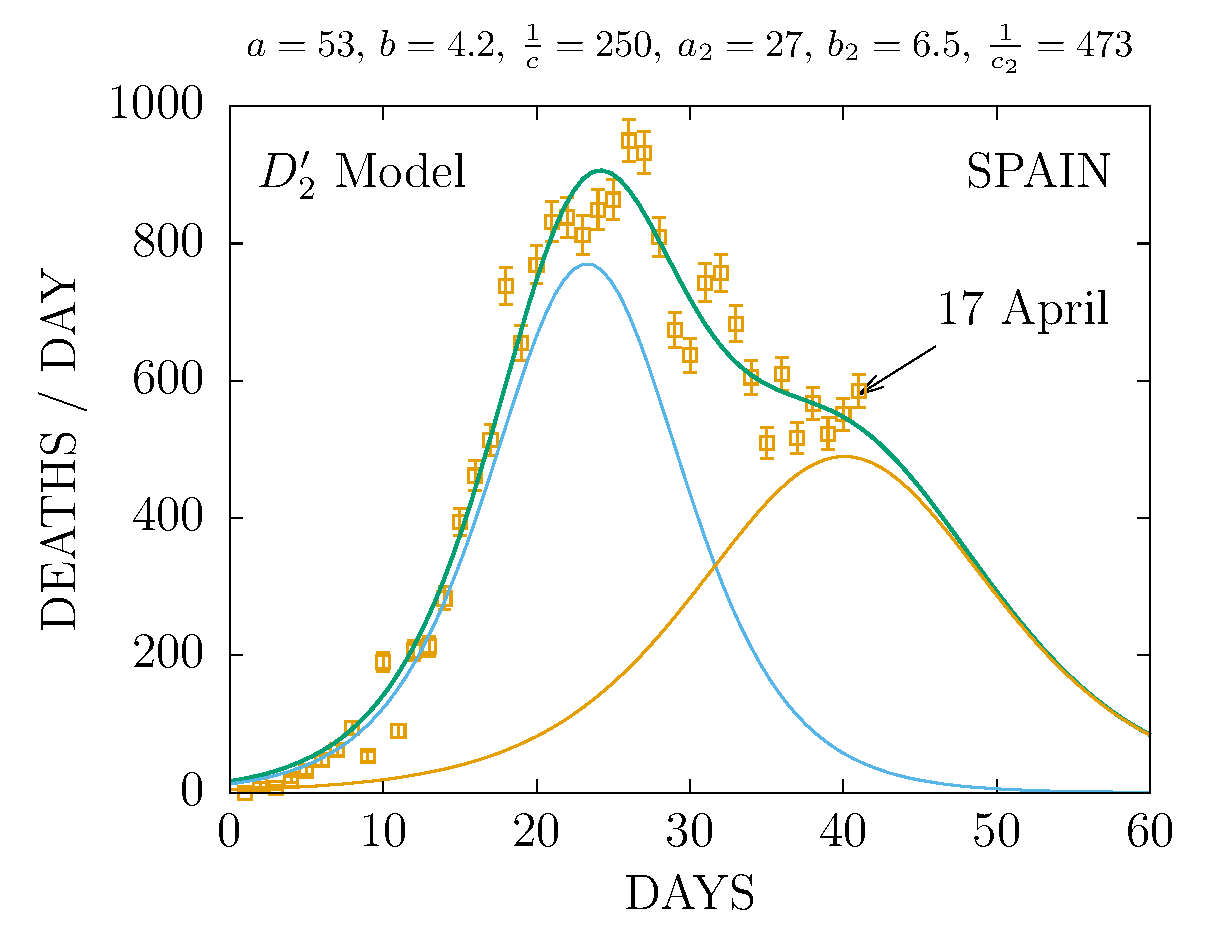
DEATHS PER DAY IN SPAIN APRIL 17 - MODEL D'2
-
MODEL D2 DEATHS IN SPAIN 17 APRIL
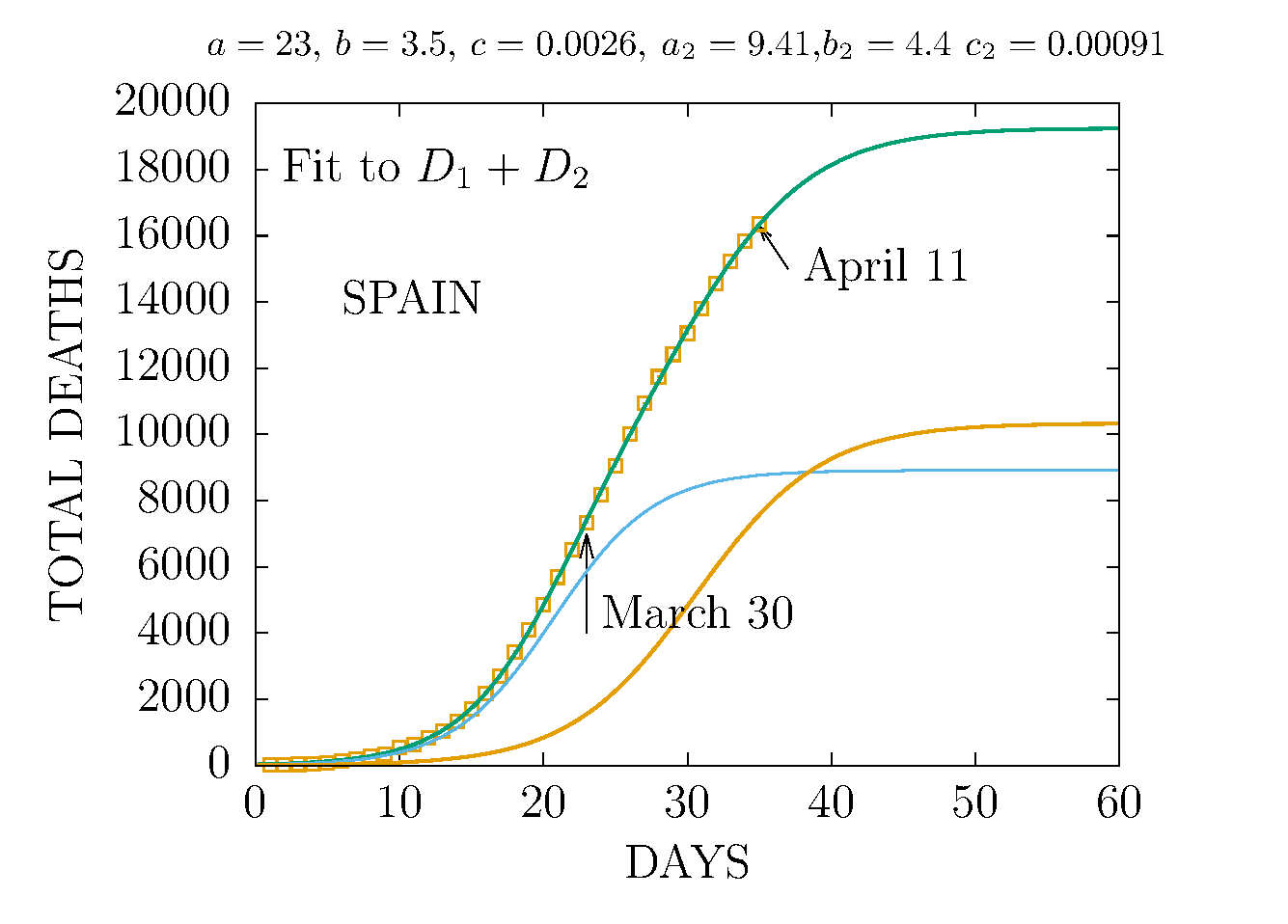
THE D2 MODEL ASUMES TWO CHANNELS OF INFECTION 1 and 2 with different parameters. Here the fit is made to the total deaths. The data are more compatible with the sum of two D-functions with different parameters.
-
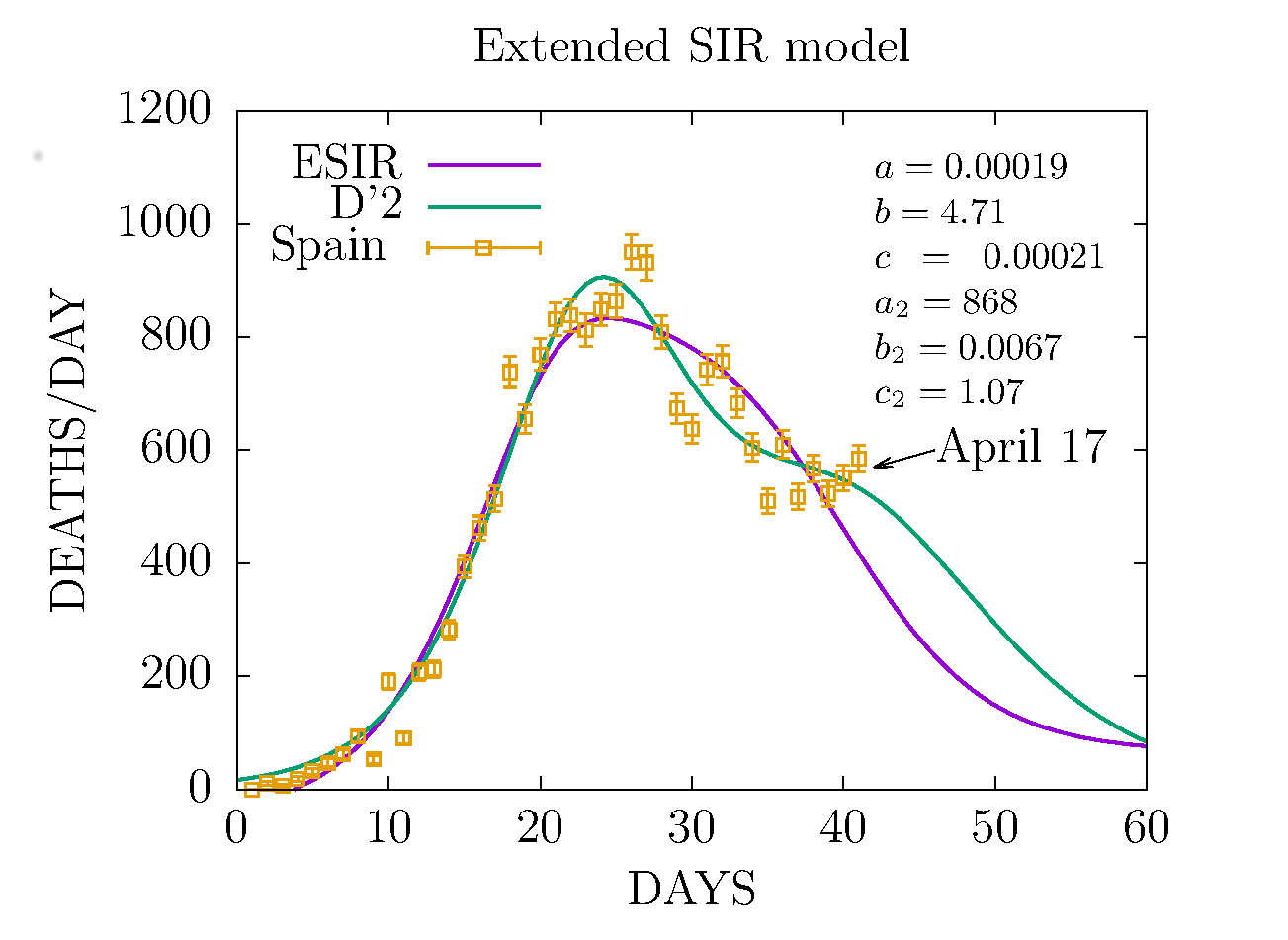
DEATHS PER DAY IN SPAIN APRIL 17 - EXTENDED SIR MODEL VS. D'2 MODEL
WE COMPARE THE NEW EXTENDED SIR MODEL WITH THE D'2 MODEL
THEY GIVE SIMILAR RESULTS
-
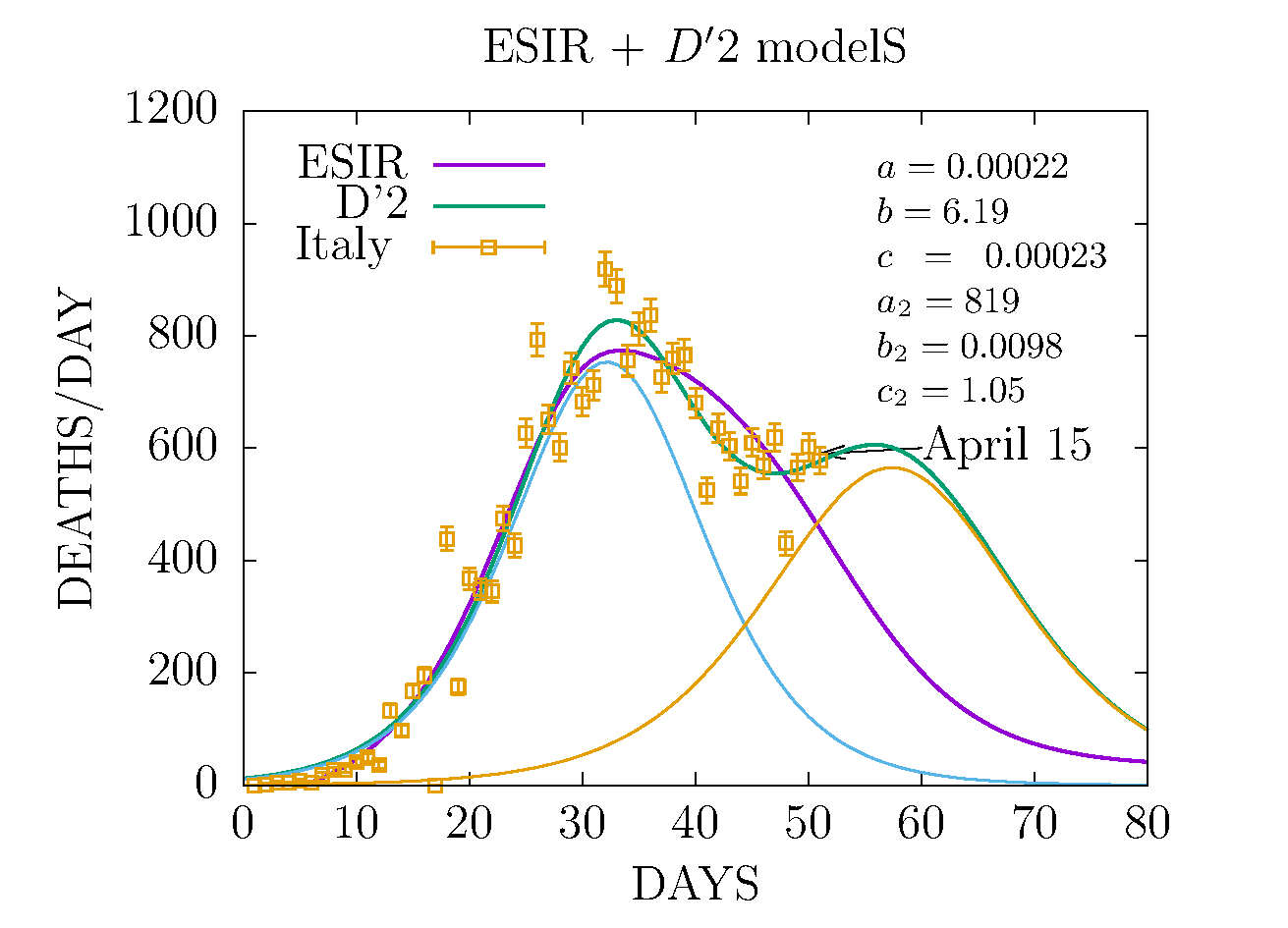
DEATHS PER DAY IN ITALY APRIL 15 - MODELS ESIR AND D'2
-
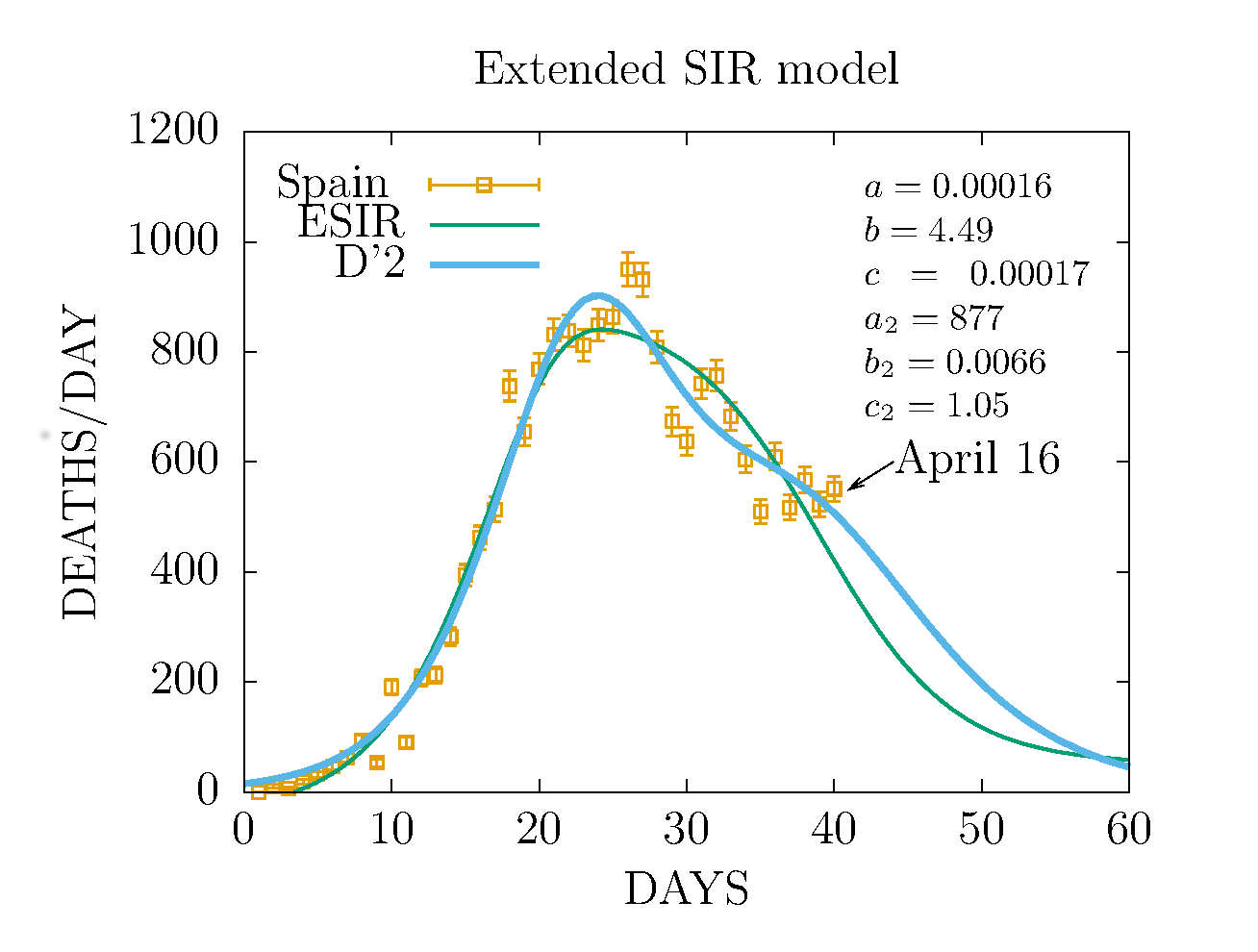
DEATHS PER DAY IN SPAIN APRIL 16 - EXTENDED SIR MODEL VS. D'2 MODEL
WE COMPARE THE NEW EXTENDED SIR MODEL WITH THE D'2 MODEL
THEY GIVE SIMILAR RESULTS
-
DEATHS PER DAY IN SPAIN APRIL 15 - MODEL D'2
-
MODEL D2 DEATHS IN SPAIN 15 APRIL
THE D2 MODEL ASUMES TWO CHANNELS OF INFECTION 1 and 2 with different parameters. Here the fit is made to the total deaths. The data are more compatible with the sum of two D-functions with different parameters.
-
DEATHS PER DAY IN SPAIN APRIL 14 - MODEL D'2
-
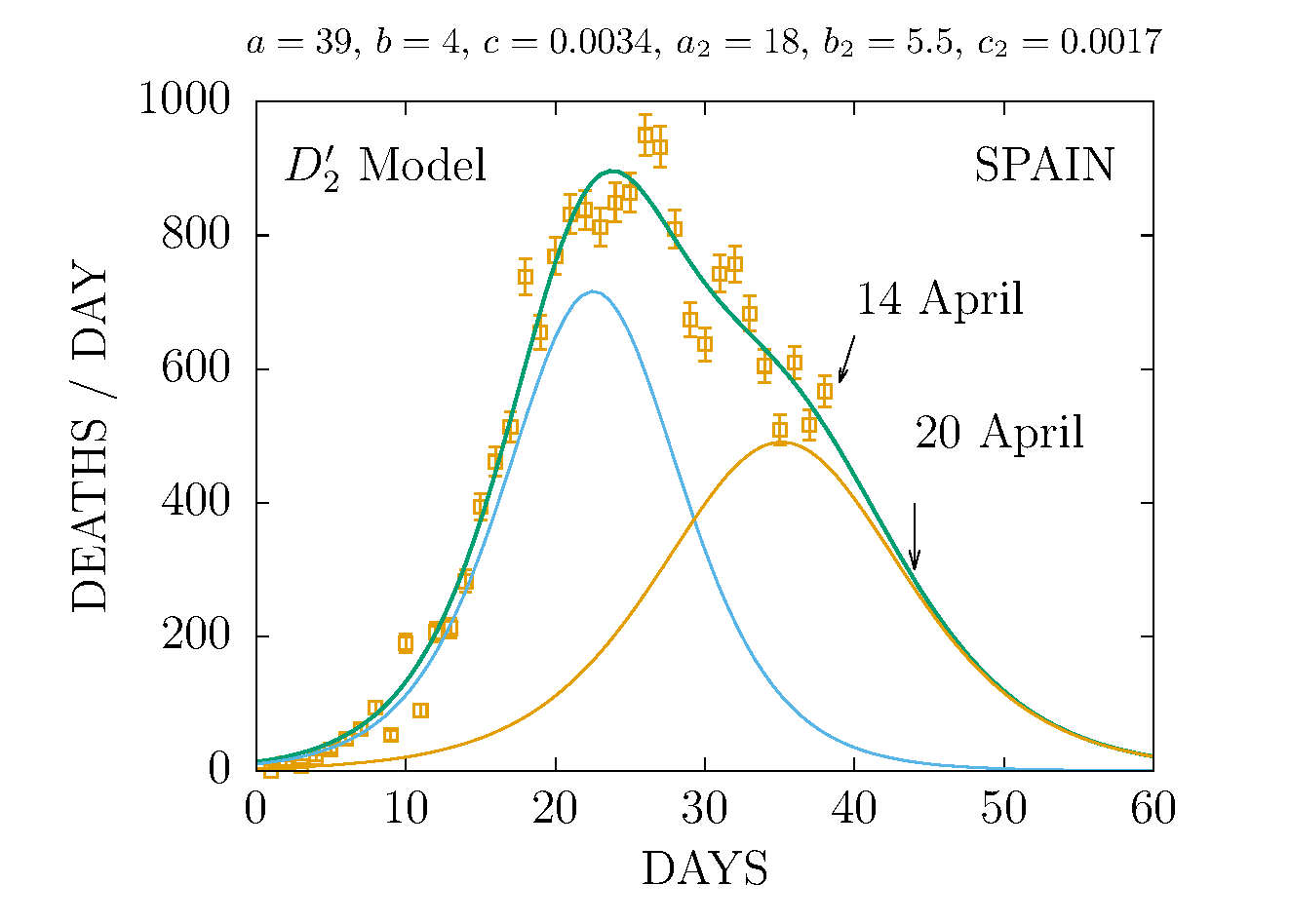
MODEL D2 DEATHS IN SPAIN 14 APRIL
THE D2 MODEL ASUMES TWO CHANNELS OF INFECTION 1 and 2 with different parameters. Here the fit is made to the total deaths. The data are more compatible with the sum of two D-functions with different parameters.
-
DEATHS PER DAY IN SPAIN APRIL 13 - MODEL D'2
-
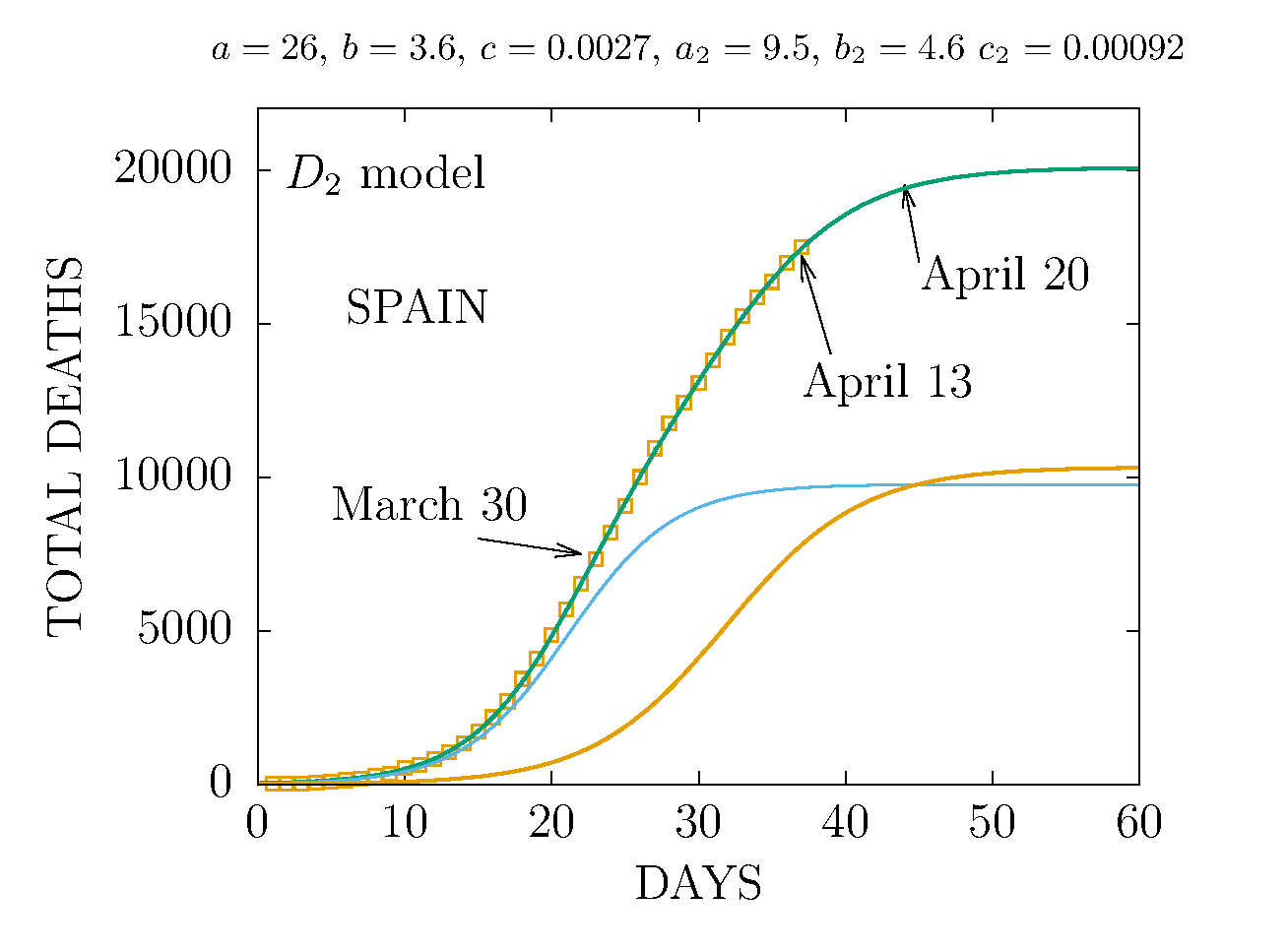
MODEL D2 DEATHS IN SPAIN 13 APRIL
THE D2 MODEL ASUMES TWO CHANNELS OF INFECTION 1 and 2 with different parameters. Here the fit is made to the total deaths. The data are more compatible with the sum of two D-functions with different parameters.
-
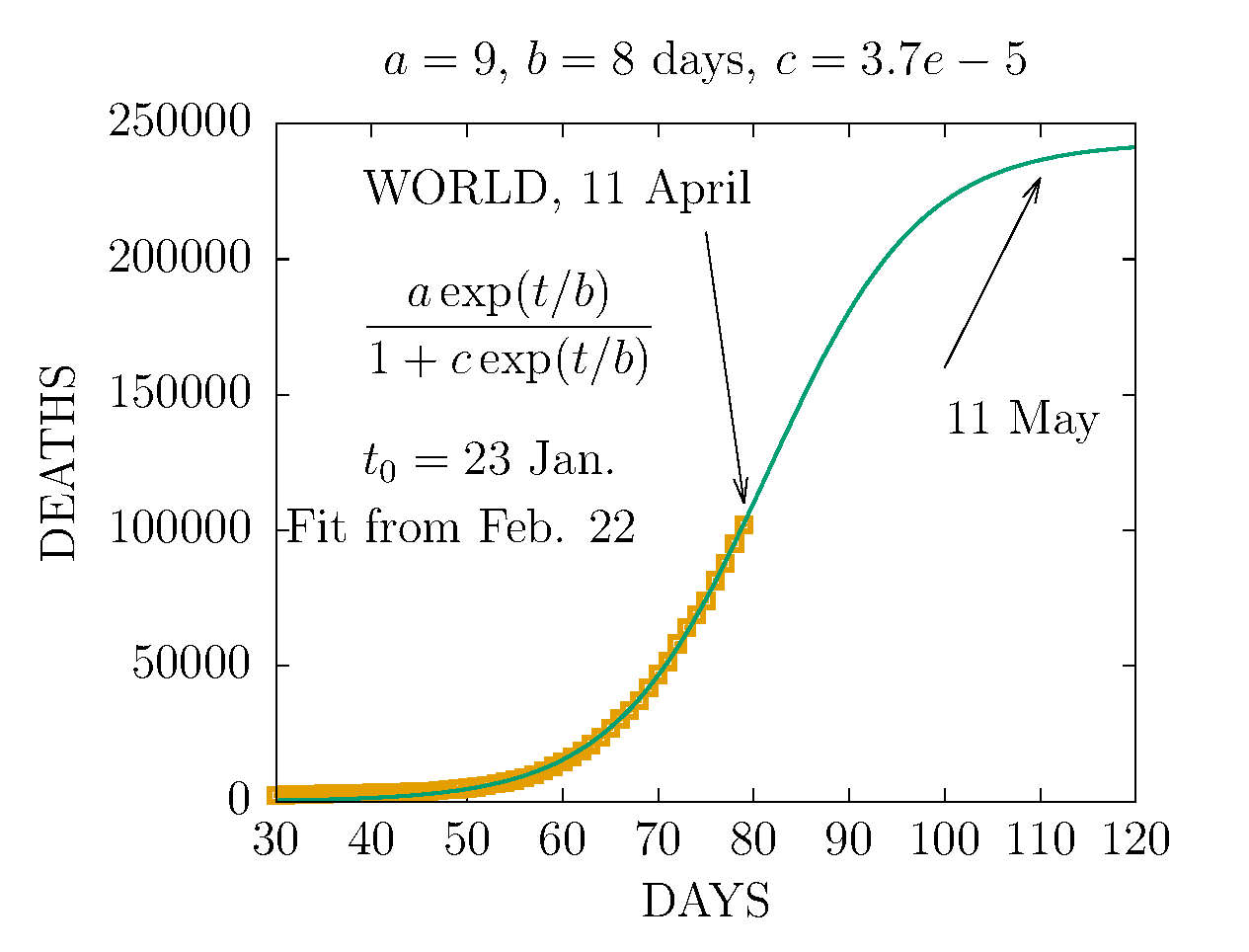
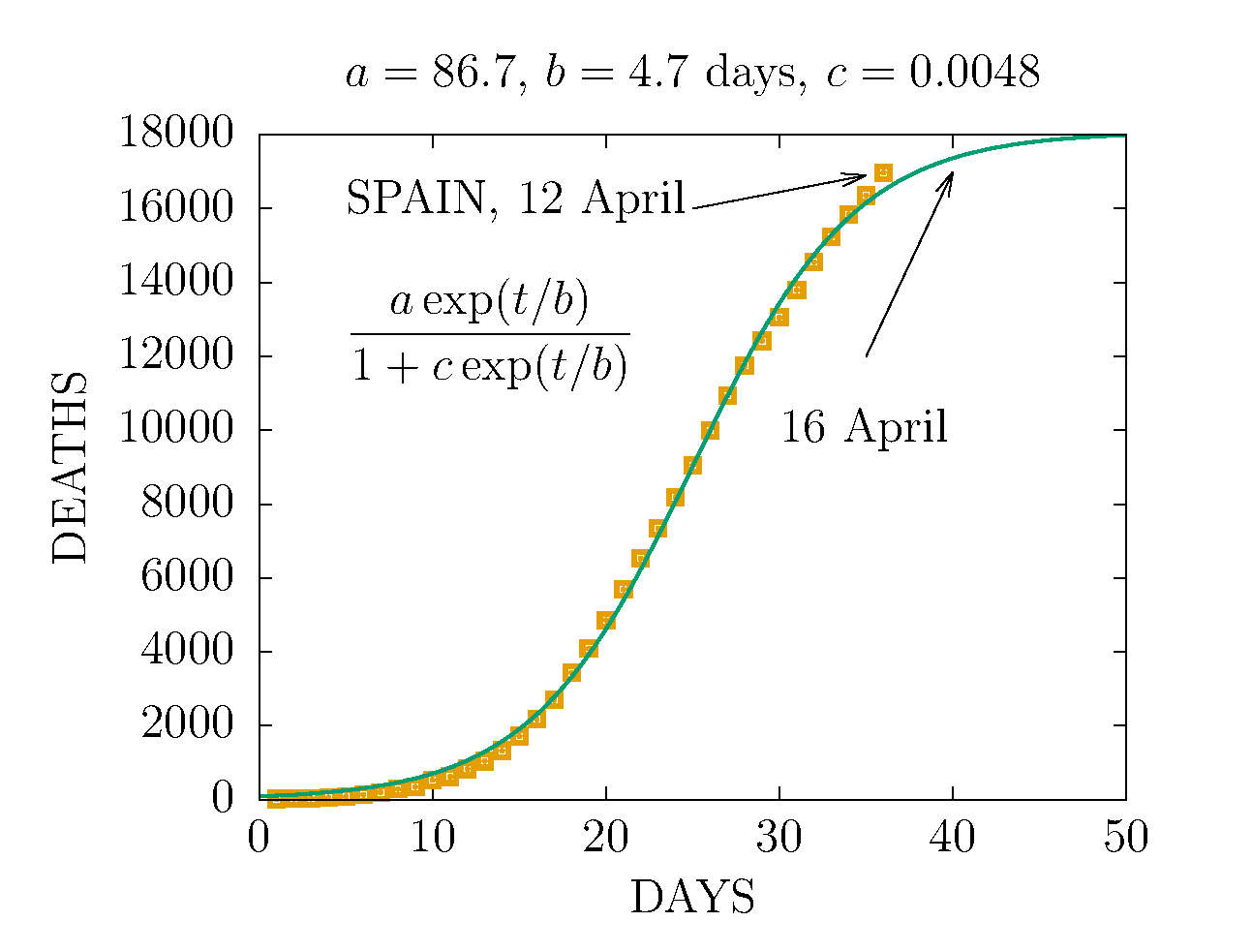
DEATHS IN THE WORLD 12 APRIL
-
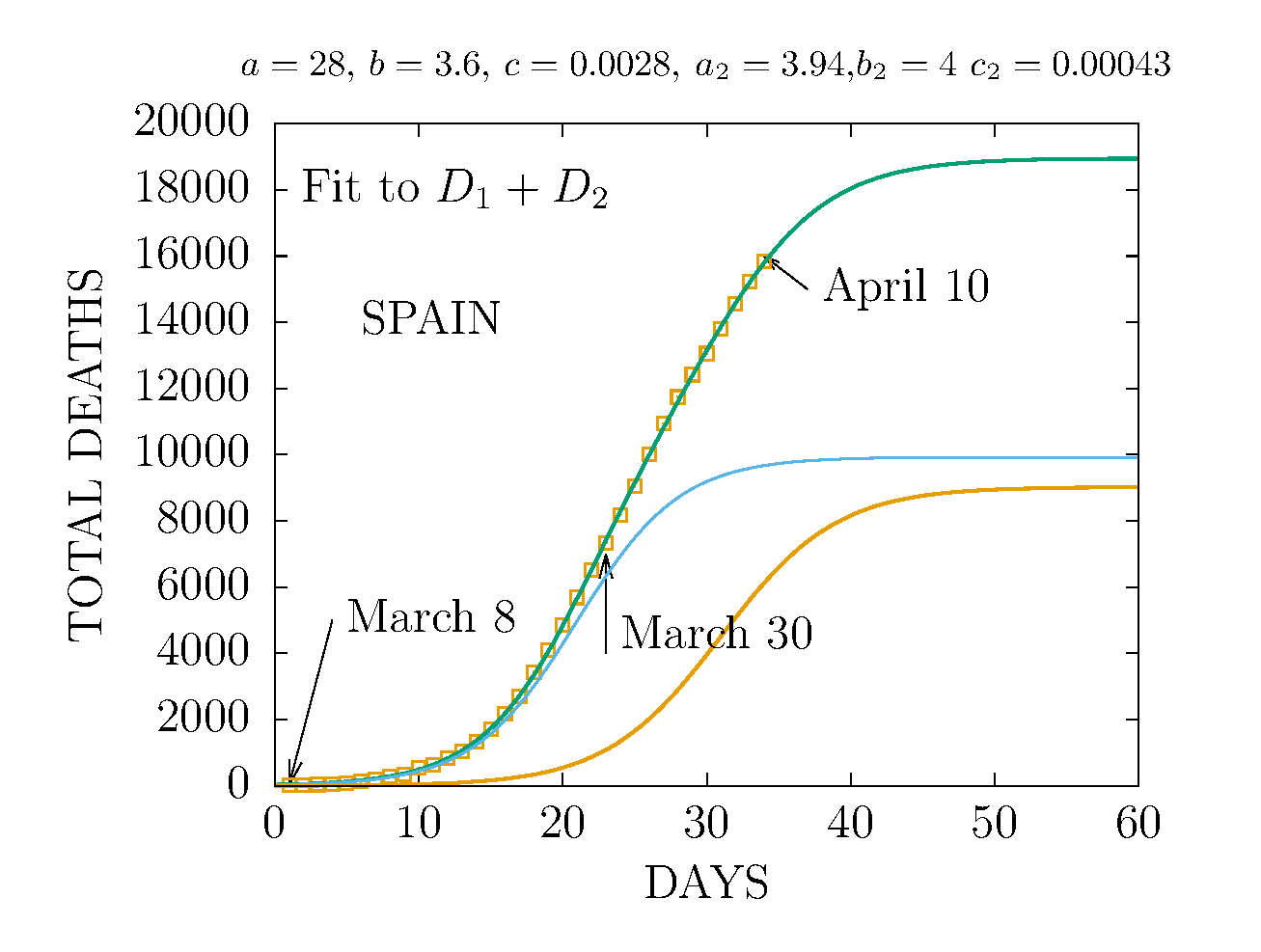
MODEL D2 DEATHS IN SPAIN 12 APRIL
THE D2 MODEL ASUMES TWO CHANNELS OF INFECTION 1 and 2 with different parameters. Here the fit is made to the total deaths. The data are more compatible with the sum of two D-functions with different parameters.
-
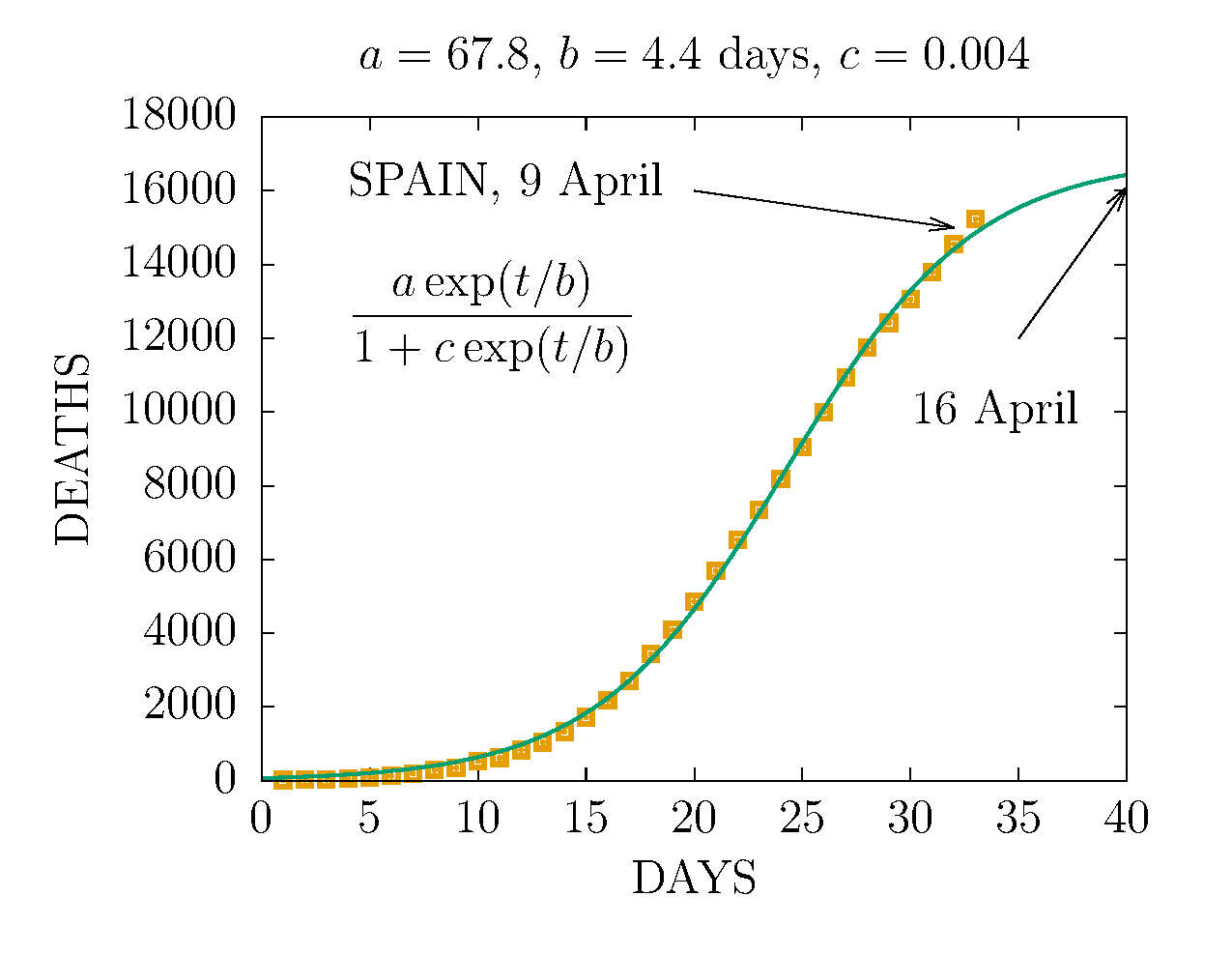
DEATHS IN SPAIN 12 APRIL (DAY 37TH)
-
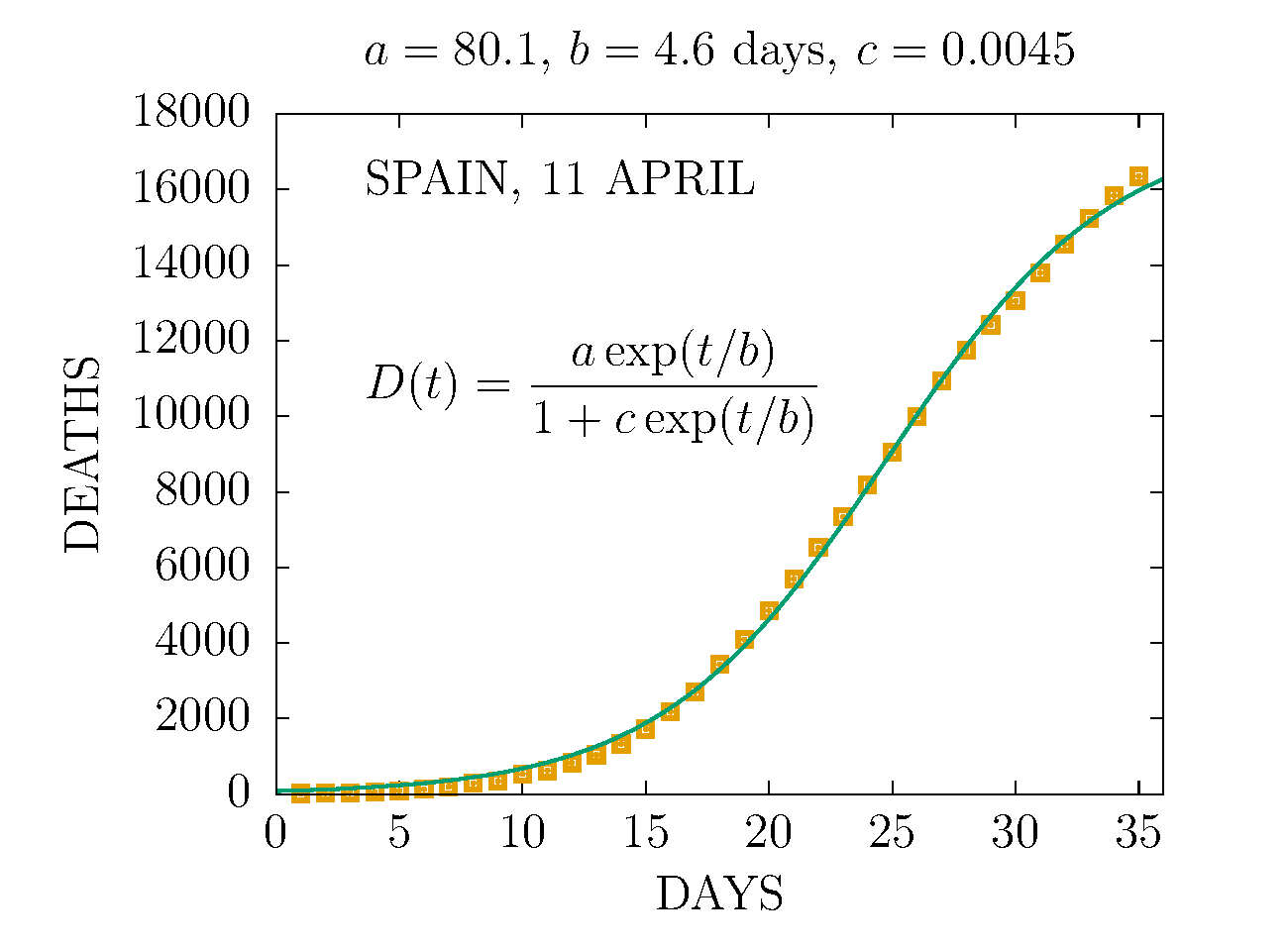
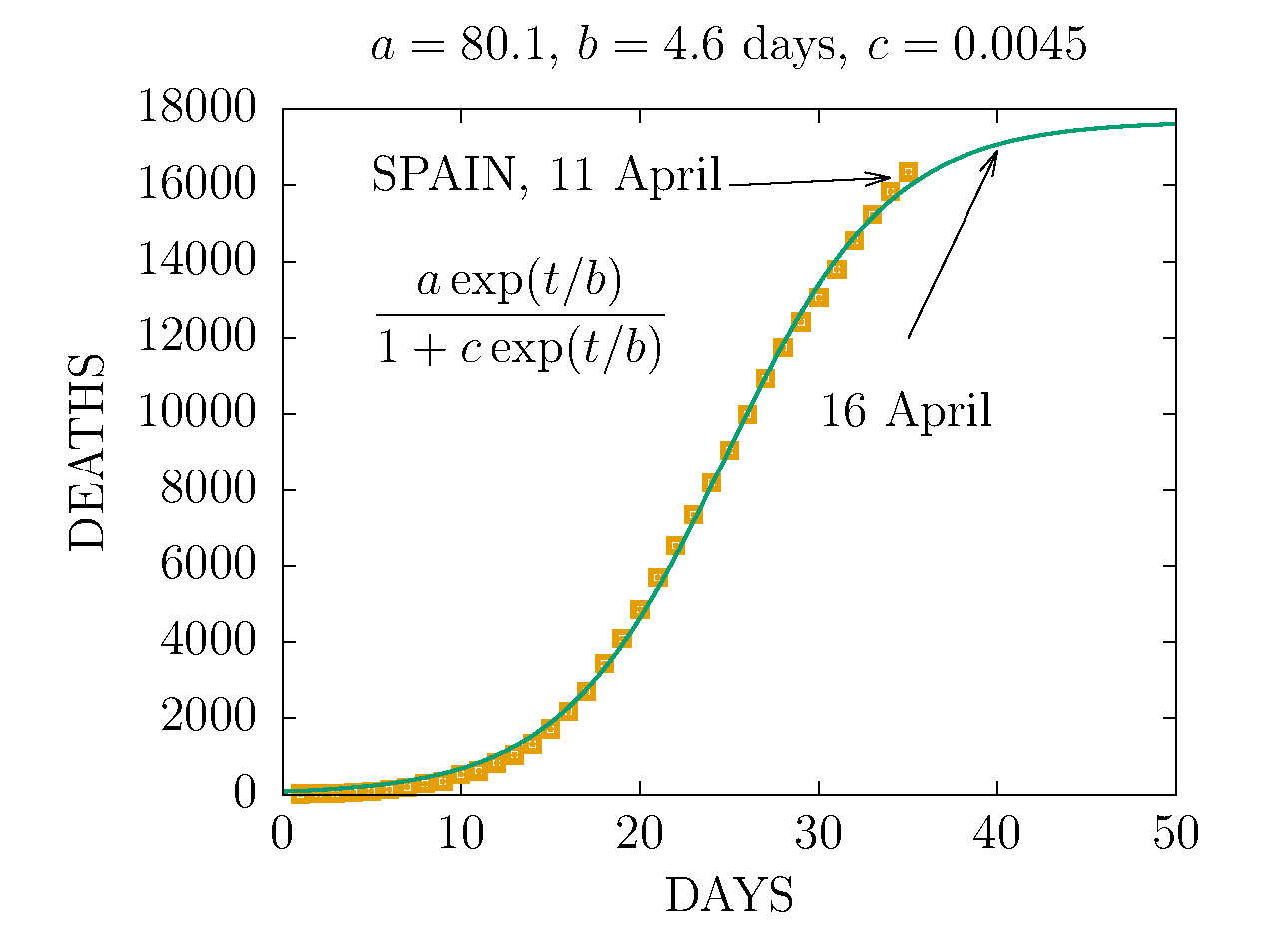
MODEL D2 DEATHS IN SPAIN 11 APRIL
THE D2 MODEL ASUMES TWO CHANNELS OF INFECTION 1 and 2 with different parameters. Here the fit is made to the total deaths. The data are more compatible with the sum of two D-functions with different parameters.
-
DEATHS PER DAY IN SPAIN 11 APRIL
-
DEATHS IN SPAIN 11 APRIL (DAY 36TH)
-
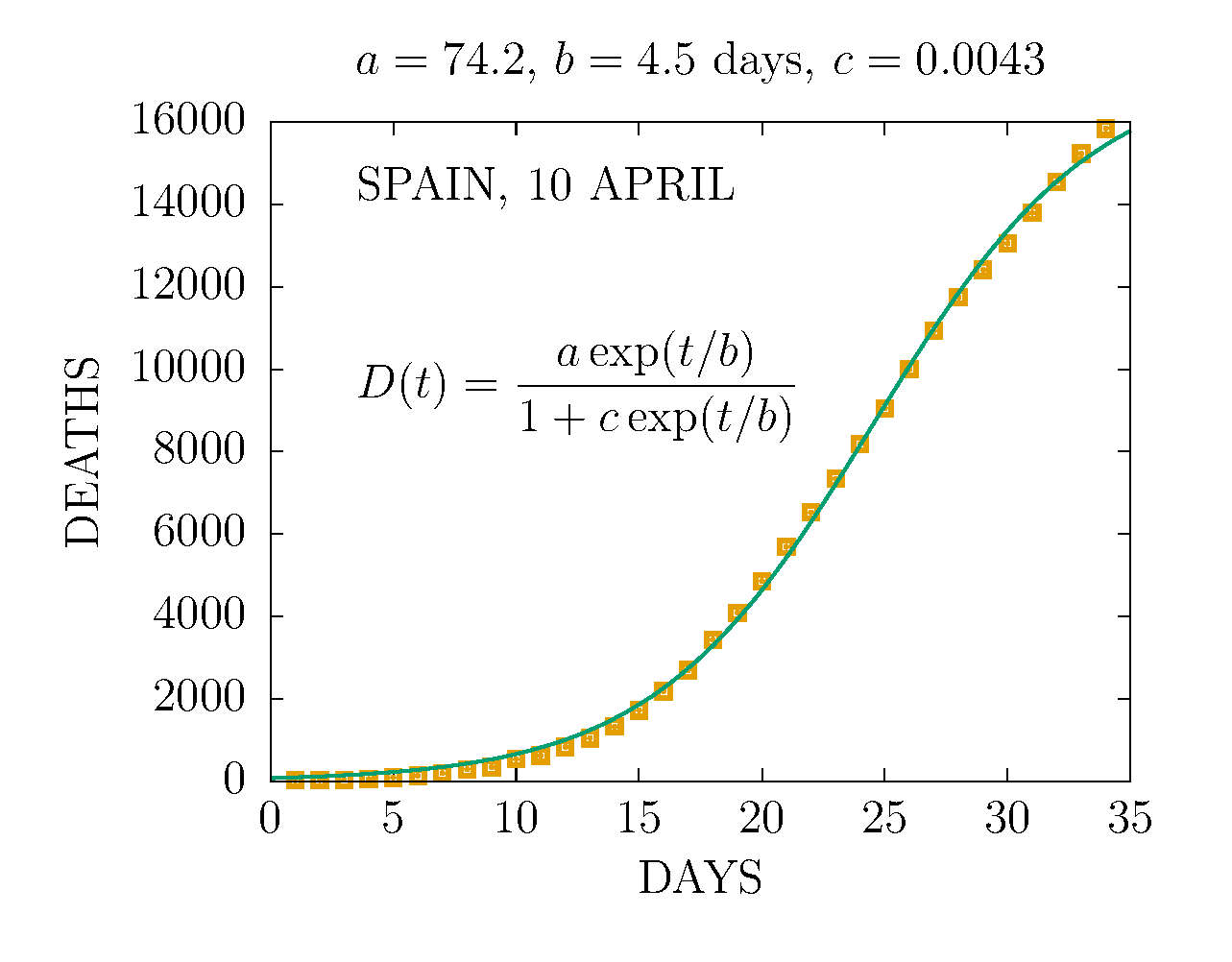
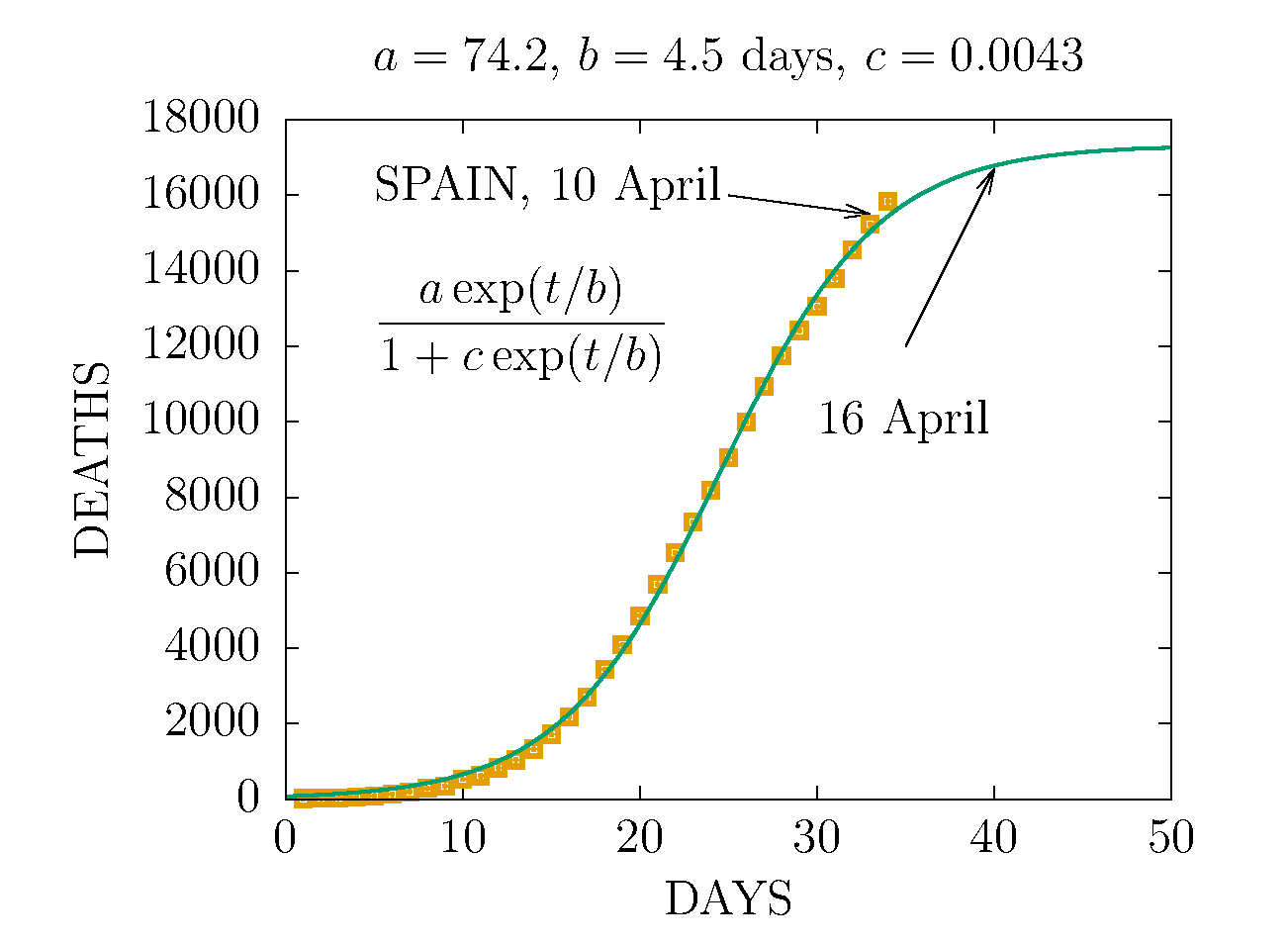
MODEL D2 DEATHS IN SPAIN 10 APRIL
THE D2 MODEL ASUMES TWO CHANNELS OF INFECTION 1 and 2 with different parameters. Here the fit is made to the total deaths. The data are more compatible with the sum of two D-functions with different parameters. This is the worst scenario we can predict with this data.
-
DEATHS PER DAY IN SPAIN 10 APRIL
-
DEATHS IN SPAIN 10 APRIL (DAY 35TH)
-
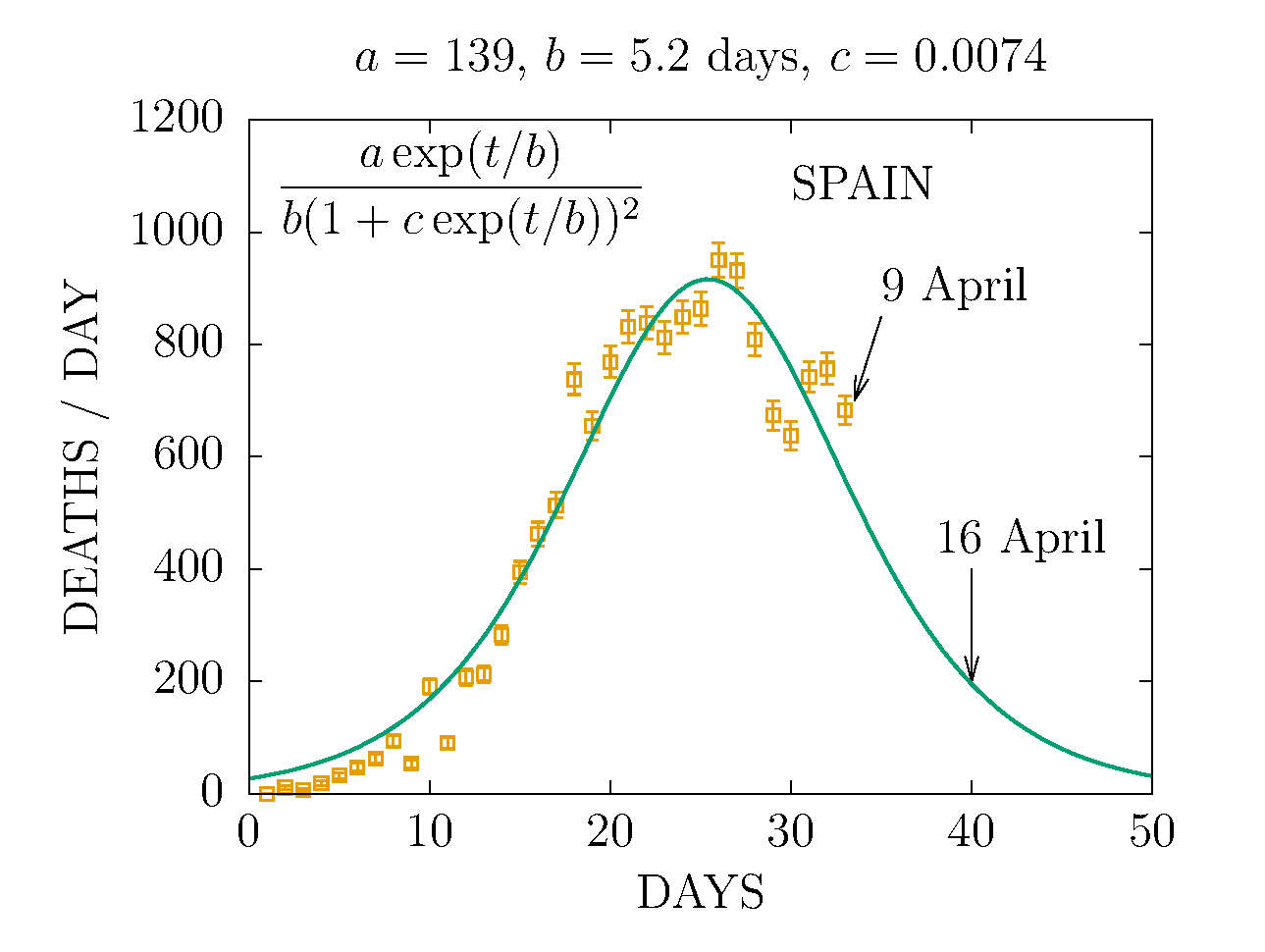
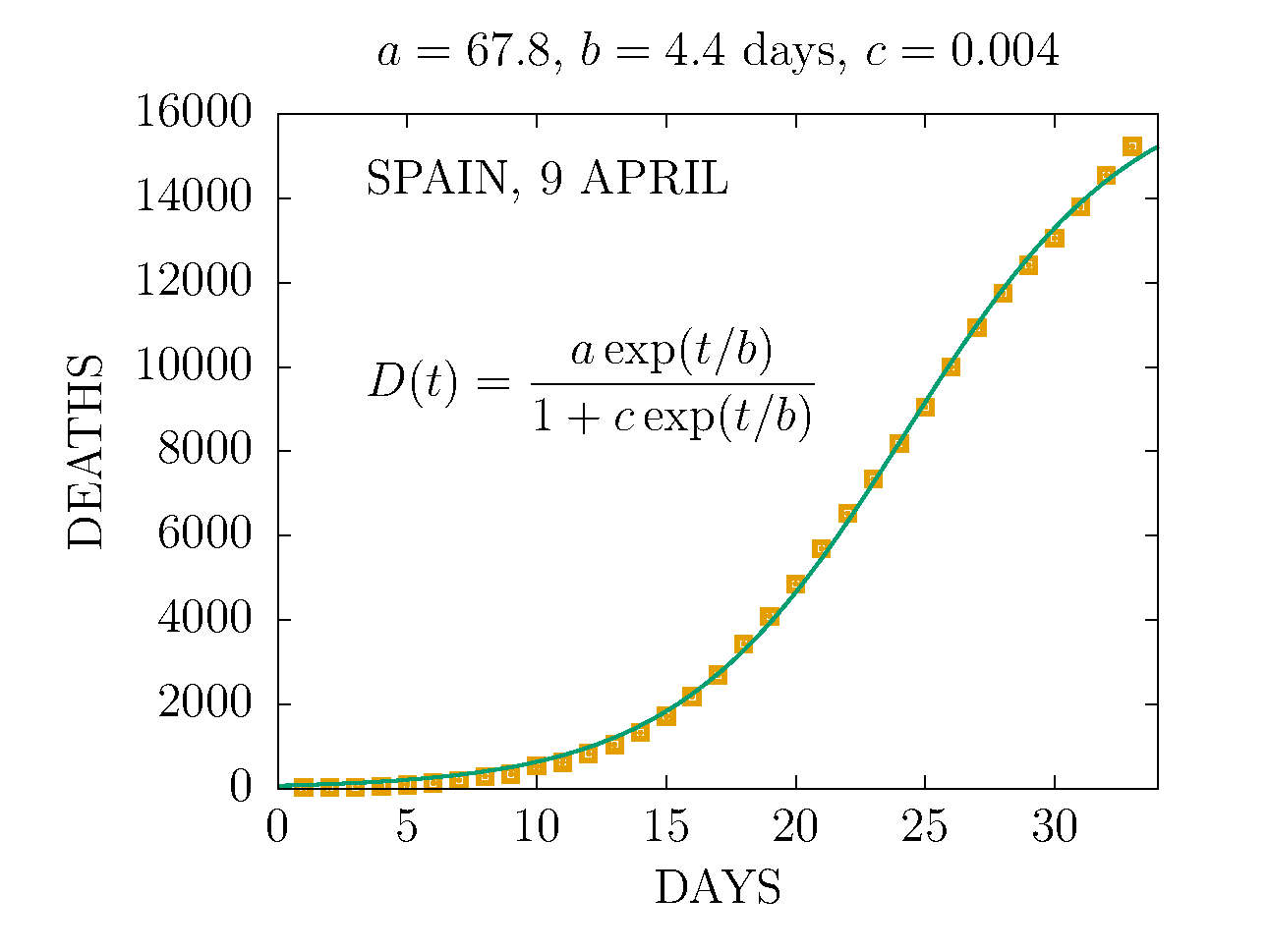
MODEL D2 DEATHS IN SPAIN 9 APRIL
THE D2 MODEL ASUMES TWO CHANNELS OF INFECTION 1 and 2 with different parameters. Here the fit is made to de deaths per day. The data are more compatible with the sum of two D-functions with different parameters. This is the worst scenario we can predict with this data.
-
DEATHS PER DAY IN SPAIN 9 APRIL
-
DEATHS IN SPAIN 9 APRIL (DAY 33TH)
-
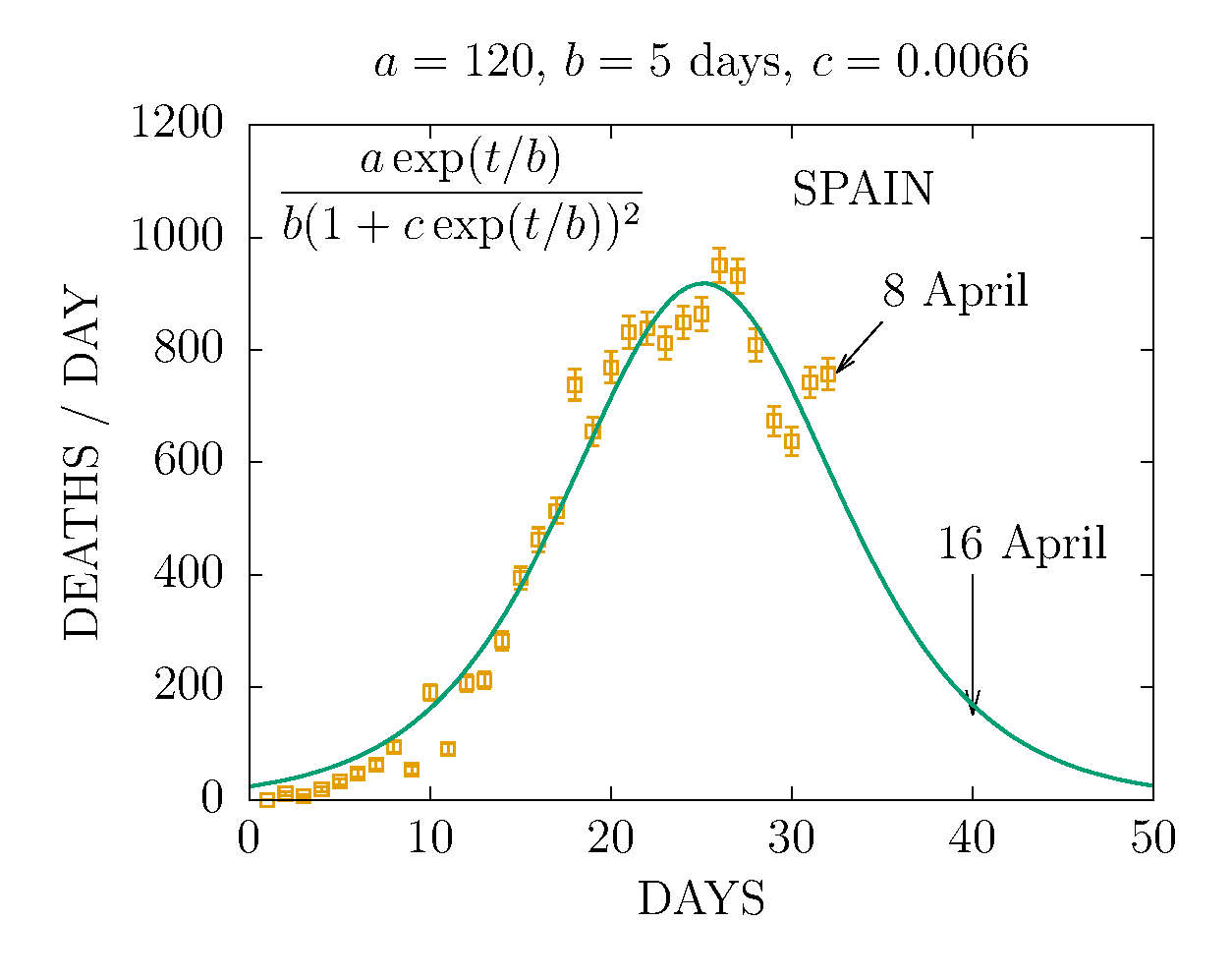
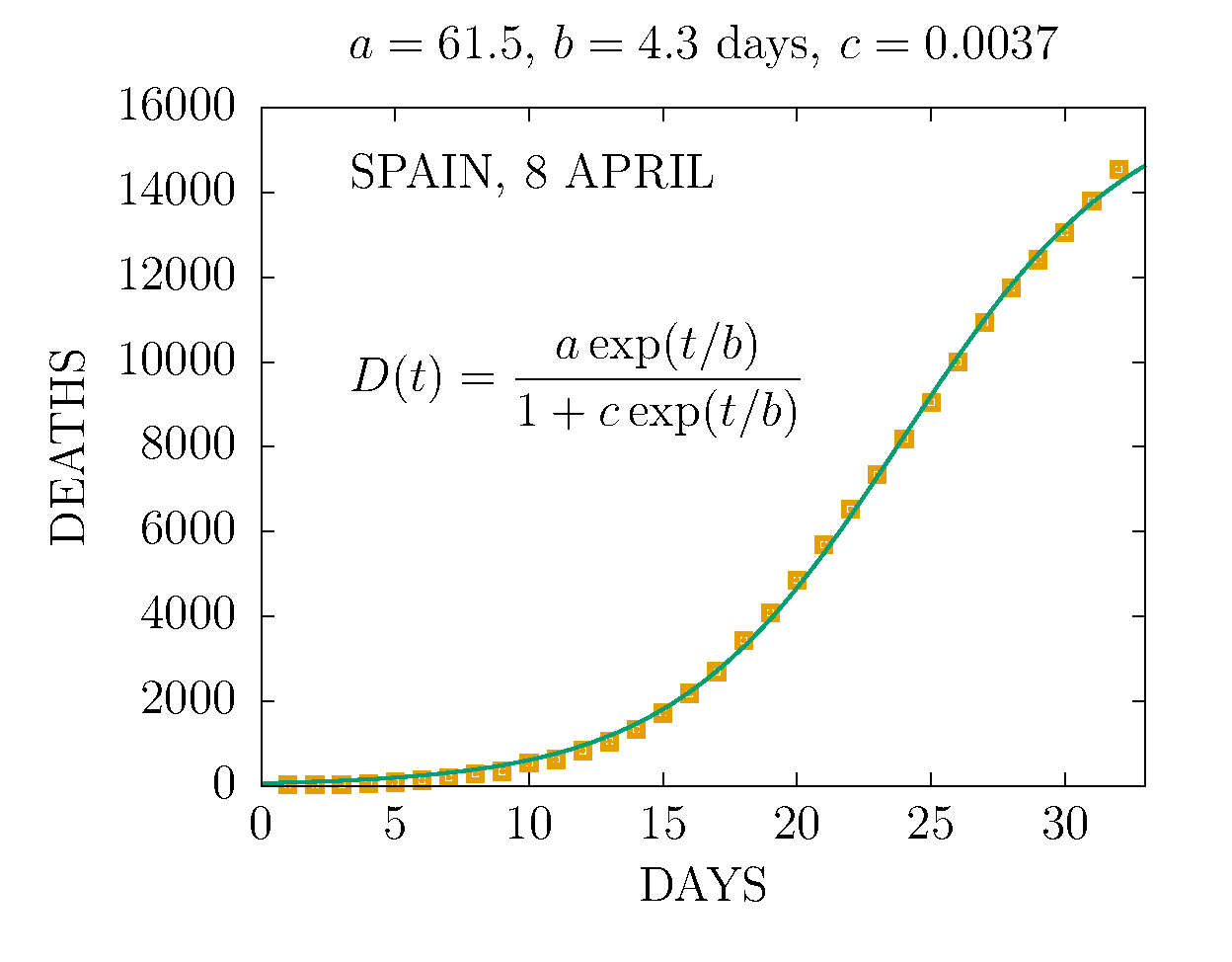
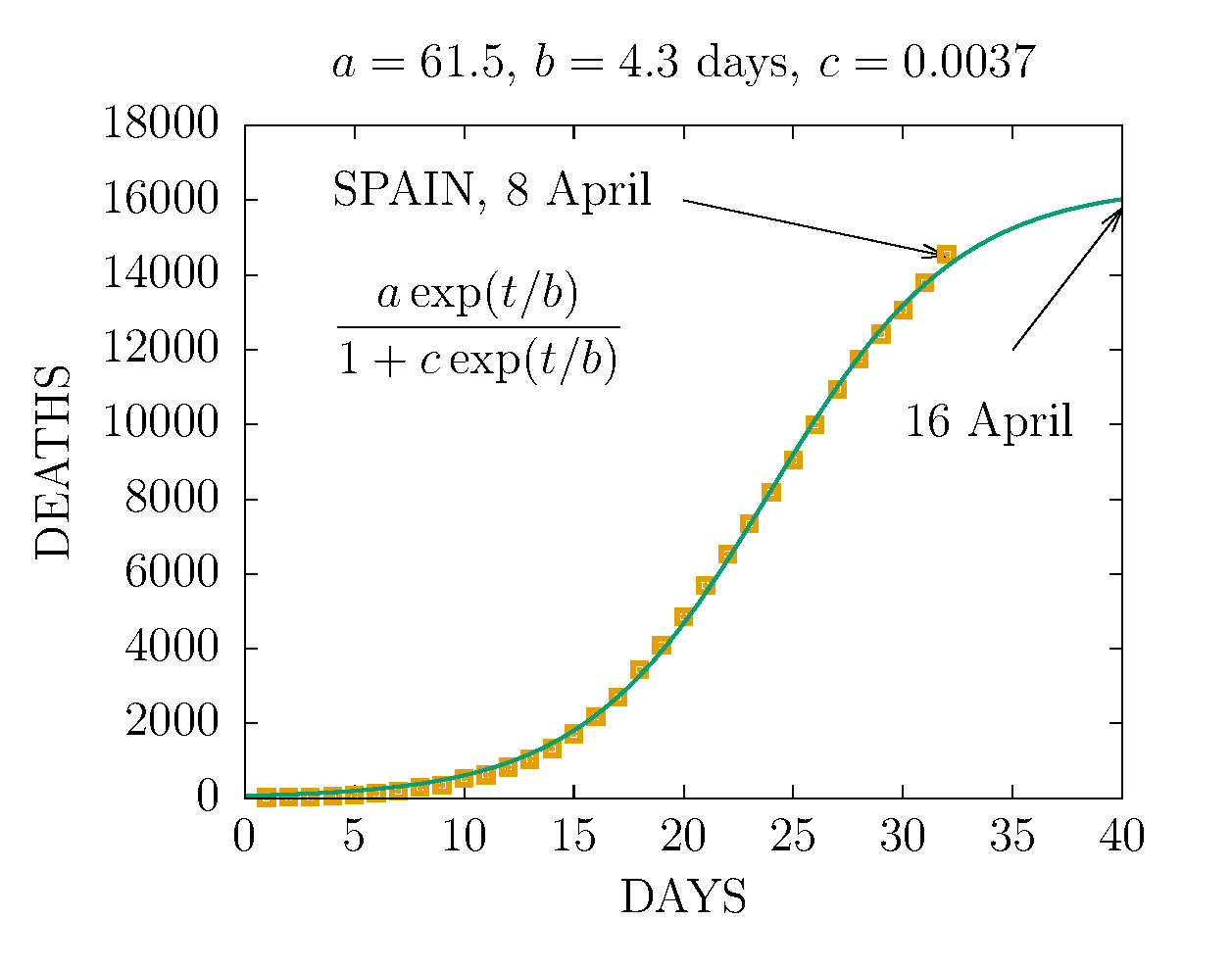
DEATHS PER DAY IN SPAIN 8 APRIL
-
DEATHS IN SPAIN 8 APRIL (DAY 32TH)
-
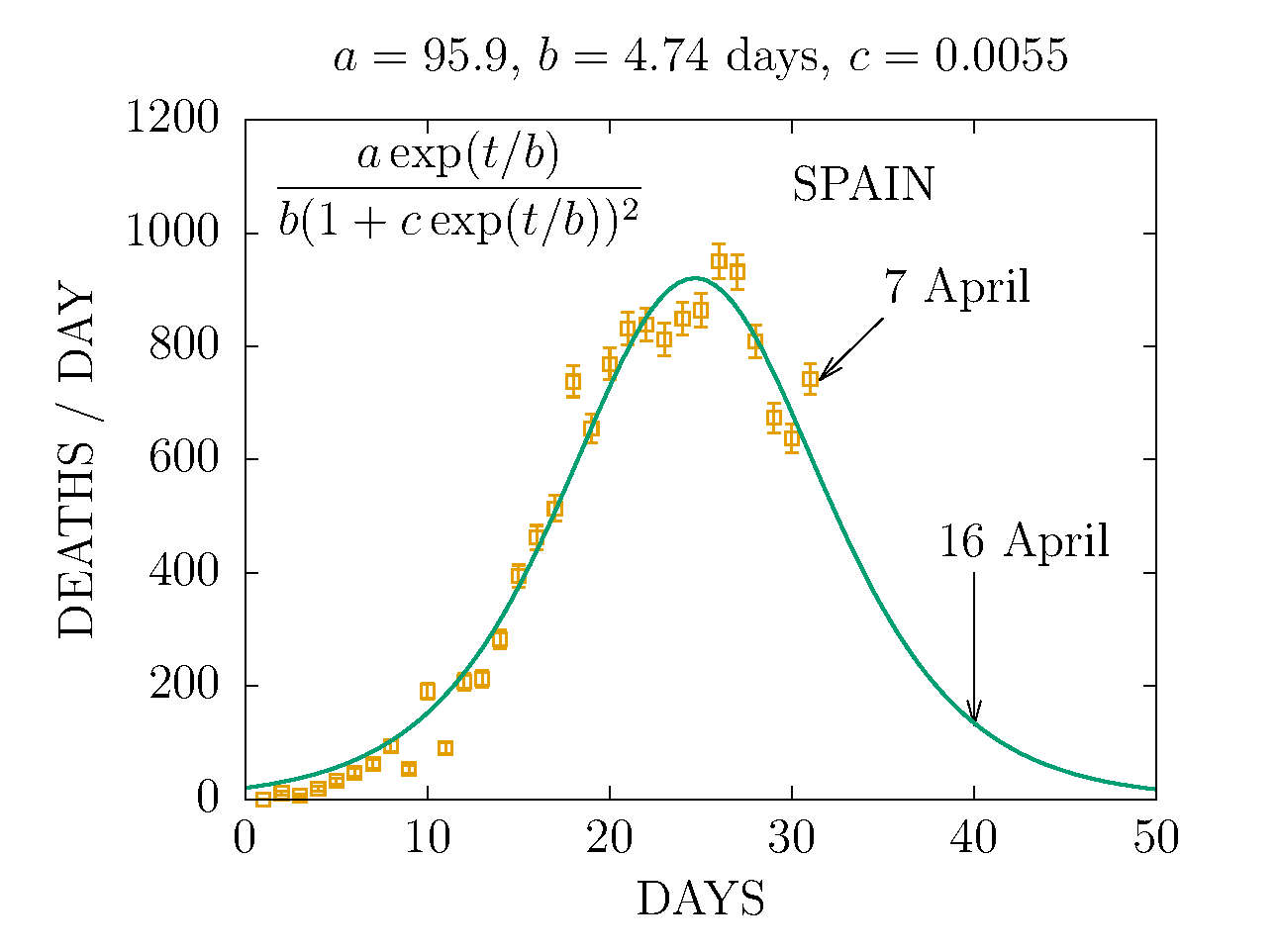
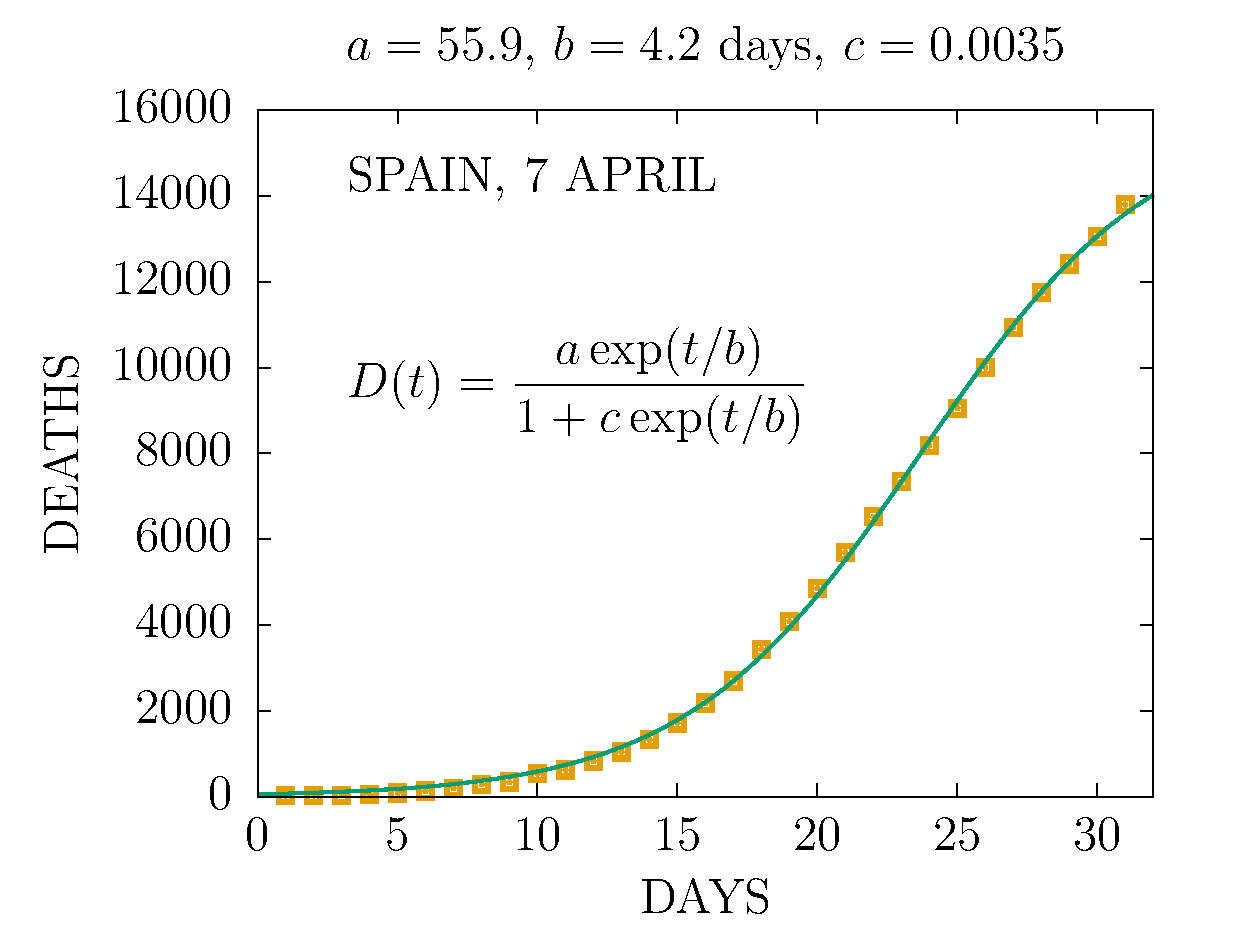
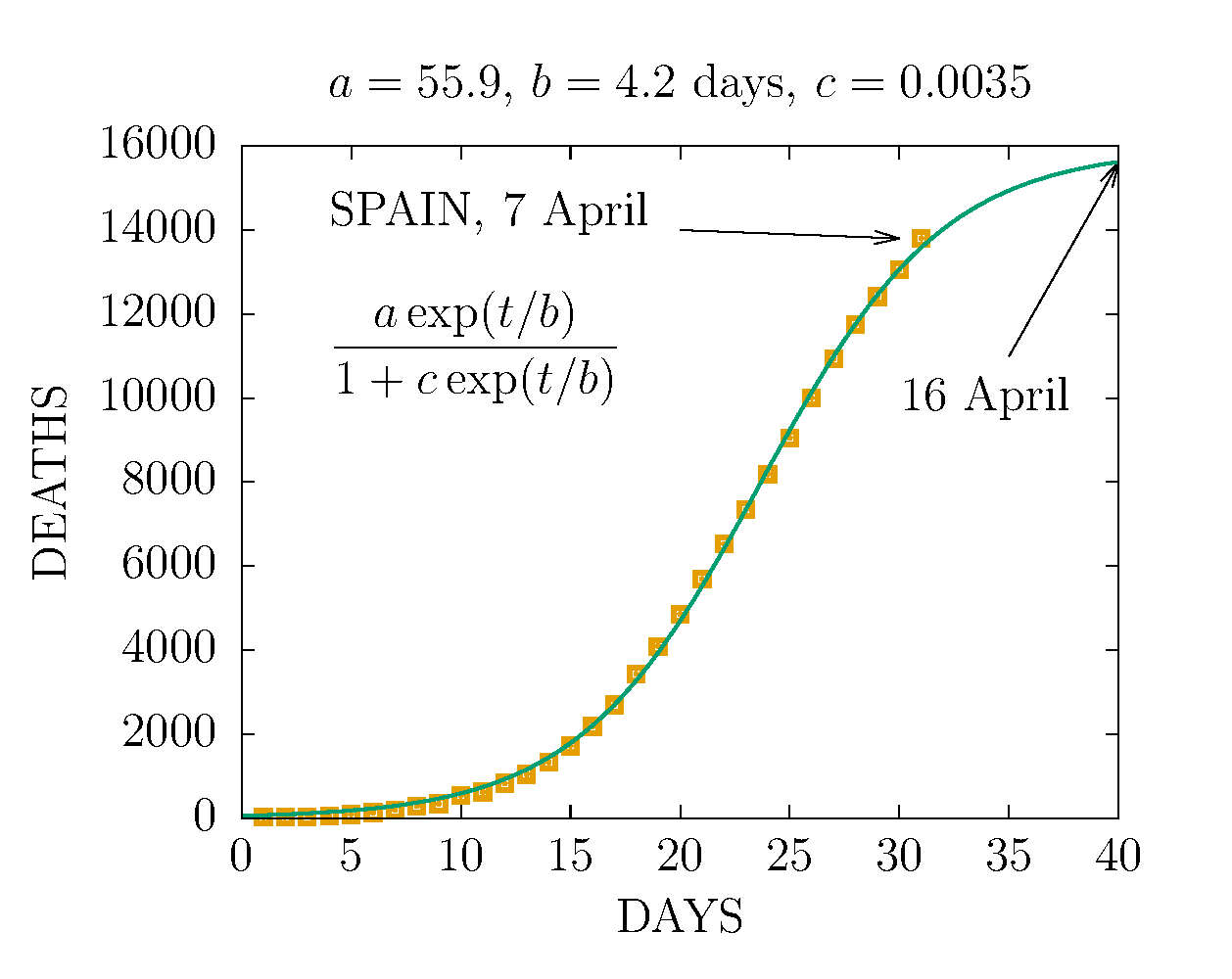
DEATHS PER DAY IN SPAIN 7 APRIL
-
DEATHS IN SPAIN 7 APRIL (DAY 31TH)
-
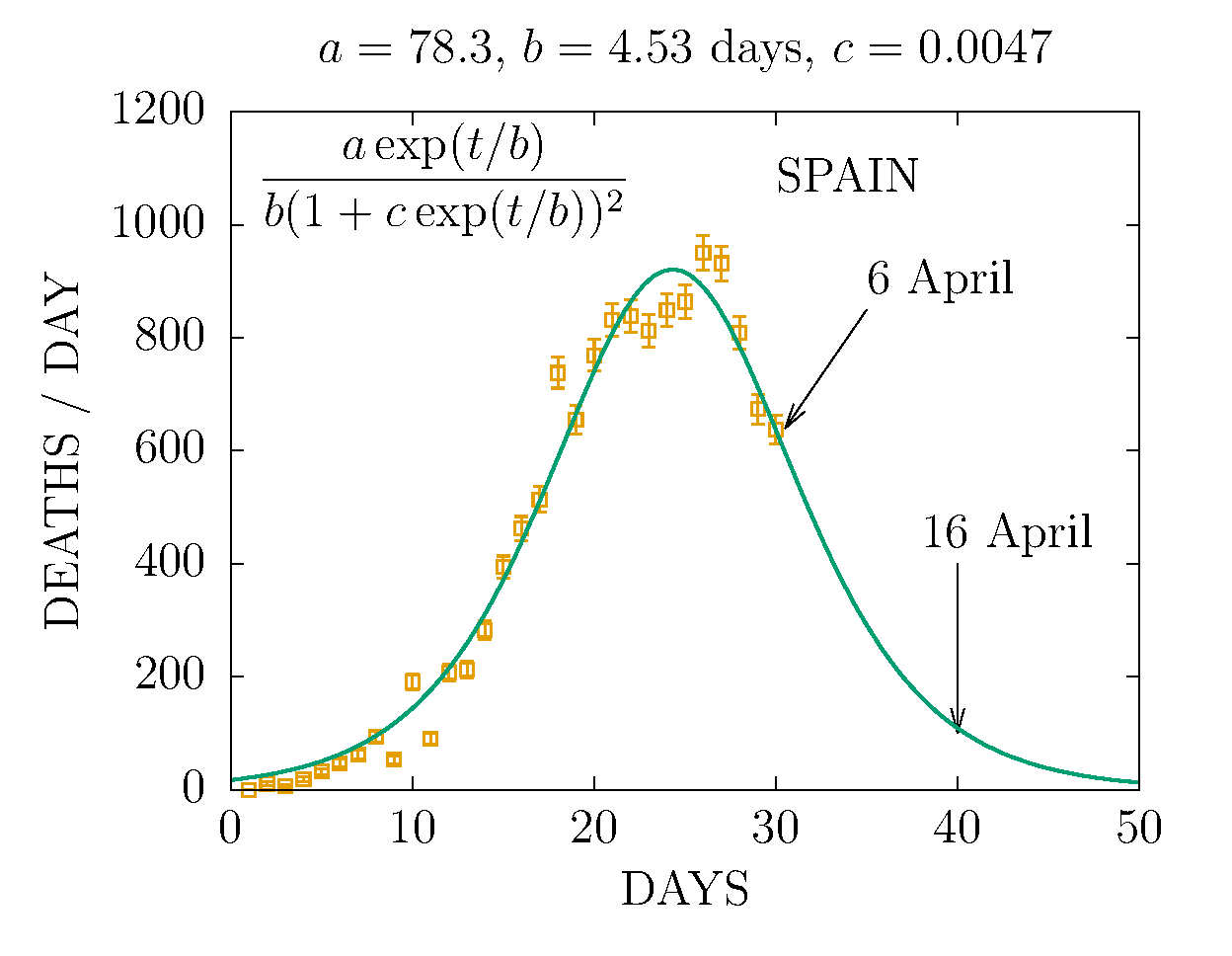
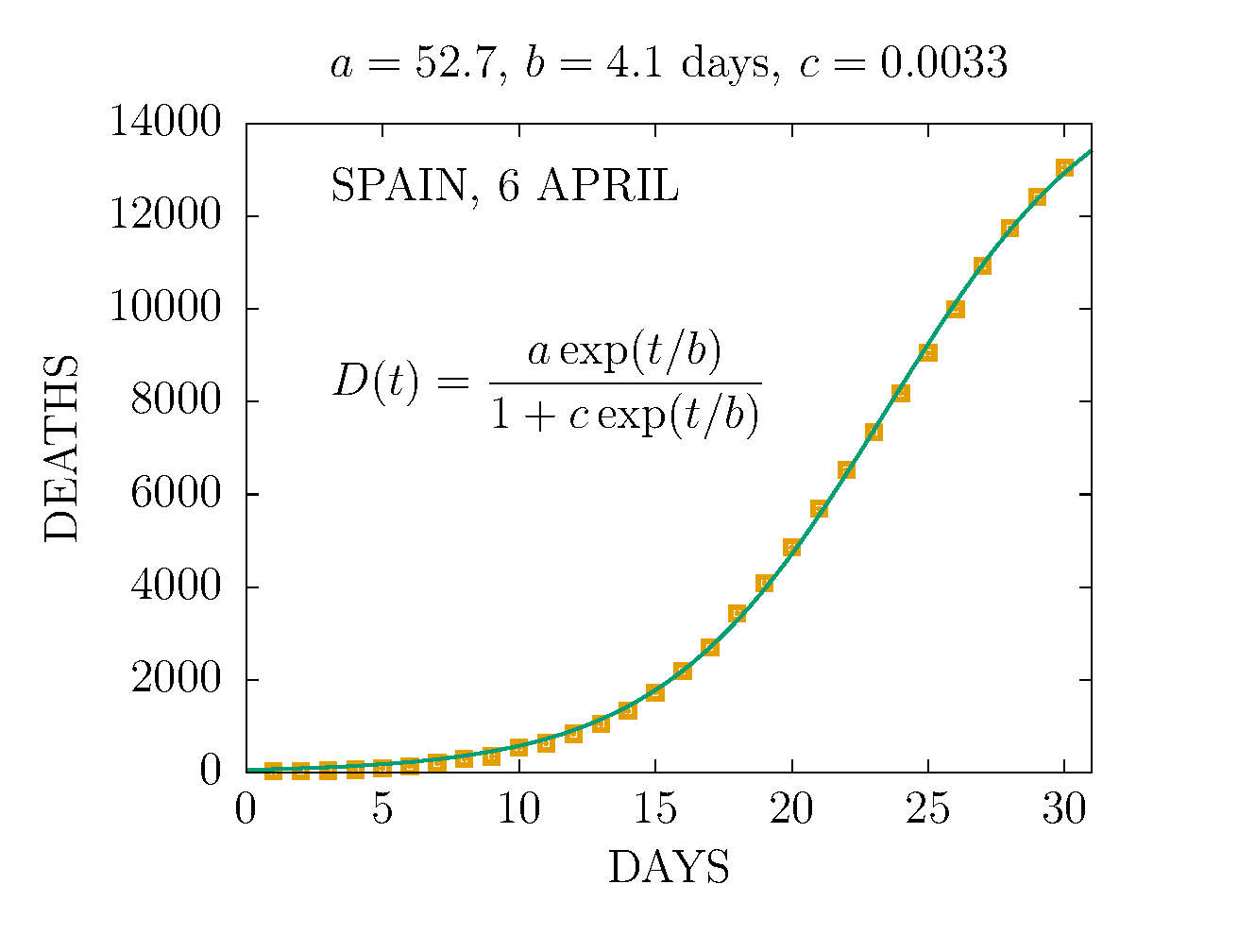
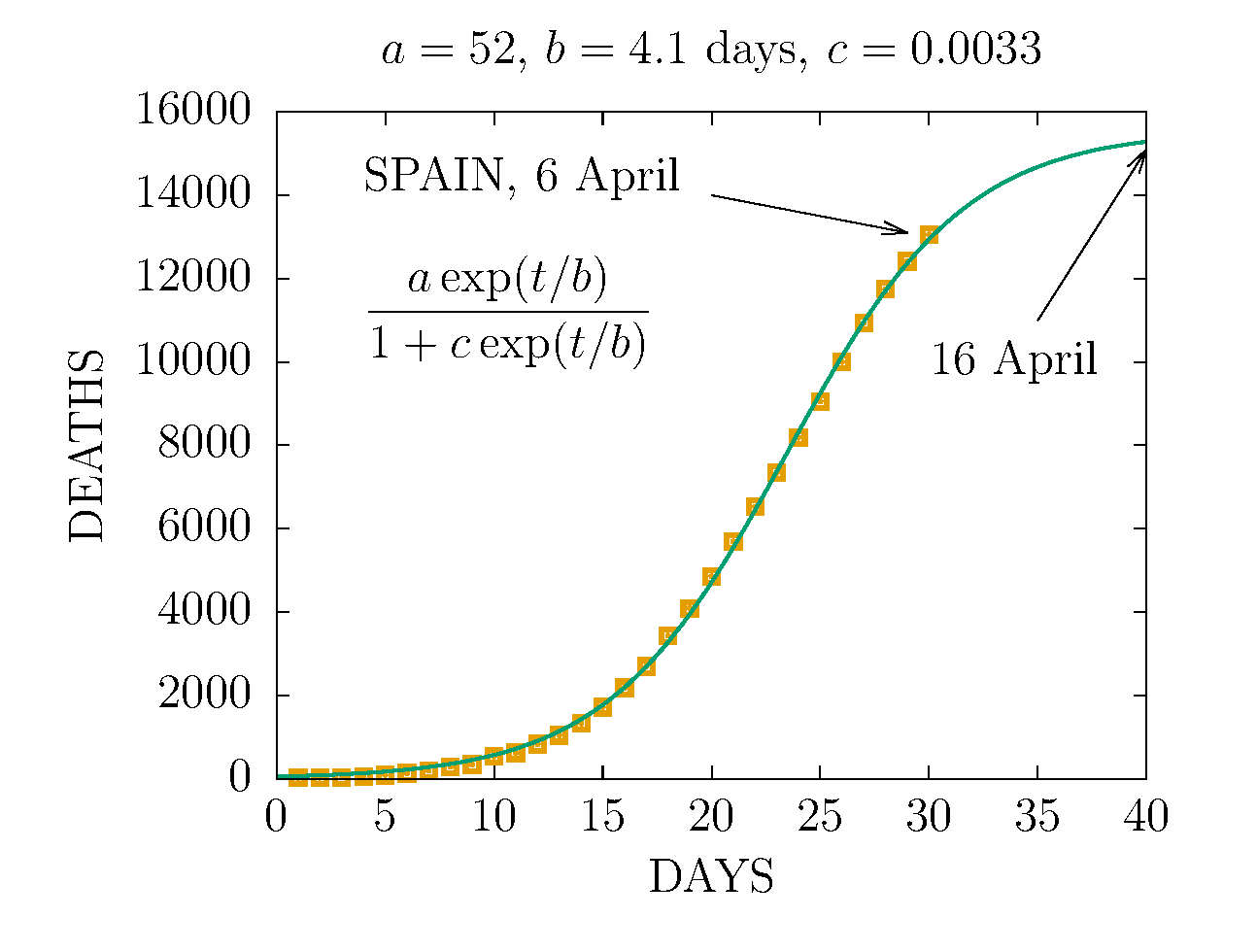
DEATHS PER DAY IN SPAIN 6 APRIL
-
DEATHS IN SPAIN 6 APRIL (DAY 30TH)
-
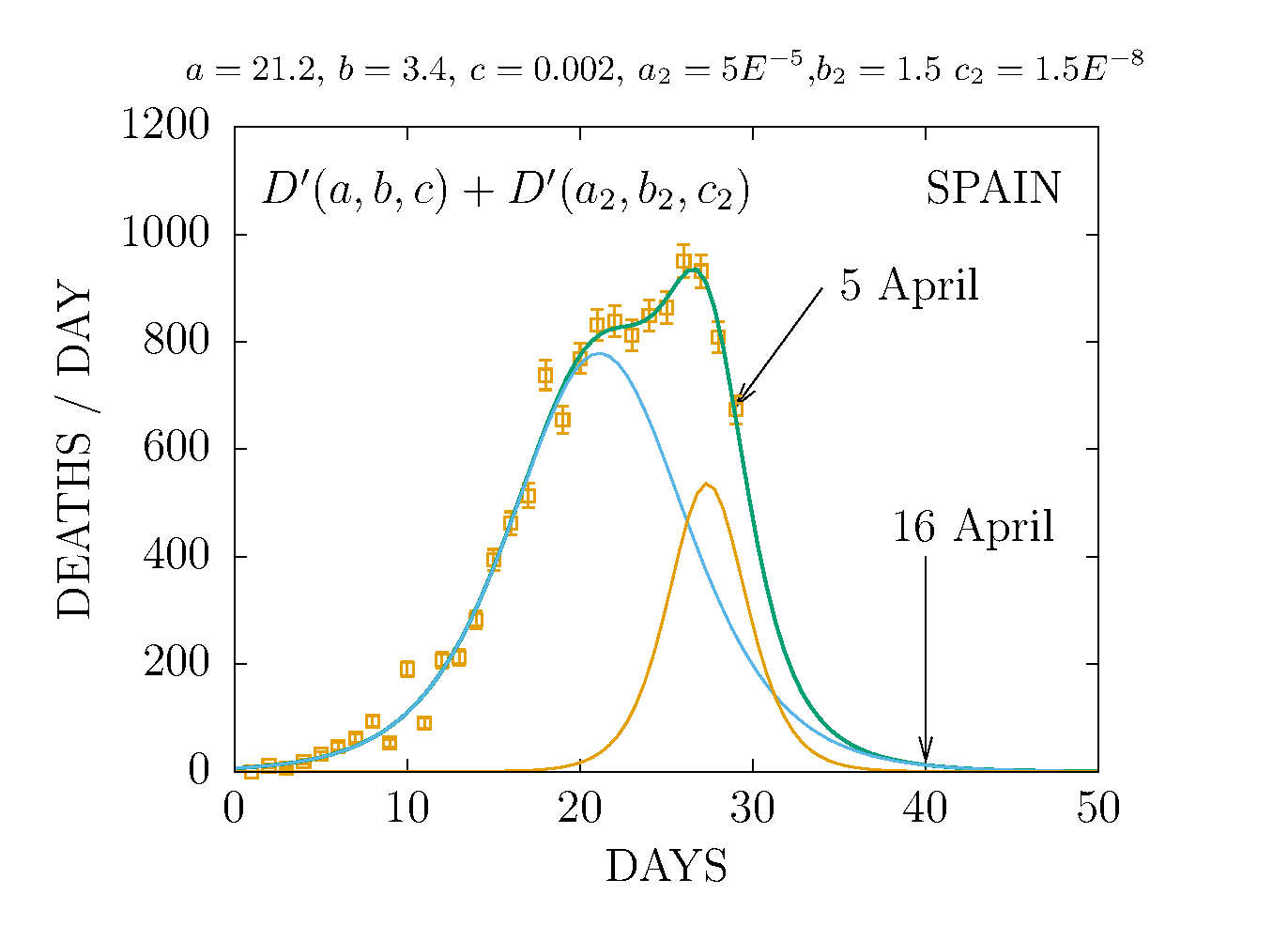
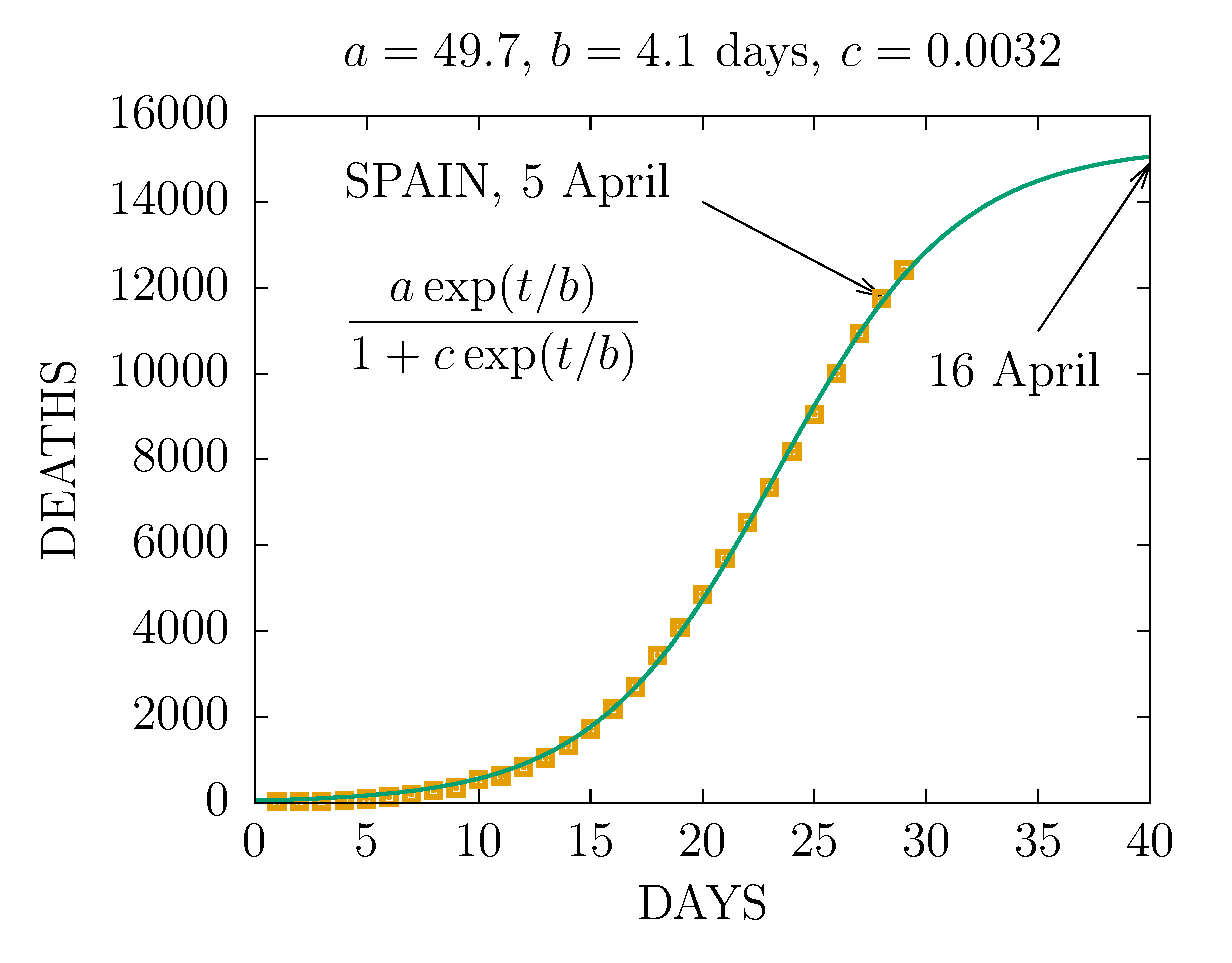
MODEL D' WITH TWO CHANNELS - SPAIN 5 APRIL (DAY 28TH)
-
DEATHS PER DAY IN SPAIN 5 APRIL
-
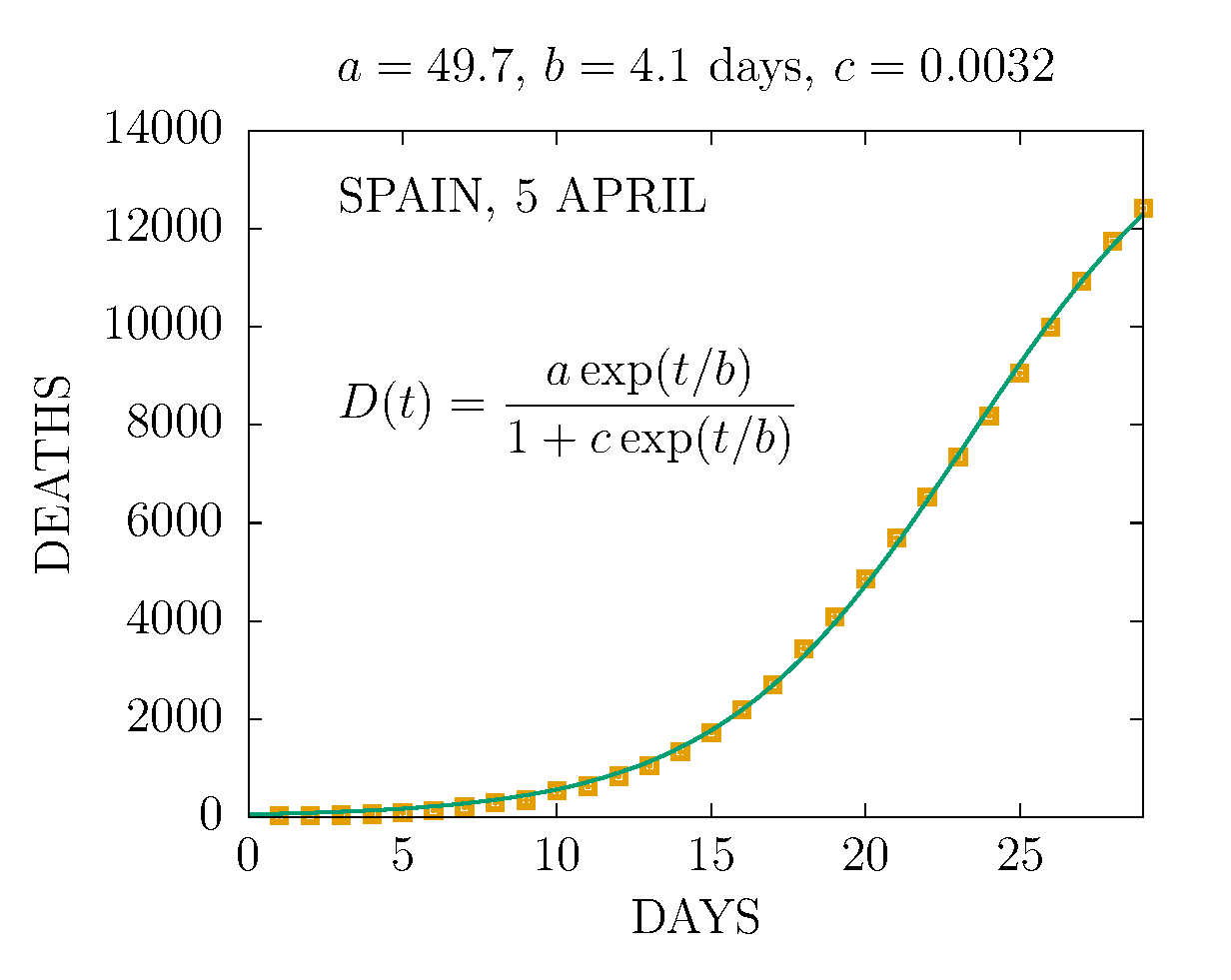
DEATHS IN SPAIN 5 APRIL (DAY 28TH)
-
DEATHS PER DAY IN SPAIN 4 APRIL
-
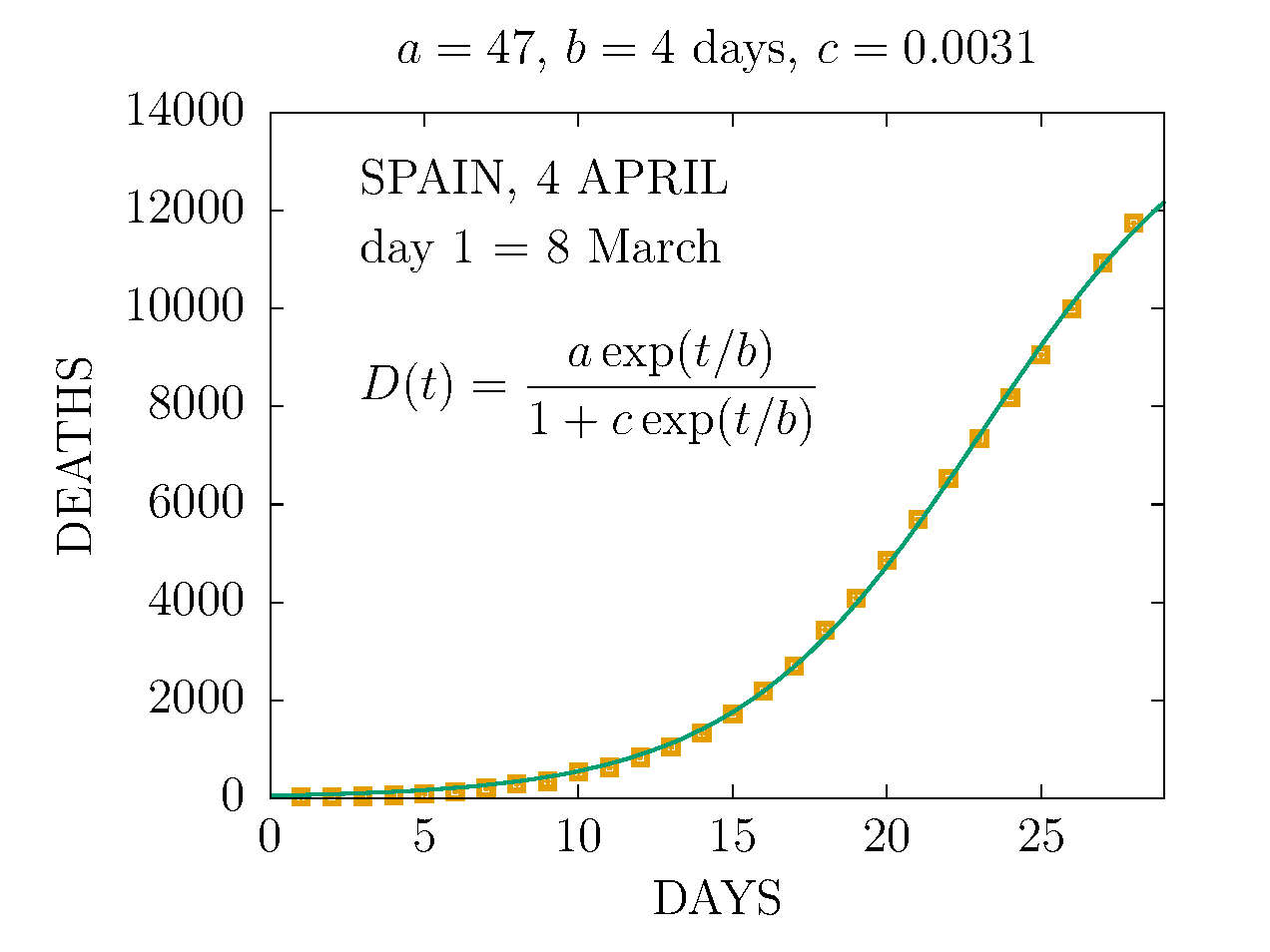
DEATHS IN SPAIN 4 APRIL (DAY 27TH)
-
MODEL D'2 DEATHS PER DAY IN SPAIN 3 APRIL
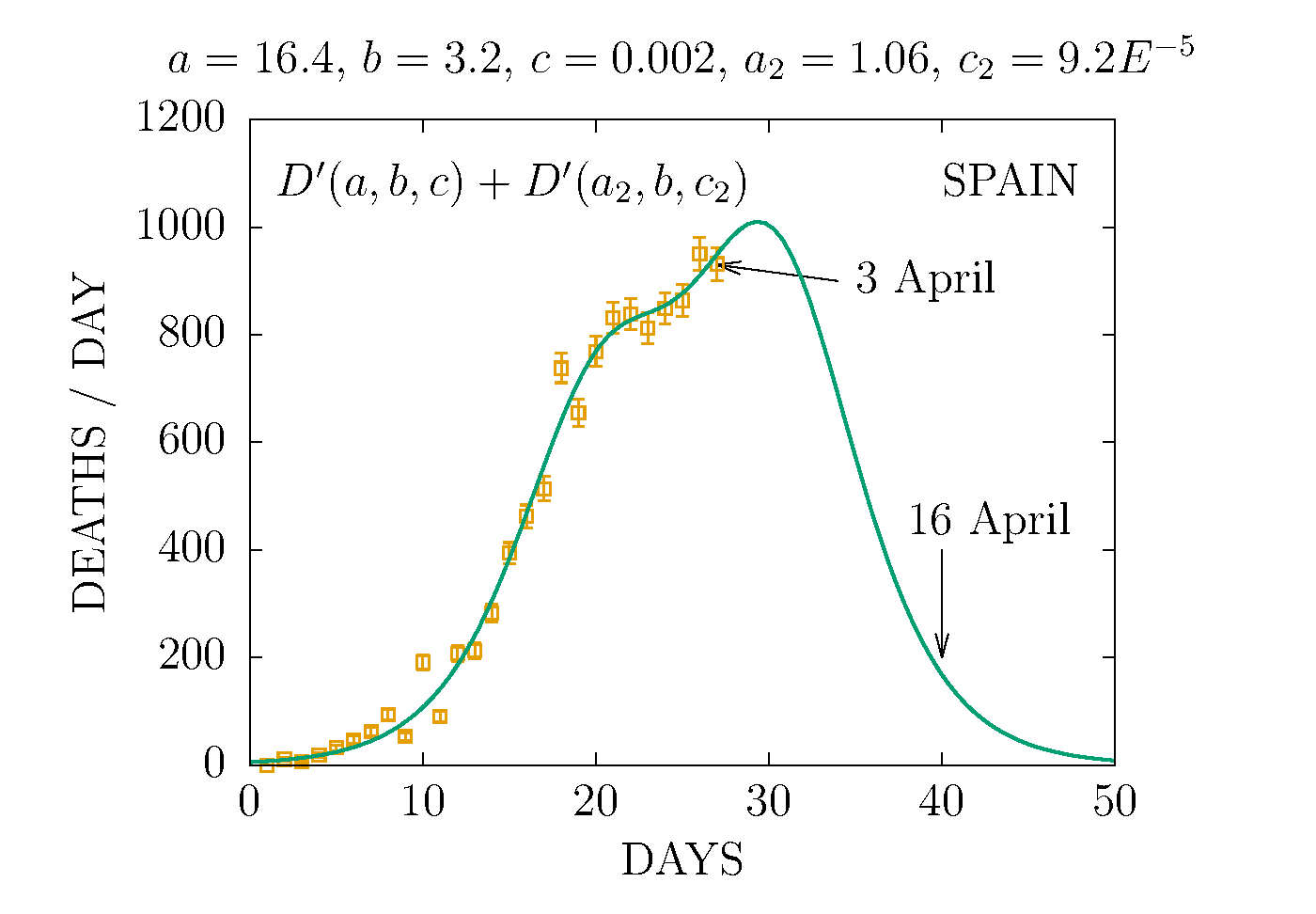 THE D'2 MODEL ASUMES TWO CHANNELS OF INFECTION 1 and 2 with different parameters
THE D'2 MODEL ASUMES TWO CHANNELS OF INFECTION 1 and 2 with different parameters
-
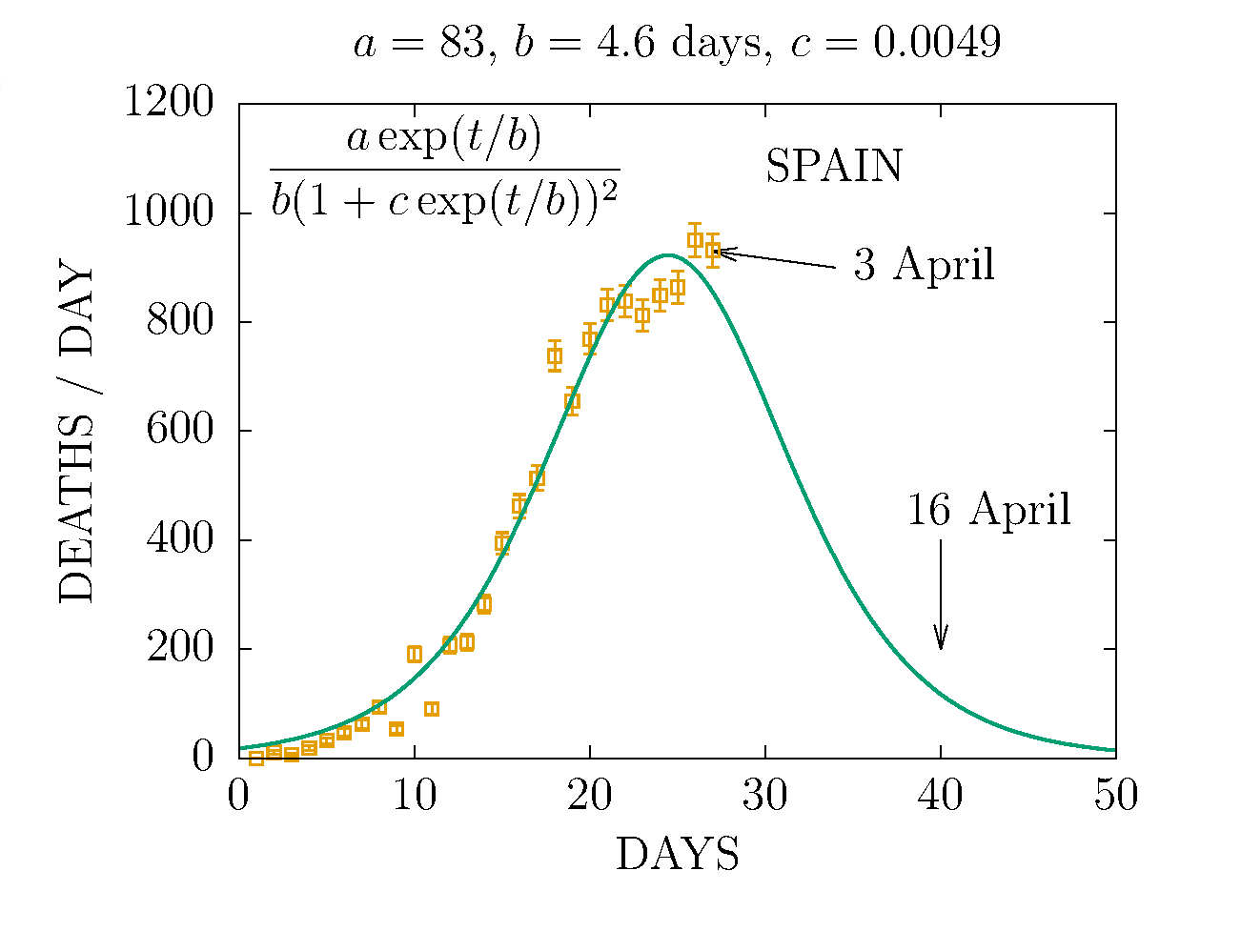
DEATHS PER DAY IN SPAIN 3 APRIL
-
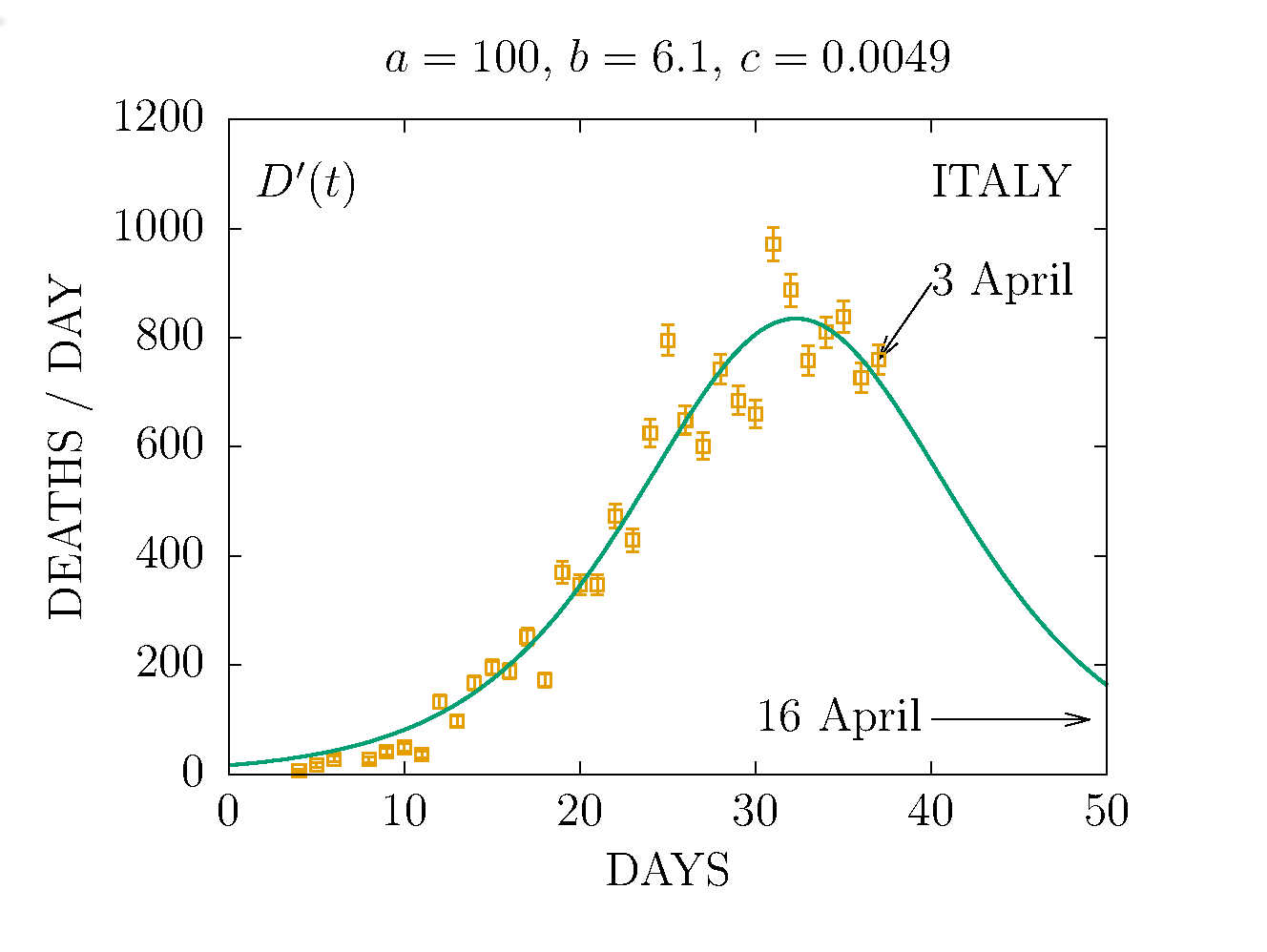
DEATHS PER DAY IN ITALY 3 APRIL
-
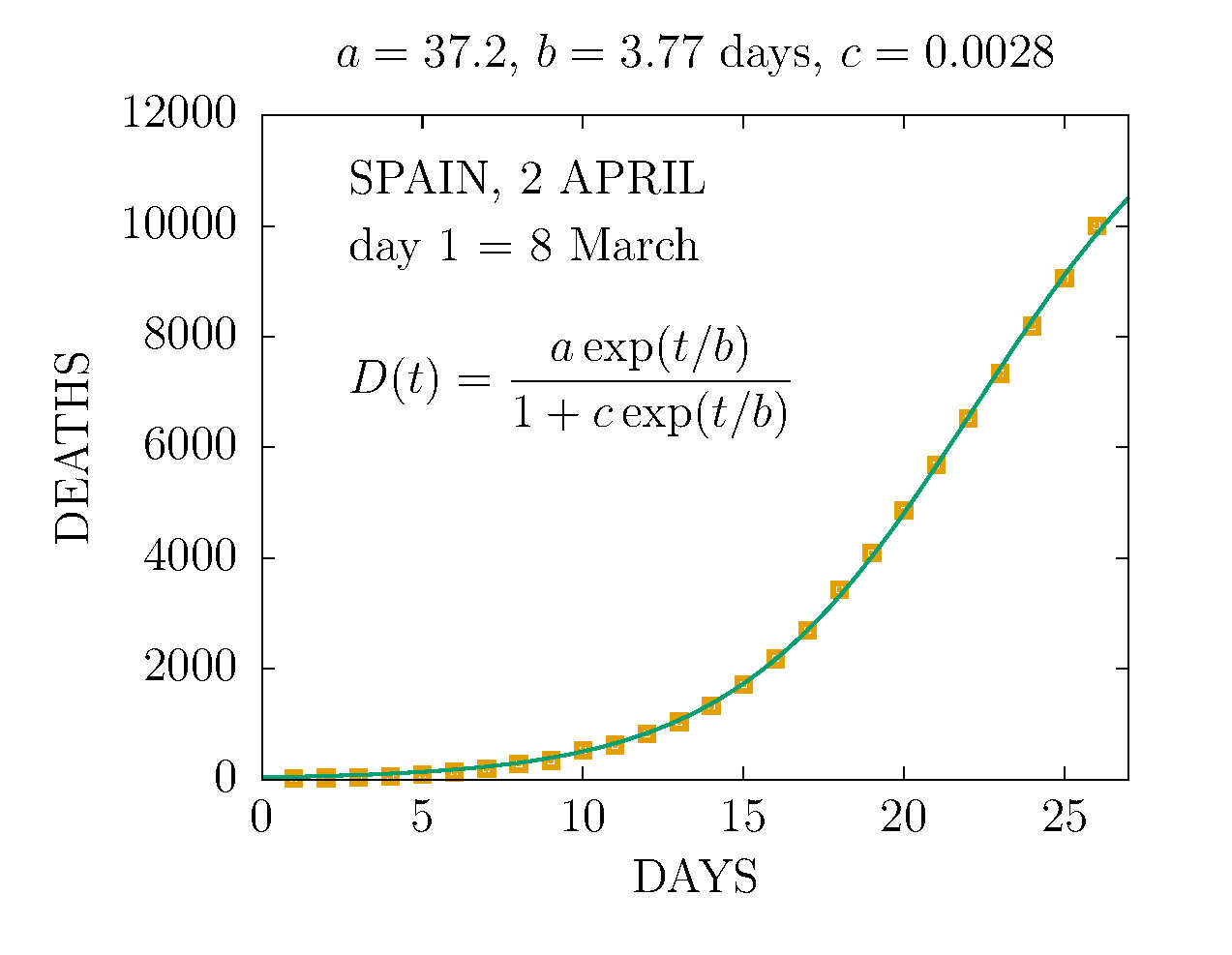
DEATHS IN SPAIN 3 APRIL (DAY 26TH)
-
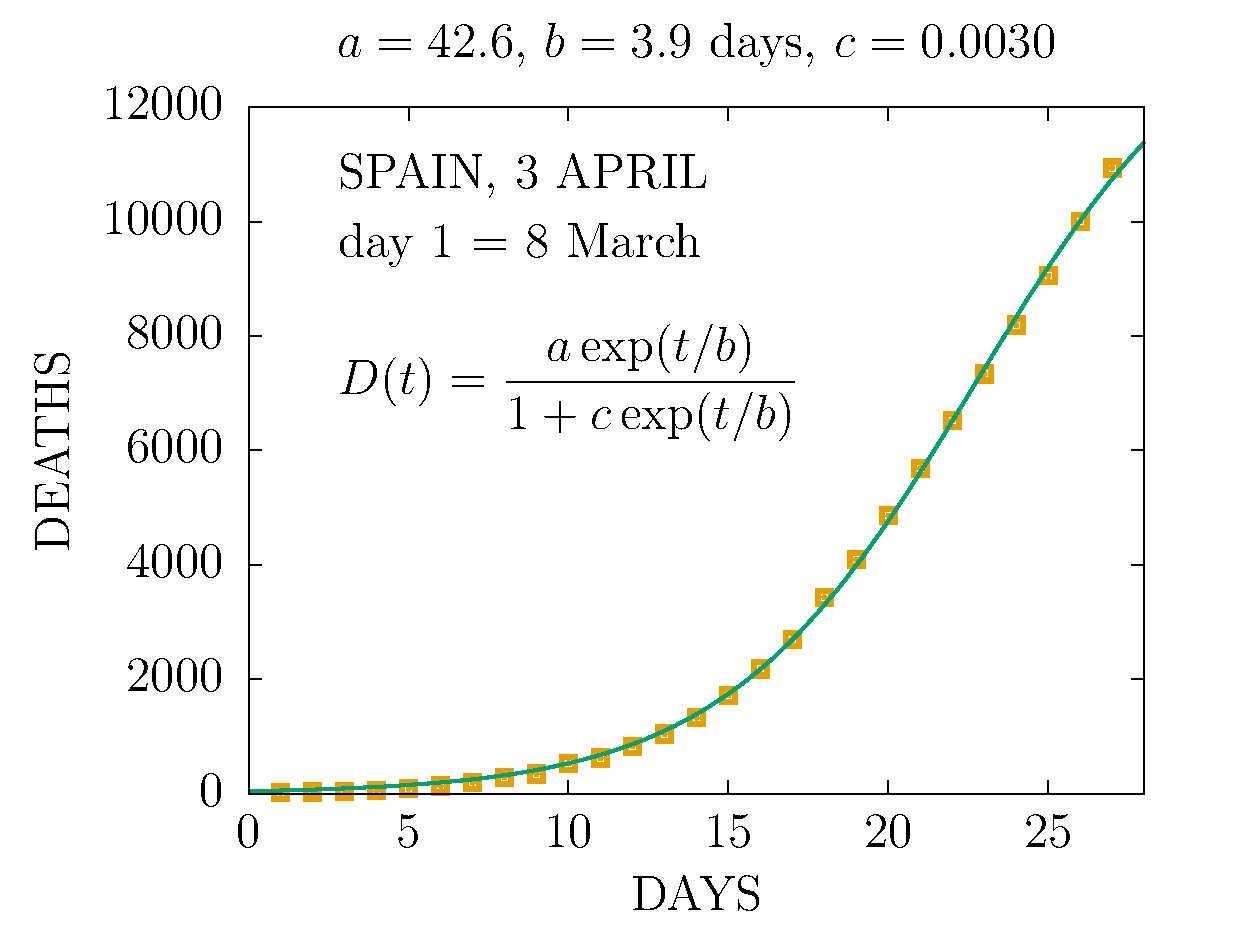
DEATHS IN SPAIN 2 APRIL (DAY 25TH)
-
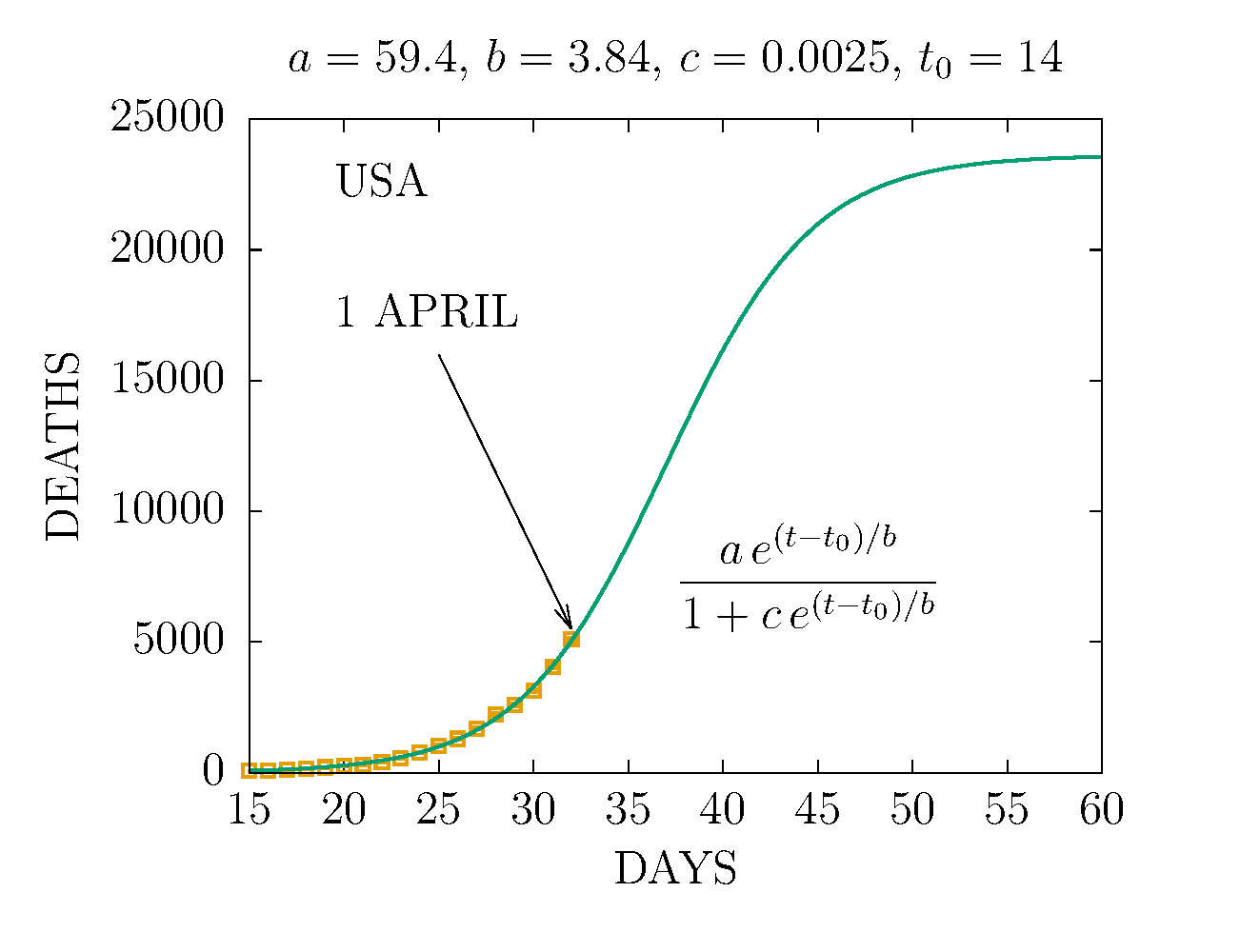
DEATHS IN USA 1 APRIL
-
DEATHS IN ITALY 1 APRIL
-
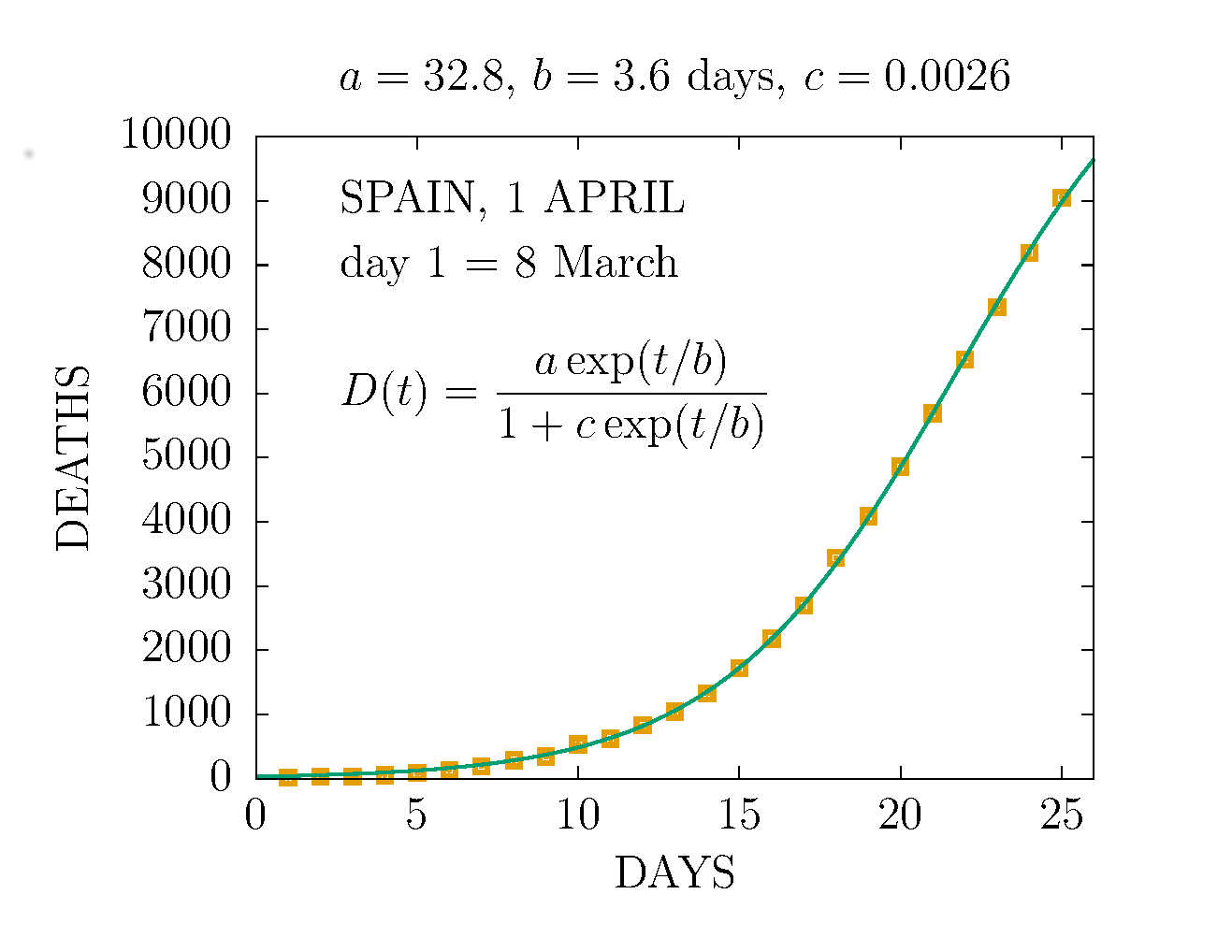
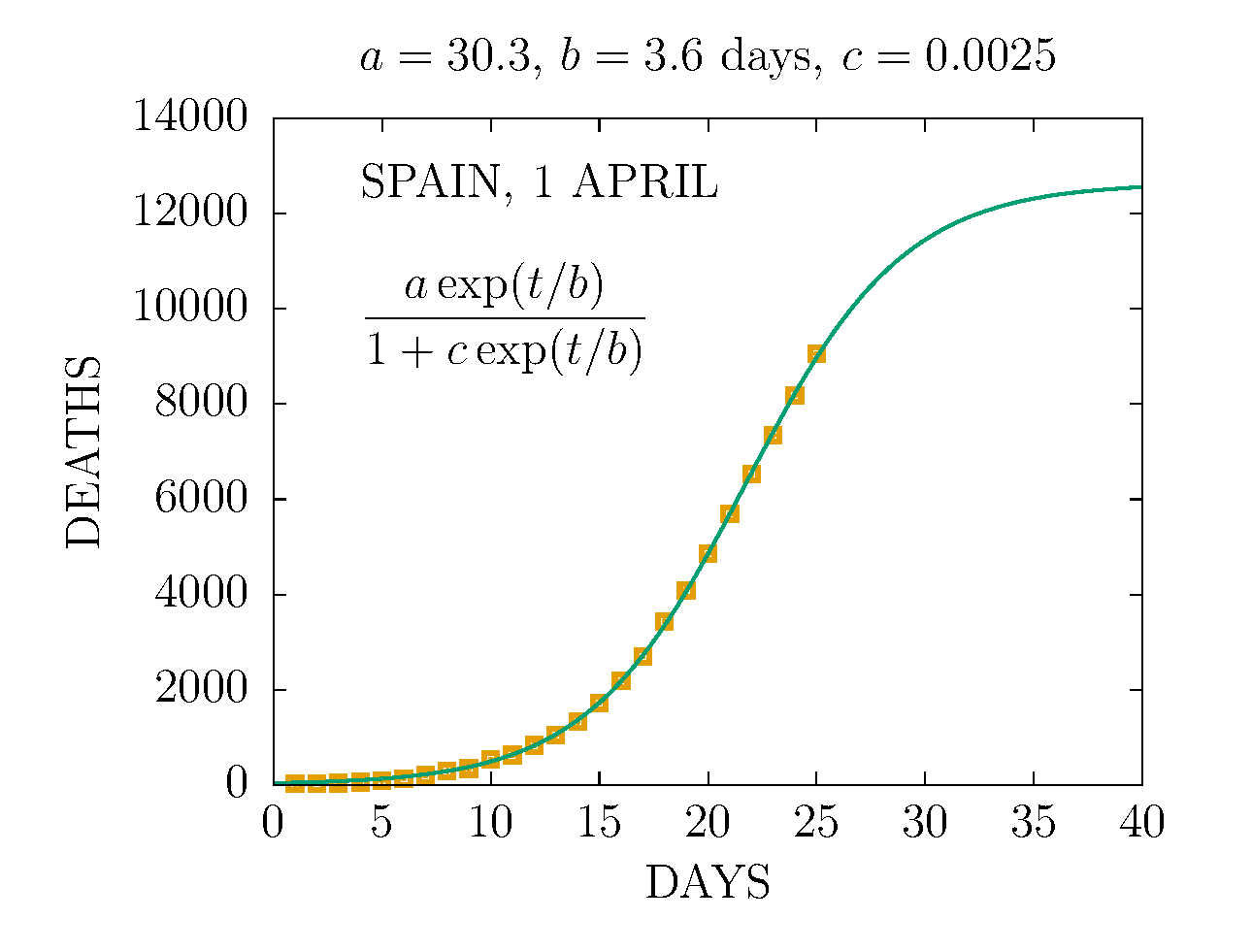
DEATHS IN SPAIN 1 APRIL (DAY 25TH)
-
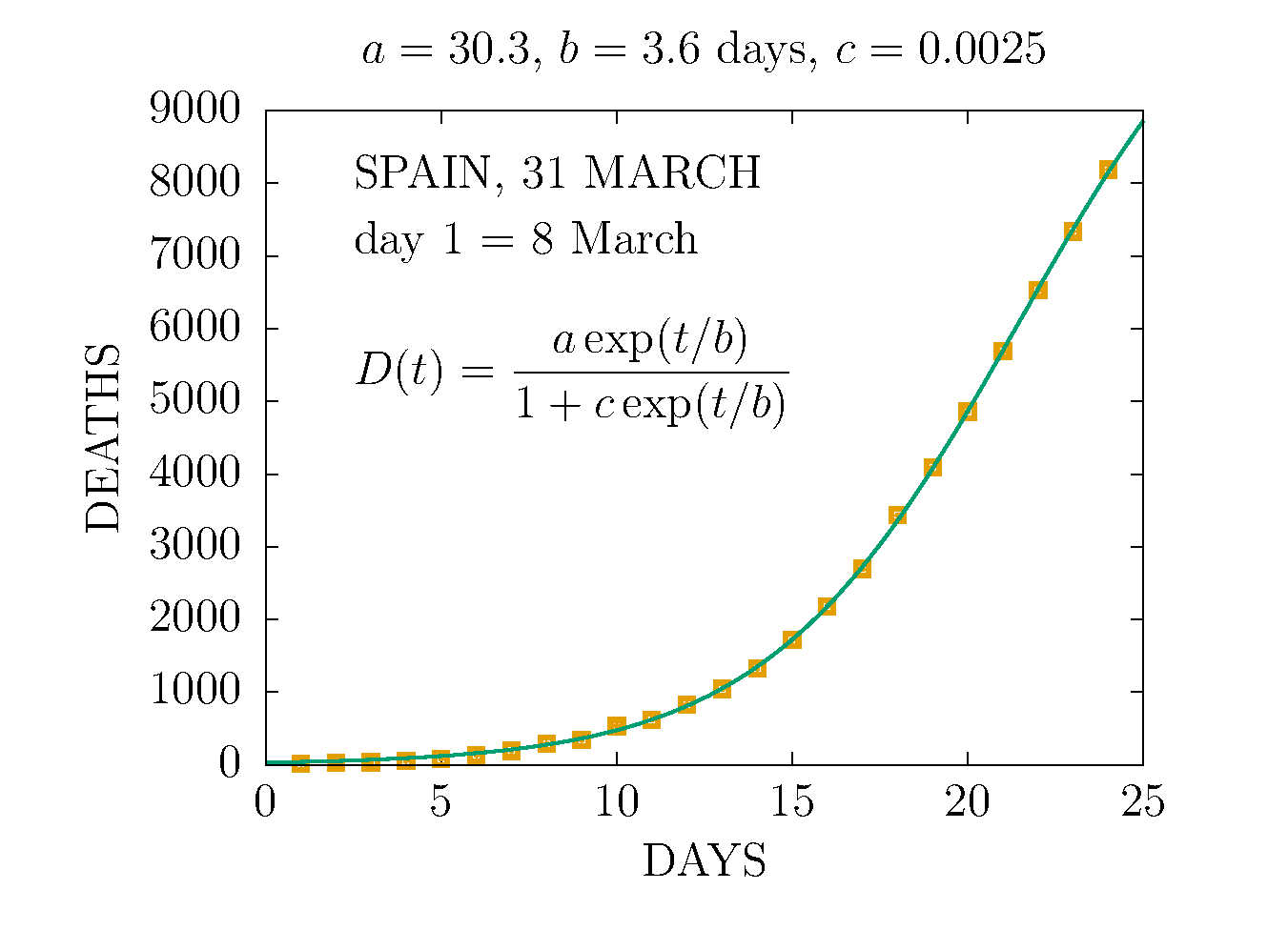
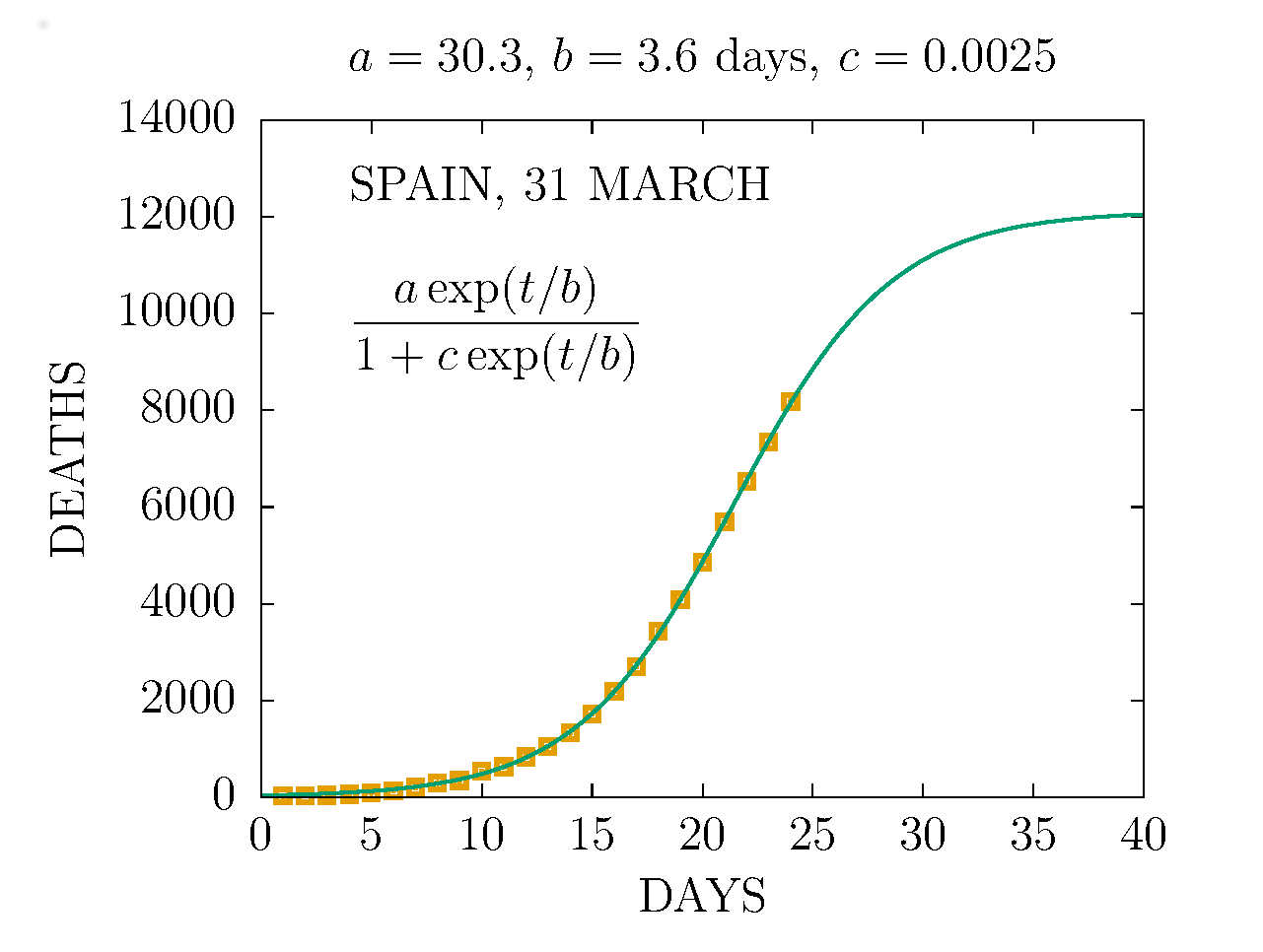
DEATHS IN SPAIN 31 MARCH (DAY 24TH)
-
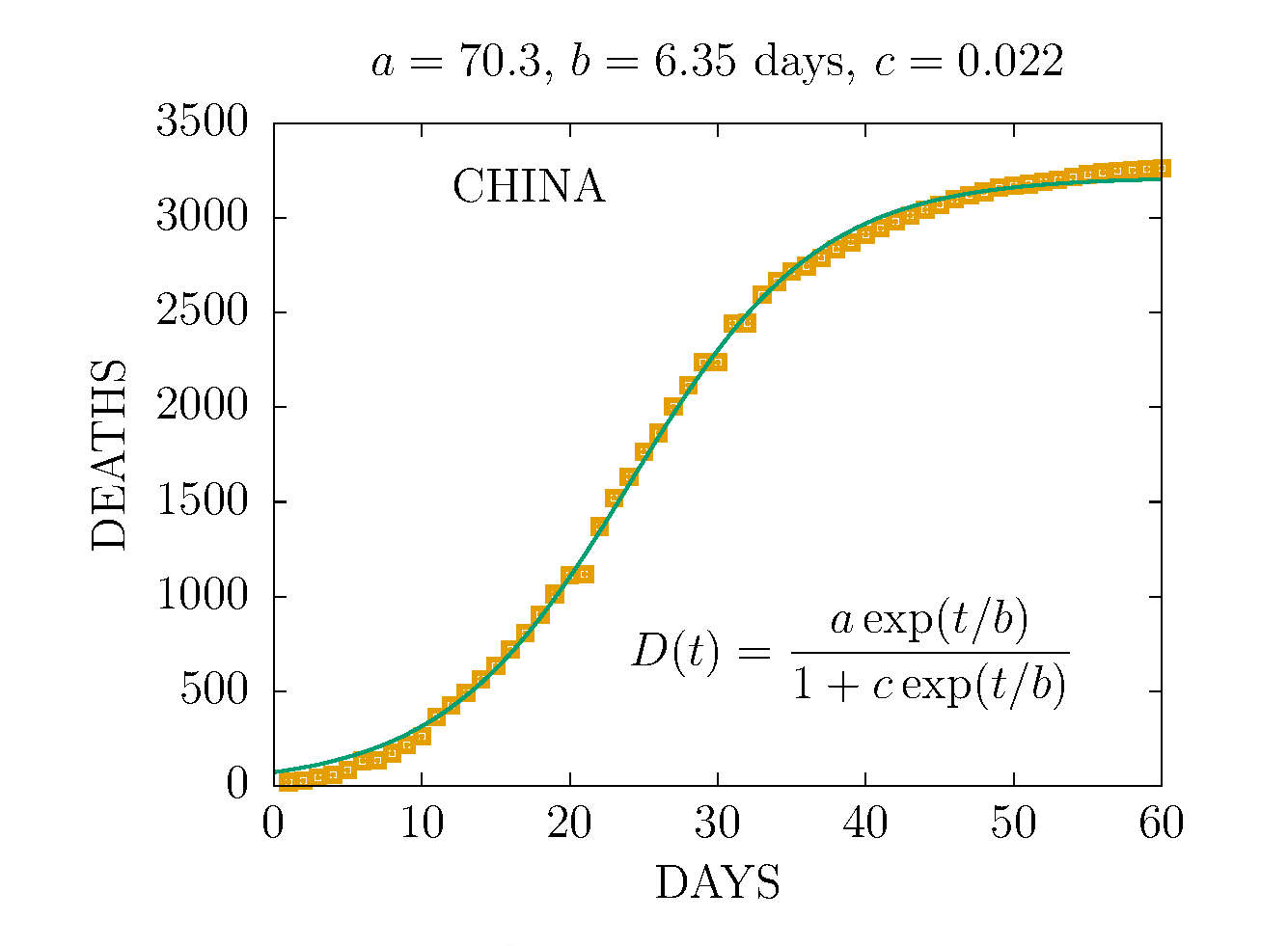
DEATHS IN CHINA
In china the pandemic is under control and they are at the top of
the D-curve
-
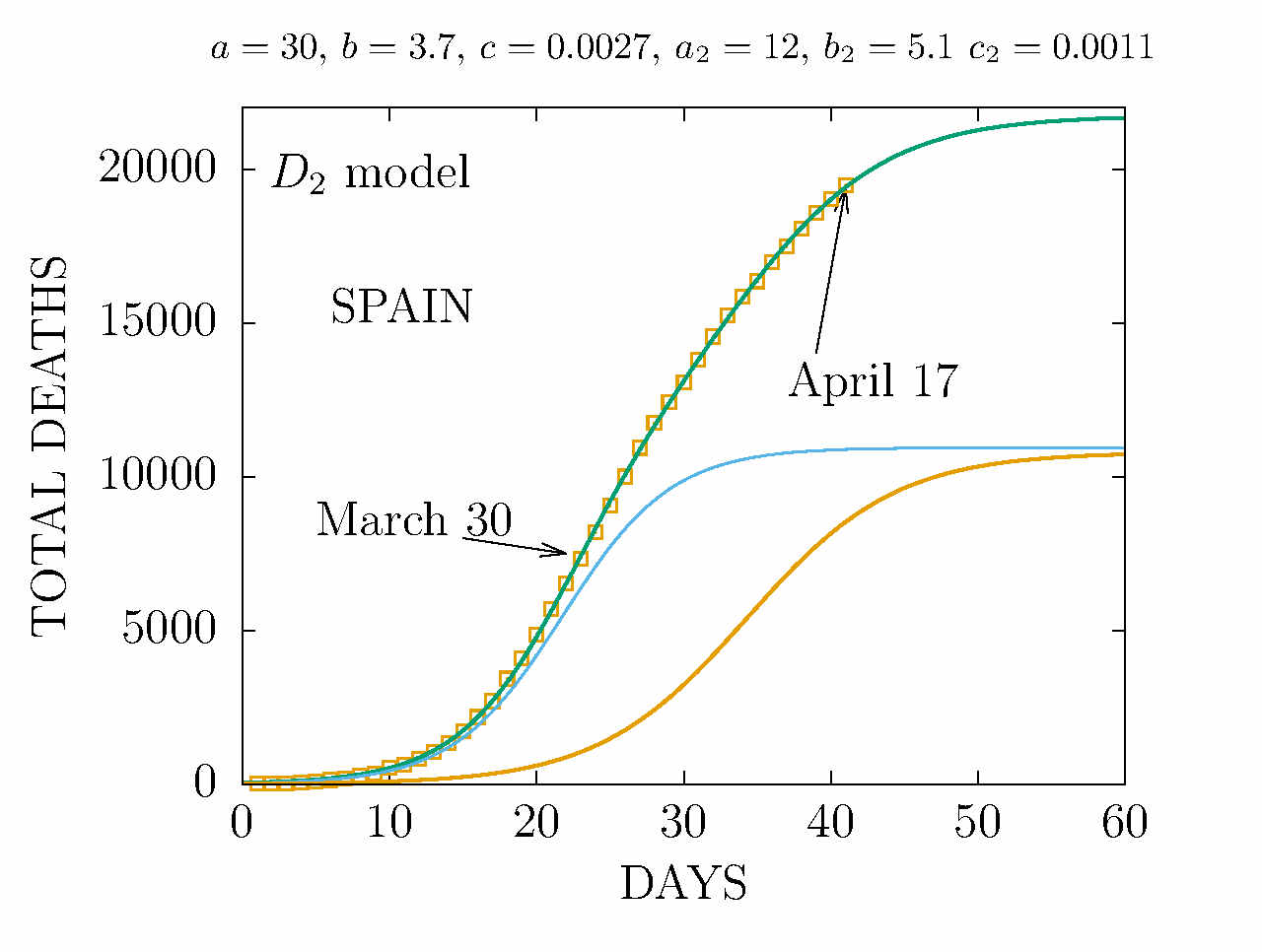
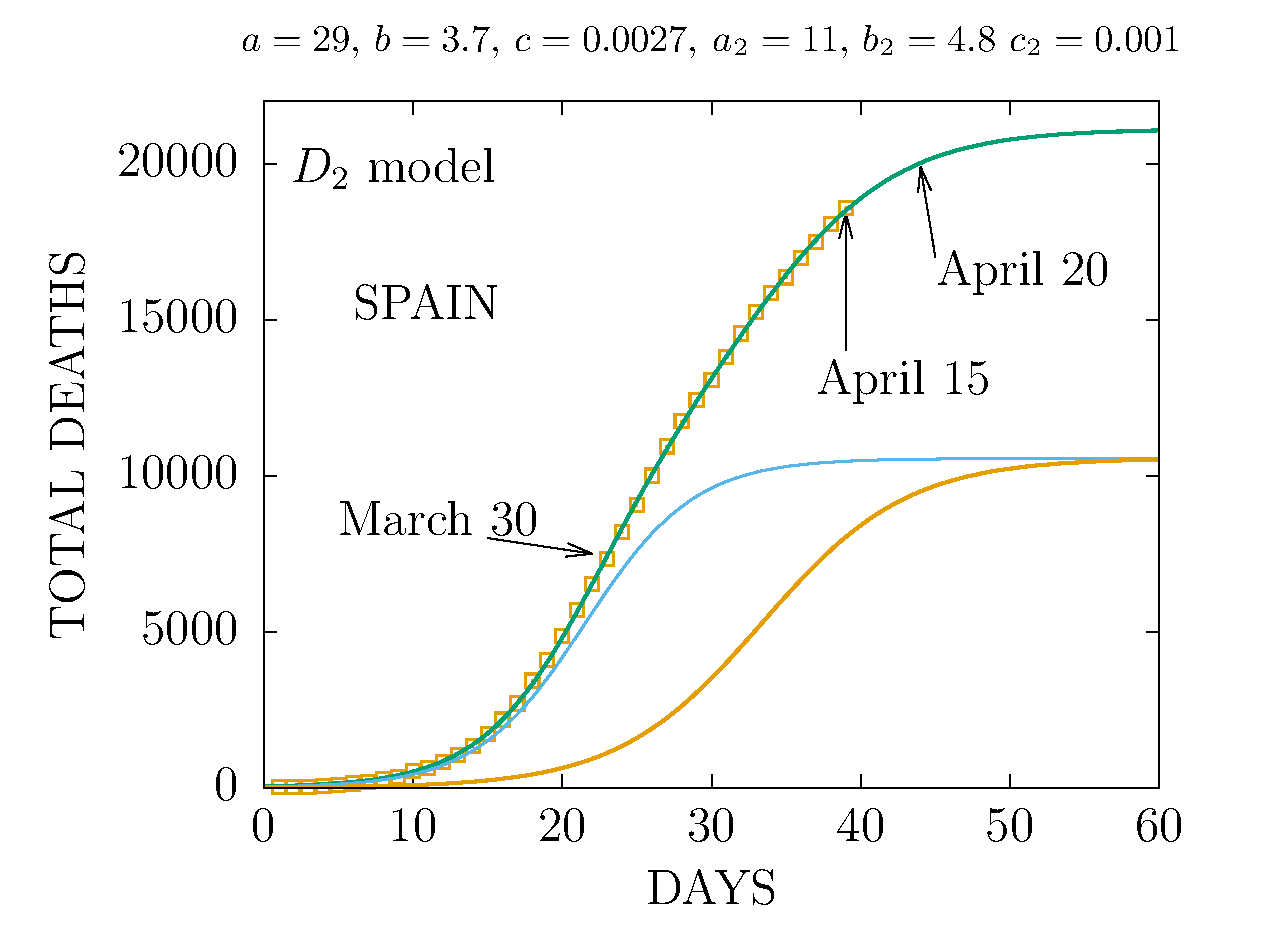
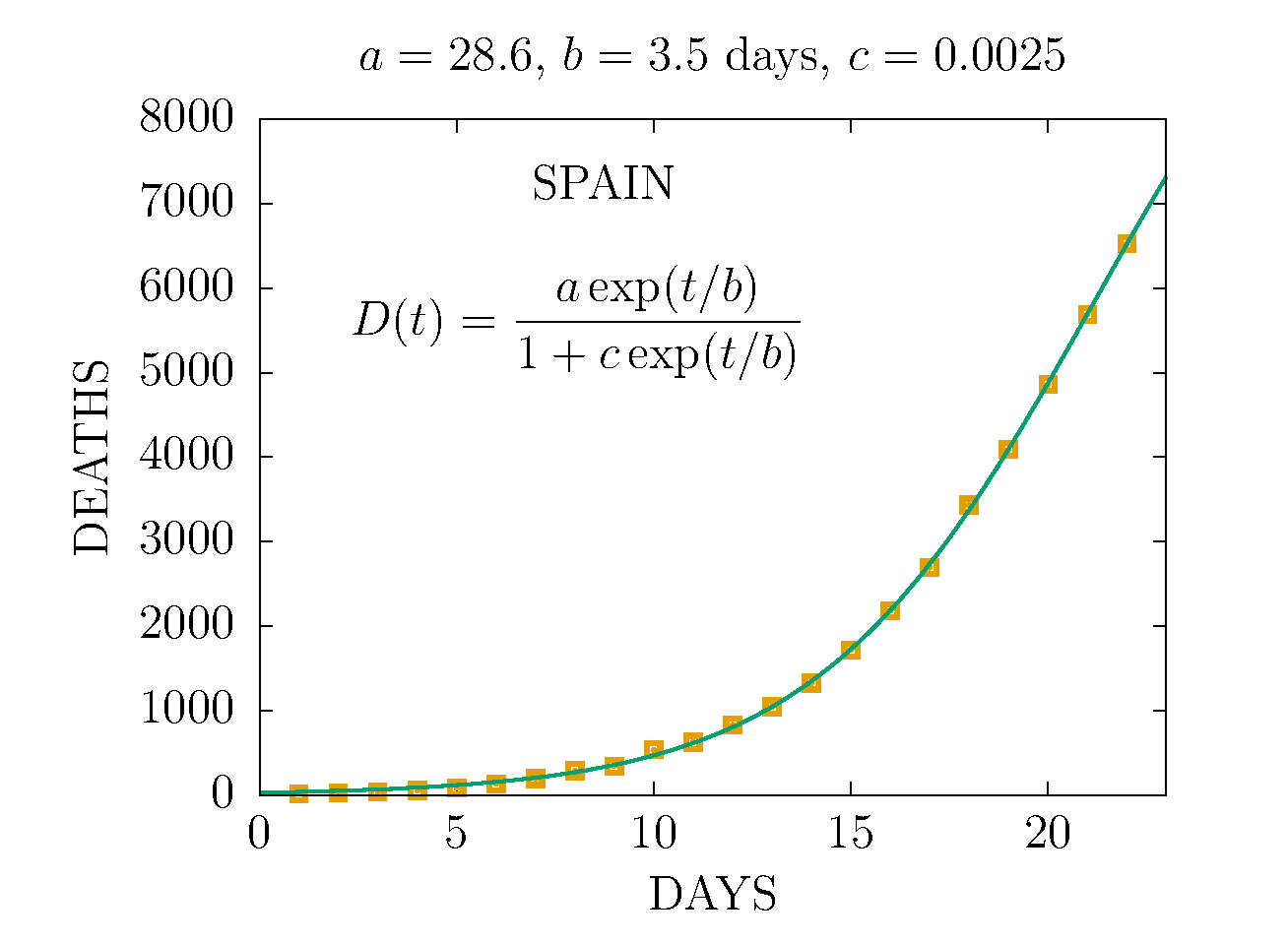
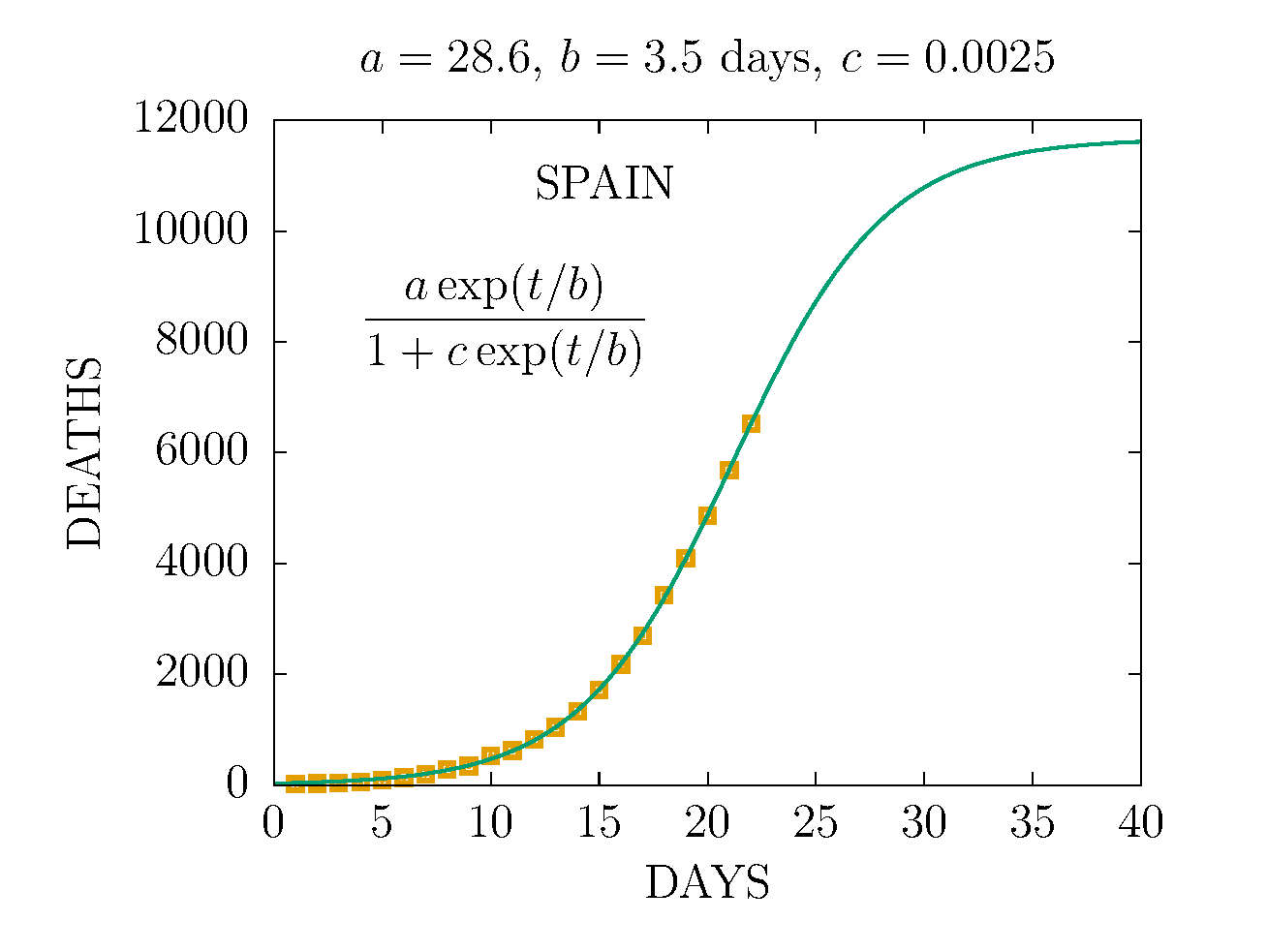
DEATHS IN SPAIN 30 MARCH (DAY 23TH)
The values of the parametes a, b, c are at the top of the plots
Click on the figures to enlarge
-
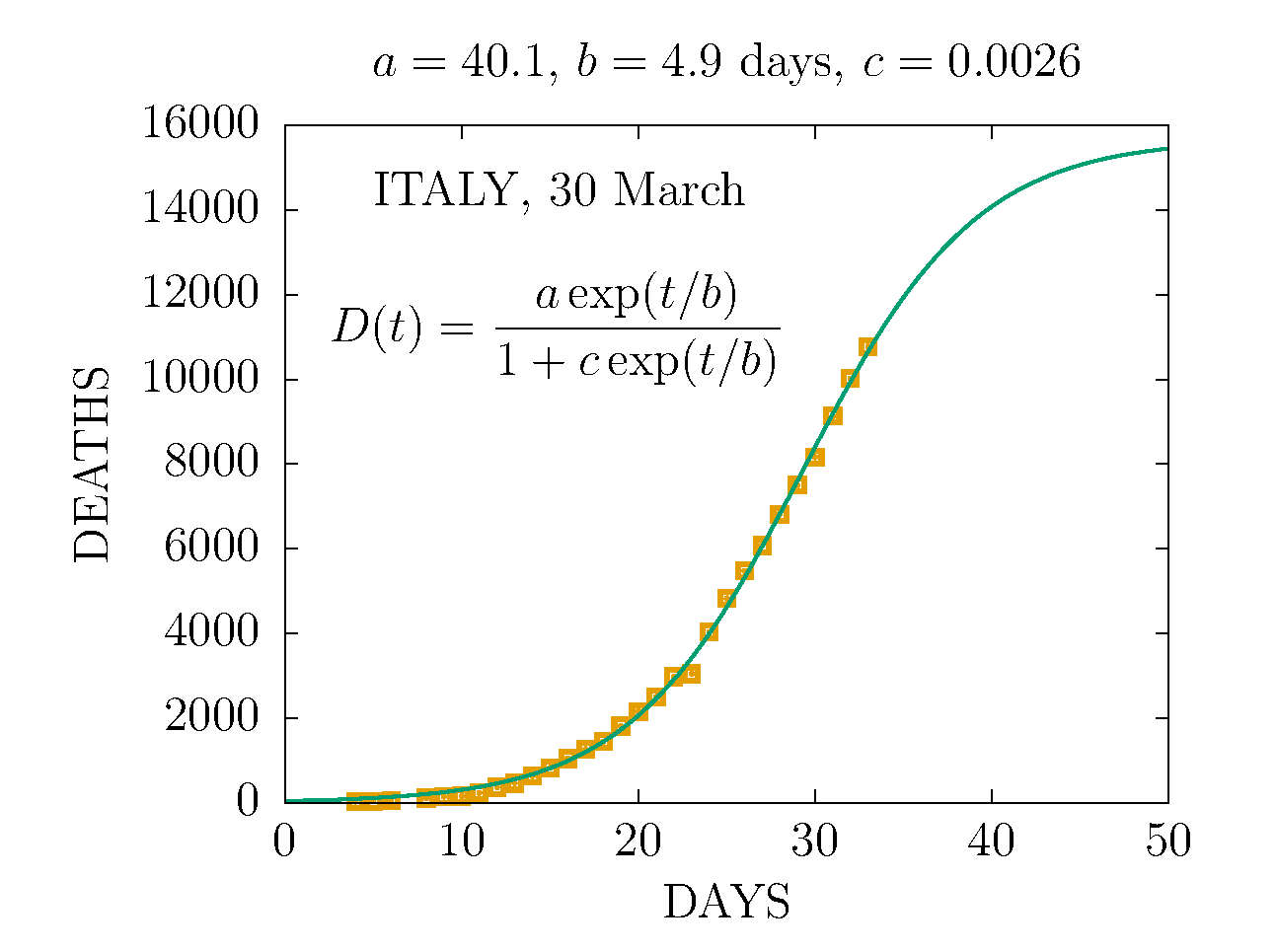
DEATHS IN ITALY 30 MARCH
-
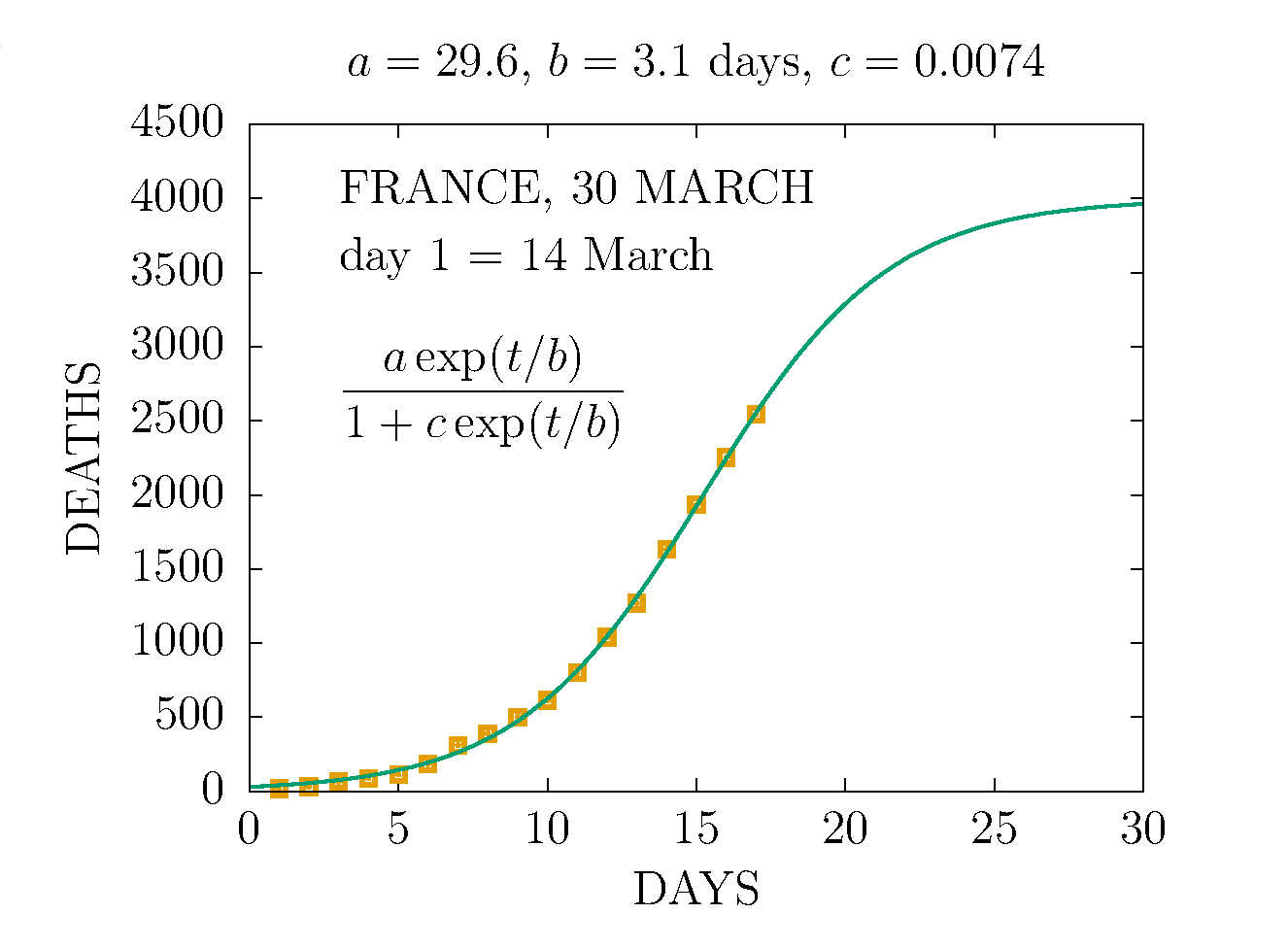
DEATHS IN FRANCE 30 MARCH
-
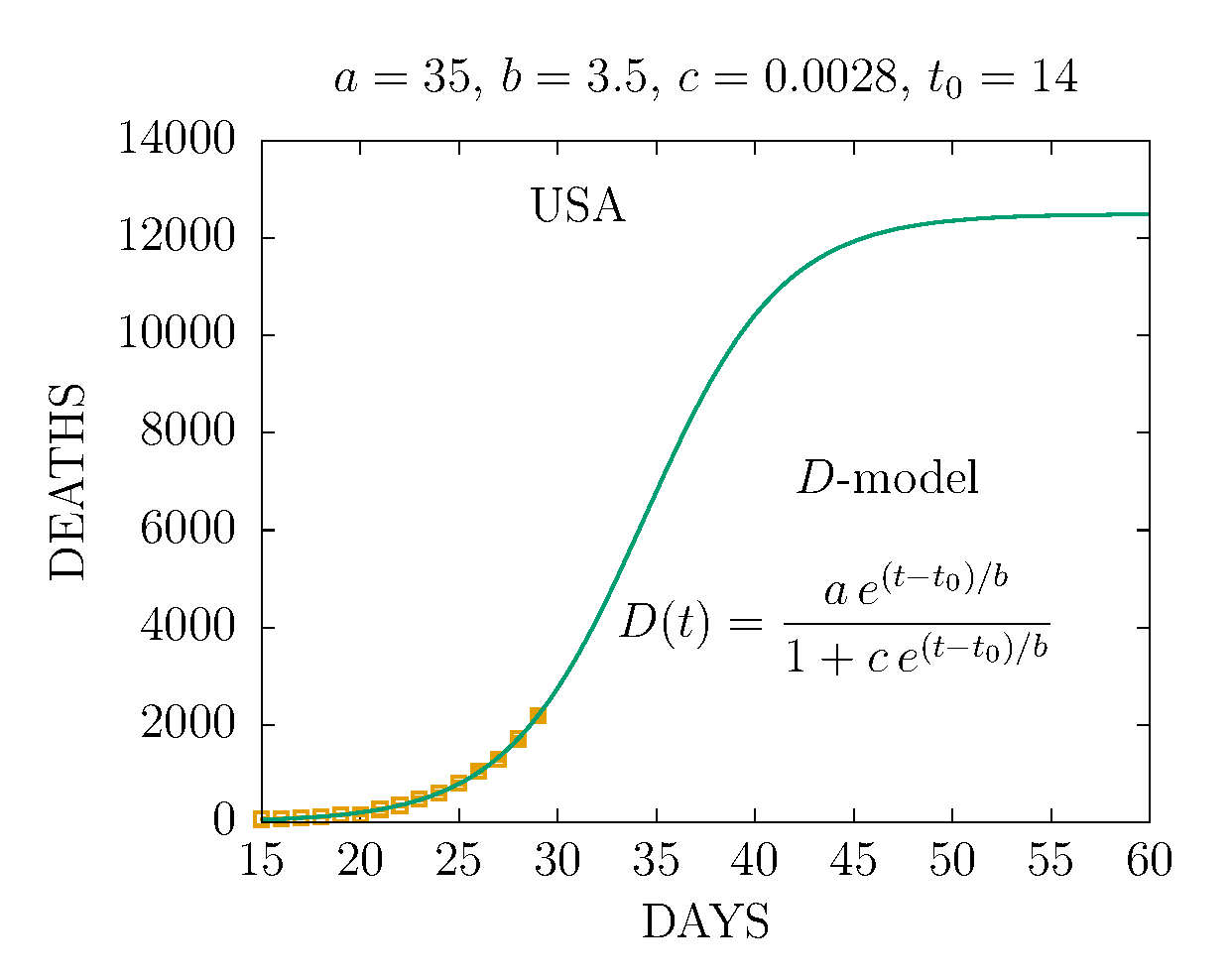
DEATHS IN USA DAY 29 MARCH
-
DEATHS IN SPAIN DAY 22 (29 MARCH)
-
2. THE D MODEL OF DEATHS BY CORONAVIRUS
This is a summary of the paper
The D model for deaths by COVID-19
by J.E. Amaro
The D model (D is for deaths) derives form the SIR model
(susceptible, infected, recovered) as a particular case with an
analytical solution. We assume that the recoved individuals have no
effect on the infection rate.
The D model is based on two hypothesis:
1. The infection rate over time is proportional to the infected and
non-infected individuals (SI model) :
dI(t) = lambda I(t) ( N - I(t) ) dt
where N is the total population exposed to the virus.
2. The number of deaths at some time t is
proportional to the infestation at some former time T.
Therefore we define the D-function as
D(t) = mI(t − T )
Where m is the mortality or death rate, and T is the mortality time.
With this assumption we can write the D function as
D(t) = a exp(t/b) / ( 1 + c exp (t/b) )
The three constants a, b, c are the parameters of the model. They
are obtained by fit to actual data for the first pandemia days and
they can be used to make predictions for the next days.
The D-model for COVID-19 pandemic describes well the current data
of several countries, including China, Spain and Italy with only
three parameters.
The assumption made in the SI model is that the recovered
individuals do not influence the increase of the infected ones, This
hypothesis does not seem to be very bad since the model reproduces
well the data up to now. This could indicate that the
total population N is not a constant as assumed in the SIR model,
but it increases over time as more people are exposed, for example,
in villages that until now had been isolated from the sources of
infection in big cities.
The D model is simple enough to provide fast
estimations of pandemic evolution in other countries, and could be
useful for the control of the disease.
-
3. OLD FITS
-
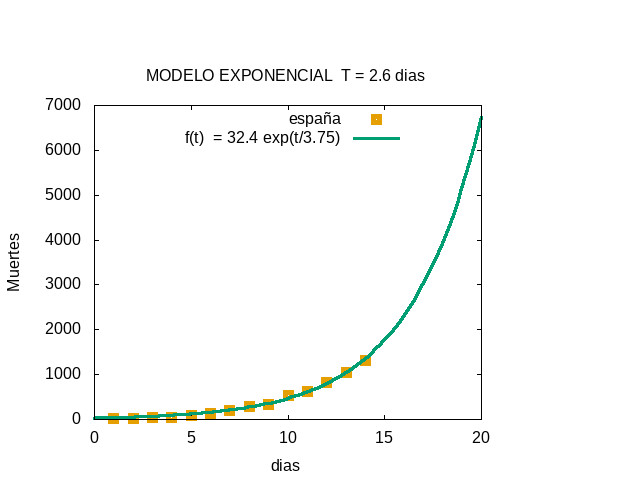
FIRST FIT - MARCH 21 (DAY 14)
Exponential fit (t in days)
The resulting funtion was f(t) = 32.4 exp( t / 3.75 )

The time T = 3.75 log(2) = 2.6 days is the time to get twice the number of deaths
This fit predicted about 1800 deaths the next day. The actual value was 1720
-
PREDICTION FOR THE NEXT 5 DAYS
This fit allowed to predict the deaths for ne next days.
It was estimated about 7000 deaths for day 20 (saturday march 28).
This is shown in the next figure;
----------------------------------------------
-
SECOND FIT - SUNDAY MARCH, 22 (DAY 15)
The exponential fit gave f(t) = 34.3 exp( t / 3.8 )
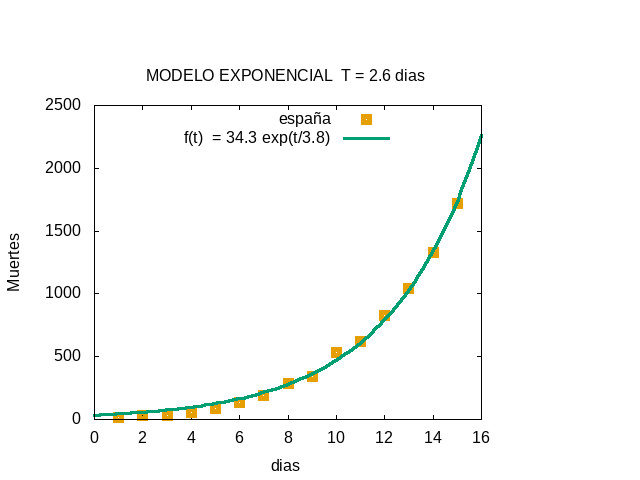
The twice time was T = 3.8 log(2) = 2.6 days
The constant in the exponent, b = 3.8 days, increased by 0.05
days with respect to the previous fit, which indicates that the
behaviour is not purely exponential, but somewhat slower.
This fit predicted about 2200 deaths the next day.
The actual value was 2182
-
5-days prediction
The model estimated 6500 death for the day 20 (saturday, march 28),
less than the previous estimation.
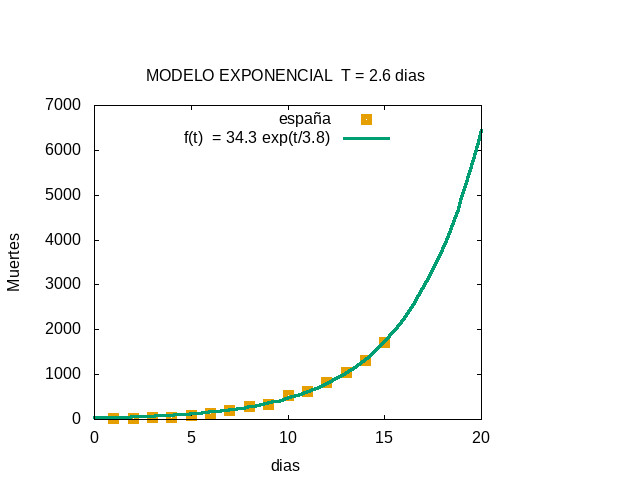 ----------------------------------
----------------------------------
-
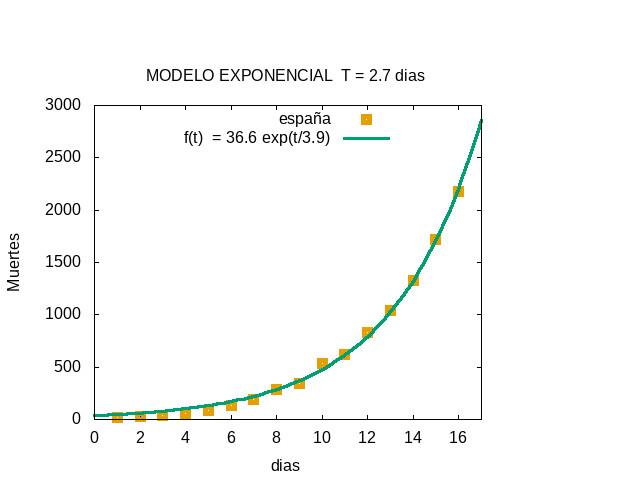
TERCER AJUSTE - LUNES 23 DE MARZO - Evolución exponencial hasta el día 16
Ajuste exponencial realizado con gnuplot (tiempo t en días)
La función ajustada fue f(t) = 36.6 exp( t / 3.9 )
El tiempo de doblaje T = 3.9 log(2) = 2.7 días es el tiempo que tiene que transcurrir para que el número de muertes se multiplique por dos.
La constante de tiempo en el exponente, 3.9 días, aumentó en 0.1 con respecto al ajuste anterior, lo que indica que el aumento no es puramente exponencial sino algo ligeramente más lento.
Este ajuste predecía unas 2700 muertes al día siguiente. El valor real fue de 2696.
-

Predicción a 5 días
El ajuste permitía estimar el número de muertes los días sucesivos. Este valor se estimó en cerca de 8000 para el día 21 (doming 29 de marzo),.
-
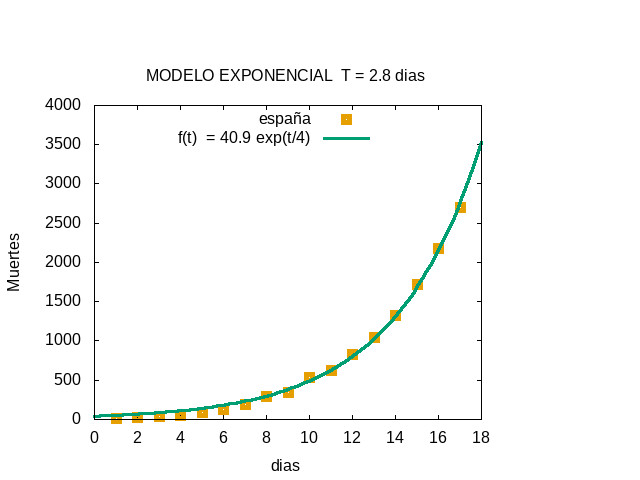
CUARTO AJUSTE - MARTES 24 DE MARZO - Evolución exponencial hasta el día 17
Ajuste exponencial realizado con gnuplot (tiempo t en días)
La función ajustada fue f(t) = 40.9 exp( t / 4 )
El tiempo de doblaje T = 4 log(2) = 2.8 días es el tiempo que tiene que transcurrir para que el número de muertes se multiplique por dos.
La constante de tiempo en el exponente, 4 días, aumentó en 0.1 con respecto al ajuste anterior, lo que indica que el aumento no es puramente exponencial sino algo ligeramente más lento.
Este ajuste predecía unas 3500 muertes al día siguiente. El valor real fue de 3434.
-
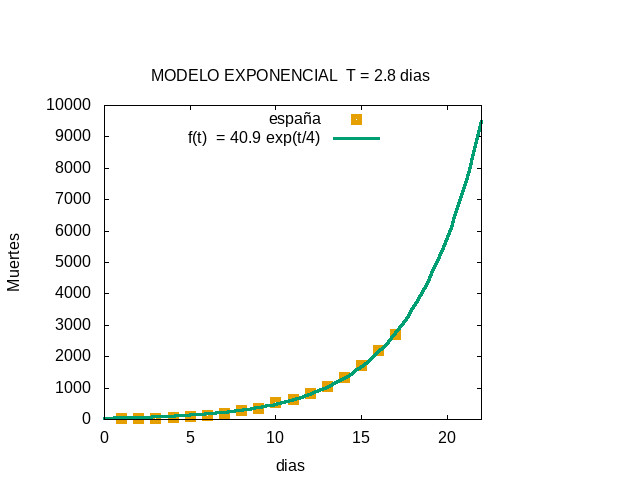
Predicción a 5 días
El ajuste permitía estimar el número de muertes los días sucesivos. Este valor se estimó en cerca de 8000 para el día 21 (doming 29 de marzo),.
-
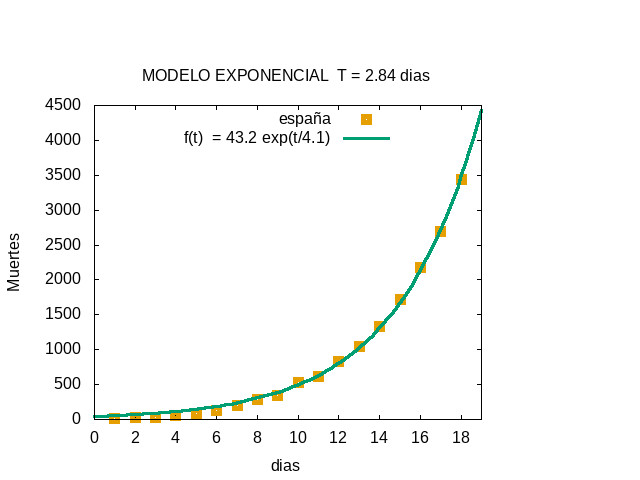
QUINTO AJUSTE - MIERCOLES 25 DE MARZO - Evolución exponencial hasta el día 18
Ajuste exponencial realizado con gnuplot (tiempo t en días)
La función ajustada fue f(t) = 43.2 exp( t / 4.1 )
El tiempo de doblaje T = 4.1 log(2) = 2.84 días es el tiempo que tiene que transcurrir para que el número de muertes se multiplique por dos.
La constante de tiempo en el exponente, 4.1 días, aumentó en 0.1 con respecto al ajuste anterior, lo que indica que el aumento no es puramente exponencial sino algo ligeramente más lento.
Este ajuste preveía unas 4500 muertes al día siguiente, jueves 26 de abril.
-
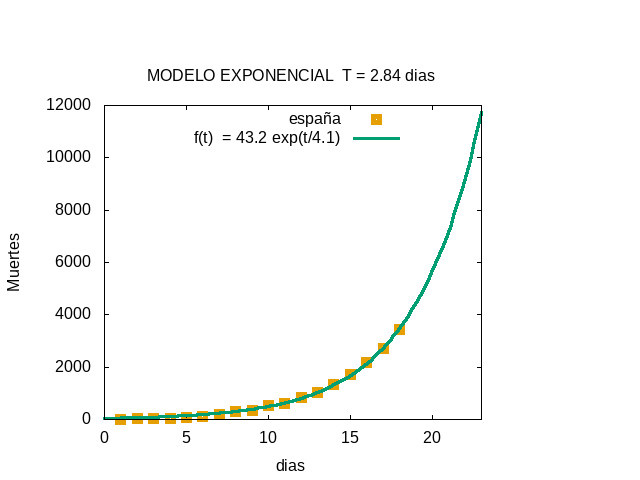
Predicción a 5 días
El ajuste permitía estimar el número de muertes los días sucesivos. Este valor se estimó en cerca de 9500 para el día 22 (lunes 30 de marzo),.
-
NUEVO MODELO MESETA - MIERCOLES 25 DE MARZO - Ajuste hasta el día 18
El modelo exponencial solo es válido al inicio de la pandemia
El modelo meseta supone que el número de contagios es proporcional al número de contagiados
y también al número de no contagiados
dN = p (A-N) N dt
p es una constante
N es el número de contagios
A es la población total
La solución de esta ecuación diferencial es
N(t) = a exp( t/b)/( 1-c + c exp(t/b))
Veremos que el parámetro c es mucho menor que uno, y se puede aproximar 1-c =1 en el denominador
Los parámetros ajustados con los datos hasta este dia son
a= 30.5
b= 3.6 dias
c = 0.0021 << 1
Esta funcion inicialmente crece de forma exponencial pero algo más lenta, como se ve a continución;
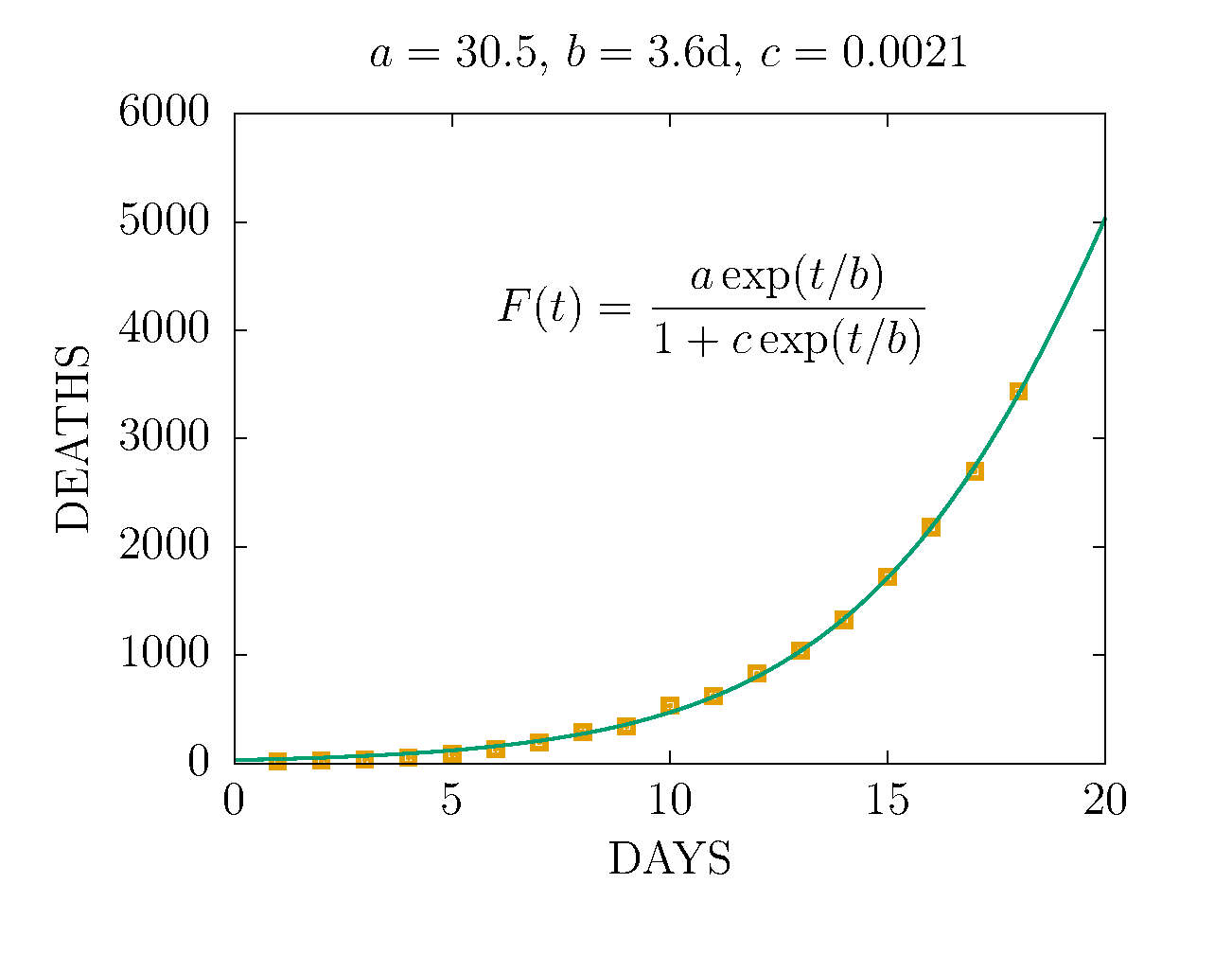
Sin embargo la función tiende a una constante, alcanzando un plateau alrededor de 30 días,
ES DECIR, EL 8 DE ABRIL, como se ve a continuación
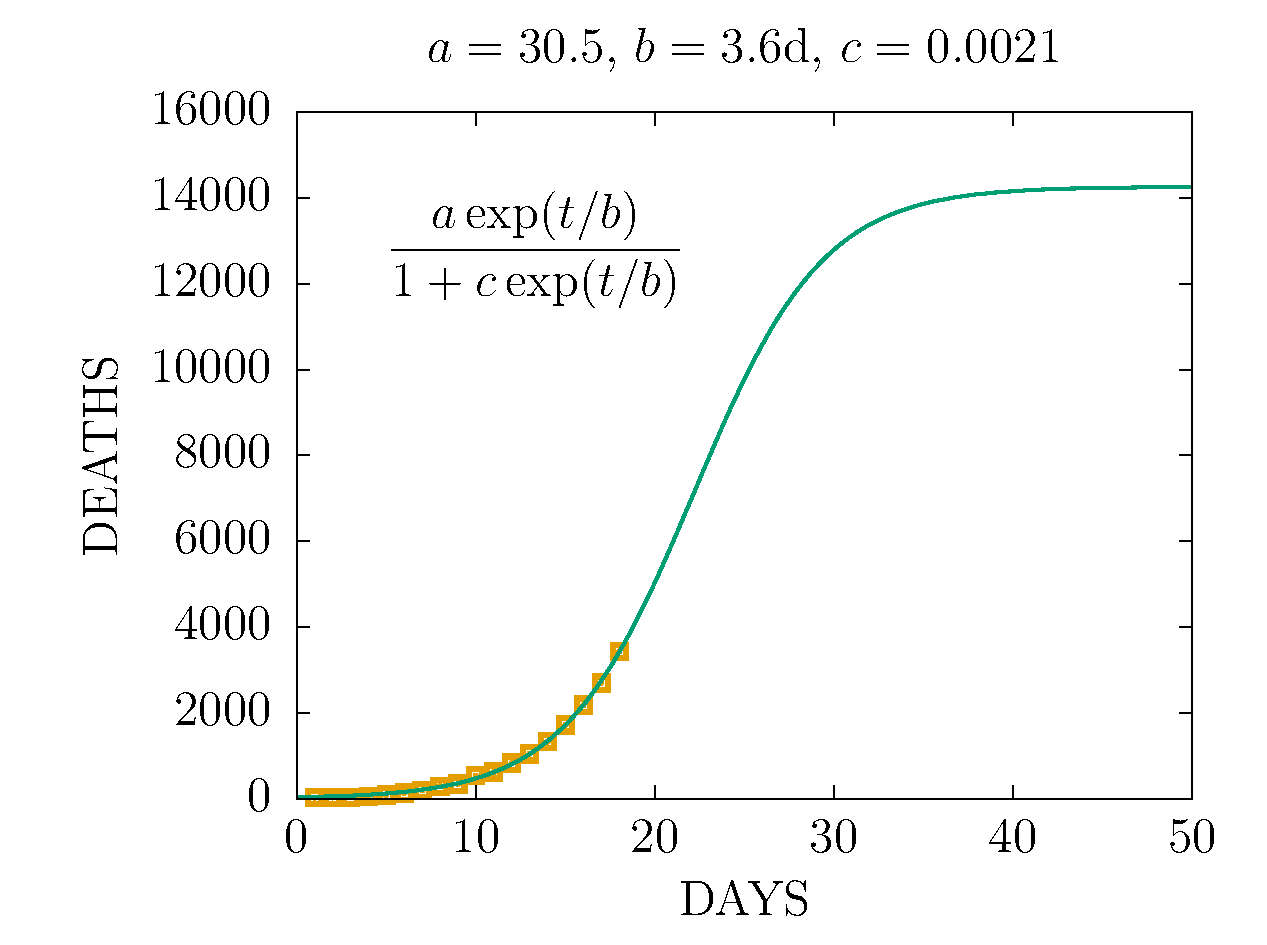
-
MODELO MESETA - JUEVES 26 DE MARZO - Ajuste hasta el día 19
El modelo meseta supone que el número de contagios es proporcional al número de contagiados
y también al número de no contagiados
N(t) = a exp( t/b)/( 1-c + c exp(t/b))
Los parámetros ajustados con los datos hasta este dia son
a= 28.5
b= 3.5 dias
c = 0.0024 << 1
Esta funcion inicialmente crece de forma
exponencial pero algo más lenta, como se ve a continuación.
Se compara con la función exponencial que se ajustó el día anterior
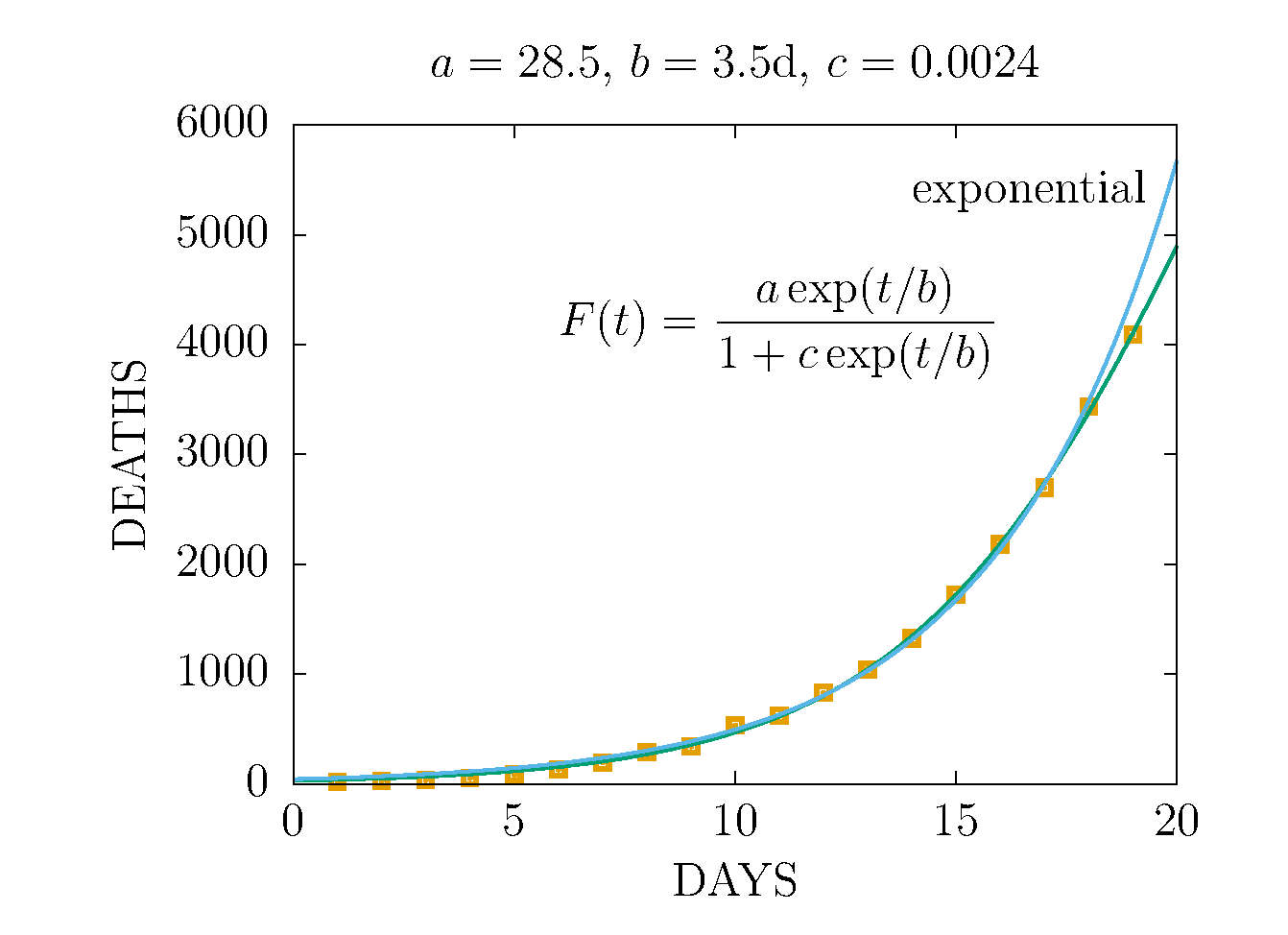
Esta función tiende a una constante, alcanzando un plateau en unos 30 días,
ES DECIR, EL 8 DE ABRIL, como se ve a continuación
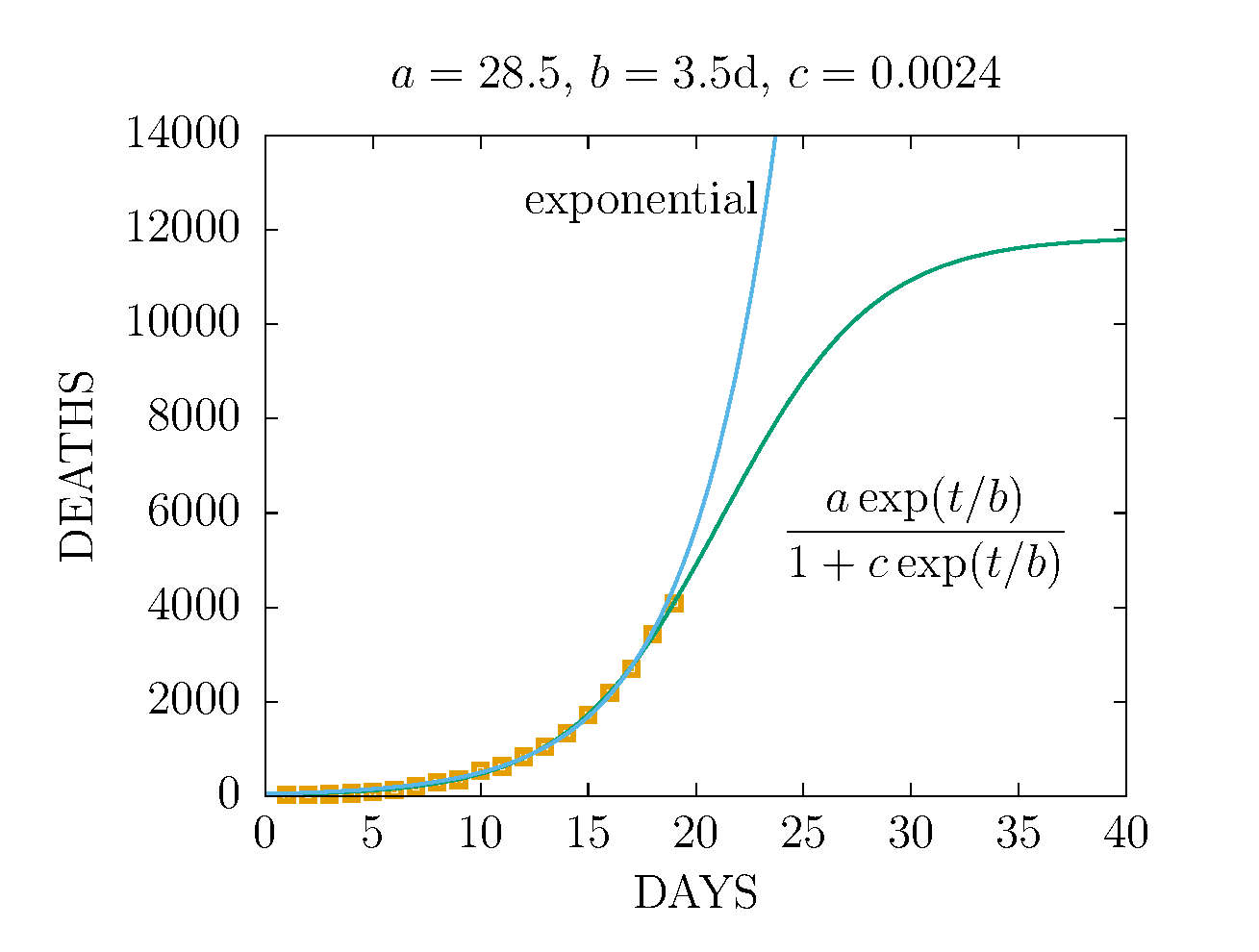 ------------------------------------------------------------
------------------------------------------------------------
-
SPAIN DATA
DAY DEATHS DATE(month.day)
----(Series empieza el 8 de marzo)------------------
1 17 3.08 domingo
2 28 3.09
3 35 3.10
4 54 3.11
5 86 3.12
6 133 3.13
7 195 3.14 sabado
8 289 3.15
9 342 3.16
10 533 3.17
11 623 3.18
12 830 3.19
13 1043 3.20
14 1326 3.21 sabado
15 1720 3.22
16 2182 3.23
17 2696 3.24
18 3434 3.25
19 4089 3.26
20
21
Actualizado al 26 de marzo de 2020, hora de España 12:00
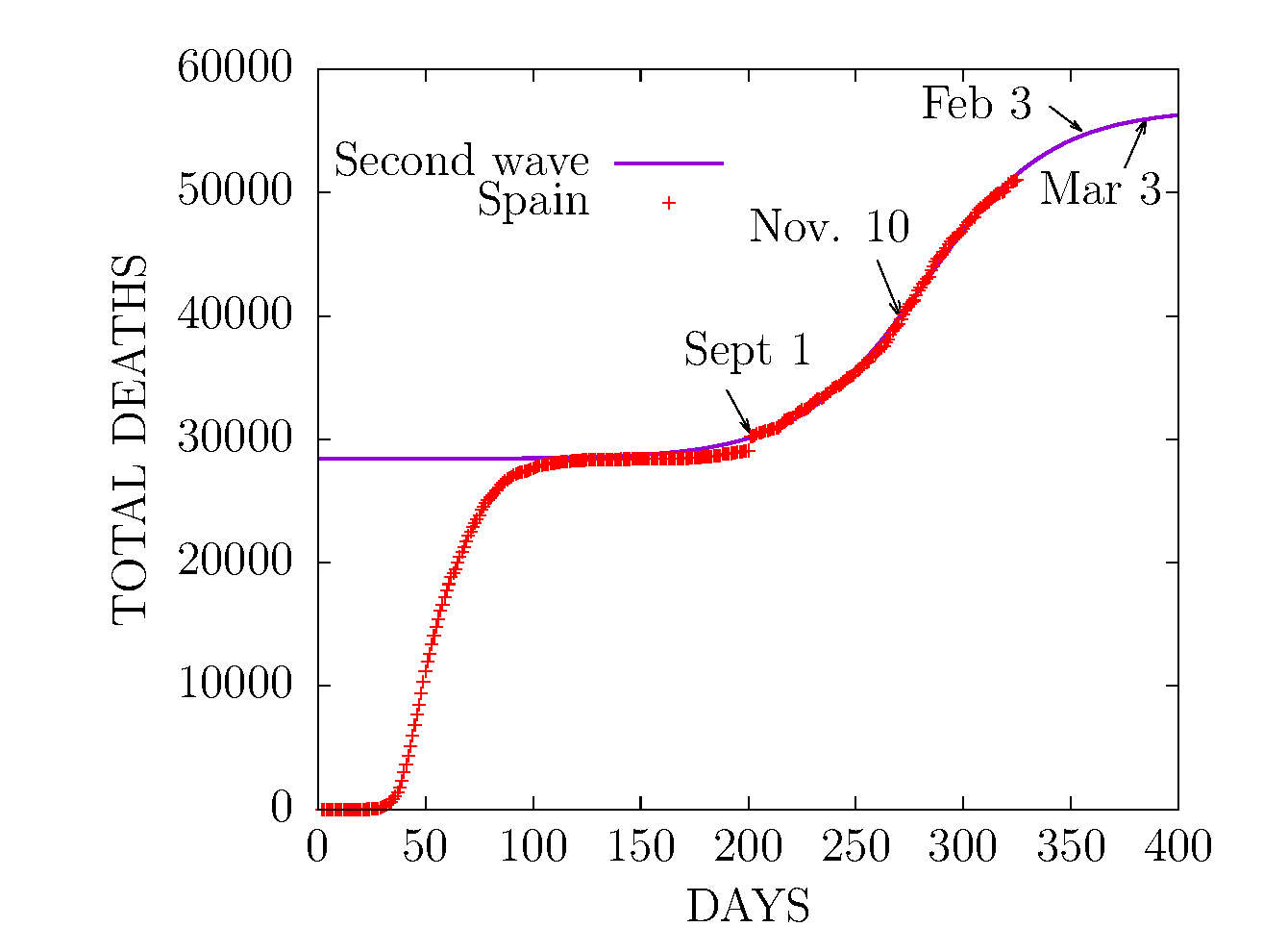
D MODEL - SECOND WAVE IN SPAIN 4 JANUARY 2021
Total deaths. Fit of the second wave using data starting from September. The top of the curve is expected in MARCH 2021.
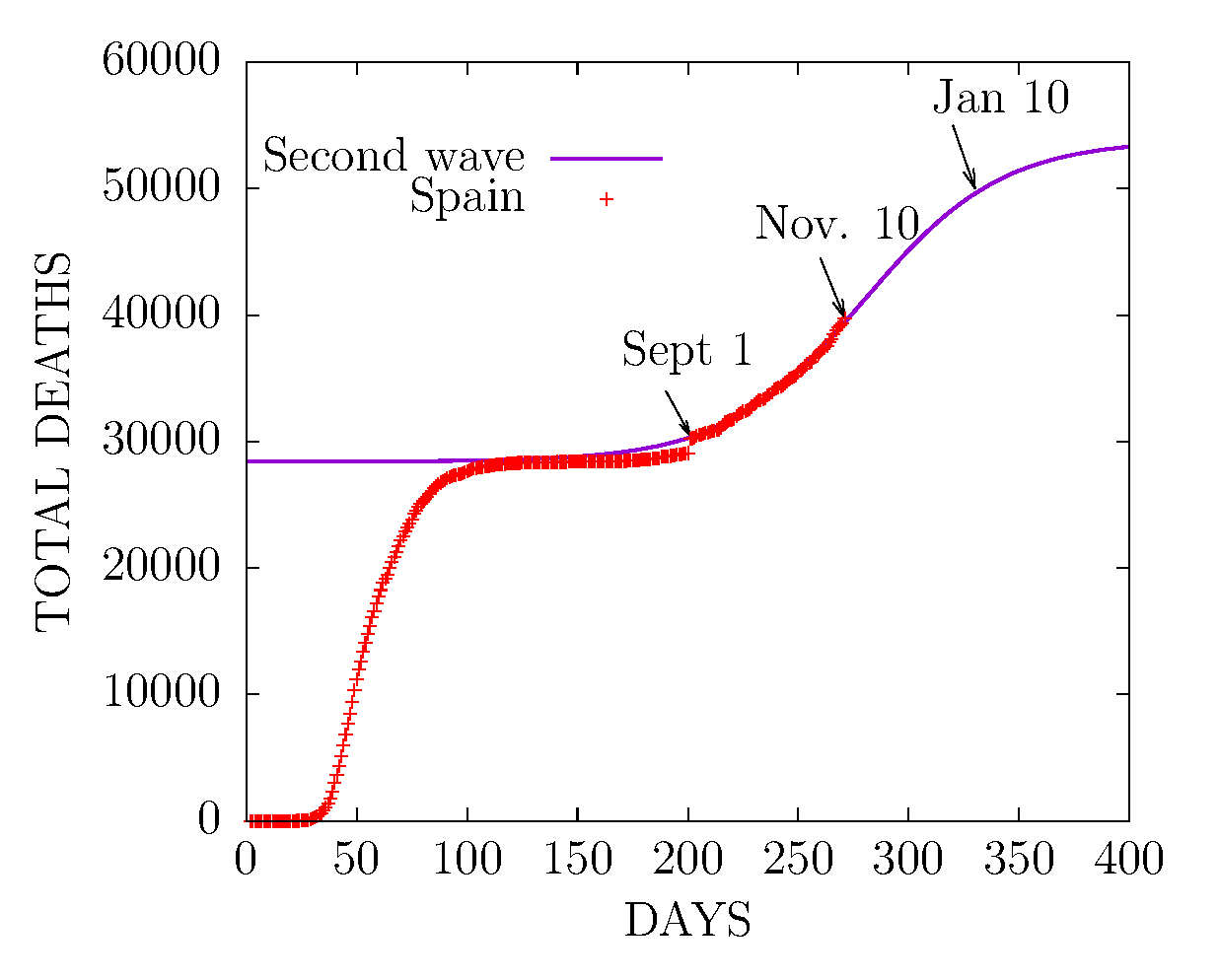
D MODEL - SECOND WAVE IN SPAIN 11 NOVEMBER 2020
Total deaths. Fit of the second wave using data starting from September. The top of the curve is expected in February 2021.
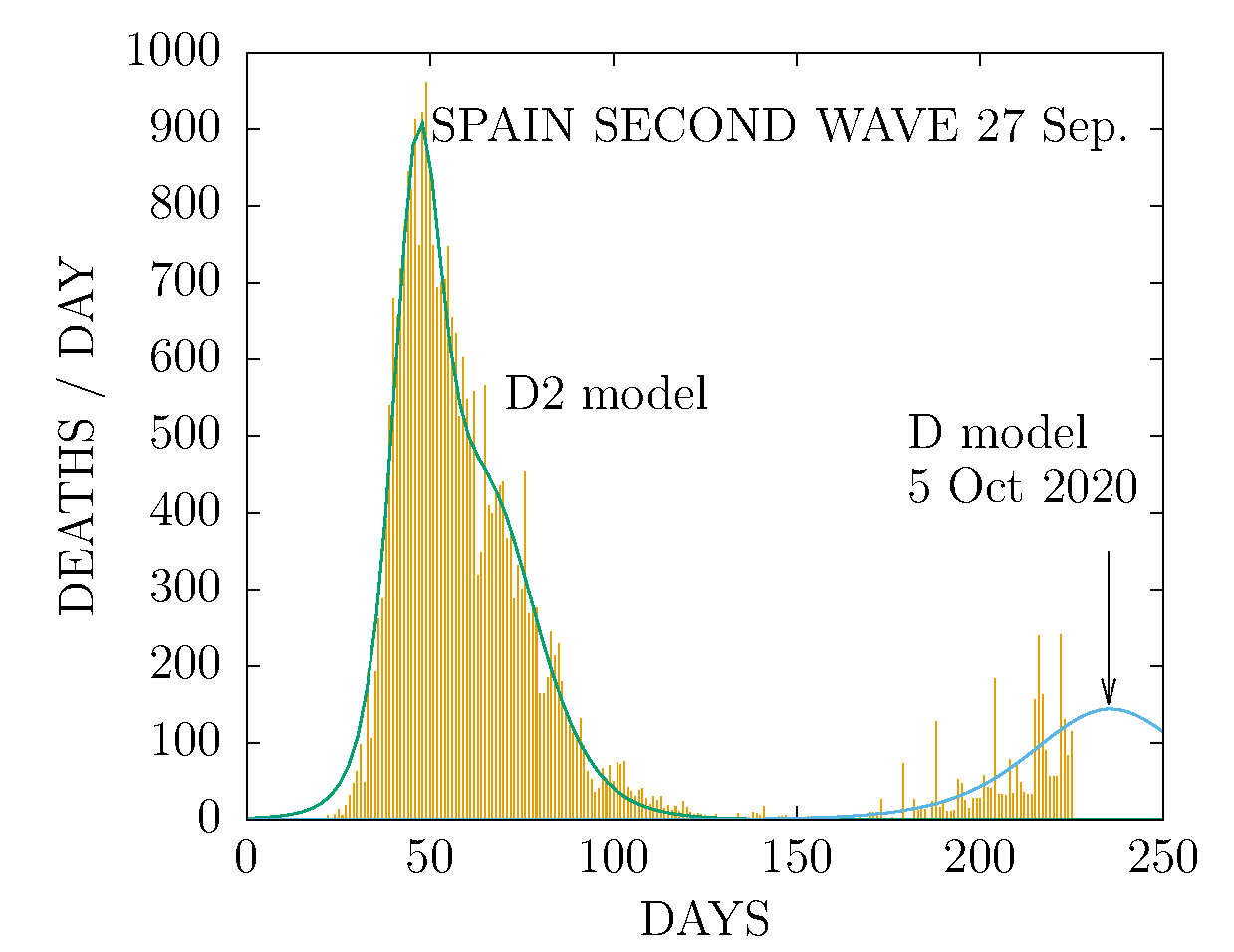
D MODEL - SECOND WAVE IN SPAIN 27 SEPTEMBER
Deaths per day. Fit of the second peak using data starting from July. The maximum is expected in the first weak of Octobrer.
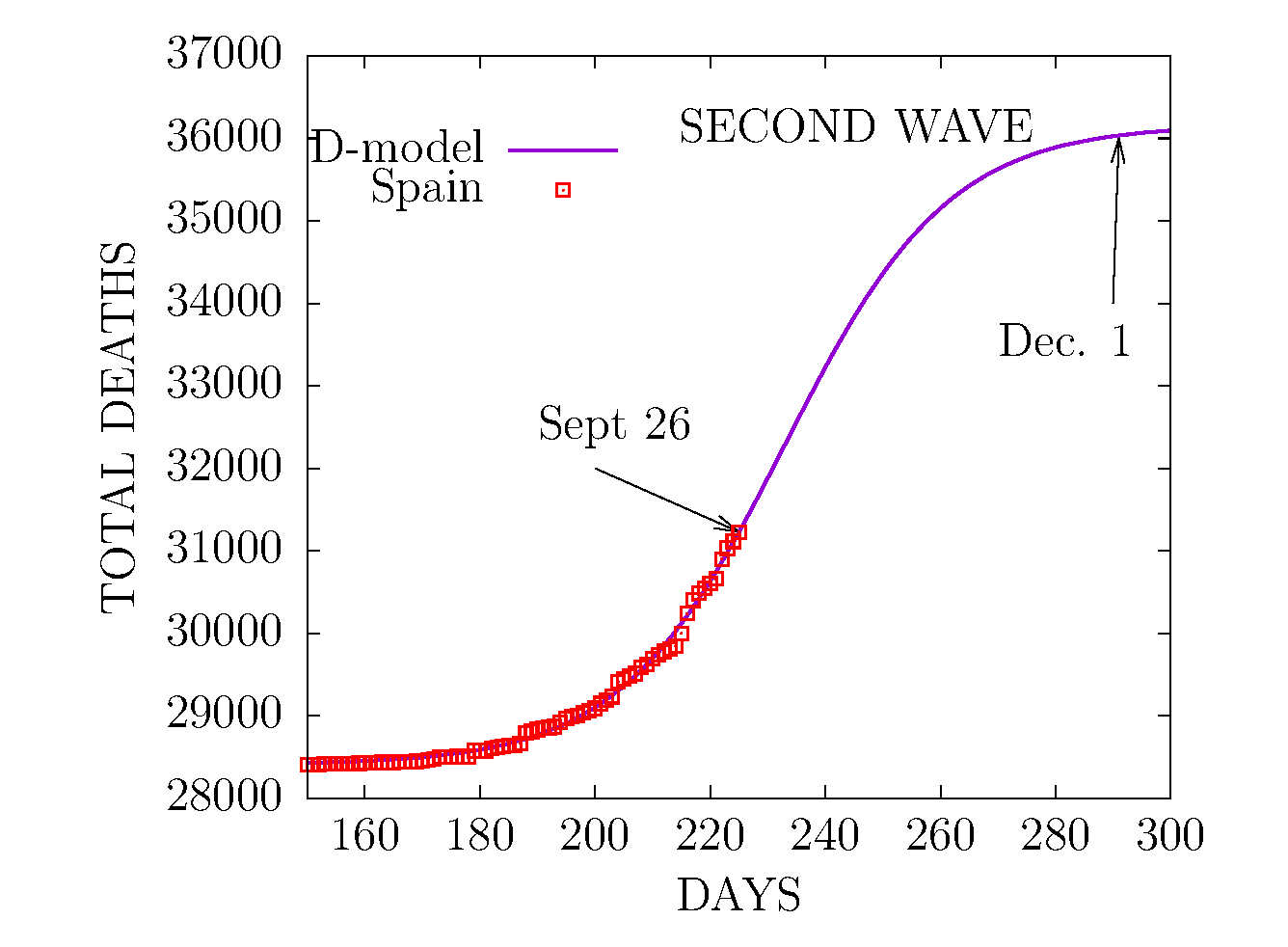
D MODEL - SECOND WAVE IN SPAIN 27 SEPTEMBER
Total deaths. Fit of the second wave using data starting from July. The top of the curve is expected in the first weak of December.
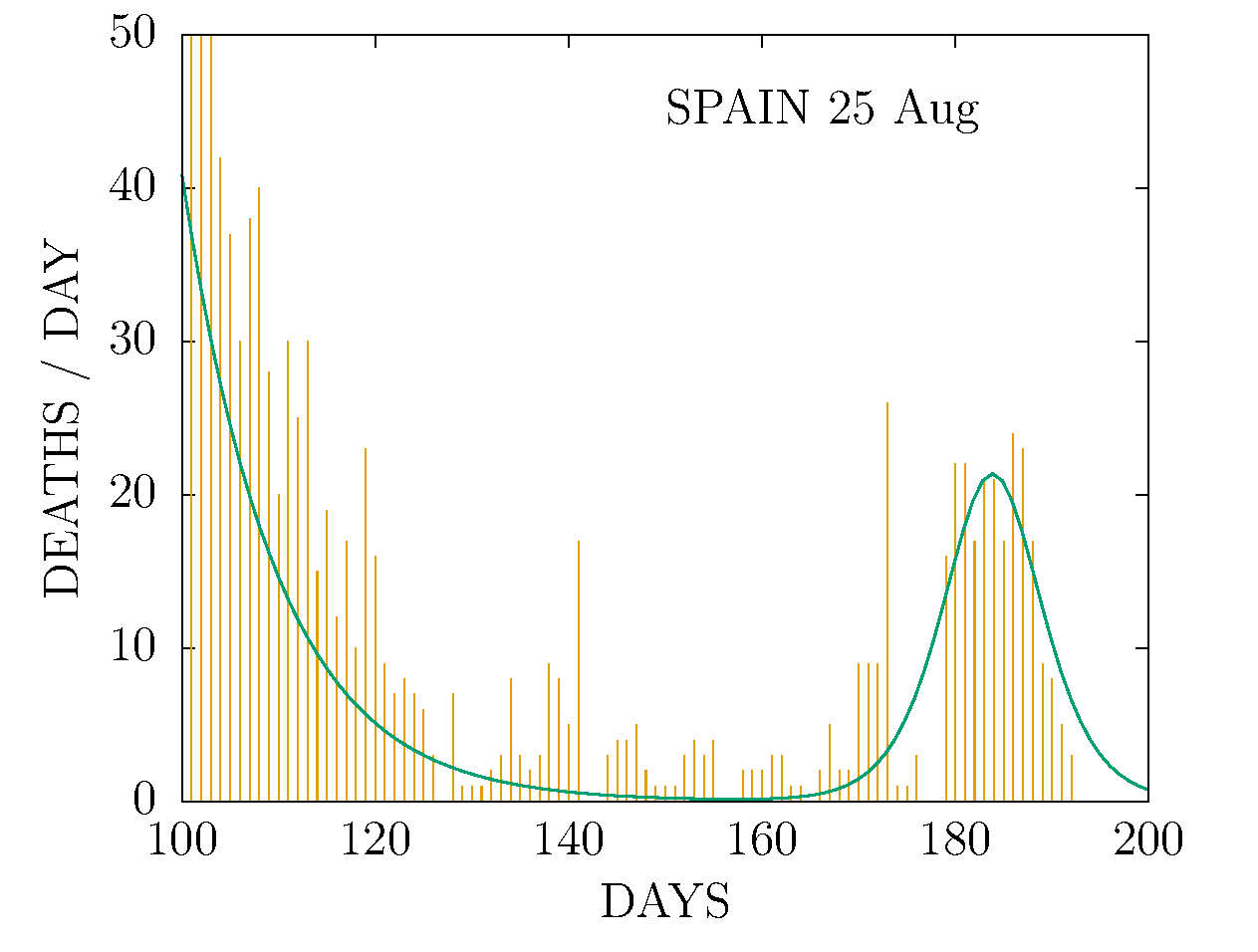
D MODEL - DEATHS-PER-DAY IN SPAIN 25 AUGUST
Detail of the second peak, probably noise.
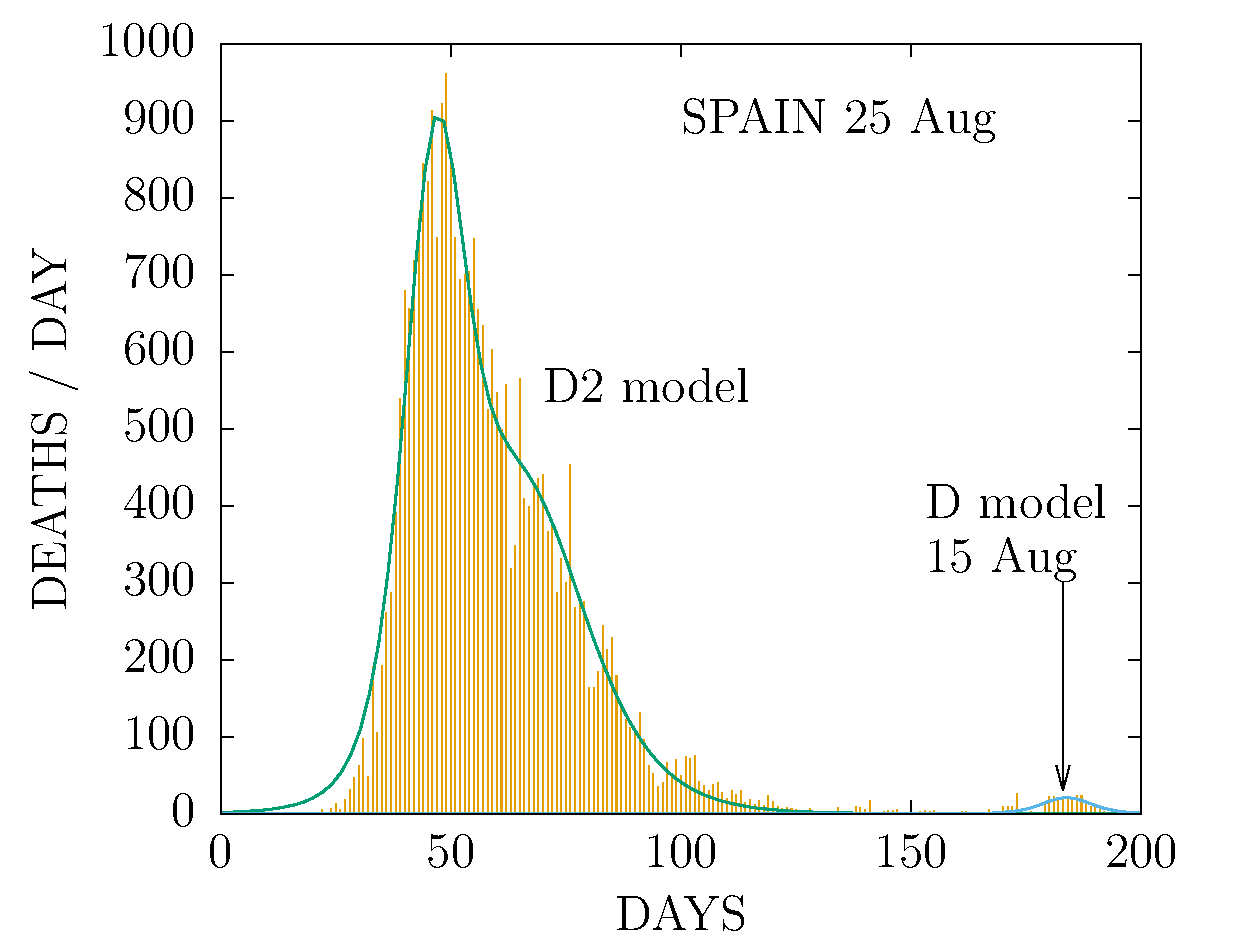
D MODEL - DEATHS-PER-DAY IN SPAIN 25 AUGUST
Second fit of the pandemic regrowth in Spain. The D model has been fitted to the data from July 12. After revision of data from the ministery a much smaller pandemic peak is found with maximum 15 August. This is compatible with noise.
El pico del pretendido rebrote se ha quedado en un pulso estadisticamente poco significativo, pero no corresponde a ninguna pandemia.
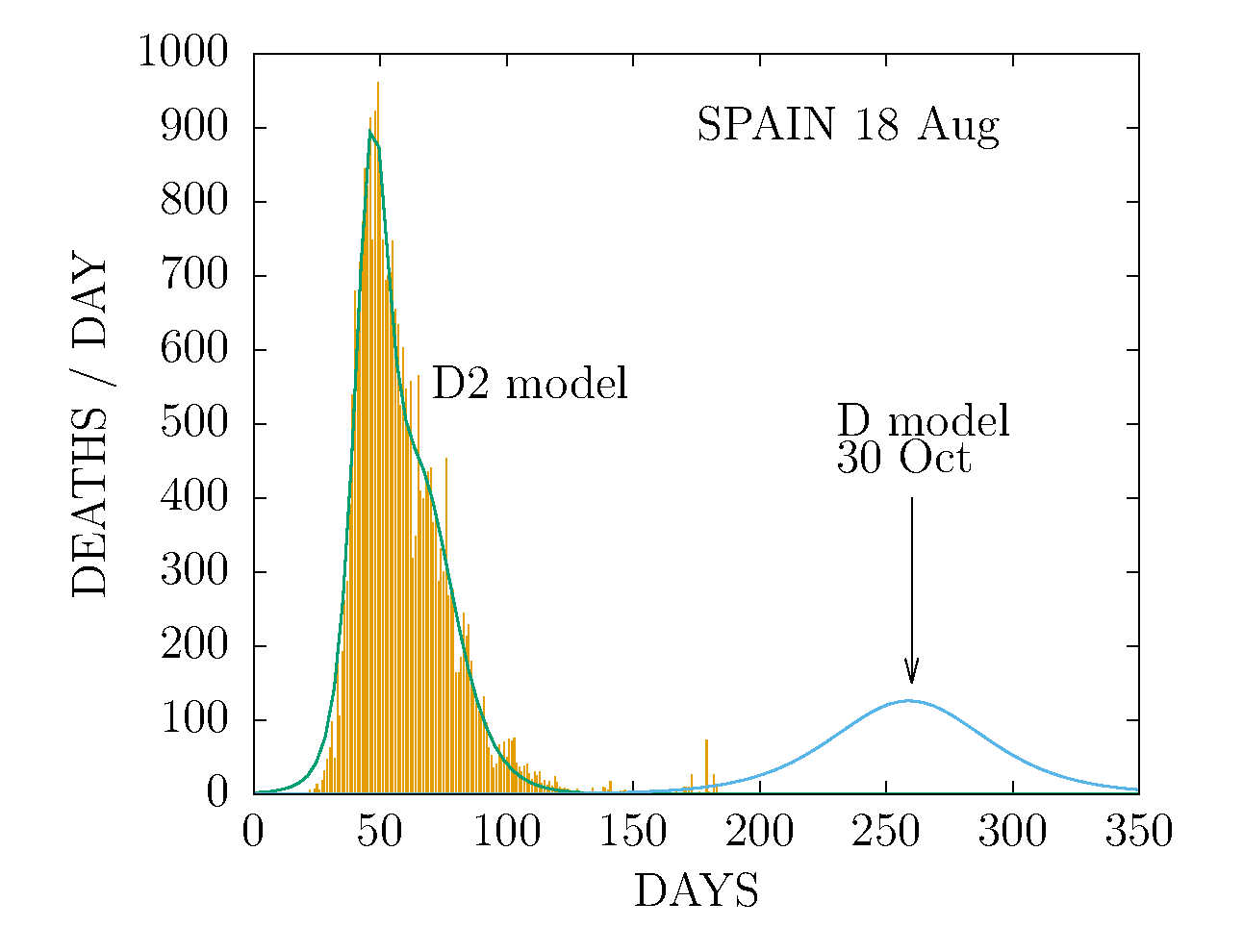
D MODEL - DEATHS-PER-DAY IN SPAIN 18 AUGUST
First prediction of the pandemic regrowth in Spain. The D model has been fitted to the data from July 12. A new pandemic peak is found with maximum 30 October and ending on 30 January. The results are orientative and are expected to change as more data are added to the model.
Primera predicción del rebrote en España. Hemos ajustado el modelo D a los datos disponibles desde el 12 de julio. Encontramos un nuevo pico que alcanza el máximo el 30 de octubre y que habrá desaparecido el 30 de enero. Los resultados son orientativos e irán cambiando a medida que adjuntemos nuevos datos al modelo.
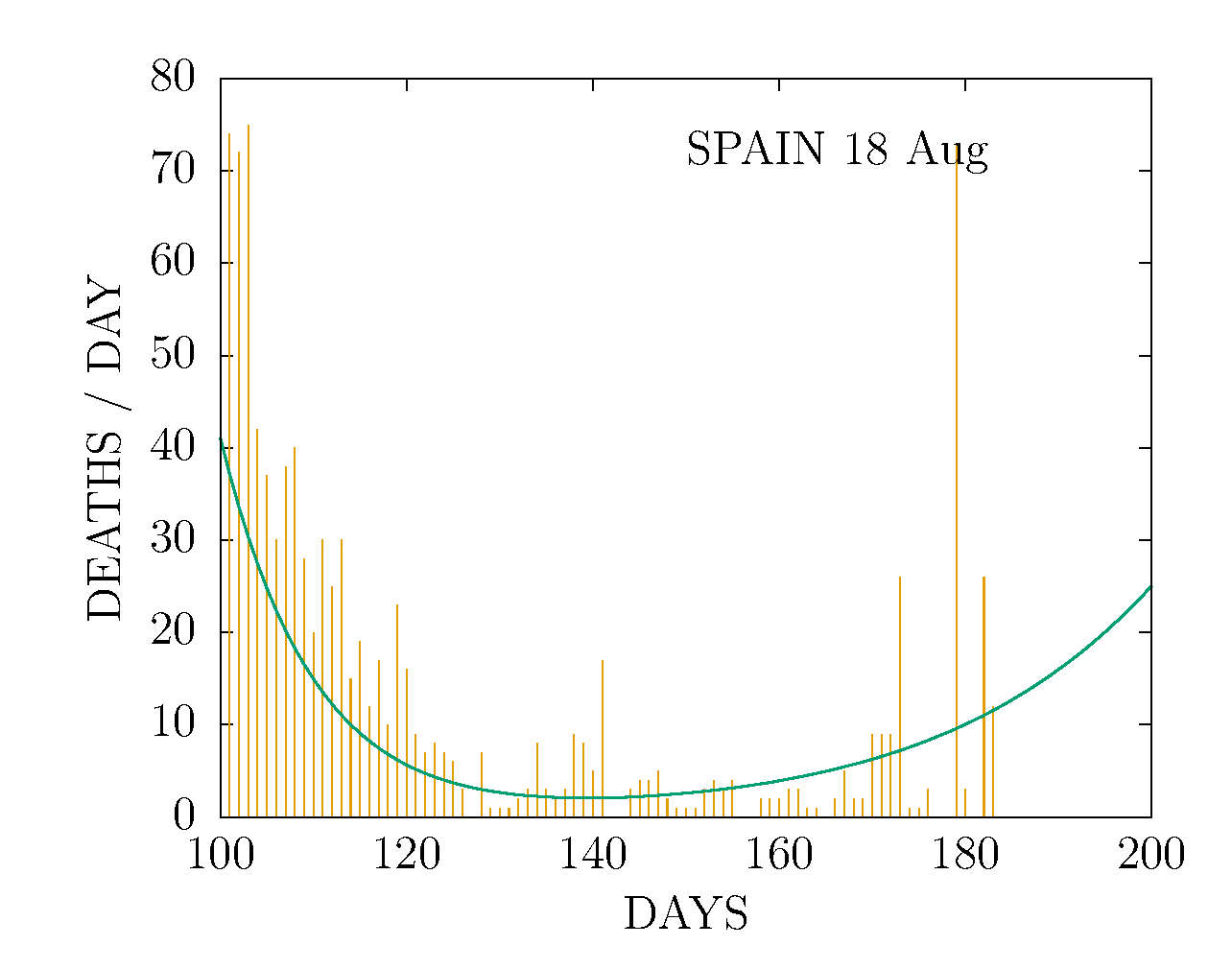
D MODEL - DETAIL DEATHS-PER-DAY IN SPAIN 18 AUGUST
First prediction of the pandemic regrowth in Spain. The D model has been fitted to the data from July 12. A new pandemic peak is found with maximum 30 October and ending on 30 January. The results are orientative and are expected to change as more data are added to the model.
Primera predicción del rebrote en España. Hemos ajustado el modelo D a los datos disponibles desde el 12 de julio. Encontramos un nuevo pico que alcanza el máximo el 30 de octubre y que habrá desaparecido el 30 de enero. Los resultados son orientativos e irán cambiando a medida que adjuntemos nuevos datos al modelo.
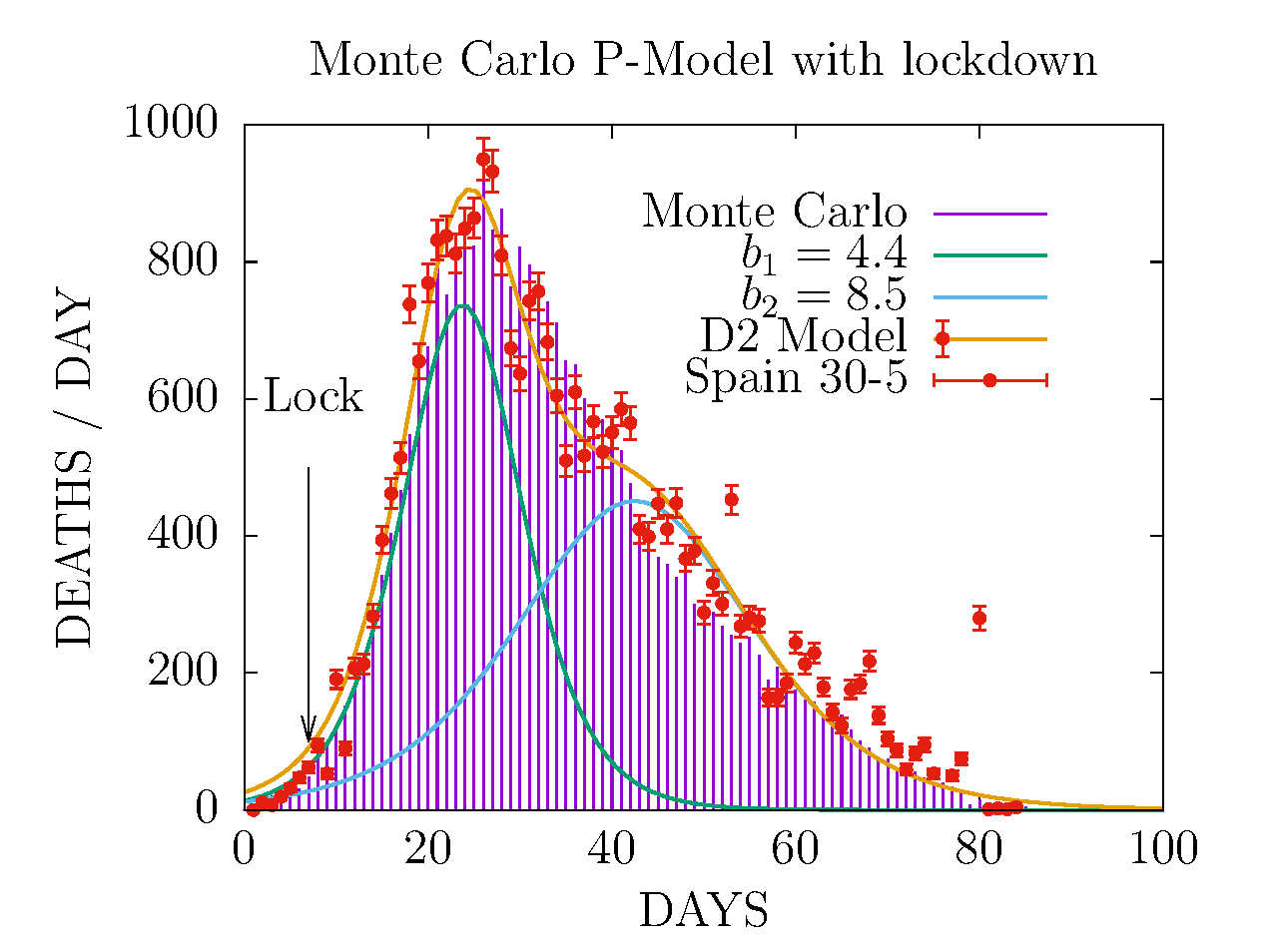
MODEL D2 AND MONTE CARLO - DEATHS-PER-DAY IN SPAIN 30 MAY
This Monte Carlo was fitted to data up to May 2. The end of the pandemic, around May 25, was well reproduced.
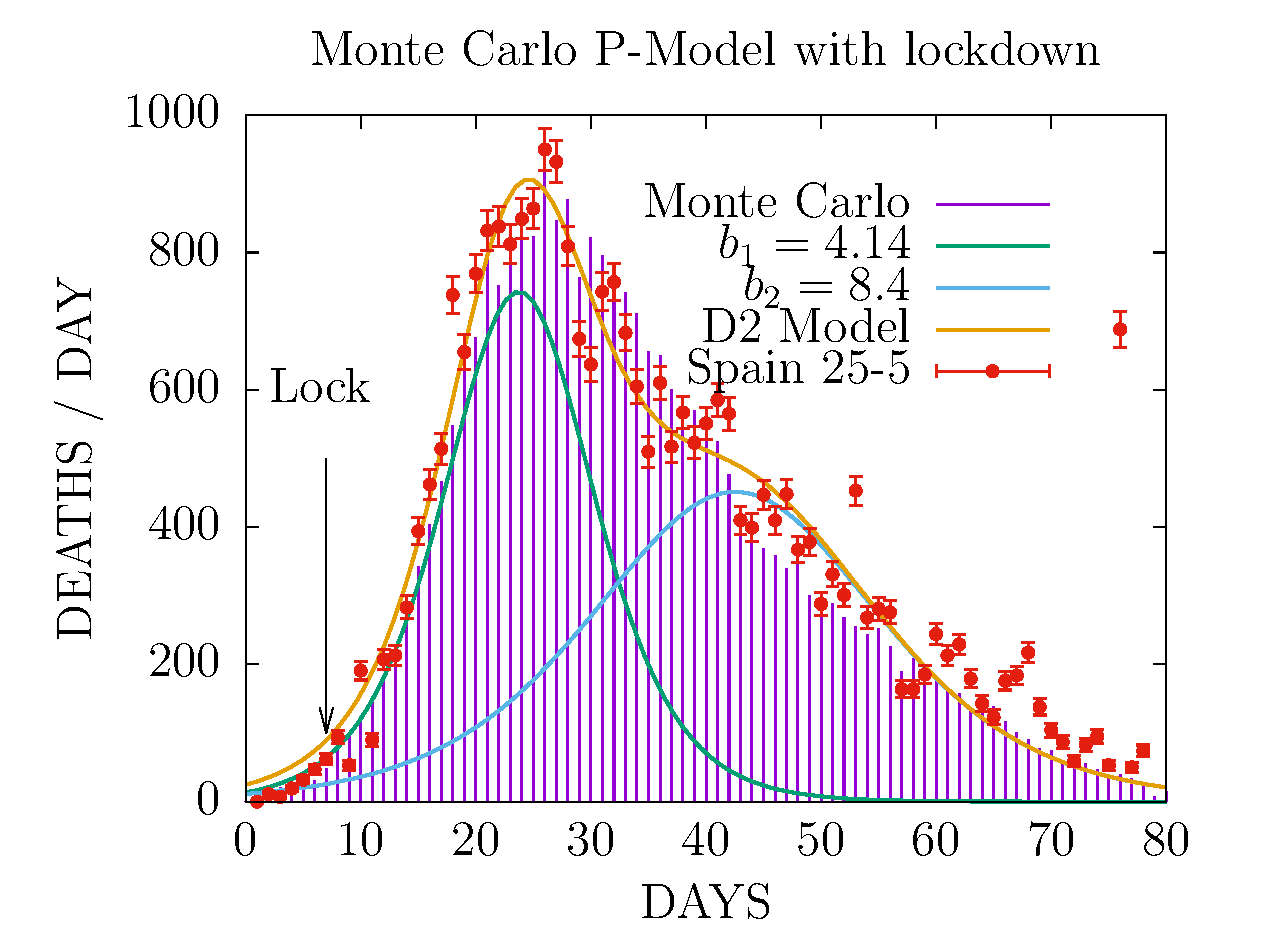
MODEL D2 AND MONTE CARLO - DEATHS-PER-DAY IN SPAIN 25 MAY
This Monte Carlo was fitted to data up to May 2. The end of the pandemic, around May 25, was well reproduced