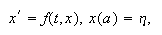 donde
donde
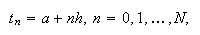 con
con
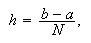 siendo
siendo En muy pocos casos se puede encontrar la solución exacta de un problema de valores iniciales (p.v.i.) y, por tanto, es imprescindible establecer métodos aproximados de cálculo, entre los que se encuentran los basados en desarrollos en serie de potencias, en serie de Frobenius, etc, además de una categoría diferente formada por métodos numéricos.
Consideremos el problema de valores iniciales (p.v.i.) 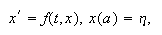 donde
donde
![]() ,
, ![]() y
y ![]() es continua en el dominio
es continua en el dominio
![]() , además de satisfacer
una condición de Lipschitz respecto de
, además de satisfacer
una condición de Lipschitz respecto de ![]() con constante
con constante ![]() , y
, y ![]() . Sea
. Sea ![]() la única solución de (c15:pvi1) y sea
la única solución de (c15:pvi1) y sea ![]() tal que
tal que ![]() . Los métodos numéricos se
basan en la idea de discretización, es decir, en
determinar valores aproximados de
. Los métodos numéricos se
basan en la idea de discretización, es decir, en
determinar valores aproximados de ![]() en el conjunto de nodos
en el conjunto de nodos ![]() definidos por
definidos por 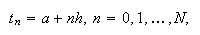 con
con
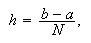 siendo
siendo ![]() dado.
La longitud de paso
dado.
La longitud de paso ![]() determina la partición de
determina la partición de
![]() .
Si
.
Si ![]() ,
, ![]() ,
, ![]() ,
, ![]() son
aproximaciones de
son
aproximaciones de ![]() ,
, ![]() ,
, ![]() ,
, ![]() , respectivamente,
, respectivamente, ![]() es una solución numérica del p.v.i. (c15:pvi1).
es una solución numérica del p.v.i. (c15:pvi1).
Las hipótesis sobre ![]() se mantendrán mientras no se
especifique otra cosa y no se hará en lo sucesivo referencia explícita a las
mismas.
se mantendrán mientras no se
especifique otra cosa y no se hará en lo sucesivo referencia explícita a las
mismas.
Los resultados establecidos sobre derivación e integración numéricas hacen
posible construir diferentes métodos de generación de soluciones numéricas.
Desarrollaremos algunos ejemplos, para lo que supondremos que ![]() .
.
Si la solución ![]() fuese de clase dos,
entonces, por la fórmula de Taylor con resto de Lagrange, se puede escribir
fuese de clase dos,
entonces, por la fórmula de Taylor con resto de Lagrange, se puede escribir
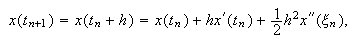 donde
donde ![]() . Como
. Como
![]() es solución de la
ecuación diferencial, la igualdad (c15:euler1) se
transforma en
es solución de la
ecuación diferencial, la igualdad (c15:euler1) se
transforma en 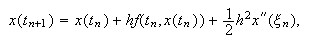 igualdad cierta para
igualdad cierta para ![]() . El
método de Euler, o de Euler-Cauchy,
consiste en aproximar los valores
. El
método de Euler, o de Euler-Cauchy,
consiste en aproximar los valores ![]() mediante los
mediante los ![]() generados por el
siguiente procedimiento:
generados por el
siguiente procedimiento:  Su relación con el método de las
poligonales de Euler es evidente.
Su relación con el método de las
poligonales de Euler es evidente.
?`Qué sucede si ![]() es de clase
es de clase ![]() ? Aplicando la fórmula de
Taylor de orden
? Aplicando la fórmula de
Taylor de orden ![]() con resto de Lagrange
obtenemos que
con resto de Lagrange
obtenemos que 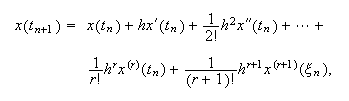 siendo
siendo ![]() un valor en
un valor en
![]() .
.
Como ![]() es
solución del p.v.i., se cumple que
es
solución del p.v.i., se cumple que 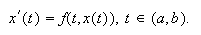 Si utilizamos la notación
Si utilizamos la notación 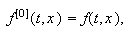 podemos
escribir
podemos
escribir 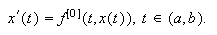 Por tanto,
Por tanto, 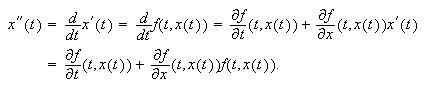 y, si notamos
y, si notamos  entonces
entonces 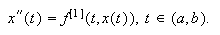 Análogamente,
Análogamente, 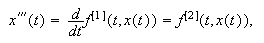 donde
donde
 En general, para
En general, para ![]() , se verifica que
, se verifica que 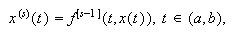 con
con
 Entonces, definiendo
Entonces, definiendo 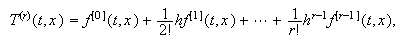 la igualdad (c15:taylor1) da lugar a
la igualdad (c15:taylor1) da lugar a 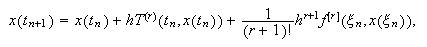 igualdad que sugiere generar las
aproximaciones
igualdad que sugiere generar las
aproximaciones ![]() de
de ![]() por medio del siguiente
procedimiento:
por medio del siguiente
procedimiento: 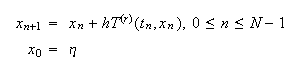 Lo denominaremos método de Taylor de orden
Lo denominaremos método de Taylor de orden ![]() .
.
Observemos que presenta un gran inconveniente, a saber, que hay que calcular
cierto número de derivadas sucesivas de la solución del p.v.i. Sería, pues,
conveniente desarrollar un procedimiento que produjese un error similar al que
aparece en (c15:taylor1), pero que evitase calcular las
derivadas de la solución del p.v.i. Por simplicidad, y dado que sólo estamos
presentando algunos ejemplos concretos, supongamos ![]() . Entonces, (c15:taylor1) se escribe como
. Entonces, (c15:taylor1) se escribe como 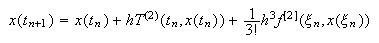 donde
donde 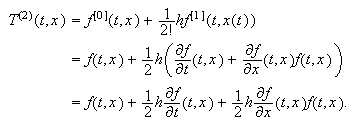
Sean ![]() y
y
![]() valores que
determinaremos a posteriori. Hallemos el polinomio de
Taylor de orden uno de la función
valores que
determinaremos a posteriori. Hallemos el polinomio de
Taylor de orden uno de la función ![]() alrededor de
alrededor de ![]() .
Teniendo en cuenta que
.
Teniendo en cuenta que 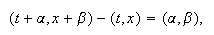 podemos escribir
podemos escribir 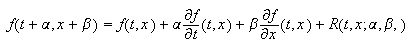 con
con
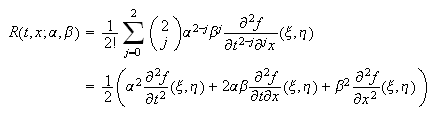 donde
donde ![]() es un
valor entre
es un
valor entre ![]() y
y ![]() y
y ![]() uno entre
uno entre ![]() y
y ![]() .
.
Fijémonos en las expresiones para ![]() y
y ![]() . Si
. Si ![]() y
y
![]() , entonces
, entonces  por lo
que
por lo
que 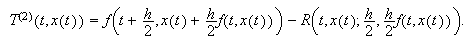 En consecuencia,
En consecuencia, 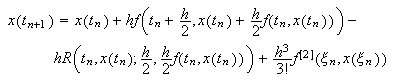 donde
donde
![]() .
.
Podemos, por tanto, generar una solución numérica de (c15:pvi1) por medio del siguiente esquema: 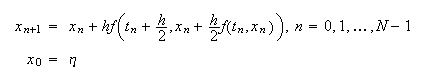 Es el
método de Euler corregido. Para calcular
Es el
método de Euler corregido. Para calcular ![]() a partir de
a partir de
![]() hay que evaluar
dos veces la función
hay que evaluar
dos veces la función ![]() .
.
Hemos visto cómo la técnica empleada para establecer el método de Euler puede seguirse para encontrar los métodos de Taylor y cómo es posible, al menos en el caso que hemos desarrollado, producir un método con un error similar pero para el que no hay que calcular derivadas.
Vamos a proceder de un modo totalmente diferente para establecer otro método para generar una solución numérica.
De nuevo, sea ![]() la única solución del p.v.i
(c15:pvi1). Consideremos un subintervalo cualquiera
la única solución del p.v.i
(c15:pvi1). Consideremos un subintervalo cualquiera ![]() . Como
. Como ![]() para
para ![]() , se cumple que
, se cumple que  es
decir,
es
decir, 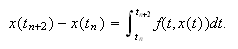 Consideremos ahora la función
Consideremos ahora la función ![]()
![]() , que no es conocida
al no disponer de
, que no es conocida
al no disponer de ![]() . La fórmula de Simpson
permite escribir
. La fórmula de Simpson
permite escribir 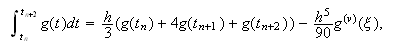 por lo que
por lo que 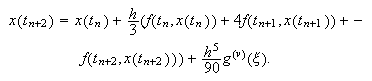 Es
razonable generar una solución numérica del p.v.i. (c15:pvi1) mediante el siguiente procedimiento, en que se usa la
notación
Es
razonable generar una solución numérica del p.v.i. (c15:pvi1) mediante el siguiente procedimiento, en que se usa la
notación ![]() :
:  Es el
denominado método de Simpson.
Es el
denominado método de Simpson.
Claramente, en los métodos de Euler, Taylor y Euler corregido que hemos
desarrollado el cálculo del término ![]() de la solución numérica se
basa en el conocimiento del
de la solución numérica se
basa en el conocimiento del ![]() ; la sucesión
; la sucesión ![]() se calcula secuencialmente
a partir
se calcula secuencialmente
a partir ![]() ,
haciendo
,
haciendo ![]() en las ecuaciones en diferencias de
(c15:euler2), (c15:taylor2) y
(c15:eulercorregido), respectivamente. En el método de
Simpson (c15:simpson) el término
en las ecuaciones en diferencias de
(c15:euler2), (c15:taylor2) y
(c15:eulercorregido), respectivamente. En el método de
Simpson (c15:simpson) el término ![]() de la
solución numérica se calcula a partir de los dos precedentes, por lo que será
necesario proporcionar un valor inicial adicional,
de la
solución numérica se calcula a partir de los dos precedentes, por lo que será
necesario proporcionar un valor inicial adicional, ![]() , antes de que
la sucesión
, antes de que
la sucesión ![]() pueda
ser calculada.
pueda
ser calculada.
Si el método es tal que, dados ![]() ,
, ![]() , se
determina
, se
determina ![]() explícitamente, el método se dice explícito; éste es el
caso de los métodos de Euler, Taylor y Euler corregido que hemos considerado.
Si, por el contrario, el valor
explícitamente, el método se dice explícito; éste es el
caso de los métodos de Euler, Taylor y Euler corregido que hemos considerado.
Si, por el contrario, el valor ![]() no puede ser calculado sin
resolver un sistema de ecuaciones implícito, como es el caso del método de
Simpson, entonces el método se dice implícito. Como la
función
no puede ser calculado sin
resolver un sistema de ecuaciones implícito, como es el caso del método de
Simpson, entonces el método se dice implícito. Como la
función ![]() es, en
general, no lineal en
es, en
general, no lineal en ![]() , en los métodos implícitos
hay que considerar la resolución de un sistema no lineal de ecuaciones en cada
paso de los cálculos, y son, por tanto, computacionalmente más costosos que los
métodos explícitos. Observemos, por último, que en la ecuación en diferencias
para el método de Simpson intervienen sólo combinaciones lineales de
, en los métodos implícitos
hay que considerar la resolución de un sistema no lineal de ecuaciones en cada
paso de los cálculos, y son, por tanto, computacionalmente más costosos que los
métodos explícitos. Observemos, por último, que en la ecuación en diferencias
para el método de Simpson intervienen sólo combinaciones lineales de ![]() ,
, ![]() ,
, ![]() .
.
Los métodos desarrollados, salvo los de Taylor, son aplicables para resolver
p.v.i. correspondientes a sistemas diferenciales, es decir, en el caso ![]() .
.
Tras considerar algunos métodos específicos, es hora de precisar la noción de
método numérico, para lo que debemos tener en cuenta cómo en aquéllos cada
término de la solución numérica se calcula a partir de algún subconjunto ![]() ,
, ![]() ,
, ![]() ,
, ![]() de valores
calculados, lo que implica conocer
de valores
calculados, lo que implica conocer ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Adoptamos el
procedimiento seguido en [Stetter], adonde remitimos para las demostraciones de
los resultados que se especificarán..
. Adoptamos el
procedimiento seguido en [Stetter], adonde remitimos para las demostraciones de
los resultados que se especificarán..
Un método numérico de ![]() pasos para el
p.v.i. (c15:pvi1) está constituido por valores
iniciales
pasos para el
p.v.i. (c15:pvi1) está constituido por valores
iniciales 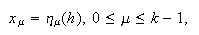 y una ecuación en
diferencias de la forma
y una ecuación en
diferencias de la forma 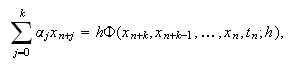 donde
donde ![]() ,
,
![]() ,
,
![]() ,
, ![]() son
números reales y
son
números reales y ![]() una función -dependiente
de
una función -dependiente
de ![]() y
y ![]() - definida en un
subconjunto de
- definida en un
subconjunto de ![]() que verifica las
siguientes propiedades:
que verifica las
siguientes propiedades:
Si ![]() entonces
entonces ![]() .
.
Existe una constante ![]() tal que
tal que 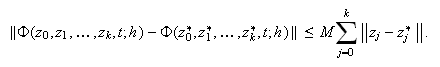
Si ![]() aparece en
aparece en ![]() el método (c15:pvi3) se dice implícito, y explícito en caso contrario.
el método (c15:pvi3) se dice implícito, y explícito en caso contrario.
Por ejemplo, para el método de Euler 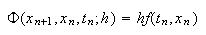 y
y 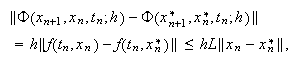 por lo que basta con tomar
por lo que basta con tomar
![]() .
.
Para el método de Simpson, 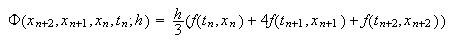 y
y 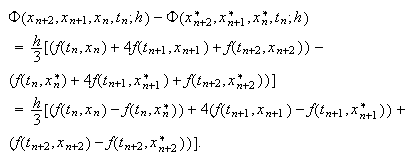 Por tanto,
Por tanto, 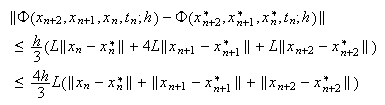 y
podemos tomar
y
podemos tomar ![]() .
.
Finalmente, para el método de Euler corregido, 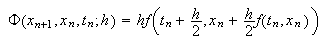 y
y 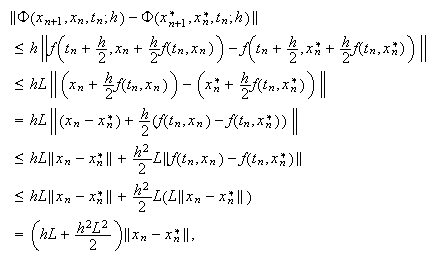 de
donde se deduce que, por ejemplo,
de
donde se deduce que, por ejemplo, ![]() .
.
Nótese que sólo hemos utilizado el que ![]() satisface, por hipótesis,
una condición de Lipschitz respecto de
satisface, por hipótesis,
una condición de Lipschitz respecto de ![]() y la desigualdad triangular
para la norma
y la desigualdad triangular
para la norma ![]() , que es
arbitraria.
, que es
arbitraria.
El método (c15:pvi2 )-(c15:pvi3) debe comportarse bien cuando
![]() tiende a cero para
ser útil.
tiende a cero para
ser útil.
Diremos que (c15:pvi2 )-(c15:pvi3) es un método convergente si para todos los
p.v.i. (c15:pvi1) y cualesquiera condiciones iniciales
(c15:pvi2) para las que 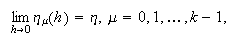 se cumple que
se cumple que 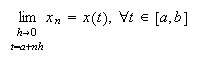 para
todas las soluciones numéricas
para
todas las soluciones numéricas ![]() generadas por aquél. Un
método que no es convergente se dice divergente.
generadas por aquél. Un
método que no es convergente se dice divergente.
Frecuentemente se toma como definición de convergencia el que 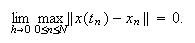 Es
equivalente, pero no se aprecia en ella la necesidad de considerar límite para
Es
equivalente, pero no se aprecia en ella la necesidad de considerar límite para
![]() con
con
![]() fijo.
fijo.
Si el método es convergente los errores globales ![]() tienden a cero.
tienden a cero.
Determinar la convergencia de un método numérico no es fácil, por lo que es importante disponer de criterios que la garanticen.
Se define el error de truncatura local ![]() como
como 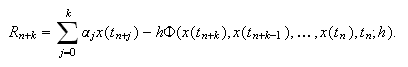
Mide si el método (c15:pvi3) es una representación lo suficientemente exacta del sistema diferencial de (c15:pvi1).
El método (c15:pvi3) se dice
consistente (con el sistema diferencial de (c15:pvi1)) si para todos los p.v.i. (c15:pvi1) se cumple que 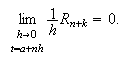
La consistencia se expresa en términos de ![]() ,
, ![]() y
y ![]() ,
, ![]() .
.
El método (c15:pvi3) es consistente si
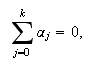
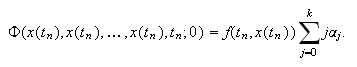
Definimos el primer polinomio característico
![]() del método
(c15:pvi3) como
del método
(c15:pvi3) como 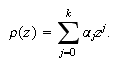
La condición (c15:pvi4) equivale a ![]() y (c15:pvi5) a
y (c15:pvi5) a 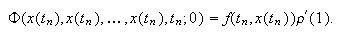
La convergencia de un método implica su consistencia. El recíproco no es
cierto: el método puede ser muy sensible a las perturbaciones de ![]() y
y ![]() . La perturbación
. La perturbación ![]() y la solución perturbada
y la solución perturbada ![]() del método (c15:pvi2 )-(c15:pvi3) se definen por
medio de las igualdades
del método (c15:pvi2 )-(c15:pvi3) se definen por
medio de las igualdades 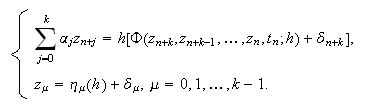
Sean ![]() y
y ![]() cualesquiera dos
perturbaciones de (c15:pvi2 )-(c15:pvi3), y sean
cualesquiera dos
perturbaciones de (c15:pvi2 )-(c15:pvi3), y sean ![]() y
y ![]() sus respectivas
soluciones perturbadas. Se dice que el método (c15:pvi3) es cero-estable si existen constantes
sus respectivas
soluciones perturbadas. Se dice que el método (c15:pvi3) es cero-estable si existen constantes
![]() y
y ![]() tales que,
para todo
tales que,
para todo ![]() , se
cumple que
, se
cumple que 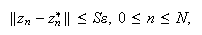 cuando
cuando 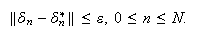
La cero-estabilidad se refiere al comportamiento del método en lo que
respecta a las perturbaciones cuando ![]() tiende a cero, y es una
propiedad del método. Los errores debidos a la discretización pueden
considerarse perturbaciones, así como los errores de redondeo.
tiende a cero, y es una
propiedad del método. Los errores debidos a la discretización pueden
considerarse perturbaciones, así como los errores de redondeo.
?`Cuándo se da la cero-estabilidad?
El método (c15:pvi2 )-(c15:pvi3) es cero-estable si y sólo si todas las raíces del primer polinomio característico tengan módulo menor o igual que la unidad, y que las de módulo unidad sean simples.
Los conceptos de convergencia, consistencia y cero-estabilidad se relacionan del siguiente modo:
El método (c15:pvi3) es convergente si y sólo si es consistente y cero-estable.
Algunos de los métodos enumerados al comienzo comparten una propiedad y es
que ![]() es una
combinación lineal de los valores
es una
combinación lineal de los valores ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Son casos particulares de
una familia de métodos. Emplearemos la notación
. Son casos particulares de
una familia de métodos. Emplearemos la notación ![]() , como ya hicimos
anteriormente.
, como ya hicimos
anteriormente.
Llamaremos método lineal multipaso o método
de ![]() pasos a cualquier método (c15:pvi3) de la
forma
pasos a cualquier método (c15:pvi3) de la
forma 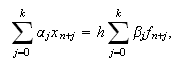 donde
donde ![]() y
y
![]() ,
, ![]() ,
son constantes tales que
,
son constantes tales que ![]() y
y ![]() .
.
El que las estructuras de ambos términos de (c15:mmp1)
sean iguales sugiere definir un polinomio similar a ![]() .
.
Se define el segundo polinomio característico de
(c15:mmp1) como 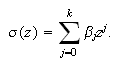
Si ![]() el método es implícito y la determinación de
el método es implícito y la determinación de ![]() se reduce a
resolver un sistema no lineal de la forma
se reduce a
resolver un sistema no lineal de la forma 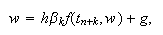 donde
donde ![]() es una expresión conocida
de los valores
es una expresión conocida
de los valores ![]() previamente calculados.
Este sistema tiene una única solución si
previamente calculados.
Este sistema tiene una única solución si ![]() se elige de modo que
se elige de modo que 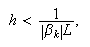 donde
donde
![]() es una constante de
Lipschitz de
es una constante de
Lipschitz de ![]() . La
solución se determina por iteraciones sucesivas.
. La
solución se determina por iteraciones sucesivas.
El error de truncatura local definido en (c15:pvi3bis
) adopta la expresión 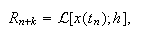 donde
donde 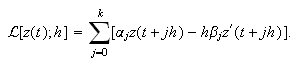 Si
Si ![]() es suficientemente
derivable,
es suficientemente
derivable, 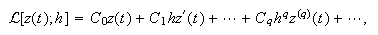 con
con 
El método (c15:mmp1) se dice de
orden ![]() si
si ![]() y
y ![]() . En
este caso,
. En
este caso, ![]() se llama constante de error.
se llama constante de error.
Si el método es de orden ![]() , el error de truncatura
local es del orden
, el error de truncatura
local es del orden ![]() y los errores globales
y los errores globales
![]() . A priori, es
deseable establecer métodos del mayor orden posible, aunque hay limitaciones
ligadas al número de pasos.
. A priori, es
deseable establecer métodos del mayor orden posible, aunque hay limitaciones
ligadas al número de pasos.
Ningún método lineal de ![]() pasos puede tener orden
que exceda el valor
pasos puede tener orden
que exceda el valor ![]() (resp.
(resp. ![]() ) si
) si ![]() es impar (resp. par).
es impar (resp. par).
La integración numérica permite construir métodos lineales multipaso de una
manera sistemática, como ya vimos al establecer el método de Simpson. Una
estrategia consiste en emplear la igualdad 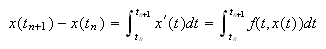 y aproximar numéricamente la
integral de la función
y aproximar numéricamente la
integral de la función ![]() empleando su polinomio de
interpolación en los nodos equidistantes
empleando su polinomio de
interpolación en los nodos equidistantes ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , con
, con ![]() .
.
Los métodos multipaso de la forma 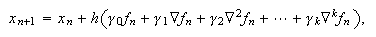 con
con
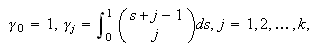 se denominan métodos de
Adams-Bashforth.
se denominan métodos de
Adams-Bashforth.
Son explícitos de ![]() pasos. Se evita el cálculo
individual de las integrales que definen los coeficientes
pasos. Se evita el cálculo
individual de las integrales que definen los coeficientes ![]() ,
, ![]() ,
teniendo en cuenta que
,
teniendo en cuenta que 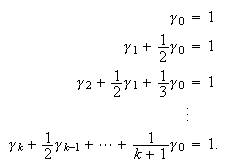
Evidentemente, los métodos (c15:mmp2 )-(c15:mmp3) se pueden reescribir en la forma 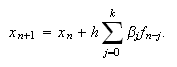
Si a los nodos empleados para establecer la familia de métodos de
Adams-Bashforth añadimos ![]() surge una nueva familia de
métodos multipaso.
surge una nueva familia de
métodos multipaso.
Los métodos multipaso de la forma 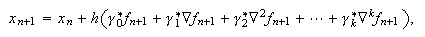 con
con
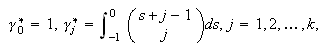 se denominan métodos de
Adams-Moulton.
se denominan métodos de
Adams-Moulton.
Son implícitos de ![]() pasos. Los coeficientes
pasos. Los coeficientes
![]() ,
, ![]() , se
hallan a través de la relación
, se
hallan a través de la relación 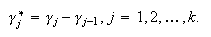
Los métodos de Adams-Bashforth y Adams-Moulton adoptan expresiones del tipo
(c15:mmp1) sin más que efectuar los cambios de índice
adecuados. Su primer polinomio característico es ![]() . Son convergentes.
. Son convergentes.
La utilización de la igualdad 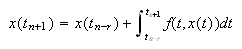 con
con ![]() origina los métodos
explícitos de Nyström
origina los métodos
explícitos de Nyström 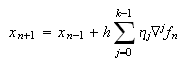 y los implícitos de
Milne-Simpson
y los implícitos de
Milne-Simpson 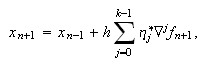 cuyos coeficientes se relacionan con
los
cuyos coeficientes se relacionan con
los ![]() y
y ![]() . Su
primer polinomio característico es
. Su
primer polinomio característico es ![]() . También son convergentes.
. También son convergentes.
Se indicó la suficiencia de la condición ![]() para garantizar la
convergencia del método de las aproximaciones sucesivas para determinar
para garantizar la
convergencia del método de las aproximaciones sucesivas para determinar ![]() del método
(c15:pvi3) cuando es implícito. En el caso del multipaso
del método
(c15:pvi3) cuando es implícito. En el caso del multipaso
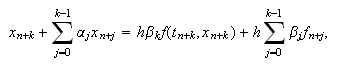 da lugar a la iteración
da lugar a la iteración 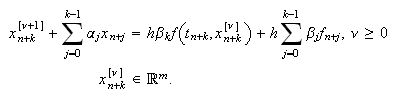 El valor
El valor ![]() , que es arbitrario, puede
ser obtenido a partir de un método multipaso explícito
, que es arbitrario, puede
ser obtenido a partir de un método multipaso explícito 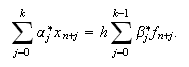
El uso conjunto de los métodos (c15:PrCo1 )-(c15:PrCo2) constituye un método predictor-corrector. Los métodos (c15:PrCo1) y (c15:PrCo2) se eligen del mismo orden y los de tipo Adams constituyen una elección habitual.
Todos los métodos enumerados inicialmente como modelos son lineales multipaso
ya descritos excepto el de Euler corregido. Pertenece a una categoría diferente
de métodos, que se motivan muy bien considerando la versión escalar (![]() ) del problema (c15:pvi1) y haciendo uso del desarrollo de Taylor
) del problema (c15:pvi1) y haciendo uso del desarrollo de Taylor  El
conocimiento de las expresiones exactas de
El
conocimiento de las expresiones exactas de ![]() ,
, ![]() , a partir de
, a partir de
![]() y sus derivadas
sucesivas conduce a los métodos de Taylor
y sus derivadas
sucesivas conduce a los métodos de Taylor 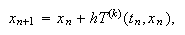 con
con
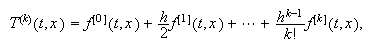 siendo
siendo 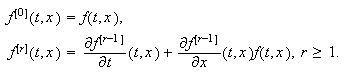 Son métodos de un paso, convergentes
si se hacen las hipótesis oportunas sobre la lipschitzianidad de
Son métodos de un paso, convergentes
si se hacen las hipótesis oportunas sobre la lipschitzianidad de ![]() y sus derivadas sucesivas.
El intento de evitar el uso de derivadas sucesivas conduce a los métodos de Runge-Kutta, que responden a la formulación general
(para sistemas diferenciales)
y sus derivadas sucesivas.
El intento de evitar el uso de derivadas sucesivas conduce a los métodos de Runge-Kutta, que responden a la formulación general
(para sistemas diferenciales) 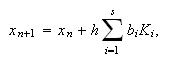 donde
donde 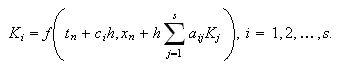 El valor
El valor ![]() indica el número de
evaluaciones de
indica el número de
evaluaciones de ![]() que hay que efectuar.
que hay que efectuar.
La idea subyacente consiste básicamente en considerar ![]() números ordenados del
números ordenados del ![]() al
al ![]() de la forma
de la forma 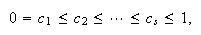 y en
emplear la subdivisión
y en
emplear la subdivisión 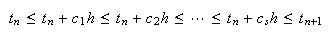 del subintervalo
del subintervalo ![]() . Supondremos que se
verifica la condición
. Supondremos que se
verifica la condición 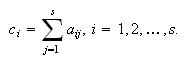
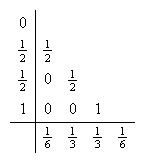
El método de Runge-Kutta (c15:RK1 )-(c15:RK3) se representa por medio de la tabla  Será
un método explícito si
Será
un método explícito si ![]() para
para ![]() ,
, ![]() .
.
Están en la clase de métodos dada por (c15:pvi3), con
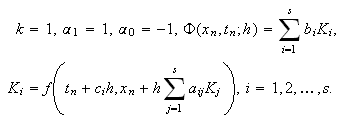 Su convergencia dependerá de su consistencia.
Su convergencia dependerá de su consistencia.
El método (c15:RK1 )-(c15:RK3) es consistente si y sólo si ![]() .
.
Si el método es consistente, entonces el error de truncatura local es ![]() .
.
Valores moderados de ![]() conducen a algunos métodos
explícitos particulares.
conducen a algunos métodos
explícitos particulares.
![]()
Método de Euler modificado 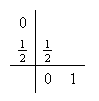
Método de Euler mejorado 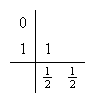
![]()
Método de Heun 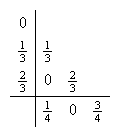
Método de Kutta 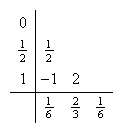
![]() Método clásico de Runge-Kutta
Método clásico de Runge-Kutta