A veces es necesario calcular el valor, ![]() , que el funcional
, que el funcional ![]() asigna a
la función
asigna a
la función ![]() perteneciente a un conjunto
perteneciente a un conjunto ![]() . Algunos ejemplos son los
siguientes:
. Algunos ejemplos son los
siguientes:
![]() , siendo
, siendo
![]() el
conjunto de las funciones derivables en
el
conjunto de las funciones derivables en ![]() .
.
![]() , siendo
ahora
, siendo
ahora ![]() el espacio de las funciones que admiten derivada tercera en
el espacio de las funciones que admiten derivada tercera en
![]() .
.
![]() , donde
, donde
![]() puede
ser el conjunto de las funciones integrables-Riemann en el intervalo
puede
ser el conjunto de las funciones integrables-Riemann en el intervalo ![]() .
.
En todos los casos, ![]() será un funcional lineal, es
decir,
será un funcional lineal, es
decir, ![]() para
cualesquiera elementos
para
cualesquiera elementos ![]() y
y ![]() del conjunto
del conjunto ![]() , y,
, y, ![]() , siendo
, siendo ![]() un escalar real
arbitrario y
un escalar real
arbitrario y ![]() perteneciente a
perteneciente a ![]() .
.
En muchas situaciones prácticas no será posible obtener explícitamente el
valor de ![]() . Por
ejemplo, si la variación de la concentración de un reactivo es proporcional a la
concentración existente en cada instante, resolviendo la ecuación diferencial
conocemos que la curva solución es de tipo exponencial. Pero, ?`cuánto vale la
pendiente en
. Por
ejemplo, si la variación de la concentración de un reactivo es proporcional a la
concentración existente en cada instante, resolviendo la ecuación diferencial
conocemos que la curva solución es de tipo exponencial. Pero, ?`cuánto vale la
pendiente en ![]() de la
curva que representa a la concentración si lo único que podemos medir es la
concentración en cada instante?, es decir, ?`cómo podemos calcular
de la
curva que representa a la concentración si lo único que podemos medir es la
concentración en cada instante?, es decir, ?`cómo podemos calcular ![]() ? No conocemos una expresión
explícita de la función
? No conocemos una expresión
explícita de la función ![]() Aunque el problema más
frecuente es que se necesite conocer el valor de una derivada primera o, a lo
sumo, la segunda, en un punto
Aunque el problema más
frecuente es que se necesite conocer el valor de una derivada primera o, a lo
sumo, la segunda, en un punto ![]() , también puede que se
necesite calcular una derivada de orden superior,
, también puede que se
necesite calcular una derivada de orden superior, ![]() , es decir que
, es decir que ![]() , y no se conoce una
expresión explícita de
, y no se conoce una
expresión explícita de ![]() (o, caso de conocerla, es
excesivamente compleja). Posiblemente sólo se conozca el valor de
(o, caso de conocerla, es
excesivamente compleja). Posiblemente sólo se conozca el valor de ![]() en puntos próximos al
en puntos próximos al ![]() , incluso en el propio
, incluso en el propio ![]() Ello servirá para aproximar
el valor de
Ello servirá para aproximar
el valor de ![]() . Es un
problema de derivación numérica.
. Es un
problema de derivación numérica.
Otro ejemplo. Sabemos que la función ![]() es continua en el intervalo
es continua en el intervalo
![]() .
Pero, ?`cómo podemos calcular
.
Pero, ?`cómo podemos calcular ![]() ? ?`Y
? ?`Y ![]() ? No existe una primitiva de
? No existe una primitiva de
![]() que se exprese en
términos elementales. En general, en muchas ocasiones hay que calcular el valor
que se exprese en
términos elementales. En general, en muchas ocasiones hay que calcular el valor
![]() para una función
para una función
![]() integrable en
integrable en ![]() ,
de la que no se conoce una primitiva y, por tanto, no podemos aplicar la regla
de Barrow. Posiblemente se conozca el valor que
,
de la que no se conoce una primitiva y, por tanto, no podemos aplicar la regla
de Barrow. Posiblemente se conozca el valor que ![]() toma en varios puntos del
intervalo
toma en varios puntos del
intervalo ![]() , a veces en todos los puntos del intervalo, incluso puede que
el valor de derivadas de
, a veces en todos los puntos del intervalo, incluso puede que
el valor de derivadas de ![]() en puntos del mismo. Esos
datos nos servirán para aproximar el valor de
en puntos del mismo. Esos
datos nos servirán para aproximar el valor de ![]() Es un problema de integración numérica.
Es un problema de integración numérica.
Podríamos dar más ejemplos, correspondientes a otros funcionales ![]() , pero son
los dos anteriores, derivación e integración, los más interesantes. En cualquier
caso, desde el punto de vista de la aproximación de
, pero son
los dos anteriores, derivación e integración, los más interesantes. En cualquier
caso, desde el punto de vista de la aproximación de ![]() mediante fórmulas de tipo interpolatorio, el tratamiento sería idéntico
en todos los casos: aproximar
mediante fórmulas de tipo interpolatorio, el tratamiento sería idéntico
en todos los casos: aproximar ![]() por un interpolante,
por un interpolante, ![]() , y tomar como aproximación
de
, y tomar como aproximación
de ![]() el valor
el valor ![]() Ni que decir tiene que el
espacio interpolador al que pertenece
Ni que decir tiene que el
espacio interpolador al que pertenece ![]() debe estar constituido por
funciones sencillas de forma que sea posible calcular
debe estar constituido por
funciones sencillas de forma que sea posible calcular ![]() .
.
Los polinomios son funciones muy sencillas de derivar y de integrar, por lo
que son muy utilizados como interpolantes para obtener fórmulas
de derivación e integración numéricas. Por ejemplo,
si se dispone de datos lagrangianos, podemos aproximar ![]() mediante el que
mediante el que ![]() asigna al
polinomio de interpolación de
asigna al
polinomio de interpolación de ![]() . Más concretamente, conocidos
los valores que
. Más concretamente, conocidos
los valores que ![]() toma en los nodos (distintos)
toma en los nodos (distintos)
![]() ,
, ![]() ,
, ![]() ,
, ![]() , sea
, sea ![]() el único polinomio tal que
el único polinomio tal que
![]() ,
, ![]() ;
entonces
;
entonces 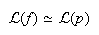 es una fórmula de tipo interpolatorio
para
es una fórmula de tipo interpolatorio
para ![]() en
en ![]() cuyos
nodos son
cuyos
nodos son ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Supongamos, por ejemplo, que ![]() es el polinomio de grado
menor o igual que uno que interpola a la función
es el polinomio de grado
menor o igual que uno que interpola a la función ![]() en los puntos
en los puntos ![]() y
y ![]() . Entonces
. Entonces
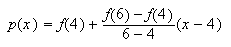 y, si
y, si ![]() , podemos
hacer
, podemos
hacer 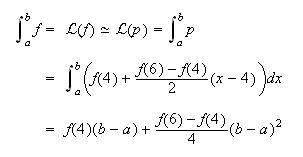
Tendríamos así una primera fórmula de integración numérica, de tipo
interpolatorio en ![]() , cuyos nodos son
, cuyos nodos son ![]() y
y ![]() (normalmente los
nodos pertenecen al intervalo
(normalmente los
nodos pertenecen al intervalo ![]() ).
).
Sin embargo, si ![]() , se tiene
, se tiene 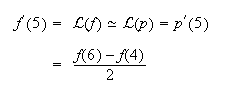 Es una
fórmula de derivación numérica, con dos nodos, que permite aproximar
Es una
fórmula de derivación numérica, con dos nodos, que permite aproximar ![]() a partir del valor de
a partir del valor de ![]() en los puntos
en los puntos ![]() y
y ![]() .
.
Tanto para las fórmulas de integración como las de derivación numérica, los
datos más habituales son los valores de la función en puntos distintos, llamados
nodos de la fórmula. El espacio interpolador suele ser el
de los polinomios de grado menor o igual que ![]() si hay
si hay ![]() datos. No obstante, podría
utilizarse otro espacio interpolador y los datos podrían ser distintos. Por
ejemplo, para aproximar la integral podrían usarse algunos datos derivada. En lo
que sigue, salvo que se especifique otra cosa, el espacio interpolador será
datos. No obstante, podría
utilizarse otro espacio interpolador y los datos podrían ser distintos. Por
ejemplo, para aproximar la integral podrían usarse algunos datos derivada. En lo
que sigue, salvo que se especifique otra cosa, el espacio interpolador será
![]() y los
datos serán lagrangianos, correspondientes a
y los
datos serán lagrangianos, correspondientes a ![]() nodos.
nodos.
El error de truncamiento, ![]() , cometido al aproximar
, cometido al aproximar ![]() mediante la fórmula de tipo
interpolatorio (c11:fti) es
mediante la fórmula de tipo
interpolatorio (c11:fti) es ![]() Como es conocido,
Como es conocido, ![]() es el error de
interpolación.
es el error de
interpolación.
En primer lugar, suponemos que es necesario aproximar la derivada primera de
![]() en un punto
en un punto ![]() , es decir
, es decir ![]() . Vamos a obtener fórmulas
con dos y tres nodos (con un solo nodo
. Vamos a obtener fórmulas
con dos y tres nodos (con un solo nodo ![]() se tiene
se tiene ![]() y, por tanto sería
y, por tanto sería ![]() , fórmula que carece de
interés por dar la misma aproximación para todas las funciones y para todo punto
, fórmula que carece de
interés por dar la misma aproximación para todas las funciones y para todo punto
![]() ).
).
Con dos nodos, ![]() y
y ![]() , se tiene que
, se tiene que
![]() y, por tanto, la
fórmula de derivación numérica es
y, por tanto, la
fórmula de derivación numérica es 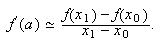
Es razonable que los nodos sean próximos a ![]() .. Si
.. Si ![]() y
y ![]() (con
(con ![]() ), la fórmula
es
), la fórmula
es 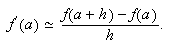 Si
Si ![]() tiende a cero, la
aproximación tiende al valor exacto cuando
tiende a cero, la
aproximación tiende al valor exacto cuando ![]() es derivable en
es derivable en ![]() ; por tanto, para
; por tanto, para ![]() muy pequeño, la
aproximación será buena cuando no se produzcan errores al evaluar
muy pequeño, la
aproximación será buena cuando no se produzcan errores al evaluar ![]() ni en las operaciones.
ni en las operaciones.
Si ![]() y
y
![]() , la fórmula
resultante es
, la fórmula
resultante es 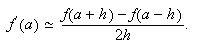
Con tres nodos, ![]() ,
, ![]() y
y ![]() , las siguientes
son las tres elecciones más importantes:
, las siguientes
son las tres elecciones más importantes:
![]() ,
, ![]() ,
, ![]() .
.
También da lugar a la fórmula (c11:fdn1).
![]() ,
,
![]() ,
, ![]() .
.
En este caso el polinomio de interpolación es 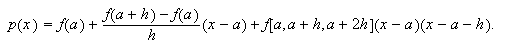 Es inmediato comprobar
que la fórmula de derivación numérica
Es inmediato comprobar
que la fórmula de derivación numérica ![]() se traduce en
se traduce en 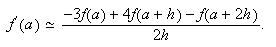
![]() ,
, ![]() ,
, ![]() .
.
Un proceso análogo da lugar a la fórmula 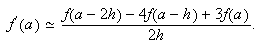
Del mismo modo podrían calcularse fórmulas con cuatro, cinco o más nodos.
A continuación vamos a ver fórmulas de tipo interpolatorio para la derivada
de orden ![]() , es
decir,
, es
decir, ![]() . Debe
haber tres o más nodos pues con dos el polinomio es de grado uno y su derivada
segunda es nula para toda función
. Debe
haber tres o más nodos pues con dos el polinomio es de grado uno y su derivada
segunda es nula para toda función ![]() y para todo punto
y para todo punto ![]() .
.
Con tres nodos, ![]() ,
, ![]() y
y ![]() , el polinomio
de interpolación
, el polinomio
de interpolación ![]() es
es 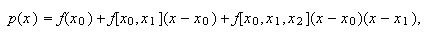 con lo
cual
con lo
cual ![]() .
Indicamos a continuación las tres elecciones más frecuentes.
.
Indicamos a continuación las tres elecciones más frecuentes.
![]() ,
, ![]() ,
, ![]() .
.
Da lugar a la fórmula 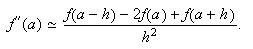
![]() ,
,
![]() ,
, ![]() .
.
Produce la fórmula 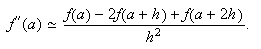
![]() ,
, ![]() ,
, ![]() .
.
En este caso, 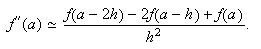
El proceso para las demás fórmulas de derivación numérica, tanto si es de
orden superior a dos (digamos ![]() ) como si los nodos son
diferentes de los considerados anteriormente, es totalmente análogo: se calcula
el polinomio de interpolación y se halla su derivada de orden
) como si los nodos son
diferentes de los considerados anteriormente, es totalmente análogo: se calcula
el polinomio de interpolación y se halla su derivada de orden ![]() en el punto
en el punto ![]() . Posteriormente daremos
otras fórmulas.
. Posteriormente daremos
otras fórmulas.
Teniendo en cuenta la expresión del error de interpolación en términos de
diferencias divididas, el error,![]() , de la fórmula de tipo
interpolatorio (c11:fti) se expresa como
, de la fórmula de tipo
interpolatorio (c11:fti) se expresa como 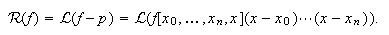 Por
tanto, teniendo en cuenta que las derivadas sucesivas de la diferencia dividida
Por
tanto, teniendo en cuenta que las derivadas sucesivas de la diferencia dividida
![]() son
son 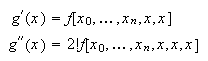 y, en
general,
y, en
general, 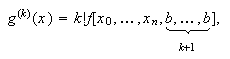 y que si
y que si ![]() , se verifica que
, se verifica que 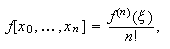 donde
donde
![]() , es fácil dar
expresiones del error de derivación numérica en función de cierta derivada de
, es fácil dar
expresiones del error de derivación numérica en función de cierta derivada de
![]() en un punto
en un punto ![]() . Sin embargo, en el caso de
las fórmulas de derivación numérica es fácil aprovechar el desarrollo de Taylor
de la función
. Sin embargo, en el caso de
las fórmulas de derivación numérica es fácil aprovechar el desarrollo de Taylor
de la función ![]() para
obtener una expresión del error. Por ejemplo, a partir de la fórmula
para
obtener una expresión del error. Por ejemplo, a partir de la fórmula 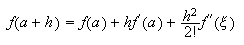 se
deduce que
se
deduce que 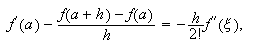 con lo cual tenemos el error para la
fórmula (c11:fdn0).
con lo cual tenemos el error para la
fórmula (c11:fdn0).
Análogamente, restando los desarrollos 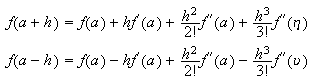 se tiene que
se tiene que  con
con
![]() , es decir, la
expresión del error asociado a la fórmula de derivación numérica (c11:fdn1).
, es decir, la
expresión del error asociado a la fórmula de derivación numérica (c11:fdn1).
De igual forma, se obtienen expresiones para las restantes fórmulas de
derivación numérica, aunque en algunos casos no es posible agrupar todos los
restos de Taylor en un solo sumando. No obstante, en todas las fórmulas de
derivación numérica, el error (de truncatura) es proporcional a una potencia de
![]() igual o superior a
igual o superior a
![]() . Así, cuando
. Así, cuando ![]() el
error de truncatura tiende a cero, pero al mismo tiempo estas fórmulas contienen
diferencias en el numerador de cantidades muy similares con lo que aparecen los
errores de cancelación, además del error de redondeo cometido al efectuar las
operaciones del numerador. El error total cometido al evaluar el numerador,
digamos de valor
el
error de truncatura tiende a cero, pero al mismo tiempo estas fórmulas contienen
diferencias en el numerador de cantidades muy similares con lo que aparecen los
errores de cancelación, además del error de redondeo cometido al efectuar las
operaciones del numerador. El error total cometido al evaluar el numerador,
digamos de valor ![]() , estará dividido por
, estará dividido por ![]() (o bien por
(o bien por ![]() , o por
, o por ![]() , etc.). Por
tanto, al ser
, etc.). Por
tanto, al ser ![]() pequeño,
el cociente adquiere un valor muy grande. En consecuencia, mientras que para la
truncatura es beneficioso disminuir
pequeño,
el cociente adquiere un valor muy grande. En consecuencia, mientras que para la
truncatura es beneficioso disminuir ![]() para el redondeo ocurre lo
contrario. El valor óptimo de
para el redondeo ocurre lo
contrario. El valor óptimo de ![]() es el que minimiza el error
total, es decir la suma del error de truncatura y el de redondeo (incluido en el
mismo el de cancelación). Así, para (c11:errorfdn1), si
es el que minimiza el error
total, es decir la suma del error de truncatura y el de redondeo (incluido en el
mismo el de cancelación). Así, para (c11:errorfdn1), si
![]() es una cota de la
derivada tercera de
es una cota de la
derivada tercera de ![]() , el error total
, el error total ![]() verifica que
verifica que 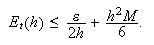
El mínimo del miembro de la derecha se alcanza cuando 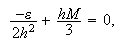 es
decir, para
es
decir, para 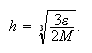 Por tanto, este valor de
Por tanto, este valor de ![]() será bueno para aplicar
dicha fórmula de derivación numérica, pero valores mucho menores que él pueden
conducir a estimaciones pésimas de la derivada.
será bueno para aplicar
dicha fórmula de derivación numérica, pero valores mucho menores que él pueden
conducir a estimaciones pésimas de la derivada.
A continuación recogemos varias fórmulas de derivación numérica para ![]() con
sus respectivos errores de truncatura (supuesto que se aplica a una función
suficientemente regular):
con
sus respectivos errores de truncatura (supuesto que se aplica a una función
suficientemente regular): 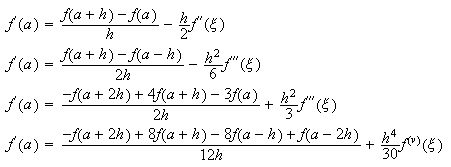 en lo que respecta la derivación de
segundo orden, disponemos de las siguientes:
en lo que respecta la derivación de
segundo orden, disponemos de las siguientes: 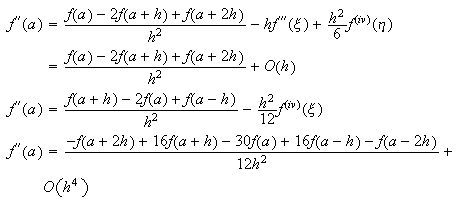
Supongamos ahora que el funcional lineal es ![]()
La fórmula de integración numérica basada en un nodo, ![]() , se obtiene
integrando el polinomio de interpolación
, se obtiene
integrando el polinomio de interpolación ![]() en el intervalo
en el intervalo ![]() :
:
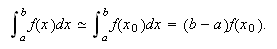
Gráficamente, si ![]() es no negativa, lo que se
hace es aproximar el área debajo de la curva
es no negativa, lo que se
hace es aproximar el área debajo de la curva ![]() , comprendida entre
, comprendida entre ![]() y
y ![]() por el área del
rectángulo de base
por el área del
rectángulo de base ![]() y altura
y altura ![]() (ver figura c11g1 ).
(ver figura c11g1 ).
Interpretación gráfica de la
fórmula del rectángulo.
Si ![]() , se
denomina fórmula del rectángulo izquierda ; si
, se
denomina fórmula del rectángulo izquierda ; si ![]() , fórmula del rectángulo derecha y fórmula del
punto medio si
, fórmula del rectángulo derecha y fórmula del
punto medio si ![]() . Son las siguientes,
respectivamente:
. Son las siguientes,
respectivamente: 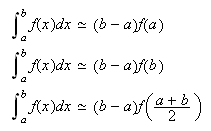
Con dos nodos, ![]() y
y ![]() , el polinomio
de interpolación es
, el polinomio
de interpolación es ![]() . La correspondiente
fórmula de integración numérica es
. La correspondiente
fórmula de integración numérica es 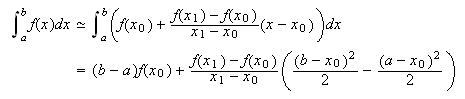
Si ![]() y
y
![]() , es la fórmula del trapecio (ver figura c11g2):
, es la fórmula del trapecio (ver figura c11g2):
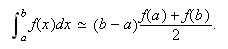
Interpretación geométrica de la
regla del trapecio.
Con tres nodos se tiene una de las fórmulas más importantes en la integración
numérica: la de Simpson. Corresponde a ![]() ,
, ![]() y
y
![]() (interpolación en
(interpolación en ![]() ). La fórmula de Lagrange
para el polinomio de interpolación es
). La fórmula de Lagrange
para el polinomio de interpolación es 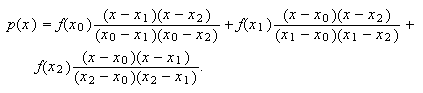 Sustituyendo los valores concretos
de los nodos e integrado entre
Sustituyendo los valores concretos
de los nodos e integrado entre ![]() y
y ![]() , se obtiene
, se obtiene 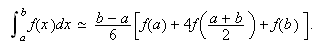 Obsérvese que el peso en el nodo central es cuatro veces
el peso en los extremos.
Obsérvese que el peso en el nodo central es cuatro veces
el peso en los extremos.
Para una fórmula de tipo interpolatorio el número de nodos de interpolación
puede ser mucho mayor que el usado antes. Además, los nodos pueden ser
diferentes; por ejemplo, nada nos impide para aproximar la integral entre ![]() usar los nodos
usar los nodos ![]() y
y ![]() en lugar de
los correspondientes a la fórmula del trapecio. Incluso, en lugar de interpolar
en
en lugar de
los correspondientes a la fórmula del trapecio. Incluso, en lugar de interpolar
en ![]() ,
podemos utilizar otro espacio de funciones (polinomios trigonométricos,
funciones spline, etc.). En definitiva, una infinidad de posibilidades
diferentes.
,
podemos utilizar otro espacio de funciones (polinomios trigonométricos,
funciones spline, etc.). En definitiva, una infinidad de posibilidades
diferentes.
Como ya dijimos, el error, ![]() , viene dado por la integral
del error de interpolación:
, viene dado por la integral
del error de interpolación: 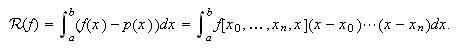 Deseamos encontrar una expresión en
la que aparezca el error en función de alguna derivada de
Deseamos encontrar una expresión en
la que aparezca el error en función de alguna derivada de ![]() .
.
El teorema del valor medio del cálculo integral permite extraer uno de los
factores del integrando siempre que sea continuo en ![]() y el que quede dentro sea integrable y no cambie de signo. En otros términos, si
y el que quede dentro sea integrable y no cambie de signo. En otros términos, si
![]() ,
, ![]() es integrable en
es integrable en ![]() y
y ![]() o
o ![]()
![]() , entonces existe
, entonces existe ![]() tal que
tal que ![]() .
.
En la expresión del error de integración numérica deseamos extraer del signo
integral la diferencia dividida ![]() . Para ello se necesita que
. Para ello se necesita que
![]() no cambie de
signo en
no cambie de
signo en ![]() . Ello ocurre, por ejemplo, para las fórmulas del rectángulo y
trapecio, pero no para las del punto medio y de Simpson. Veamos el error en
todas ellas.
. Ello ocurre, por ejemplo, para las fórmulas del rectángulo y
trapecio, pero no para las del punto medio y de Simpson. Veamos el error en
todas ellas.
Para la fórmula del rectángulo a la izquierda, el error es 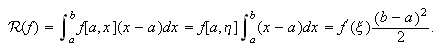 Análogamente, para la del rectángulo a la derecha,
Análogamente, para la del rectángulo a la derecha,
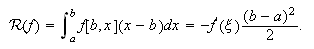
Para la fórmula del trapecio,
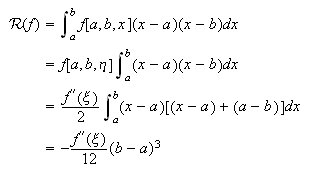
Para la del punto medio, 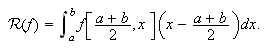 Ahora bien, la función
Ahora bien, la función ![]() cambia
de signo en
cambia
de signo en ![]() . No obstante, teniendo en cuenta la ley de recurrencia de las
diferencias divididas, como
. No obstante, teniendo en cuenta la ley de recurrencia de las
diferencias divididas, como 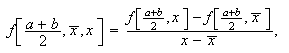 se deduce que
se deduce que 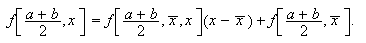
La última expresión es válida para todo ![]() Sustituyéndola en el
integrando de (c11:errorfin0) y dando a
Sustituyéndola en el
integrando de (c11:errorfin0) y dando a ![]() el valor
el valor
![]() , se tiene
que
, se tiene
que 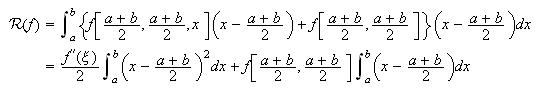 Como
Como ![]() ,
, 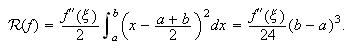
En lo que respecta al error de truncatura para la fórmula de Simpson, hay que
introducir un nodo auxiliar, ![]() , en la diferencia dividida
para conseguir un integrando que no cambie de signo. Operando como para la
fórmula del punto medio, obtenemos la expresión
, en la diferencia dividida
para conseguir un integrando que no cambie de signo. Operando como para la
fórmula del punto medio, obtenemos la expresión 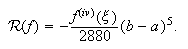
En todas las fórmulas anteriores el error es proporcional a una potencia de la longitud del intervalo de integración. Si el intervalo de integración es pequeño podemos esperar que el error sea pequeño, pero si es grande no tenemos esa garantía.
El intervalo de integración ![]() se puede dividir en
se puede dividir en ![]() subintervalos de igual
longitud,
subintervalos de igual
longitud, ![]() . Entonces, si elegimos como nodos los puntos
. Entonces, si elegimos como nodos los puntos ![]() ,
, ![]() , la
fórmula obtenida se denomina de Newton-Cotes abierta con
, la
fórmula obtenida se denomina de Newton-Cotes abierta con
![]() nodos. Por
ejemplo, con
nodos. Por
ejemplo, con ![]() se
obtiene la fórmula de Newton-Cotes con un solo nodo, que es la fórmula del punto
medio.
se
obtiene la fórmula de Newton-Cotes con un solo nodo, que es la fórmula del punto
medio.
Si elegimos como nodos los puntos ![]() ,
, ![]() , la
fórmula obtenida se denomina de Newton-Cotes cerrada con
, la
fórmula obtenida se denomina de Newton-Cotes cerrada con
![]() nodos. Por
ejemplo, con
nodos. Por
ejemplo, con ![]() se
obtiene la fórmula de Newton-Cotes con dos nodos, que es la fórmula del
trapecio. Con
se
obtiene la fórmula de Newton-Cotes con dos nodos, que es la fórmula del
trapecio. Con ![]() se
obtiene la de Simpson.
se
obtiene la de Simpson.
Otras fórmulas de Newton-Cotes, y sus errores de truncatura, son las siguientes:
fórmula 3/8 de Simpson
Con ![]() ,
, 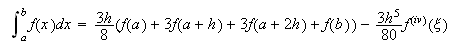
fórmula de Boole
Con ![]() ,
, 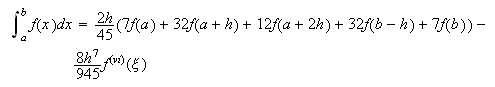
fórmula de Newton-Cotes abierta con dos nodos
Con ![]() ,
, 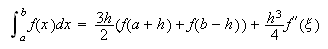
Podríamos dar muchas más fórmulas de Newton-Cotes, pero es conocido que la interpolación lagrangiana sobre puntos igualmente espaciados no es convergente (ejemplo de Runge). Luego no es recomendable usar una fórmula de Newton-Cotes con muchos nodos para obtener gran precisión.
Sin embargo, como la integral es aditiva, podemos descomponer el intervalo de
integración en ![]() subintervalos mediante una
partición uniforme del mismo con nodos
subintervalos mediante una
partición uniforme del mismo con nodos ![]() ,
, ![]() , y
expresar la integral en
, y
expresar la integral en ![]() como suma de integrales en
los intervalos inducidos por la partición:
como suma de integrales en
los intervalos inducidos por la partición: 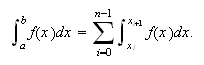
Si ![]() es grande
los intervalos de integración son pequeños con lo cual el error al aplicar una
fórmula de integración en cada uno puede que sea pequeño. El error total de
truncatura es la suma de los errores en cada subintervalo. Veremos
posteriormente que su valor tiende a cero cuando
es grande
los intervalos de integración son pequeños con lo cual el error al aplicar una
fórmula de integración en cada uno puede que sea pequeño. El error total de
truncatura es la suma de los errores en cada subintervalo. Veremos
posteriormente que su valor tiende a cero cuando ![]() .
.
Las fórmulas compuestas son las obtenidas al aplicar una misma fórmula simple
de integración numérica a cada uno de los sumandos de (c11:aditividad). Damos algunas a continuación (para
simplificar, notamos ![]() ,
, ![]() ).
).
Fórmula del rectángulo a la izquierda compuesta 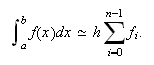
Fórmula del rectángulo derecho compuesta 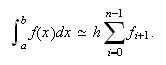
Fórmula del punto medio compuesta 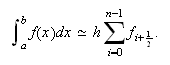
Fórmula del trapecio compuesta 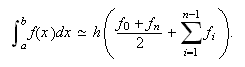
Fórmula de Simpson compuesta 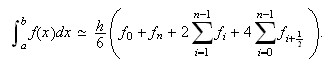
El error, ![]() , de una
fórmula compuesta es la suma de los errores,
, de una
fórmula compuesta es la suma de los errores, ![]() , cometidos en cada
subintervalo
, cometidos en cada
subintervalo ![]() al
aplicar la fórmula simple correspondiente. Por ejemplo, para la fórmula
compuesta resultante al aplicar la del rectángulo a la izquierda el error de
truncatura es
al
aplicar la fórmula simple correspondiente. Por ejemplo, para la fórmula
compuesta resultante al aplicar la del rectángulo a la izquierda el error de
truncatura es
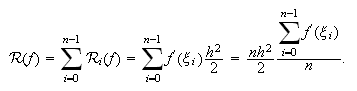 Ahora bien, la última fracción es la
media aritmética de los valores de la función
Ahora bien, la última fracción es la
media aritmética de los valores de la función ![]() en los
en los
![]() puntos
puntos ![]() . Como es un
valor comprendido entre el máximo y el mínimo de ellos, si
. Como es un
valor comprendido entre el máximo y el mínimo de ellos, si ![]() es
continua el teorema del valor intermedio garantiza la existencia de un punto
es
continua el teorema del valor intermedio garantiza la existencia de un punto
![]() , comprendido
entre los
, comprendido
entre los ![]() ,
tal que
,
tal que 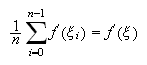 y, por tanto,
y, por tanto, 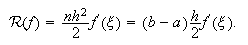 Si
Si
![]() está
acotada,
está
acotada, ![]() cuando
cuando
![]() .
.
Análogamente se obtiene el error para las demás fórmulas compuestas. La
expresión del error en la compuesta será similar al error de la fórmula simple
en un intervalo de longitud ![]() (con el valor
(con el valor ![]() perteneciente a todo el
intervalo
perteneciente a todo el
intervalo ![]() ) multiplicada por
) multiplicada por ![]() . A continuación recogemos
algunos de ellos.
. A continuación recogemos
algunos de ellos.
Fórmula del rectángulo a la derecha compuesta 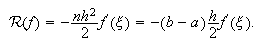
Fórmula del punto medio compuesta 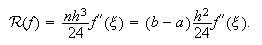
Fórmula del trapecio compuesta 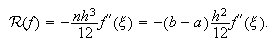
Fórmula de Simpson compuesta 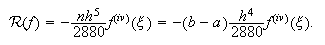
Por tanto, si ![]() es de la regularidad que
aparece en cada caso, la convergencia está asegurada ya que al tender
es de la regularidad que
aparece en cada caso, la convergencia está asegurada ya que al tender ![]() a cero (
a cero (![]() ) el error de truncatura
tiende a cero.
) el error de truncatura
tiende a cero.
Si ![]() es un
polinomo de grado menor o igual que
es un
polinomo de grado menor o igual que ![]() al ser interpolada por un
polinomio
al ser interpolada por un
polinomio ![]() de
de ![]() se
obtiene la misma función,
se
obtiene la misma función, ![]() , con lo cual el error de la
fórmula para dicha función es
, con lo cual el error de la
fórmula para dicha función es ![]() . Es decir, las fórmulas de
tipo interpolatorio son exactas para toda función de
. Es decir, las fórmulas de
tipo interpolatorio son exactas para toda función de ![]() .
Luego su orden de precisión es mayor o igual que
.
Luego su orden de precisión es mayor o igual que ![]() Para saber el orden exacto
sólo tendremos que calcular el error que se comete con las funciones
Para saber el orden exacto
sólo tendremos que calcular el error que se comete con las funciones ![]() (o bien con
las funciones
(o bien con
las funciones ![]() ), para
), para ![]() hasta que dicho error sea
distinto de cero. Por ejemplo, la fórmula del rectángulo (exacta en
hasta que dicho error sea
distinto de cero. Por ejemplo, la fórmula del rectángulo (exacta en ![]() )
da error diferente de cero para la función
)
da error diferente de cero para la función ![]() , ya que
, ya que ![]() Su orden de precisión es
cero. Sin embargo, para la fórmula del punto medio se cumple que
Su orden de precisión es
cero. Sin embargo, para la fórmula del punto medio se cumple que ![]() y
y ![]() , con la que la fórmula del
punto medio tiene orden de precisión
, con la que la fórmula del
punto medio tiene orden de precisión ![]() . Esto ya se sabía sin más
que observar la expresión del error. En la del rectángulo aparece la derivada
primera de la función mientras que en la del punto medio interviene la derivada
segunda. Es inmediato comprobar que la fórmula del trapecio tiene orden de
precisión
. Esto ya se sabía sin más
que observar la expresión del error. En la del rectángulo aparece la derivada
primera de la función mientras que en la del punto medio interviene la derivada
segunda. Es inmediato comprobar que la fórmula del trapecio tiene orden de
precisión ![]() y que la
de Simpson tiene orden de precisión 3. Análogamente, la
fórmula de derivación numérica
y que la
de Simpson tiene orden de precisión 3. Análogamente, la
fórmula de derivación numérica ![]() tiene orden de precisión
tiene orden de precisión
![]() , mientras que
, mientras que ![]() tiene orden de precisión
tiene orden de precisión
![]() . Es decir,
algunas elecciones de nodos son mejores que otras, puesto que con un solo nodo
tenemos unas fórmulas de integración numérica que tienen orden de precisión cero
y otra con precisión
. Es decir,
algunas elecciones de nodos son mejores que otras, puesto que con un solo nodo
tenemos unas fórmulas de integración numérica que tienen orden de precisión cero
y otra con precisión ![]() ; en derivación numérica,
con dos nodos hay fórmulas con precisión
; en derivación numérica,
con dos nodos hay fórmulas con precisión ![]() y otra con precisión
y otra con precisión![]() , etc.
, etc.
El orden de precisión es en todas ellas al menos ![]() pero ?`cuánto más puede
aumentar con una elección adecuada de los nodos? Suponiendo que los datos de
interpolación son todos lagrangianos, en las fórmulas para la derivada primera
no se puede aumentar el orden más allá del valor
pero ?`cuánto más puede
aumentar con una elección adecuada de los nodos? Suponiendo que los datos de
interpolación son todos lagrangianos, en las fórmulas para la derivada primera
no se puede aumentar el orden más allá del valor ![]() . Además, si
. Además, si ![]() , de (c11:errorfdn0) y (c11:errorfdn0a) se
deduce que
, de (c11:errorfdn0) y (c11:errorfdn0a) se
deduce que 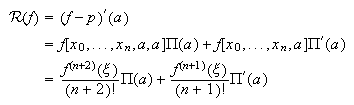 Se necesita que
Se necesita que ![]() para conseguir el orden
para conseguir el orden
![]() Para aumentar
más se necesitaría que
Para aumentar
más se necesitaría que ![]() por lo que
por lo que ![]() sería un cero doble de
sería un cero doble de
![]() y, por tanto,
tendríamos como dato el propio valor de
y, por tanto,
tendríamos como dato el propio valor de ![]() .
.
Veremos a continuación que, en lo que respecta a la integración numérica, es posible aumentar más la precisión.
Consideremos una fórmula de integración numérica de tipo interpolatorio con
![]() nodos,
nodos, 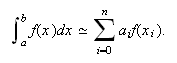
Demostración.- Si el oreden fuese igual o superior a
![]() no se cometería
error para la función
no se cometería
error para la función ![]() , es decir,
, es decir,
. 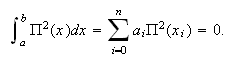 Pero dicha integral es mayor que
cero, puesto que
Pero dicha integral es mayor que
cero, puesto que ![]() y
y ![]() .
. ![]()
Demostración.- Condición necesaria. Si
el orden de precisión es ![]() , la fórmula es exacta para
las funciones
, la fórmula es exacta para
las funciones ![]() , para
, para
![]() , ya
que todas ellas pertenecen a
, ya
que todas ellas pertenecen a ![]() . En consecuencia,
. En consecuencia,  porque
porque
![]() para
para ![]() .
.
Condición suficiente. Sea ![]() . La
función
. La
función ![]() dividida por
dividida por ![]() da un
cociente
da un
cociente ![]() y un
resto
y un
resto ![]() , de
forma que
, de
forma que ![]() .
Entonces
.
Entonces 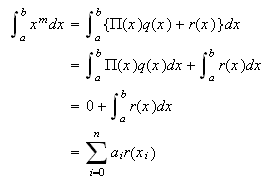 Pero
Pero ![]() , por lo que
, por lo que 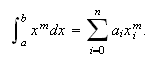
Es inmediato que la fórmula no es exacta para la función ![]() .
. ![]()
Por el teorema c11:gaussiana1 el valor máximo de ![]() es
es ![]() , para alcanzar la precisión
, para alcanzar la precisión
![]() , pero ?`será
posible? Se requiere, según el teorema c11:gaussiana2 que
, pero ?`será
posible? Se requiere, según el teorema c11:gaussiana2 que
![]() verifique las
igualdades
verifique las
igualdades 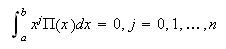 es decir, que
es decir, que ![]() sea el polinomio ortogonal
de grando
sea el polinomio ortogonal
de grando ![]() con
respecto al producto escalar
con
respecto al producto escalar ![]() , que existe y es único
salvo un factor multiplicativo. Además, sabemos que todas las raíces de dicho
polinomio son reales, simples e interiores al intervalo de integración. Así,
tenemos el siguiente resultado:
, que existe y es único
salvo un factor multiplicativo. Además, sabemos que todas las raíces de dicho
polinomio son reales, simples e interiores al intervalo de integración. Así,
tenemos el siguiente resultado:
Existen ![]() nodos
nodos ![]() , únicos,
todos interiores al intervalo
, únicos,
todos interiores al intervalo ![]() tales que la fórmula de
cuadratura de tipo interpolatorio correspondiente alcanza orden de precisión
tales que la fórmula de
cuadratura de tipo interpolatorio correspondiente alcanza orden de precisión
![]() .
.
A dicha fórmula se le denomina fórmula de Gauss con
![]() nodos. Para
construirla hemos de obtener primero el polinomio ortogonal de grado
nodos. Para
construirla hemos de obtener primero el polinomio ortogonal de grado ![]() , después calcular sus
raíces (que son los nodos de la fórmula) y finalmente obtener los coeficientes
de la fórmula.
, después calcular sus
raíces (que son los nodos de la fórmula) y finalmente obtener los coeficientes
de la fórmula.
La fórmula gaussiana más simple, con un solo nodo, es la del punto medio; su
orden de precisión es ![]() . Con dos nodos en el
intervalo
. Con dos nodos en el
intervalo ![]() el
polinomio ortogonal de grado
el
polinomio ortogonal de grado ![]() es
es ![]() ; sus
raíces son
; sus
raíces son ![]() y la fórmula gaussiana correspondiente es
y la fórmula gaussiana correspondiente es 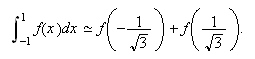 Para
la gaussiana con
Para
la gaussiana con ![]() nodos el polinomio
ortogonal es
nodos el polinomio
ortogonal es ![]() y sus raíces son
y sus raíces son ![]() y
y ![]() . Interpolando en esos
puntos e integrando se obtiene la fórmula
. Interpolando en esos
puntos e integrando se obtiene la fórmula 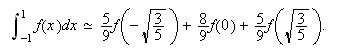
Si el intervalo es distinto del ![]() basta efectuar un cambio de
variable para obtener la fórmula correspondiente.
basta efectuar un cambio de
variable para obtener la fórmula correspondiente.
En lo que concierne al error relativo a las fórmulas gaussianas, realizando
el mismo procedimiento utilizado para calcular el error de la fórmula del punto
medio (escribir la diferencia dividida con un nodo más, aprovechando la ley de
recurrencia), solo que repitiéndolo tantas veces como nodos tiene la fórmula, se
llega a la siguiente expresión para la fórmula con ![]() nodos:
nodos: 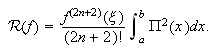
Si tuviésemos que aplicar una fórmula de integración numérica a un conjunto
de muchas funciones que tienen un factor común ![]() , siendo
, siendo ![]() mayor que cero salvo a lo
sumo en un conjunto finito de puntos (incluso en un conjunto infinito pero de
medida nula), sería interesante no tener que evaluar dicho factor en los nodos
de la fórmula sino repercutir su efecto en los coeficientes de la misma. Esto se
consigue mediante una fórmula del tipo
mayor que cero salvo a lo
sumo en un conjunto finito de puntos (incluso en un conjunto infinito pero de
medida nula), sería interesante no tener que evaluar dicho factor en los nodos
de la fórmula sino repercutir su efecto en los coeficientes de la misma. Esto se
consigue mediante una fórmula del tipo 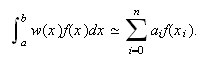 Suponemos que es posible calcular
las integrales
Suponemos que es posible calcular
las integrales ![]() .
.
Si se verifica que 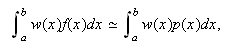 siendo
siendo ![]()
![]() ,
, ![]() , tenemos
una fórmula de integración numérica con función peso
, tenemos
una fórmula de integración numérica con función peso ![]() . Son fórmulas de tipo
interpolatorio y, por tanto, tienen orden de precisión mayor o igual que
. Son fórmulas de tipo
interpolatorio y, por tanto, tienen orden de precisión mayor o igual que ![]() . Eligiendo de nuevo los
nodos de forma adecuada puede conseguirse mayor orden. De hecho toda la teoría
correspondiente a las fórmulas gaussianas es idéntica, sólo que en los
integrandos aparece siempre el factor
. Eligiendo de nuevo los
nodos de forma adecuada puede conseguirse mayor orden. De hecho toda la teoría
correspondiente a las fórmulas gaussianas es idéntica, sólo que en los
integrandos aparece siempre el factor ![]() . Así, es posible alcanzar
la precisión
. Así, es posible alcanzar
la precisión ![]() eligiendo como nodos los ceros del polinomio ortogonal de grado
eligiendo como nodos los ceros del polinomio ortogonal de grado ![]() con respecto al producto
escalar
con respecto al producto
escalar 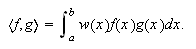
Dependiendo de ![]() y del intervalo
considerado, existen algunas fórmulas con función peso que tienen nombres
específicos. Concretamente si
y del intervalo
considerado, existen algunas fórmulas con función peso que tienen nombres
específicos. Concretamente si 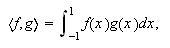 se denominan de Gauss-Legendre. Para
se denominan de Gauss-Legendre. Para 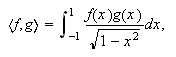 se denominan de Gauss-Chebyshev de primera especie. Si
se denominan de Gauss-Chebyshev de primera especie. Si 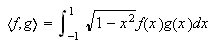 surgen
las de Gauss-Chebyshev de segunda especie. Cuando
surgen
las de Gauss-Chebyshev de segunda especie. Cuando 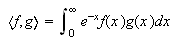 se
denominan de Gauss-Laguerre. Finalmente, si
se
denominan de Gauss-Laguerre. Finalmente, si 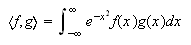 se
obtienen las fórmulas de Gauss-Hermite.
se
obtienen las fórmulas de Gauss-Hermite.
Un inconveniente de las fórmulas gaussianas es que sus nodos suelen ser
irracionales y en la práctica hay que aproximarlos por números racionales: las
fórmulas compuestas usan una partición unifiorme del intervalo de integración
(para aplicar la fórmula simple), sin tener en cuenta la la variación de la
función que se integra. Si embargo, es posible que ésta tenga comportamientos
muy diferentes a lo largo de dicho intervalo de integración, variando poco en
unas zonas y mucho en otras. Sería lógico considerar más puntos donde la
variación es mayor. Esa es la idea de la integración
adaptada a la variación de la función, que matizaremos después. Para cada
fórmula simple hay que encontrar el algoritmo que encuentra los nodos y aplica
dicha fórmula. El programa correspondiente que implementa ese algoritmo dentro
de un paquete de sofware se denomina Integrador Automático. En Mathematica se recoge bajo la orden
NIntegrate[f[x],{x,a,b}] (no conocemos a qué fórmula simple
corresponde, ni el algoritmo programado). Veamos el procedimiento que se debe
seguir para realizar una integración adaptada. Lo hacemos con la fórmula del
trapecio (se hace de forma análoga con las demás). Notamos por ![]() y por
y por ![]() los resultados de aplicar
la fórmula del trapecio simple y la del trapecio compuesta con dos subintervalos
(nodos
los resultados de aplicar
la fórmula del trapecio simple y la del trapecio compuesta con dos subintervalos
(nodos ![]() ,
, ![]() y
y ![]() ) a la integral de una
función
) a la integral de una
función ![]() . Teniendo
en cuenta las expresiones del error para las citadas fórmulas, podemos escribir
. Teniendo
en cuenta las expresiones del error para las citadas fórmulas, podemos escribir
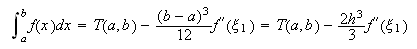 y
y
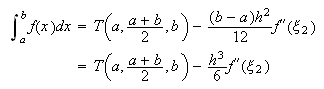 ya que
ya que ![]()
Ahora hacemos una hipótesis, a saber ![]() . De hecho, consideramos
que ambos valores son iguales y restamos las dos expresiones, obteniendo que
. De hecho, consideramos
que ambos valores son iguales y restamos las dos expresiones, obteniendo que
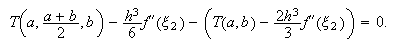 En consecuencia,
En consecuencia, 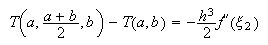 y
y 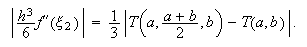
Si el valor del miembro de la derecha de la última expresión, que corresponde
al error de la fórmula del trapecio compuesta con ![]() subintervalos, es menor que
subintervalos, es menor que
![]() damos por
bueno
damos por
bueno ![]() como
aproximación de la integral. Pero como eso no ocurrirá normalmente, entonces se
divide el intervalo de integración en dos partes iguales y se aplica a cada una
el trapecio simple y el compuesto que resulta de subdividirlo de nuevo en dos
partes, permitiendo en cada una un error
como
aproximación de la integral. Pero como eso no ocurrirá normalmente, entonces se
divide el intervalo de integración en dos partes iguales y se aplica a cada una
el trapecio simple y el compuesto que resulta de subdividirlo de nuevo en dos
partes, permitiendo en cada una un error ![]() . Puede que uno de los
subintervalos cumpla la condición y el otro no. En tal caso, aquél en el que no
se cumple se divide en dos y se admite como error
. Puede que uno de los
subintervalos cumpla la condición y el otro no. En tal caso, aquél en el que no
se cumple se divide en dos y se admite como error ![]() en cada
uno; para el intervalo en el que se cumple se da por buena la aproximación
correspondiente a la fórmula del trapecio compuesta correspondiente. Hay que
continuar hasta que en todos los subintervalos que van apareciendo el error
quede acotado por la fracción de
en cada
uno; para el intervalo en el que se cumple se da por buena la aproximación
correspondiente a la fórmula del trapecio compuesta correspondiente. Hay que
continuar hasta que en todos los subintervalos que van apareciendo el error
quede acotado por la fracción de ![]() que le corresponda.
que le corresponda.
Resumiendo, en esta práctica se obtienen fórmulas de tipo interpolatorio, y se opera de dos formas:
Se obtiene el polinomio de interpolación, ![]() , de la función
, de la función ![]() a partir de las fórmulas
de Lagrange o Newton y se aproxima
a partir de las fórmulas
de Lagrange o Newton y se aproxima ![]() mediante
mediante ![]() .
.
Como la interpolación es exacta cuando ![]() es un polinomio de
es un polinomio de ![]() ,
la aproximación
,
la aproximación ![]() para
para ![]() se convierte en
se convierte en
![]() , resultado que
nos permite abordar la determinación de la fórmula para
, resultado que
nos permite abordar la determinación de la fórmula para ![]() imponiendo que
sea exacta en
imponiendo que
sea exacta en ![]() . Por ejemplo, la fórmula
de integración numérica del tipo
. Por ejemplo, la fórmula
de integración numérica del tipo 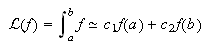 se calcula obligando a que sea
exacta en
se calcula obligando a que sea
exacta en ![]() , es decir, si
, es decir, si ![]() y
y ![]() , se impone que
se cumplan las condiciones
, se impone que
se cumplan las condiciones 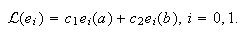
Si la fórmula de integración numérica es gaussiana, entonces debemos hallar el polinomio ortogonal adecuado, calcular sus raíces y utilizar éstas como nodos de interpolación.
Por último, debemos indicar que Mathematica dispone de órdenes específicas para manejar los polinomios ortogonales clásicos y de una orden especialmente diseñada para proporcionar una aproximación de la integral de una función con una alta exactitud, NIntegrate.