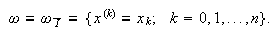 Si
dividimos
Si
dividimos Se puede dividir el intervalo cerrado ![]() en
en ![]() partes iguales, a partir de
una \underlinered uniforme con paso
partes iguales, a partir de
una \underlinered uniforme con paso ![]() y nodos
y nodos ![]()
![]()
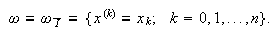 Si
dividimos
Si
dividimos ![]() en
en ![]() partes desiguales, entonces
tendremos una \underlinered no uniforme, con paso
variable
partes desiguales, entonces
tendremos una \underlinered no uniforme, con paso
variable ![]() .
.
Sobre estas redes consideraremos funciones discretas, que denominaremos
funciones de red, y que toman valores sobre los nodos de la red. Si tenemos
definida una función sobre el intervalo ![]() , podemos considerar dos
tipos de \underlinefunciones de red
, podemos considerar dos
tipos de \underlinefunciones de red
utilizando sólo información puntual, ![]() con
con![]()
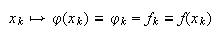
o bien, como una media de los valores de ![]() alrededor del
nodo, y utilizar así más información de la función
alrededor del
nodo, y utilizar así más información de la función ![]()
para los nodos interiores ![]() (también llamados
regulares, ver más adelante), se definiría
(también llamados
regulares, ver más adelante), se definiría ![]() como sigue
como sigue
![]()
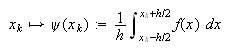
y para los nodos frontera, ![]()
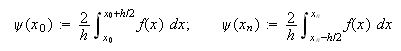
Si ahora tenemos un rectángulo ![]() considerando sendas redes
uniformes
considerando sendas redes
uniformes ![]() en
en ![]() ; podemos tomar el
producto cartesiano:
; podemos tomar el
producto cartesiano: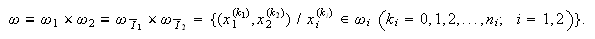 En cuanto a la notación, lo más
habitual en los casos de dimensión dos o tres es emplear las variables usuales:
con
En cuanto a la notación, lo más
habitual en los casos de dimensión dos o tres es emplear las variables usuales:
con ![]() (
(![]() y
y
![]() ) y
) y
![]() (
(![]()
![]() y
y
![]() ) por
ejemplo.
) por
ejemplo.
En general, si tomamos ![]()
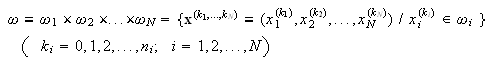 y diremos que la red
y diremos que la red ![]() es uniforme,
si lo son cada una de las
es uniforme,
si lo son cada una de las ![]()
Consideraremos aquí también funciones de red, que serán funciones discretas
que toman valores sobre los nodos de la red. Por ejemplo, si![]() está definida en el cierre
del dominio acotado
está definida en el cierre
del dominio acotado ![]() podemos definir las
siguientes funciones de red :
podemos definir las
siguientes funciones de red :
![]()
![]()
![]()
donde ![]() .
.
Distinguiremos a su vez dos tipos de puntos en ![]() , diremos que un nodo es
``\underlineregular'' o perteneciente a la ``parte
interior discretizada'' del dominio (que notaremos por
, diremos que un nodo es
``\underlineregular'' o perteneciente a la ``parte
interior discretizada'' del dominio (que notaremos por ![]() ) si todos los nodos
vecinos están también en
) si todos los nodos
vecinos están también en ![]() e ``\underlineirregular'' o perteneciente a la ``parte de la frontera
virtual discreta'' del dominio (simbolizada por
e ``\underlineirregular'' o perteneciente a la ``parte de la frontera
virtual discreta'' del dominio (simbolizada por ![]() ) en caso contrario. Más
adelante particularizaremos esto en el caso de dominios del plano curvilíneos
con una geometría arbitraria.
) en caso contrario. Más
adelante particularizaremos esto en el caso de dominios del plano curvilíneos
con una geometría arbitraria.
Si consideramos redes uniformes de paso![]() también podemos tomar para
cada nodo
también podemos tomar para
cada nodo ![]() una
función de red que tenga en cuenta los valores de la función
una
función de red que tenga en cuenta los valores de la función ![]() alrededor de dicho nodo,
mediante la correspondiente media (sólo para los nodos interiores regulares)
alrededor de dicho nodo,
mediante la correspondiente media (sólo para los nodos interiores regulares)
![]()
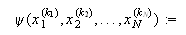
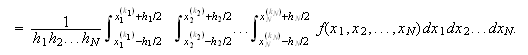
Dada una función ``de variable continua'' queremos definir funciones de red
para sus derivadas. En el caso de una variable sea ![]() y una red uniforme de paso
y una red uniforme de paso
![]() ,
, ![]() .
.
Para ![]() sea
sea
![]() el operador
derivada primera; los siguientes operadores discretos:
el operador
derivada primera; los siguientes operadores discretos: ![]()
![]() y
y![]() servirán para aproximar
servirán para aproximar
![]() (donde
(donde ![]() ,
,
![]() (diferencia izquierda)
(diferencia izquierda)
![]() (diferencia derecha)
(diferencia derecha)
![]() (diferencia central)
(diferencia central)
y notaremos ![]() si no hace falta referirse
al nodo.
si no hace falta referirse
al nodo.
Se comprueba que si ![]() efectivamente hay
convergencia de estos ope-ra-do-res discretos
efectivamente hay
convergencia de estos ope-ra-do-res discretos![]()
![]() en el sentido de que
en el sentido de que 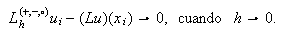 Basta
con desarrollar por Taylor:
Basta
con desarrollar por Taylor: 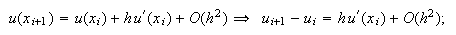
![]() luego
luego ![]()
\underlineEjercicio.- Hacer una demostración análoga
para ![]() y
y ![]() .
.
Para la derivada segunda, podemos considerar: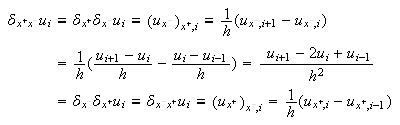
siendo ahora ![]()
\underlineEjercicio.- Obtener de forma análoga las
correspondientes aproximaciones ![]() y
y ![]() ; comprobar así mismo el
orden de aproximación de cada una de ellas.
; comprobar así mismo el
orden de aproximación de cada una de ellas.
Si consideramos ahora una función de dos variables ![]() definida en
definida en ![]() , entonces aproximamos
:
, entonces aproximamos
: (donde
(donde ![]() denota
denota ![]() ) y de igual modo
) y de igual modo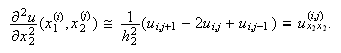
Por ejemplo, el operador Laplaciano se aproximará de la siguiente forma, si
tomamos incrementos iguales en ambas variables![]()
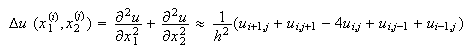
que se trata de una fórmula de 5 puntos en cruz. Y si tenemos que resolver la
ecuación de Laplace se tendría, igualando a cero la expresión anterior y
despejando: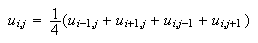
que sería una versión ``discreta'' del teorema de la media para funciones armónicas.
Por la fórmula de Taylor, se sigue que si ![]() entonces el error será de
orden 2, como se puede ver más en detalle:
entonces el error será de
orden 2, como se puede ver más en detalle: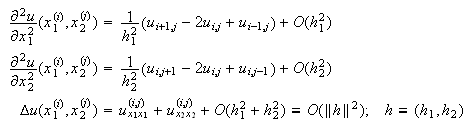
Tomaremos una red uniforme ![]() en
en ![]() de paso
de paso
![]() :
:
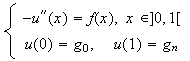
y definimos la siguiente ``función de red'': ![]()

Buscamos entonces otra función de red ![]() de manera que
de manera que
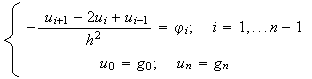
Obtenemos pues un sistema lineal de ![]() ecuaciones con
ecuaciones con ![]() incógnitas
incógnitas
![]() , de la forma
, de la forma
![]() donde:
donde:

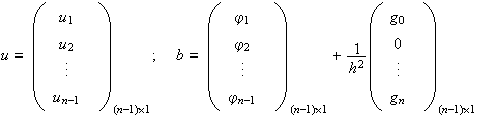
Se puede demostrar que este problema aproximado tiene solución única para
cada ![]() y
que si
y
que si ![]() la correspondiente solución
la correspondiente solución ![]() converje
hacia la solución exacta
converje
hacia la solución exacta ![]() en un sentido adecuado.
en un sentido adecuado.
Consideramos ahora un dominio rectangular ![]() , en el cual queremos
resolver de forma aproximada el siguiente problema de Dirichlet para la ecuación
de Poisson :
, en el cual queremos
resolver de forma aproximada el siguiente problema de Dirichlet para la ecuación
de Poisson :
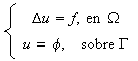
con funciones ![]() ;
; ![]() .
.
Para ello, utilizaremos una red ![]() producto de redes
producto de redes ![]() y
y![]() en
en
![]() e
e ![]() respectivamente.
respectivamente.
![]()
![]()
llamaremos ![]() al
conjunto de los nodos frontera, y aproximaremos
al
conjunto de los nodos frontera, y aproximaremos ![]() y
y ![]() por funciones de red
por funciones de red
![]()
![]() con
con ![]() o
o ![]()
Tendremos entonces el siguiente esquema en diferencias:
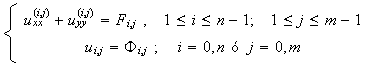
donde recordamos que
![]()
Y si por ejemplo tenemos ![]() entonces
entonces
![]()
Se puede probar que este método de diferencias finitas aplicado a la ecuación de Poisson con condiciones de Dirichlet, es un problema numérico bien planteado: es decir:
![]() , el
correspondiente sistema lineal tiene solución única, luego
, el
correspondiente sistema lineal tiene solución única, luego ![]() solución
aproximada para cada
solución
aproximada para cada ![]()
hay convergencia hacia la solución exacta en el siguiente sentido: si la
solución ![]() ,
entonces se cumple que:
,
entonces se cumple que:![]()

para cierta constante fija ![]() que no depende de
que no depende de ![]() de manera que si
de manera que si ![]() entonces el error
cometido tiende hacia
entonces el error
cometido tiende hacia ![]() y
y ![]() en el espacio
en el espacio ![]() .
.
Sea ![]() un
dominio (acotado) y consideramos planteado el siguiente problema de Dirichlet.
un
dominio (acotado) y consideramos planteado el siguiente problema de Dirichlet.
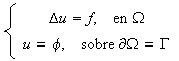
Si no conocemos detalladamente alguna de las características de la geometría
de ![]() que puede
tener una frontera curvilínea, procederemos mediante un método bastante general
y muy simple.
que puede
tener una frontera curvilínea, procederemos mediante un método bastante general
y muy simple.
Como ![]() está acotado, podremos encontrar intervalos
está acotado, podremos encontrar intervalos ![]() , de modo que
, de modo que ![]() (son acotados) y
(son acotados) y ![]()
Consideraremos purs ``redes'' uniformes ![]() en cada uno de estos
intervalos:
en cada uno de estos
intervalos:
![]()
![]()
y notaremos por ![]() la correspondiente red de
puntos de la malla
la correspondiente red de
puntos de la malla ![]() que están en
que están en ![]()
A su vez, distinguiremos dos tipos de puntos en ![]() , diremos que un nodo
, diremos que un nodo
![]() es
regular si los cuatro nodos vecinos están también en
es
regular si los cuatro nodos vecinos están también en ![]() e irregular en caso
contrario.
e irregular en caso
contrario.
Sea :
![]() es nodo regular
es nodo regular![]()
![]() es nodo irregular
es nodo irregular![]()
En el caso de la ecuación de Laplace (![]() ) y si los pasos en ambas
variables coinciden (
) y si los pasos en ambas
variables coinciden (![]() ) podremos entonces
aproximar la solución en
) podremos entonces
aproximar la solución en ![]() mediante un esquema
numérico de tipo cruz:
mediante un esquema
numérico de tipo cruz: 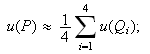 y para los puntos
situados en la frontera numérica del dominio
y para los puntos
situados en la frontera numérica del dominio ![]()
![]() siendo
siendo ![]() el pto. de
el pto. de ![]() "
más próximo" (en las direcciones de los ejes por ejemplo) a
"
más próximo" (en las direcciones de los ejes por ejemplo) a ![]() .
.
A la hora de resolver numéricamente problemas relacionados con las ecuaciones
del calor, de ondas o cualquier otro tipo de problema evolutivo (que dependa del
tiempo ![]() ), el
método de diferencias finitas visto anteriormente se aplica de forma inmediata
sin más que considerar las correspondientes aproximaciones de las derivadas
temporales, ya sean de primer o segundo orden.
), el
método de diferencias finitas visto anteriormente se aplica de forma inmediata
sin más que considerar las correspondientes aproximaciones de las derivadas
temporales, ya sean de primer o segundo orden.
En estos casos, si estamos especialmente interesados en la aproximación
numérica de la solución a lo largo del intervalo de tiempo ![]() , deberemos considerar la
correspondiente partición de este intervalo en el eje temporal, de la forma:
, deberemos considerar la
correspondiente partición de este intervalo en el eje temporal, de la forma:
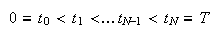 aunque la mayoría de las veces
conviene considerar estas particiones de manera que sean uniformes en
el siguiente sentido
aunque la mayoría de las veces
conviene considerar estas particiones de manera que sean uniformes en
el siguiente sentido
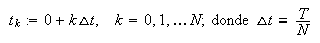 y se suele notar a las
aproximaciones
y se suele notar a las
aproximaciones ![]() .
.
Se dirá que estamos considerando un método \underline explícito si podemos ir despejando los valores de ![]() a
partir de los valores conocidos o calculados de la etapa anterior
a
partir de los valores conocidos o calculados de la etapa anterior ![]() e
\underlineimplícito en caso de que esto no pueda ser
así, y sea necesario resolver un sistema de ecuaciones en cada iteración de
tiempo, porque nuestro esquema involucre al mismo tiempo varias instancias de
e
\underlineimplícito en caso de que esto no pueda ser
así, y sea necesario resolver un sistema de ecuaciones en cada iteración de
tiempo, porque nuestro esquema involucre al mismo tiempo varias instancias de
![]() para
diferentes valores del índice
para
diferentes valores del índice ![]() al mismo tiempo.
al mismo tiempo.
Consideremos el siguiente problema mixto para la ecuación del calor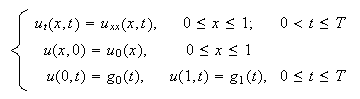 y
una red en
y
una red en ![]() con
pasos
con
pasos ![]() en tiempo y
en tiempo y ![]() en espacio; es decir
en espacio; es decir
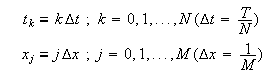
![]() representará el valor
exacto de la solución del problema en el nodo
representará el valor
exacto de la solución del problema en el nodo ![]() (suponemos
que dicha solución existe) y denotaremos por
(suponemos
que dicha solución existe) y denotaremos por ![]() a la función de red que
la aproxima.
a la función de red que
la aproxima.
En el instante ![]() podemos definir
podemos definir ![]() o si el dato
o si el dato ![]() no fuese muy
regular podría ser conveniente aproximar utilizando ciertos promedios:
no fuese muy
regular podría ser conveniente aproximar utilizando ciertos promedios:
![]()
Si suponemos ahora conocida la solución aproximada en el instante ![]() y vamos a
calcularla en
y vamos a
calcularla en ![]() utilizando datos de contorno:
utilizando datos de contorno: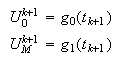 y para calcular
y para calcular ![]() discretizamos la ecuación
del calor del siguiente modo:
discretizamos la ecuación
del calor del siguiente modo:
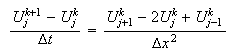 que despejando nos queda (con
que despejando nos queda (con
![]() ):
):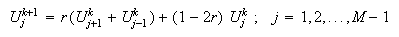 obteniéndose pues un método llamado \underlinede tipo
explícito, que requerirá la siguiente condición de estabilidad,
obteniéndose pues un método llamado \underlinede tipo
explícito, que requerirá la siguiente condición de estabilidad, ![]() para tener asegurada la convergencia
para tener asegurada la convergencia![]()
En el caso de los llamados \underlinemétodos de tipo
implícito, una vez inicializado el proceso: ![]() , pasamos de
, pasamos de ![]() a
a ![]() por medio
de las relaciones:
por medio
de las relaciones: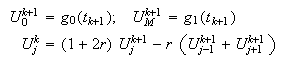
Se puede demostrar que si el problema tiene una solución suficientemente
regular, entonces y esto sin ningún tipo de
restricción respecto al paso de tiempo a tomar; es decir, el esquema resulta
\underline incondicionalmente convergente.
y esto sin ningún tipo de
restricción respecto al paso de tiempo a tomar; es decir, el esquema resulta
\underline incondicionalmente convergente.
Análogamente se pueden definir métodos numéricos, tanto de tipo explícito como implícito, para problemas de tipo hiperbólico (relacionados con la ecuación de ondas).