El Cálculo Numérico, o Análisis Numérico, como también se le denomina, es la
rama de las Matemáticas que estudia los métodos numéricos de resolución de
problemas, es decir, los métodos que permiten obtener una solución aproximada (a
veces exacta) del problema considerado tras realizar un número finito de
operaciones lógicas y algebraicas elementales. Los métodos numéricos son
imprescindibles para resolver aquellos problemas para los cuales no existen
métodos directos de resolución, o bien para aquellos otros en los que existe un
método directo pero no es viable, como ocurre con la regla de Cramer para la
resolución de sistemas lineales, que teóricamente es válida para resolver
cualquiera de ellos pero que en la práctica sólo es aplicable cuando la
dimensión es muy pequeña. El coste operacional de un
método es el número de operaciones que requiere su aplicación. Conocidos dicho
número y la velocidad de cálculo del ordenador, podemos saber el tiempo que
tardaría en ser resuelto. Por ejemplo, resolver un sistema lineal de orden poco
mayor que ![]() , con los
ordenadores actuales y aplicando la regla de Cramer, supondría más de un millón
de años, porque cuando el valor de un determinante de orden
, con los
ordenadores actuales y aplicando la regla de Cramer, supondría más de un millón
de años, porque cuando el valor de un determinante de orden ![]() se calcula como
se calcula como
![]() determinantes de
orden
determinantes de
orden ![]() el número
de operaciones que hay que hacer es, aproximadamente, del orden de
el número
de operaciones que hay que hacer es, aproximadamente, del orden de ![]() , valor que crece muy
rápidamente cuando
, valor que crece muy
rápidamente cuando ![]() aumenta.
aumenta.
Los métodos numéricos han sido utilizados desde la antigüedad en la búsqueda de soluciones aproximadas para los problemas procedentes de todas las ciencias y de las ingenierías. De hecho, hasta hace unos dos siglos la mayor parte de la matemática que se hacía era de tipo numérico y muchas de las demostraciones eran de tipo constructivo. No obstante, el nombre de Análisis Numérico aparece por primera vez en 1948, en California, donde se fundó el Instituto de Análisis Numérico, y su desarrollo ha sido paralelo al del ordenador, habiéndose producido un gran crecimiento en la segunda mitad del siglo XX, que continúa en la actualidad. Así pues, el Análisis Numérico tal y como se concibe hoy es una materia reciente. El ordenador es una herramienta imprescindible para esta disciplina, ya que los métodos numéricos requieren un gran número de cálculos y manipulaciones de datos.
Como hemos indicado, un método numérico es un procedimiento para aproximar la
solución de un problema. Un algoritmo es una descripción,
sin ambigüedad, de un proceso -o sucesión finita de pasos- que se puede seguir
para obtener la solución aproximada de dicho problema. Incluye desde la entrada
de datos hasta la impresión de resultados. Puede establecerse más de un
algoritmo para resolver un mismo problema. Un algoritmo se puede esquematizar
como sigue: 
Los dos ejemplos extremadamente simples que siguen ilustran este esquema.
Ejemplo 1. Algoritmo para hallar la suma, ![]() , de
, de ![]() números reales,
números reales, ![]()

Ejemplo 2. Algoritmo para calcular el producto, ![]() , de las componentes no
nulas de un vector
, de las componentes no
nulas de un vector ![]() de
de ![]()

Los ordenadores operan en un sistema que no suele ser el decimal (base ![]() ), sino que lo hacen en
binario (base
), sino que lo hacen en
binario (base ![]() ) o en otro
cuya base sea una potencia de
) o en otro
cuya base sea una potencia de ![]() (por ejemplo
(por ejemplo ![]() ). Sin embargo la
comunicación con el ordenador se hace siempre en base
). Sin embargo la
comunicación con el ordenador se hace siempre en base ![]() . Los datos numéricos que
damos al ordenador están escritos en el sistema decimal y los resultados
numéricos que el ordenador devuelve también. Para pasar un número de la base
decimal a la binaria debemos dividir entre
. Los datos numéricos que
damos al ordenador están escritos en el sistema decimal y los resultados
numéricos que el ordenador devuelve también. Para pasar un número de la base
decimal a la binaria debemos dividir entre ![]() y anotar el resto, volver a
dividir el cociente anterior entre
y anotar el resto, volver a
dividir el cociente anterior entre ![]() y anotar el resto, y así
sucesivamente hasta que el cociente sea cero. Los restos escritos en orden
inverso al que se han obtenido proporcionan la expresión del número en binario.
Por ejemplo, para escribir el número
y anotar el resto, y así
sucesivamente hasta que el cociente sea cero. Los restos escritos en orden
inverso al que se han obtenido proporcionan la expresión del número en binario.
Por ejemplo, para escribir el número ![]() del sistema decimal en el
sistema binario se realizan las operaciones que se indican a continuación:
del sistema decimal en el
sistema binario se realizan las operaciones que se indican a continuación:
| Resto | ||||
Los restos dan ![]() como expresión binaria de
como expresión binaria de
![]() , lo que podemos
notar como
, lo que podemos
notar como ![]() . El paso de la representación binario a decimal es muy fácil;
por ejemplo,
. El paso de la representación binario a decimal es muy fácil;
por ejemplo, 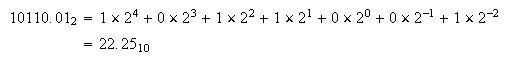
Números que tienen una representación finita en el sistema decimal pueden
tener una representación infinita en binario y viceversa. Por ejemplo, ![]() , donde la parte señalada se
repite periódicamente. Al introducir el número
, donde la parte señalada se
repite periódicamente. Al introducir el número ![]() en un ordenador que opere en
binario tiene que ser aproximado redondeándolo por defecto o por exceso a un
número cuya representación sea admisible por el ordenador (un número máquina, es decir, una cadena finita de ceros y unos).
en un ordenador que opere en
binario tiene que ser aproximado redondeándolo por defecto o por exceso a un
número cuya representación sea admisible por el ordenador (un número máquina, es decir, una cadena finita de ceros y unos).
La notación científica (o coma flotante) para representar los números en el
ordenador consta de signo, mantisa y
exponente; es decir, un número diferente de cero queda
representado de la forma 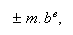 donde la mantisa
donde la mantisa ![]() es un número comprendido
entre
es un número comprendido
entre ![]() y
y ![]() cuyo primer dígito es no
nulo;
cuyo primer dígito es no
nulo; ![]() es la base
(
es la base
(![]() cuando estamos en
el sistema decimal), que no es necesario dar; y
cuando estamos en
el sistema decimal), que no es necesario dar; y ![]() es el exponente. Pensemos,
por ejemplo, en
es el exponente. Pensemos,
por ejemplo, en ![]() o
o ![]() . Para
representar en binario el signo, la mantisa y el exponente de un número se usa
una cadena de bit
. Para
representar en binario el signo, la mantisa y el exponente de un número se usa
una cadena de bit ![]() Un bit es un elemento físico
que admite dos estados que, por tanto, podemos hacer corresponder al
Un bit es un elemento físico
que admite dos estados que, por tanto, podemos hacer corresponder al ![]() y al
y al ![]() Una cadena de bit se puede
hacer corresponder a una de
Una cadena de bit se puede
hacer corresponder a una de ![]() y
y ![]() , y así obtener números en
binario. Con un bit también podemos representar los dos signos
, y así obtener números en
binario. Con un bit también podemos representar los dos signos ![]() y
y ![]() . Matemáticamente, la cadena
de bit que se usa para representar a un número equivale a una sucesión finita de
ceros y unos. El primero de ellos se emplea para representar el signo del
número, la mayor parte de los siguientes para la mantisa y los restantes para el
exponente. No es imprescindible reservar una posición para el signo del
exponente, ya que podemos realizar una traslación interna de los exponentes y,
así, representar exponentes tanto positivos como negativos de, aproximadamente,
igual valor. Por ejemplo, con siete cifras en binario se puede conseguir
representar los números del
. Matemáticamente, la cadena
de bit que se usa para representar a un número equivale a una sucesión finita de
ceros y unos. El primero de ellos se emplea para representar el signo del
número, la mayor parte de los siguientes para la mantisa y los restantes para el
exponente. No es imprescindible reservar una posición para el signo del
exponente, ya que podemos realizar una traslación interna de los exponentes y,
así, representar exponentes tanto positivos como negativos de, aproximadamente,
igual valor. Por ejemplo, con siete cifras en binario se puede conseguir
representar los números del ![]() al
al ![]() ; restando a todos ellos
; restando a todos ellos
![]() , tendríamos como
exponentes todos los números comprendidos entre
, tendríamos como
exponentes todos los números comprendidos entre ![]() y
y ![]() .
.
Una situación normal es disponer de ![]() bit, de los que uno se
dedica al signo,
bit, de los que uno se
dedica al signo, ![]() a la mantisa y
a la mantisa y ![]() al exponente. Los
exponenetes posibles irán desde el
al exponente. Los
exponenetes posibles irán desde el ![]() hasta el
hasta el ![]() , de tal forma que, si se
contempla un desplazamiento automático de
, de tal forma que, si se
contempla un desplazamiento automático de ![]() , tendríamos como posibles
exponentes los valores enteros comprendidos entre
, tendríamos como posibles
exponentes los valores enteros comprendidos entre ![]() y
y ![]() , y el rango de
números positivos con que podríamos trabajar va, aproximadamente, de
, y el rango de
números positivos con que podríamos trabajar va, aproximadamente, de ![]() hasta
hasta ![]() . La precisión es de
. La precisión es de ![]() , es decir, de unas
, es decir, de unas ![]() cifras decimales. Si tras
una operación se obtiene un valor superior a
cifras decimales. Si tras
una operación se obtiene un valor superior a ![]() se produce
un desbordamiento (overflow). Un valor inferior a
se produce
un desbordamiento (overflow). Un valor inferior a ![]() es tomado
como
es tomado
como ![]() (underflow)
(underflow)
Sólo un conjunto finito de números puede ser representado en el ordenador de
forma exacta. En nuestro ejemplo, el siguiente a ![]() es
es 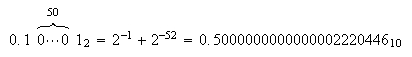 Cualquier otro número intermedio entre estos dos tiene que ser aproximado por
uno de ellos (redondeo). Si se aproxima por el más cercano se dice que el
redondeo es simétrico; si se cortan todos los dígitos de
la representación que sobrepasan la dimensión de la mantisa el redondeo es por
corte. Por ejemplo, en binario, con
Cualquier otro número intermedio entre estos dos tiene que ser aproximado por
uno de ellos (redondeo). Si se aproxima por el más cercano se dice que el
redondeo es simétrico; si se cortan todos los dígitos de
la representación que sobrepasan la dimensión de la mantisa el redondeo es por
corte. Por ejemplo, en binario, con ![]() dígitos, el redondeo
simétrico de
dígitos, el redondeo
simétrico de ![]() es
es
![]() ,
mientras que por corte es redondeado a
,
mientras que por corte es redondeado a ![]() .
.
A partir de ahora suponemos que todos los números están escritos en sistema decimal y no lo indicaremos.
El número máximo de decimales que soporta el ordenador en la representación
interna de un número real se denomina precisión. Supongamos
que la precisión es ![]() ; entonces todo número real
se puede representar de la forma
; entonces todo número real
se puede representar de la forma 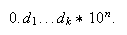 De hecho, supuesto que el redondeo
sea simétrico, ese mismo número máquina representa a todos los números del intervalo
De hecho, supuesto que el redondeo
sea simétrico, ese mismo número máquina representa a todos los números del intervalo
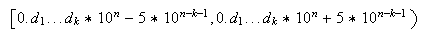 Por ejemplo, si la precisión es
Por ejemplo, si la precisión es ![]() , el número
, el número ![]() representa indistintamente
a todos los números del intervalo
representa indistintamente
a todos los números del intervalo 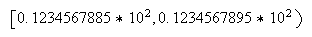 La diferencia entre cualquiera de estos
números y
La diferencia entre cualquiera de estos
números y ![]() es el error de redondeo
correspondiente. Lógicamente, los errores de redondeo se producen tanto en la
entrada y salida de los datos, como en todas las operaciones intermedias. Por
ejemplo, si la precisión del ordenador fuese de
es el error de redondeo
correspondiente. Lógicamente, los errores de redondeo se producen tanto en la
entrada y salida de los datos, como en todas las operaciones intermedias. Por
ejemplo, si la precisión del ordenador fuese de ![]() cifras y hubiese que multiplicar
los números
cifras y hubiese que multiplicar
los números ![]() y
y ![]() , entonces
el valor
, entonces
el valor ![]() tiene
que aproximarse por
tiene
que aproximarse por ![]() si redondea de forma simétrica
, o por
si redondea de forma simétrica
, o por ![]() si se redondea por corte.
si se redondea por corte.
Reorganizando la memoria del ordenador se puede aumentar la precisión en los redondeos. De hecho, desde los primeros ordenadores se pudo trabajar en doble precisión. Programas como Mathematica van mucho más allá y son capaces de aumentar la precisión sin más límite que la memoria del ordenador.
A continuación se comentan brevemente algunos conceptos básicos.
Si ![]() es la
solución exacta de un problema y
es la
solución exacta de un problema y ![]() es una aproximación de la
misma, entonces
es una aproximación de la
misma, entonces ![]() es el error
absoluto cometido. Si no tenemos más información, el error absoluto no
dice nada por sí solo; por ejemplo, el error absoluto en una pesada fue de
es el error
absoluto cometido. Si no tenemos más información, el error absoluto no
dice nada por sí solo; por ejemplo, el error absoluto en una pesada fue de ![]() gramos. Cuando
gramos. Cuando ![]() se denomina
error relativo a
se denomina
error relativo a ![]() . Como, en general, no se
conoce
. Como, en general, no se
conoce ![]() , el error
relativo se suele aproximar por el valor
, el error
relativo se suele aproximar por el valor ![]() . El error relativo tiene
que ser muy próximo a cero para que la aproximación sea buena; por ejemplo, si
el peso exacto debía ser
. El error relativo tiene
que ser muy próximo a cero para que la aproximación sea buena; por ejemplo, si
el peso exacto debía ser ![]() gramos, se habría cometido
un error muy importante y el error relativo sería
gramos, se habría cometido
un error muy importante y el error relativo sería ![]() . Sin embargo, el error
relativo sería
. Sin embargo, el error
relativo sería ![]() y el error absoluto
despreciable si el peso exacto fuese
y el error absoluto
despreciable si el peso exacto fuese ![]() Kg.
Kg.
En la práctica no se suelen conocer los errores absoluto y relativo, sino
cotas de los mismos, ![]() y
y ![]() , de
tal forma que se verifican las desigualdades
, de
tal forma que se verifican las desigualdades ![]() y
y ![]()
![]() .
También se suele notar
.
También se suele notar ![]() y
y ![]() , o a la inversa
, o a la inversa ![]() y
y ![]() .
.
Supuesto que se conozcan cotas para los errores absoluto y relativo de unas
cantidades ![]() ,
, ![]() ,
, ![]() es
interesante conocer una cota del resultado obtenido al efectuar una operación
elemental (
es
interesante conocer una cota del resultado obtenido al efectuar una operación
elemental (![]() )
con las mismas. Es inmediato comprobar que
)
con las mismas. Es inmediato comprobar que 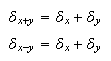 ya que, si
ya que, si ![]() e
e ![]() , entonces
, entonces
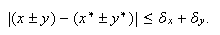
En cuanto al error relativo en la suma o la resta, de ![]() e
e ![]() se deduce que
se deduce que ![]() ; por tanto, supuesto que
; por tanto, supuesto que
![]() , la
división por
, la
división por ![]() conduce
a la igualdad
conduce
a la igualdad 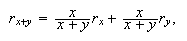 de tal forma que, si tanto
de tal forma que, si tanto ![]() como
como ![]() son de igual signo, se tiene
son de igual signo, se tiene
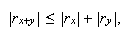 es decir,
es decir, 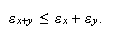 Pero si
Pero si ![]() e
e ![]() tienen signos opuestos y
valores muy similares el error relativo se puede disparar.
Es el efecto de la cancelación que se produce al restar cantidades casi iguales
que comentaremos después.
tienen signos opuestos y
valores muy similares el error relativo se puede disparar.
Es el efecto de la cancelación que se produce al restar cantidades casi iguales
que comentaremos después.
En cuanto al producto y al cociente, supondremos que el producto de ![]() por
por ![]() y los cuadrados de ellos
son cantidades despreciables.
y los cuadrados de ellos
son cantidades despreciables.
Para la multiplicación se tiene que 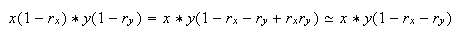 por tanto, el error relativo en la
multiplicación está acotado (aproximadamente) por
por tanto, el error relativo en la
multiplicación está acotado (aproximadamente) por 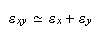
De forma análoga, para el cociente se llega a la misma cota: 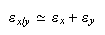
En lo que se refiere a la evaluación en un punto ![]() de la función
de la función ![]() , que suponemos derivable
con continuidad, del desarrollo de Taylor se deduce que
, que suponemos derivable
con continuidad, del desarrollo de Taylor se deduce que 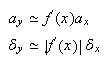 De
forma análoga, si
De
forma análoga, si ![]() es una función de varias
variables,
es una función de varias
variables,![]() ,
digamos
,
digamos ![]() , una
cota del error absoluto es
, una
cota del error absoluto es 
Un desarrollo teórico más extenso sobre propagación de los errores en los operaciones escapa del interés de este libro. Una introducción suele encontrarse en muchos libros de Análisis Numérico; en general, una acotación del error cometido después de miles o millones de operaciones suele ser un valor muy pesimista, ya que supondría que el error es siempre de igual signo y se acumula, hecho que en la práctica rara vez ocurre.
Si ![]() es el
mayor entero para el cual
es el
mayor entero para el cual 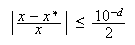 se dice que
se dice que ![]() aproxima
a
aproxima
a ![]() con
con ![]() dígitos
decimales significativos. Por ejemplo, para
dígitos
decimales significativos. Por ejemplo, para ![]() se tiene que
se tiene que ![]() es
una aproximación con cuatro dígitos significativos ya que
es
una aproximación con cuatro dígitos significativos ya que 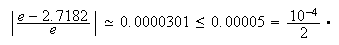
Cuando en un problema se dispone de una sucesión de valores, ![]() , convergente a la solución
del mismo y se usa un método numérico que emplee un valor
, convergente a la solución
del mismo y se usa un método numérico que emplee un valor ![]() como aproximación de la
solución, el error cometido se llama error de truncamiento
o truncatura. Por ejemplo, si consideramos la aproximación
como aproximación de la
solución, el error cometido se llama error de truncamiento
o truncatura. Por ejemplo, si consideramos la aproximación
![]() , cometemos el
error de truncadura
, cometemos el
error de truncadura ![]() Análogamente, a veces se
tiene fórmulas procedentes de despreciar el último término de un desarrollo
finito de Taylor. El error cometido es por truncamiento. Por ejemplo, como
Análogamente, a veces se
tiene fórmulas procedentes de despreciar el último término de un desarrollo
finito de Taylor. El error cometido es por truncamiento. Por ejemplo, como ![]() , entonces al aproximar la
derivada de
, entonces al aproximar la
derivada de ![]() en
en ![]() por
por 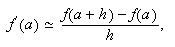 supuesto que no se cometan errores al evaluar la función
supuesto que no se cometan errores al evaluar la función ![]() en
en ![]() y en
y en ![]() , ni en la resta, ni en la
división, el error cometido es
, ni en la resta, ni en la
división, el error cometido es 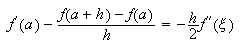 y corresponde al truncamiento
efectuado al despreciar el último término del desarrollo de Taylor.
y corresponde al truncamiento
efectuado al despreciar el último término del desarrollo de Taylor.
Pero el ejemplo anterior, correspondiente a la aproximación de la derivada,
es apropiado para mostrar la aparición de otros errores. Cuando ![]() es pequeño las cantidades
es pequeño las cantidades
![]() y
y ![]() son muy similares, cada vez tendrán mayor número de cifras coincidentes y, por
tanto, al efectuar la resta se pierden cifras significativas. Es lo que se
denomina error por cancelación. Siempre que se restan
cantidades muy próximas se produce un error por cancelación, que puede pasar a a
ser un error muy grande cuando va multiplicado por un valor grande, como en el
ejemplo anterior, en el que el factor
son muy similares, cada vez tendrán mayor número de cifras coincidentes y, por
tanto, al efectuar la resta se pierden cifras significativas. Es lo que se
denomina error por cancelación. Siempre que se restan
cantidades muy próximas se produce un error por cancelación, que puede pasar a a
ser un error muy grande cuando va multiplicado por un valor grande, como en el
ejemplo anterior, en el que el factor ![]() puede ser grande. Aparecen
en la fórmula de derivación numérica dos errores con comportamiento diferente
respecto del valor de
puede ser grande. Aparecen
en la fórmula de derivación numérica dos errores con comportamiento diferente
respecto del valor de ![]() : el de truncamiento, que
decrece cuando
: el de truncamiento, que
decrece cuando ![]() disminuye (prácticamente
proporcional a
disminuye (prácticamente
proporcional a ![]() ), y el de cancelación y
redondeo en el numerador (digamos
), y el de cancelación y
redondeo en el numerador (digamos ![]() ) que va dividido por
) que va dividido por ![]() , es decir, inversamente
proporcional a
, es decir, inversamente
proporcional a ![]() . No por disminuir
. No por disminuir ![]() más y más el error va a ser
menor. Al contrario, llegará un momento en el que aumentará rápidamente debido
al término
más y más el error va a ser
menor. Al contrario, llegará un momento en el que aumentará rápidamente debido
al término ![]() . Pero
llega otro momento en el que los valores de
. Pero
llega otro momento en el que los valores de ![]() y
y ![]() son idénticos para el ordenador, de tal forma que, aunque disminuya
son idénticos para el ordenador, de tal forma que, aunque disminuya ![]() , la aproximación de la
derivada será siempre
, la aproximación de la
derivada será siempre ![]() y el error será
y el error será ![]() .
.
Para algunos problemas podemos organizar los cálculos de forma que se evite
el error por cancelación. Por ejemplo, para todo ![]() , la
expresión
, la
expresión ![]() es
equivalente a
es
equivalente a ![]() , cuyo valor es próximo a
, cuyo valor es próximo a
![]() ;
sin embargo, para
;
sin embargo, para ![]() suficientemente grande la
primera expresión da cero (operando en modo científico).
suficientemente grande la
primera expresión da cero (operando en modo científico).
Muchas veces disponemos de una expresión que nos da, para cualquier ![]() , un valor
, un valor ![]() como aproximación del valor exacto
como aproximación del valor exacto ![]() y se sabe que existe una
constante
y se sabe que existe una
constante ![]() tal
que
tal
que 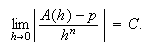 Entonces se dice que el error
absoluto
Entonces se dice que el error
absoluto ![]() es un
infinitésimo de orden
es un
infinitésimo de orden ![]() , y se expresa
, y se expresa ![]() . Para valores positivos y
pequeños de
. Para valores positivos y
pequeños de ![]() podemos
considerar
podemos
considerar 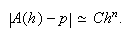
En ocasiones la expresión ![]() es una combinación de datos
relativos a una función
es una combinación de datos
relativos a una función ![]() (por ejemplo, una
combinación de valores de
(por ejemplo, una
combinación de valores de ![]() y de algunas de sus
derivadas), mientras que el valor
y de algunas de sus
derivadas), mientras que el valor ![]() correponde a una
manipulación de
correponde a una
manipulación de ![]() que sólo puede realizarse de
forma exacta para ciertas funciones (al menos las de tipo polinómico). En tal
caso, los polinomios constituyen unas funciones test para medir la bondad de la
aproximación, y se dice que
que sólo puede realizarse de
forma exacta para ciertas funciones (al menos las de tipo polinómico). En tal
caso, los polinomios constituyen unas funciones test para medir la bondad de la
aproximación, y se dice que ![]() tiene orden de precisión
tiene orden de precisión
![]() si es exacta para
las funciones
si es exacta para
las funciones ![]() ,
, ![]() ,
, ![]() ,
, ![]() y comete error distinto de
cero para la función
y comete error distinto de
cero para la función ![]() Por ejemplo, si usamos
Por ejemplo, si usamos
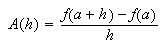 para aproximar el valor
para aproximar el valor ![]() , cuando
, cuando ![]() se obtiene
se obtiene ![]() y para
y para ![]() resulta que
resulta que ![]() , mientras que si
, mientras que si ![]() , se verifica que
, se verifica que 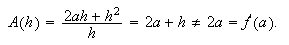 Por
tanto el orden de exactitud es
Por
tanto el orden de exactitud es ![]() .
.
Podemos identificar un problema como una entrada de datos, ![]() , que tras sufrir un
proceso,
, que tras sufrir un
proceso, ![]() , da una
salida
, da una
salida ![]() , lo que se
nota
, lo que se
nota ![]() . La
entrada
. La
entrada ![]() puede ser
un número, un vector, una matriz, etc. Lo mismo es válido para
puede ser
un número, un vector, una matriz, etc. Lo mismo es válido para ![]() . ?`Cómo se mide la
sensibilidad de
. ?`Cómo se mide la
sensibilidad de ![]() frente a pequeñas
variaciones de
frente a pequeñas
variaciones de ![]() , supuesto que el proceso
, supuesto que el proceso
![]() se realiza con
precisión infinita? En el caso más habitual en el que tanto
se realiza con
precisión infinita? En el caso más habitual en el que tanto ![]() como
como ![]() son distintos de cero, las
variaciones se consideran en términos relativos. El factor que las relaciona es
el condicionamiento. Veamos algún ejemplo.
son distintos de cero, las
variaciones se consideran en términos relativos. El factor que las relaciona es
el condicionamiento. Veamos algún ejemplo.
Supongamos que el proceso consiste en evaluar una función real, ![]() , en un punto,
, en un punto, ![]() , de modo que
, de modo que ![]() . Si
. Si ![]() es derivable, entonces
es derivable, entonces 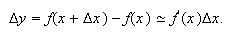 Como
suponemos que
Como
suponemos que ![]() , podemos escribir
, podemos escribir 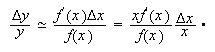 Esto sugiere definir el
condicionamiento de
Esto sugiere definir el
condicionamiento de ![]() en
en ![]() ,
, ![]() , por
, por  Mide
la perturbación relativa de
Mide
la perturbación relativa de ![]() frente a una perturbación
relativa de
frente a una perturbación
relativa de ![]() .
.
Cuando ![]() es una
función de
es una
función de ![]() en
en ![]() el condicionamiento de cada
una de las componentes
el condicionamiento de cada
una de las componentes ![]() respecto de cada una de las
variables
respecto de cada una de las
variables ![]() ,
,
![]() , es
, es 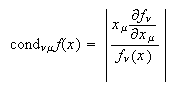
Para analizar la sensibilidad de ![]() frente a una perturbación
del vector
frente a una perturbación
del vector ![]() hemos de
considerar normas vectoriales y matriciales compatibles. Por ejemplo, si
hemos de
considerar normas vectoriales y matriciales compatibles. Por ejemplo, si ![]() representa la matriz
jacobiana de
representa la matriz
jacobiana de ![]() , empleando
la norma del máximo concluimos que
, empleando
la norma del máximo concluimos que 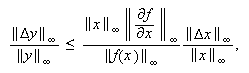 de forma que
de forma que 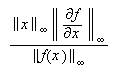 es el
condicionamiento en este caso.
es el
condicionamiento en este caso.
Uno de los problemas en los que con más frecuencia hay que estimar el
condicionamiento es el correspondiente a la resolución de sistemas lineales.
Como se verá en aquel tema, el condicionamiento de una matriz viene dado por el
producto de la norma de la matriz por la norma de su inversa, esto es ![]() . Un sistema puede ser de
dimensión muy pequeña y tener un mal condicionamiento. Por ejemplo, consideremos
la matriz
. Un sistema puede ser de
dimensión muy pequeña y tener un mal condicionamiento. Por ejemplo, consideremos
la matriz 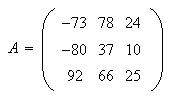 Su determinante vale
Su determinante vale ![]() . Su inversa es
. Su inversa es  Así,
con cualquier norma matricial
Así,
con cualquier norma matricial ![]() será grande y
será grande y ![]() muy grande. Concretamente,
si sumamos los valores absolutos de los elementos de cada fila y nos quedamos
con el mayor valor de los obtenidos (norma del máximo para matrices), se tiene
muy grande. Concretamente,
si sumamos los valores absolutos de los elementos de cada fila y nos quedamos
con el mayor valor de los obtenidos (norma del máximo para matrices), se tiene
![]() y
y ![]() con lo cual
con lo cual ![]() (un valor enorme). Los
condicionamientos bajos al trabajar con matrices son los que valen poco más de
la unidad.
(un valor enorme). Los
condicionamientos bajos al trabajar con matrices son los que valen poco más de
la unidad.
En todos los casos, si el condicionamiento (o número de condición) es alto se dice que el problema es mal condicionado y debemos cuidar mucho la precisión de los datos porque un pequeño error inicial en los mismos (por ejemplo, un redondeo) puede dar lugar a grandes diferencias en los resultados.
La estabilidad se refiere a la forma en que repercuten los errores iniciales
y los ocurridos durante el proceso en los resultados finales. Así, cuando estos
errores se van propagando y ampliando de forma muy considerable se dice que el
proceso es inestable, mientras que cuando los posibles errores iniciales y los
que surgen en el proceso van amortiguándose se dice que el proceso es estable.
El proceso de resolución de un problema puede ser bien condicionado y ser
inestable. La inestabilidad afecta a todo el proceso; por tanto, es posible que
cambiando el algoritmo de resolución pueda evitarse. Por ejemplo, es fácil
demostrar por inducción que la sucesión de valores ![]() puede generarse
indistintamente a partir de los siguientes algoritmos:
puede generarse
indistintamente a partir de los siguientes algoritmos:
![]() ,
,
![]()
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
, ![]() .
.
Sin embargo, con el segundo (operando con 6 cifras de precisión) el
decimosexto término es ![]() , frente al valor
, frente al valor ![]() .
.
Análogamente, la sucesión ![]() puede generarse a partir
del algoritmo
puede generarse a partir
del algoritmo ![]() ,
,
![]() ,
, ![]() ,
, ![]() , que
también es inestable.
, que
también es inestable.
Combinando estabilidad y condicionamiento sólo estamos seguros de que los resultados son correctos cuando aplicamos un algoritmo estable a un problema bien condicionado. En cualquiera de los otros tres casos no estamos seguros de que los resultados sean fiables.
Muchas veces no sabemos si el problema que estamos resolviendo está bien o
mal condicionado y si el algoritmo usado es estable o no. Lo único que sabemos
es que a partir de unos datos produce unos resultados. Si los resultados fuesen
precisos seguramente el problema estaría bien condicionado y el método de
resolución sería estable. Uno de los procedimientos más simples para estimar la
veracidad de los resultados es el método de
permutación-perturbación, que consiste en resolver el mismo problema
varias veces, permutando las operaciones (o parte del proceso) que sea posible y
redondeando los datos iniciales y los resultados intermedios cada vez, por
exceso o por defecto, de forma aleatoria. Entonces la media de los resultados,
![]() , dividida por la
desviación típica de los mismos,
, dividida por la
desviación típica de los mismos, ![]() , sirve como estimador
estadístico, de forma que
, sirve como estimador
estadístico, de forma que ![]() tiene que tener valores muy
similares (que disten menos de
tiene que tener valores muy
similares (que disten menos de ![]() ) cuando se aplica a dos
tandas de perturbaciones. En la práctica, si después de efectuar tres o cuatro
permutaciones-perturbaciones los resultados difieren poco en términos relativos
es casi seguro que son fiables.
) cuando se aplica a dos
tandas de perturbaciones. En la práctica, si después de efectuar tres o cuatro
permutaciones-perturbaciones los resultados difieren poco en términos relativos
es casi seguro que son fiables.
A veces el condicionamiento es tan malo que no es necesario recurrir a este estimador, sino que al aplicar varias perturbaciones los resultados son tan dispares que resulta evidente.
Por ejemplo, hemos aplicado a cada elemento de la matriz anterior, ![]() , una perturbación aleatoria
comprendida entre
, una perturbación aleatoria
comprendida entre ![]() y
y ![]() (sumando a cada
elemento de
(sumando a cada
elemento de ![]() el valor
-0.05 Random[]) y hemos resuelto el sistema
el valor
-0.05 Random[]) y hemos resuelto el sistema ![]() , siendo
, siendo 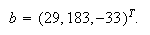 La
solución exacta es
La
solución exacta es ![]() . En cada una de las cinco
perturbaciones realizadas al menos una de las componentes del vector solución ha
variado en más de
. En cada una de las cinco
perturbaciones realizadas al menos una de las componentes del vector solución ha
variado en más de ![]() veces, incluso ha cambiado
de signo. Concretamente, si la matriz perturbada es
veces, incluso ha cambiado
de signo. Concretamente, si la matriz perturbada es  entonces
entonces ![]() .
.
Ni que decir tiene que en un caso como el anterior cualquier error pequeño en los coeficientes del sistema puede llevarnos a una solución completamente errónea.
Bibliografía
A. Aubanell, A. Benseny, A. Delshams, Útiles Básicos de Cálculo Numérico, Labor, Barcelona, 1993.
W. Gautschi, Numerical Analysis. An Introduction, Birkhäuser,1997.
J. Martínez, A, Martínez y A. Lirola, Errores de redondeo: problemas y soluciones, Revista de Informática y Automática, Julio de 1985.
J. H Mathews and K. D. Fink, Métodos Numéricos con Matlab, Prentice Hall, 1999