Integral de Riemann
Francisco Javier Pérez González
Departamento de Análisis Matemático
Universidad de Granada
Un poco de historia
El cálculo integral tiene sus orígenes en problemas de cuadraturas en los que se trataba de calcular áreas de regiones planas limitadas por una o varias curvas. Se atribuye a Eudoxo (ca. 370 A.C.) la invención del método de exhausción, una técnica para calcular el área de una región aproximándola por una sucesión de polígonos de forma que en cada paso se mejorara la aproximación anterior. Arquímides (287-212 A.C.) perfeccionó este método y, entre otros resultados, calculó el área de un segmento de parábola y el volumen de un segmento de paraboloide, así como el área y el volumen de una esfera.
Sorprende que, siendo tan antiguos sus orígenes, la primera definición matemática de integral no fuera dada hasta el siglo XIX por Augustin Louis Cauchy (1789-1857). Una posible explicación es que, durante los siglos XVII y XVIII, la integración fue considerada como la operación inversa de la derivación; el cálculo integral consistía esencialmente en el cálculo de primitivas. Naturalmente, se conocía la utilidad de las integrales para calcular áreas y volúmenes, pero los matemáticos de la época consideraban estas nociones como dadas de forma intuitiva y no vieron la necesidad de precisar su significación matemática. Los trabajos de Joseph Fourier (1768-1830) sobre representación de funciones por series trigonométricas hicieron que el concepto de función evolucionara, desde la idea restrictiva de función como fórmula, hasta la definición moderna de función dada por Dirichlet en 1837. Para entender el significado de la integral de estas nuevas funciones más generales se vio la necesidad de precisar matemáticamente los conceptos de área y de volumen. La originalidad de Cauchy es que unió dos ideas, la de límite y la de área, para dar una definición matemática de integral. Poco después Georg F.B. Riemann (1826-1866) generalizó la definición de integral dada por Cauchy. La teoría de la integral de Riemann fue un avance importante pero insuficiente. Hubo que esperar hasta el siglo XX para que Henri Lebesgue (1875-1941) estableciera en su libro Leçons sur l'intégration et la recherché des fonctions primitives (1904) los fundamentos de una teoría satisfactoria de la integración.
La integración es una de las herramientas más versátiles del Cálculo, sus aplicaciones no se limitan a calcular áreas de regiones planas o volúmenes de sólidos, también se utiliza para calcular longitudes de curvas, centros de masas, momentos de inercia, áreas de superficies, para representar magnitudes físicas como el trabajo, la fuerza ejercida por una presión, o la energía potencial en un campo de fuerzas. Puede decirse que la integración es la herramienta por excelencia para medir; de hecho, las modernas teorías de la integral se llaman teorías de la medida y constituyen el fundamento de ramas de la Matemática como el Cálculo de Probabilidades y la Estadística.
En este curso vamos a estudiar la integración desde un punto de vista esencialmente práctico, evitando largos desarrollos teóricos. Nos interesa la integral como herramienta de cálculo. El curso próximo cuando estudies la integral y la medida de Lebesgue verás que la integración es la herramienta teórica indispensable para obtener algunos de los resultados más profundos del Análisis Matemático.
Para trabajar en este cuaderno debes evaluar primero ( Kernel→ Evaluation→ Evaluate Initialization ) las celdas de inicialización que siguen.
Sumas de Riemann
Sea f:[a,b]→R una función acotada. Representaremos por G(f,a,b) la región del plano comprendida entre la curva y= f(x), el eje de abscisas y las rectas y=a, y=b.
Ejemplos
Puedes representar la región G(f,a,b) (en color amarillo) con la orden graford[f[x],{x,a,b},opts] que admite optciones como "Plot". Prueba con distintas funciones.
![]()
![[Graphics:HTMLFiles/index_13.gif]](HTMLFiles/index_13.gif)
![]()
![[Graphics:HTMLFiles/index_15.gif]](HTMLFiles/index_15.gif)
Nos proponemos calcular el área de dicha región. Puesto que, en general, G(f,a,b) no puede descomponerse en triángulos o rectángulos, no hay una fórmula que nos permita calcular directamente su área. En situaciones como esta, una estrategia básica consiste en obtener soluciones aproximadas que permitan definir el valor exacto del área como límite de las mismas. Fíjate que, al proceder así, estamos definiendo dicho valor exacto, es decir, estamos dando una definición matemática del concepto intuitivo de área. Ello trae como consecuencia inevitable que haya regiones extrañas en el plano que, según la definición dada, no tengan área. Naturalmente, queremos que dicha definición sea lo más general posible, lo que depende del tipo de soluciones aproximadas que elijamos. Las aproximaciones consideradas en la teoría de la integral de Lebesgue conducen a un concepto de área muy general que tendrás oportunidad de estudiar el curso próximo. En lo que sigue vamos a considerar las aproximaciones que conducen a la integral de Riemann.
La integral de Riemann, aunque desde un punto de vista teórico no es hoy día muy interesante, es una herramienta muy útil para calcular y, no lo olvidemos, ese es un objetivo principal en este curso de Cálculo.
Como los conceptos que vamos a introducir se interpretan con más facilidad cuando la función f es positiva, es conveniente tener bien presente en lo que sigue el siguiente artificio que permite representar cualquier función como diferencia de dos funciones positivas.
Parte positiva y parte negativa de una función
Cualquier función f puede escribirse como diferencia de dos funciones positivas:
f(x)=![]() -
-![]() =
=![]() (x)-
(x)-![]() (x)
(x)
la función ![]() (x)=
(x)=![]() se llama parte positiva de f, y la función
se llama parte positiva de f, y la función ![]() (x)=
(x)=![]() se llama parte negativa de f. Si f(x)≥0 se tiene que f(x)=
se llama parte negativa de f. Si f(x)≥0 se tiene que f(x)=![]() (x) y
(x) y ![]() (x)=0; mientras que si f(x)≤0 se tiene que f(x)=-
(x)=0; mientras que si f(x)≤0 se tiene que f(x)=-![]() (x) y
(x) y ![]() (x)=0. Fíjate que, a pesar de su nombre y de la forma en que se simboliza, la función
(x)=0. Fíjate que, a pesar de su nombre y de la forma en que se simboliza, la función ![]() es una función positiva. También es consecuencia de las definiciones dadas que |f(x)|=
es una función positiva. También es consecuencia de las definiciones dadas que |f(x)|=![]() (x)+
(x)+![]() (x), es decir, |f|=
(x), es decir, |f|=![]() +
+![]() .
.
Puedes representar simultáneamente las gráficas de f, ![]() ,
, ![]() y |f| con la orden "Show[graficas, opciones]". Para ello conviene que especifiques, con la opción "PlotRange->{ymin,ymax}", un intervalo común del eje de ordenadas donde se representarán las gráficas. Experimenta con distintas funciones.
y |f| con la orden "Show[graficas, opciones]". Para ello conviene que especifiques, con la opción "PlotRange->{ymin,ymax}", un intervalo común del eje de ordenadas donde se representarán las gráficas. Experimenta con distintas funciones.
![]()
![]()
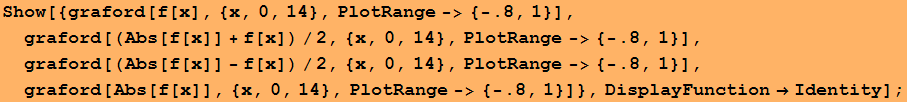
![]()
![[Graphics:HTMLFiles/index_39.gif]](HTMLFiles/index_39.gif)
![[Graphics:HTMLFiles/index_40.gif]](HTMLFiles/index_40.gif)
![[Graphics:HTMLFiles/index_41.gif]](HTMLFiles/index_41.gif)
![[Graphics:HTMLFiles/index_42.gif]](HTMLFiles/index_42.gif)
En lo que sigue, representaremos el valor exacto (que aún no hemos definido) del área de la región G(f,a,b) por λ(G(f,a,b)), (la letra "λ" alude a la inicial de "Lebesgue").
En la integral de Riemann, el área buscada se aproxima por rectángulos de la siguiente forma. Primero, se divide el intervalo [a,b] en un número finito de subintervalos [![]() ,
,![]() ], 1≤ k≤ n, cuyas longitudes pueden ser distintas y con la única condición de que no se solapen: a=
], 1≤ k≤ n, cuyas longitudes pueden ser distintas y con la única condición de que no se solapen: a=![]() <
<![]() <
<![]() < ... <
< ... <![]() <
<![]() =b; se dice que estos puntos constituyen una partición de [a,b]. A continuación se elige en cada subintervalo un punto
=b; se dice que estos puntos constituyen una partición de [a,b]. A continuación se elige en cada subintervalo un punto ![]() ∈[
∈[![]() ,
,![]() ], y se forma el rectángulo cuya base es el intervalo [
], y se forma el rectángulo cuya base es el intervalo [![]() ,
,![]() ] y altura igual a f(
] y altura igual a f(![]() ). Dicho rectángulo está en el semiplano superior si f(
). Dicho rectángulo está en el semiplano superior si f(![]() )≥0 y en el semiplano inferior si f(
)≥0 y en el semiplano inferior si f(![]() )<0. Finalmente se forma la suma
)<0. Finalmente se forma la suma ![]() f(
f(![]() )(
)(![]() -
-![]() ).
).
Definición
Dada una partición P={![]() =a,
=a, ![]() ,
, ![]() ,...,
,..., ![]() ,
,![]() =b} del intervalo [a,b], y un punto
=b} del intervalo [a,b], y un punto ![]() ∈[
∈[![]() ,
,![]() ] en cada uno de los intervalos de la misma, el número
] en cada uno de los intervalos de la misma, el número
![σ(f, P) = Underoverscript[∑, k = 1, arg3] f(t_k) (x_k - x_ (k - 1))](HTMLFiles/index_70.gif)
se llama una suma de Riemann de f para la partición P.
Observaciones
● Fíjate que, como hay libertad para elegir los puntos ![]() ∈[
∈[![]() ,
,![]() ], para cada partición hay infinitas sumas de Riemann.
], para cada partición hay infinitas sumas de Riemann.
● Cuando la función f es positiva, σ(f,P) es una aproximación del área de la región G(f,a,b). Simbólicamente λ(G(f,a,b))=σ(f,P) .
● Cuando la función f toma valores positivos y negativos podemos escribir:![]() f(
f(![]() )(
)(![]() -
-![]() )=
)=![]() (
(![]() (
(![]() )-
)-![]() (
(![]() ))(
))(![]() -
-![]() )=
)=![]()
![]() (
(![]() )(
)(![]() -
-![]() )-
)-![]()
![]() (
(![]() )(
)(![]() -
-![]() ).
).
En este caso, σ(f,P) es una aproximación del área de G(![]() ,a,b) menos el área de G(
,a,b) menos el área de G(![]() ,a,b). Simbólicamente σ(f,P)=λ(G(
,a,b). Simbólicamente σ(f,P)=λ(G(![]() ,a,b))- λ(G(
,a,b))- λ(G(![]() ,a,b)).
,a,b)).
Ejemplos
La función "sumariemann[f,{x,a,b,n}]" elige aleatoriamente una partición de [a,b] con n subintervalos; en cada uno de ellos elige aleatoriamente un valor ![]() , dibuja la gráfica de f y representa, en azul, los rectángulos cuya base es el subintervalo [
, dibuja la gráfica de f y representa, en azul, los rectángulos cuya base es el subintervalo [![]() ,
,![]() ] y altura igual a f(
] y altura igual a f(![]() ) y, en rojo, los puntos (
) y, en rojo, los puntos (![]() ,f(
,f(![]() )). Finalmente, calcula la suma de Riemann correspondiente. Observa que las bases de los rectángulos pueden ser muy distintas entre sí. También puedes comprobar que si ejecutas varias veces el comando, sin cambiar nada en él, obtendrás resultados distintos porque cambiará la partición y los puntos elegidos.
)). Finalmente, calcula la suma de Riemann correspondiente. Observa que las bases de los rectángulos pueden ser muy distintas entre sí. También puedes comprobar que si ejecutas varias veces el comando, sin cambiar nada en él, obtendrás resultados distintos porque cambiará la partición y los puntos elegidos.
![]()
![[Graphics:HTMLFiles/index_106.gif]](HTMLFiles/index_106.gif)
![]()
![[Graphics:HTMLFiles/index_108.gif]](HTMLFiles/index_108.gif)
La función "sumariemannmdelta[f,{x,a,b,n}]" elige aleatoriamente una partición de [a,b] con n subintervalos por la condición de que sus longitudes sean menores que δ=2(b-a)/n, en cada uno de ellos elige aleatoriamente un valor ![]() , dibuja la gráfica de f y representa, en azul, los rectángulos cuya base es el subintervalo [
, dibuja la gráfica de f y representa, en azul, los rectángulos cuya base es el subintervalo [![]() ,
,![]() ] y altura igual a f(
] y altura igual a f(![]() ) y, en rojo, los puntos (
) y, en rojo, los puntos (![]() ,f(
,f(![]() )). Finalmente, calcula la suma de Riemann correspondiente.
)). Finalmente, calcula la suma de Riemann correspondiente.
![]()
![[Graphics:HTMLFiles/index_116.gif]](HTMLFiles/index_116.gif)
![]()
![[Graphics:HTMLFiles/index_118.gif]](HTMLFiles/index_118.gif)
Definición
Dada una partición P={![]() =a,
=a, ![]() ,
, ![]() ,...,
,..., ![]() ,
,![]() =b} del intervalo [a,b], definamos
=b} del intervalo [a,b], definamos ![]() =sup f[
=sup f[![]() ,
,![]() ],
], ![]() =inf f[
=inf f[![]() ,
,![]() ]. Los números
]. Los números
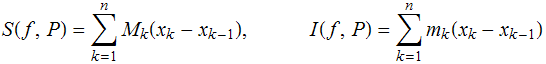
se llaman, respectivamente, suma superior y suma inferior de f para la partición P. Es para definir estas sumas para lo que se precisa que f esté acotada en [a,b]. Puesto que para todo ![]() ∈[
∈[![]() ,
,![]() ] es
] es ![]() ≤f(
≤f(![]() )≤
)≤![]() , deducimos que para toda suma de Riemann, σ(f, P) , de f para la partición P se cumple que I(f,P)≤σ(f,P)≤S(f,P).
, deducimos que para toda suma de Riemann, σ(f, P) , de f para la partición P se cumple que I(f,P)≤σ(f,P)≤S(f,P).
Observaciones
● Para cada partición hay una única suma superior y otra inferior.
● Cuando f es positiva S(f,P) es un valor aproximado por exceso de λ(G(f,a,b)), y I(f,P) es un valor aproximado por defecto de λ(G(f,a,b)).
● Cuando la función f toma valores positivos y negativos S(f,P) es un valor aproximado por exceso de λ(G(![]() ,a,b))-λ(G(
,a,b))-λ(G(![]() ,a,b)), y I(f,P) es un valor aproximado por defecto de λ(G(
,a,b)), y I(f,P) es un valor aproximado por defecto de λ(G(![]() ,a,b))-λ(G(
,a,b))-λ(G(![]() ,a,b)).
,a,b)).
Ejemplos
La función "sumasup[f,{x,a,b,n}, opts]" (que tiene opciones como "Show") divide el intervalo [a,b] en n subintervalos de igual longitud; en cada uno de ellos calcula de forma "casi exacta" un punto ![]() tal que f(
tal que f(![]() )=
)=![]() , dibuja la gráfica de f y representa, en azul, los rectángulos cuya base es el subintervalo [
, dibuja la gráfica de f y representa, en azul, los rectángulos cuya base es el subintervalo [![]() ,
,![]() ] y altura igual a
] y altura igual a ![]() y, en rojo, los puntos (
y, en rojo, los puntos (![]() ,f(
,f(![]() )). Finalmente, calcula la suma superior correspondiente.
)). Finalmente, calcula la suma superior correspondiente.
![]()
![[Graphics:HTMLFiles/index_150.gif]](HTMLFiles/index_150.gif)
![]()
![[Graphics:HTMLFiles/index_152.gif]](HTMLFiles/index_152.gif)
Significado análogo tiene la función "sumainf[f,{x,a,b,n}, opts]".
![]()
![[Graphics:HTMLFiles/index_154.gif]](HTMLFiles/index_154.gif)
![]()
![[Graphics:HTMLFiles/index_156.gif]](HTMLFiles/index_156.gif)
Definición y propiedades básicas de la integral
Supongamos que la función f es positiva en [a,b] . Es claro que, en tal caso, el valor exacto del área de la región G(f,a,b), debe verificar que I(f,P)≤λ(G(f,a,b))≤S(f,P) para toda partición P de [a,b]. Tenemos, en consecuencia, DOS candidatos para λ(G(f,a,b)), a saber:
λ(G(f,a,b))=inf{S(f,P): P ε ℘(a,b)}, y λ(G(f,a,b))=sup{I(f,P): P ε ℘(a,b)}
Donde hemos representado por ℘(a,b) el conjunto de todas las particiones de [a,b]. Llegados aquí, podemos ya dar la definición principal de la teoría de la integral de Riemann.
Definición
Sea f:[a,b]→R una función acotada y positiva en [a,b]. Se dice que el conjunto G(f,a,b) tiene área cuando
inf{S(f,P): P ε ℘(a,b)} =sup{I(f,P): P ε ℘(a,b)}
Dicho valor común es, por definición, el valor del área y lo representaremos por λ(G(f,a,b)). Cuando esto ocurre, se dice también que la función f es integrable Riemann en [a,b] y, por definición, la integral de f en [a,b] es igual a λ(G(f,a,b)):
![]()
En el caso general en que la función f toma valores positivos y negativos, se dice que f es integrable Riemann en [a,b] cuando lo son las funciones ![]() y
y ![]() , en cuyo caso se define la integral de f en [a,b] como el número:
, en cuyo caso se define la integral de f en [a,b] como el número:
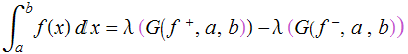
Observaciones
● La definición anterior debes entenderla como una primera aproximación matemática al concepto intuitivo de área. Aunque pueda parecerte extraño, el concepto de área (y de integral) que acabamos de definir es bastante restrictivo.
● En el caso en que la función f toma valores positivos y negativos, observa que la gráfica de ![]() se obtiene por simetría respecto al eje de abscisas de las partes de la gráfica de f en las que f(x)<0. Como regiones simétricas respecto de una recta tienen la misma área, se sigue que:
se obtiene por simetría respecto al eje de abscisas de las partes de la gráfica de f en las que f(x)<0. Como regiones simétricas respecto de una recta tienen la misma área, se sigue que:
λ(G(f,a,b))= λ(G(![]() ,a,b))+λ(G(
,a,b))+λ(G(![]() ,a,b)) =λ(G(
,a,b)) =λ(G(![]() +
+![]() ,a,x)) = λ(G(|f |,a,x))=
,a,x)) = λ(G(|f |,a,x))=![]() |f(x)|dx .
|f(x)|dx .
Seamos prácticos. ¿Cómo podemos, a partir de la definición dada anteriormente, calcular ![]() f(x)dx? Una primera idea en este sentido consiste en observar que cuanto mayor sea el número de intervalos de la partición y más pequeña la anchura de cada uno de ellos cabe esperar que la aproximación obtenida sea mejor. Para precisar esta idea, definimos el paso de una partición P, y lo representamos por δ(P), como la mayor de las longitudes de los subintervalos de dicha partición.
f(x)dx? Una primera idea en este sentido consiste en observar que cuanto mayor sea el número de intervalos de la partición y más pequeña la anchura de cada uno de ellos cabe esperar que la aproximación obtenida sea mejor. Para precisar esta idea, definimos el paso de una partición P, y lo representamos por δ(P), como la mayor de las longitudes de los subintervalos de dicha partición.
Puedes comprobar que, efectivamente, al ir disminuyendo δ(P) la aproximación obtenida va mejorando. Ejecuta los comandos siguientes para ver las respectivas animaciones.
![]()
![[Graphics:HTMLFiles/index_181.gif]](HTMLLinks/sumasup1.gif)
![]()
![[Graphics:HTMLFiles/index_195.gif]](HTMLLinks/sumainf1.gif)
![]()
![[Graphics:HTMLFiles/index_209.gif]](HTMLLinks/sumainf2.gif)
![]()
![[Graphics:HTMLFiles/index_223.gif]](HTMLLinks/sumasup2.gif)
![]()
![[Graphics:HTMLFiles/index_237.gif]](HTMLLinks/sumariemann1.gif)
![]()
![[Graphics:HTMLFiles/index_251.gif]](HTMLLinks/sumainf3.gif)
¿Convencido? No debe extrañarte por ello el siguiente resultado.
Teorema (Convergencia de las sumas integrales)
Sea f:[a,b]→R una función integrable, {![]() } una sucesión de particiones de [a,b] tal que δ(
} una sucesión de particiones de [a,b] tal que δ(![]() )→0 y σ(f,
)→0 y σ(f,![]() ) una suma de Riemann de f para la partición
) una suma de Riemann de f para la partición ![]() . Se verifica entonces que:
. Se verifica entonces que:
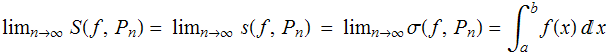
Este resultado permite en algunos casos particulares y con bastante esfuerzo e ingenio calcular ciertas integrales. Como más adelante aprenderemos a calcular integrales con facilidad, es más interesante usar dicho resultado sensu contrario para calcular los límites de ciertas sucesiones.
Pues bien, ha llegado el momento de preguntarse por condiciones que garanticen que una función es integrable Riemann. Nos vamos a contentar con una respuesta parcial a esta pregunta, que es suficiente para nuestros propósitos.
Teorema (Condiciones suficientes de integrabilidad Riemann)
Sea f:[a,b]→R. Cada una de las siguientes condiciones garantizan que f es integrable Riemann en [a,b]:
i) f está acotada en [a,b] y tiene un número finito de discontinuidades en [a,b]. En particular, toda función continua en un intervalo cerrado y acotado es integrable en dicho intervalo.
ii) f es monótona en [a,b].
La demostración de este resultado, que no vamos a dar, consiste, en cada caso, en probar que dado un número ε>0, hay una partición P del intervalo [a,b] tal que S(P,f) - s(P,f)<ε.
Teniendo en cuenta que σ(αf+βg,P)=ασ(f,P)+βσ(g,P), cualesquiera sean las funciones f, g y los números α, β, se deduce, haciendo uso del resultado sobre convergencia de sumas integrales, que la integral es lineal. Esta propiedad, junto con otras propiedades básicas de las integrales se recogen en el siguiente resultado.
Teorema (Propiedades básicas de la integral)
i) Linealidad. Si f,g son integrables en [a,b] y α, β son números reales, se verifica que la función αf + βg también es integrable en [a,b] y:
![]() (α f(x)+β g(x))dx=α
(α f(x)+β g(x))dx=α![]() f(x)dx + β
f(x)dx + β ![]() g(x)dx.
g(x)dx.
ii) Conservación del orden. Si f,g son integrables en [a,b] y f(x)≤ g(x) para todo x en [a,b], entonces se verifica que:
![]() f(x)dx ≤
f(x)dx ≤ ![]() g(x)dx
g(x)dx
En particular, si f es integrable en [a,b] y m≤f(x)≤M para todo x en [a,b], entonces se verifica la siguiente acotación fundamental:
m(b-a) ≤ ![]() f(x)dx ≤ M(b-a)
f(x)dx ≤ M(b-a)
iii) Si f es integrable en [a,b] también | f | (función valor absoluto de f) es integrable en [a,b] y se verifica la desigualdad:
|![]() f(x)dx |≤
f(x)dx |≤ ![]() |f(x)|dx
|f(x)|dx
iv) El producto de funciones integrables Riemann también es una función integrable Riemann.
v) Aditividad respecto del intervalo. Sea a < c < b. Una función f es integrable en [a,b] si, y sólo si, es integrable en [a,c] y en [c,b], en cuyo caso se verifica la igualdad:
![]() f(x)dx=
f(x)dx=![]() f(x)dx+
f(x)dx+![]() f(x)dx
f(x)dx
El Teorema Fundamental del Cálculo
Dada una función integrable f:[a,b]→R podemos definir una nueva función F:[a,b]→R por F(x)=![]() f(t)dt para todo x ε [a,b]. Nuestro próximo objetivo va a ser estudiar dicha función. Recuerda que F(x)=λ(G(
f(t)dt para todo x ε [a,b]. Nuestro próximo objetivo va a ser estudiar dicha función. Recuerda que F(x)=λ(G(![]() ,a,x))-λ(G(
,a,x))-λ(G(![]() ,a,x)). Por supuesto, si f es una positiva entonces F(x)=λ(G(f,a,x)) es el área de la región del plano limitada por la gráfica de f , el eje de abscisas y las rectas y=a, y=x. No debes olvidar en lo que sigue que F(x)=
,a,x)). Por supuesto, si f es una positiva entonces F(x)=λ(G(f,a,x)) es el área de la región del plano limitada por la gráfica de f , el eje de abscisas y las rectas y=a, y=x. No debes olvidar en lo que sigue que F(x)=![]() f(t)dt se ha definido en términos de áreas.
f(t)dt se ha definido en términos de áreas.
El comando "areafunc[f[x], {x, a, b}, n, {ymin, ymax},opts]" (admite opciones como "Show") da como salida n gráficas y en cada una de ellas representa la gráfica de f, la región G(f,a,a+k(b-a)/n) en azul, y la gráfica de F(x)=λ(G(![]() ,a,x))-λ(G(
,a,x))-λ(G(![]() ,a,x)), en rojo, en el intervalo [a,a+k(b-a)/n], para 1≤ k ≤ n. Además, en cada caso da el valor de F(a+k(b-a)/n). Para usar el comando tienes que fijar los valores "ymin" e "ymax" que determinan el intervalo del eje de ordenadas en que se representarán las funciones. Experimenta con distintas funciones y fíjate si la función F(x)=λ(G(
,a,x)), en rojo, en el intervalo [a,a+k(b-a)/n], para 1≤ k ≤ n. Además, en cada caso da el valor de F(a+k(b-a)/n). Para usar el comando tienes que fijar los valores "ymin" e "ymax" que determinan el intervalo del eje de ordenadas en que se representarán las funciones. Experimenta con distintas funciones y fíjate si la función F(x)=λ(G(![]() ,a,x))-λ(G(
,a,x))-λ(G(![]() ,a,x)) te resulta conocida en algunos casos.
,a,x)) te resulta conocida en algunos casos.
![]()
![[Graphics:HTMLFiles/index_290.gif]](HTMLLinks/TFC1.gif)
![]()
![[Graphics:HTMLFiles/index_305.gif]](HTMLLinks/TFC2.gif)
![areafunc[ Sin[x]/x, {x, 0.01, 12}, 10, {-.8, 2.1}] ; SelectionMove[EvaluationNotebook[], All, GeneratedCell] ;](HTMLFiles/index_306.gif)
![[Graphics:HTMLFiles/index_319.gif]](HTMLLinks/TFC3.gif)
![areafunc[Exp[-x^2], {x, -2, 2}, 10, {-.2, 2}, Frame→True, Background→RGBColor[1, .8, .8]] ; SelectionMove[EvaluationNotebook[], All, GeneratedCell] ;](HTMLFiles/index_320.gif)
![[Graphics:HTMLFiles/index_333.gif]](HTMLLinks/TFC4.gif)
A veces puede ser conveniente considerar funciones de la forma F(x)=![]() f(t)dt en donde a < c < b y x ε [a,b] por lo que es necesario precisar lo que se entiende por
f(t)dt en donde a < c < b y x ε [a,b] por lo que es necesario precisar lo que se entiende por ![]() f(t)dt cuando x < c. El convenio que se hace es que
f(t)dt cuando x < c. El convenio que se hace es que ![]() f(t)dt=-
f(t)dt=- ![]() f(t)dt cualquiera sean los números u y v. La justificación de este convenio es que, con él, la igualdad
f(t)dt cualquiera sean los números u y v. La justificación de este convenio es que, con él, la igualdad
![]() f(t)dt+
f(t)dt+![]() f(t)dt+
f(t)dt+![]() f(t)dt=0
f(t)dt=0
se cumple cualesquiera sean los puntos x, y, z del intervalo [a,b]. Compruébalo.
Nuestro próximo objetivo va a consistir en invertir el proceso que nos ha llevado de f a F(x)=![]() f(t)dt. Nuestro problema es: ¿Cómo podemos recuperar la función f a partir del conocimiento de la función área de f, es decir, de la función F? Piensa un poco en las operaciones que hay que realizar sobre f para obtener su función área. Dichas operaciones son: evaluar f en algunos puntos del intervalo, multiplicar dichos valores por las longitudes de subintervalos apropiados, sumar todos estos números y pasar al límite. Todo ello queda reflejado en la igualdad que expresa la convergencia de las sumas de Riemann a la integral:
f(t)dt. Nuestro problema es: ¿Cómo podemos recuperar la función f a partir del conocimiento de la función área de f, es decir, de la función F? Piensa un poco en las operaciones que hay que realizar sobre f para obtener su función área. Dichas operaciones son: evaluar f en algunos puntos del intervalo, multiplicar dichos valores por las longitudes de subintervalos apropiados, sumar todos estos números y pasar al límite. Todo ello queda reflejado en la igualdad que expresa la convergencia de las sumas de Riemann a la integral:
lim ![]() f(
f(![]() )(
)(![]() -
-![]() )=
)=![]() f(t)dt
f(t)dt
Parece razonable que para invertir el proceso anterior, evaluemos F en puntos x, y del intervalo, hagamos la diferencia F(x) - F(y), dividamos por la longitud del intervalo, ![]() , y tomemos límites. Como puedes ver, este proceso nos conduce de forma natural a estudiar la derivada de la función área, F. El resultado que sigue, uno de los más útiles del Cálculo, establece una relación entre dos conceptos aparentemente lejanos entre sí: el concepto de área y el de tangente a una curva.
, y tomemos límites. Como puedes ver, este proceso nos conduce de forma natural a estudiar la derivada de la función área, F. El resultado que sigue, uno de los más útiles del Cálculo, establece una relación entre dos conceptos aparentemente lejanos entre sí: el concepto de área y el de tangente a una curva.
Teorema Fundamental del Cálculo
Sea f:[a,b]→R una función integrable y definamos F:[a,b]→R por F(x)=![]() f(t)dt para todo x en [a,b]. Entonces:
f(t)dt para todo x en [a,b]. Entonces:
i) F es continua en [a,b].
ii) En todo punto c de [a,b] en el que f sea continua se verifica que F es derivable en dicho punto siendo F'(c)=f(c). En particular, si f es continua en [a,b], entonces F es derivable en [a,b] y F'(x)=f(x) para todo x en [a,b].
Demostración.
i) Como f es integrable debe estar acotada. Sea M>0 tal que |f(x)|≤ M para todo x en [a,b]. Entonces, si x < y son puntos de [a,b] tenemos que:
|F(y)-F(x)|=|![]() f(t)dt|≤
f(t)dt|≤![]() |f(t)|dt ≤ M(y-x)
|f(t)|dt ≤ M(y-x)
Por la misma razón, si suponemos que y < x, tendremos que |F(x)-F(y)|≤ M(x-y). Estas dos desigualdades nos dicen que |F(x)-F(y)|≤ M|x-y| para todo par de puntos x, y de [a, b]. De esta desigualdad se sigue inmediatamente la continuidad de F en [a, b].
ii) Pongamos
![]() -f(c)=
-f(c)= ![]() =
=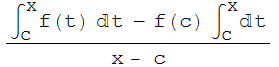 =
=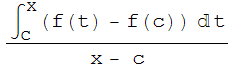
Dado, ε>0, la continuidad de f en c nos dice que hay un δ>0 tal que para todo t ε [a,b] tal que | t - c|<δ se tiene que |f(t)-f(c)|<ε. Tomemos ahora un punto cualquiera x ε [a,b] tal que |x-c|<δ. Entonces es claro que para todo t comprendido entre x y c se tendrá que |t-c|<δ y, por tanto, |f(t)-f(c)|<ε por lo que |![]() (f(t)-f(c))dt|≤ε|x-c|. Deducimos que para todo x ε [a,b] tal que | x - c|<δ, x ≠ c, se verifica que:
(f(t)-f(c))dt|≤ε|x-c|. Deducimos que para todo x ε [a,b] tal que | x - c|<δ, x ≠ c, se verifica que:
|![]() -f(c)|=|
-f(c)|=|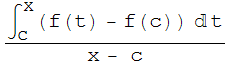 |≤
|≤![]() =ε
=ε
Hemos probado así que ![]()
![]() = f(c), esto es, F es derivable en c y F'(c)=f(c).
= f(c), esto es, F es derivable en c y F'(c)=f(c).
Definición
Dada un función h:[a,b]→R, cualquier función H:[a,b]→R que sea continua en [a,b], derivable en ]a,b[ y verifique que H'(x)=h(x) para todo x ∈ ]a,b[, se llama una primitiva de f en el intervalo [a,b].
Es importante advertir que no todas las funciones tienen primitivas. Una condición necesaria que debe cumplir una función para tener primitivas es que dicha función tenga la propiedad del valor intermedio pues, como recordarás, las funciones derivadas tienen esa propiedad. También, como consecuencia del teorema del valor medio, es inmediato que dos primitivas de una función en un mismo intervalo se diferencian en una constante. Por ello, si conocemos una primitiva de una función en un intervalo las conocemos todas. Precisamente, una consecuencia muy importante del Teorema Fundamental del Cálculo es que toda función continua en un intervalo tiene primitivas en dicho intervalo. Además, el teorema nos dice que la función área, esto es, la función F(x)=![]() f(t)dt es la primitiva de la función continua f:[a,b]→R, que se anula en a, F(a)=0. Es importante que aprecies que este es un teorema de existencia; es la definición que hemos dado de área - y por consiguiente de integral - lo que nos ha permitido construir la función primitiva de f. No lo olvides: la integración es una potente herramienta para construir nuevas funciones.
f(t)dt es la primitiva de la función continua f:[a,b]→R, que se anula en a, F(a)=0. Es importante que aprecies que este es un teorema de existencia; es la definición que hemos dado de área - y por consiguiente de integral - lo que nos ha permitido construir la función primitiva de f. No lo olvides: la integración es una potente herramienta para construir nuevas funciones.
El Teorema Fundamental del Cálculo proporciona una técnica para calcular la integral de una función continua en un intervalo [a,b]. Para ello lo que hacemos es obtener una primitiva de f en [a,b]. Si h es una tal primitiva, entonces las funciones x|→ h(x)-h(a), y x |→ ![]() f(t)dt son dos primitivas de f en [a,b] que coinciden en un punto, pues ambas se anulan en a. Deducimos que
f(t)dt son dos primitivas de f en [a,b] que coinciden en un punto, pues ambas se anulan en a. Deducimos que ![]() f(t)dt = h(x)-h(a), por lo que
f(t)dt = h(x)-h(a), por lo que ![]() f(t)dt = h(b)-h(a). Podemos generalizar este resultado como sigue.
f(t)dt = h(b)-h(a). Podemos generalizar este resultado como sigue.
Regla de Barrow
Sea f:[a,b]→R integrable y supongamos que h es una primitiva de f en [a,b]. Entonces ![]() f(t)dt = h(b)-h(a).
f(t)dt = h(b)-h(a).
Fíjate que en el resultado anterior no se supone que f sea continua sino tan sólo que es integrable y que, además, tiene una primitiva. La idea de la demostración es como sigue. Tomemos una partición P={![]() =a,
=a, ![]() ,
, ![]() ,...,
,..., ![]() ,
,![]() =b}del intervalo [a,b]. Entonces podemos escribir:
=b}del intervalo [a,b]. Entonces podemos escribir:
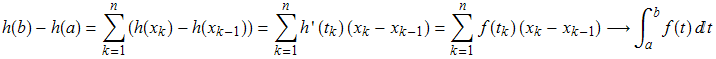
donde hemos usado el teorema del valor medio.
Algunas observaciones sobre el cálculo de integrales
De lo antes dicho, se sigue que para calcular ![]() f(t)dt donde f es una función continua, hay que calcular una primitiva de f, evaluarla en a y en b y hacer la diferencia. Pero, ¿para qué calcular una primitiva? ¿no sabemos ya que una primitiva de f es la función
f(t)dt donde f es una función continua, hay que calcular una primitiva de f, evaluarla en a y en b y hacer la diferencia. Pero, ¿para qué calcular una primitiva? ¿no sabemos ya que una primitiva de f es la función ![]() f(t)dt? Y, naturalmente, cualquier otra será de la forma
f(t)dt? Y, naturalmente, cualquier otra será de la forma ![]() f(t)dt +C donde C es una constante. ¿Qué interés tiene entonces el cálculo de primitivas de funciones continuas? Respuesta: desde un punto de vista teórico ninguno. Ahora, si lo que queremos es calcular el número
f(t)dt +C donde C es una constante. ¿Qué interés tiene entonces el cálculo de primitivas de funciones continuas? Respuesta: desde un punto de vista teórico ninguno. Ahora, si lo que queremos es calcular el número ![]() f(t)dt, entones la "primitiva trivial" de f, esto es, la función F(x)=
f(t)dt, entones la "primitiva trivial" de f, esto es, la función F(x)=![]() f(t)dt, no nos sirve para nada porque si la evaluamos en a y en b y hacemos la diferencia, obtenemos una identidad perfectamente inútil para nuestros propósitos. Lo que necesitamos es conocer una primitiva f que sea realmente evaluable, es decir que al evaluarla en a y en b proporcione valores numéricos. En otros términos, el problema del cálculo de primitivas consiste en tratar de expresar la "primitiva trivial" F(x)=
f(t)dt, no nos sirve para nada porque si la evaluamos en a y en b y hacemos la diferencia, obtenemos una identidad perfectamente inútil para nuestros propósitos. Lo que necesitamos es conocer una primitiva f que sea realmente evaluable, es decir que al evaluarla en a y en b proporcione valores numéricos. En otros términos, el problema del cálculo de primitivas consiste en tratar de expresar la "primitiva trivial" F(x)= ![]() f(t)dt por medio de funciones elementales que permitan una evaluación efectiva de la integral. Para eso sirven las técnicas de cálculo de primitivas. Pero sucede con frecuencia que no hay forma de expresar la función F(x)=
f(t)dt por medio de funciones elementales que permitan una evaluación efectiva de la integral. Para eso sirven las técnicas de cálculo de primitivas. Pero sucede con frecuencia que no hay forma de expresar la función F(x)= ![]() f(t)dt por medio de funciones elementales. Esto ocurre, por ejemplo, cuando f(x)=sen(x)/x o f(x)=exp(
f(t)dt por medio de funciones elementales. Esto ocurre, por ejemplo, cuando f(x)=sen(x)/x o f(x)=exp(![]() ), en tales casos la forma más sencilla de representar una primitiva de f es justamente mediante la función F(x)=
), en tales casos la forma más sencilla de representar una primitiva de f es justamente mediante la función F(x)= ![]() f(t)dt y, para obtener valores concretos de dicha función hay que recurrir a métodos numéricos de cálculo de integrales.
f(t)dt y, para obtener valores concretos de dicha función hay que recurrir a métodos numéricos de cálculo de integrales.
A vueltas con las funciones logaritmo y exponencial
Quiero convencerte de que muchas veces el cálculo integral proporciona la interpretación más ituitiva de una función. Considera, por ejemplo, la función logaritmo natural. Quizás sepas expresar log(2) como límite de una sucesión o algo parecido; pero, ¿puedes representar de alguna forma intuitiva el número log(2)? ¿Sabrías representar gráficamente el número log(2)? Evalúa la siguente celda para ver log(2).
![]()
![[Graphics:HTMLFiles/index_382.gif]](HTMLFiles/index_382.gif)
Espero que estés de acuerdo conmigo: la forma más fácil e intuitiva de imaginar el número log(t) es como el área de la región plana limitada por la curva y=1/x, las rectas y=1, y=t, y el eje de abscisas. Dicha área se considera positiva si t>1y negativa si t<1. Dicho de otra forma, log(t)=![]()
![]() dx. Olvida ahora todo lo que sepas de la función logaritmo natural. ¿Lo has olvidado ya? Pues, bien, ahora vamos a definir la función logaritmo natural como la función log:
dx. Olvida ahora todo lo que sepas de la función logaritmo natural. ¿Lo has olvidado ya? Pues, bien, ahora vamos a definir la función logaritmo natural como la función log:![]() → Rdada por log(x)=
→ Rdada por log(x)=![]()
![]() dt para todo x>0. El Teorema Fundamental del Cálculo nos dice que dicha función es derivable y log'(x)=1/x. Como la derivada es positiva, deducimos que dicha función es estrictamente creciente. Ahora, dado, a>0, sea h(x)=log(a x). Entonces h'(x)=a/a x=1/x; luego la función h(x)-log(x)tiene derivada nula en
dt para todo x>0. El Teorema Fundamental del Cálculo nos dice que dicha función es derivable y log'(x)=1/x. Como la derivada es positiva, deducimos que dicha función es estrictamente creciente. Ahora, dado, a>0, sea h(x)=log(a x). Entonces h'(x)=a/a x=1/x; luego la función h(x)-log(x)tiene derivada nula en ![]() , por lo que es constante y, como para x=1 es igual a log(a), se sigue que h(x)-log(x)=log(a). Hemos probado que log(a x)=log(a)+log(x) para todo x>0 y para todo a>0. Observa que en poco más de tres líneas hemos obtenido ya las propiedades principales del logaritmo. Sigamos nuestro estudio. Como log(
, por lo que es constante y, como para x=1 es igual a log(a), se sigue que h(x)-log(x)=log(a). Hemos probado que log(a x)=log(a)+log(x) para todo x>0 y para todo a>0. Observa que en poco más de tres líneas hemos obtenido ya las propiedades principales del logaritmo. Sigamos nuestro estudio. Como log(![]() )=n log(2) para todo número entero n, deducimos que la función log(x) no está mayorada ni minorada y, como es estrictamente creciente, concluimos que
)=n log(2) para todo número entero n, deducimos que la función log(x) no está mayorada ni minorada y, como es estrictamente creciente, concluimos que ![]() log(x)=-∞ y
log(x)=-∞ y ![]() log(x)=+∞. Por tanto, podemos afirmar que log(x) es una biyección estrictamente creciente de
log(x)=+∞. Por tanto, podemos afirmar que log(x) es una biyección estrictamente creciente de ![]() sobre R. Representemos provisionalmente por φ:R→ R la función inversa del logaritmo. Dicha función se llama función exponencial natural. El teorema de derivación de la inversa nos dice que φ es derivable y φ'(x)=1/log'(φ(x))=φ(x) para todo número real x. Ahora, dados, x,y ∈ R, sean a,b>0 tales que x= log(a), y=log(b). Entonces φ(x+y)=φ(log(a)+log(b))=φ(log(a b))=a b=φ(x)φ(y). De la igualdad φ(x+y)=φ(x)φ(y) se deduce fácilmente que φ(r)=
sobre R. Representemos provisionalmente por φ:R→ R la función inversa del logaritmo. Dicha función se llama función exponencial natural. El teorema de derivación de la inversa nos dice que φ es derivable y φ'(x)=1/log'(φ(x))=φ(x) para todo número real x. Ahora, dados, x,y ∈ R, sean a,b>0 tales que x= log(a), y=log(b). Entonces φ(x+y)=φ(log(a)+log(b))=φ(log(a b))=a b=φ(x)φ(y). De la igualdad φ(x+y)=φ(x)φ(y) se deduce fácilmente que φ(r)=![]() para todo número racional r. El número φ(1) se representa con la letra e, es decir, es el número definido por la igualdad log(e)=
para todo número racional r. El número φ(1) se representa con la letra e, es decir, es el número definido por la igualdad log(e)=![]()
![]() dt=1. Con ello φ(r)=
dt=1. Con ello φ(r)=![]() para todo número racional r, por lo que se usa la notación φ(x)=
para todo número racional r, por lo que se usa la notación φ(x)=![]() para representar a la función exponencial.
para representar a la función exponencial.
Fíjate con qué facilidad y elegancia hemos obtenido las propiedades principales de las funciones logaritmo y exponencial naturales. La definición que hemos dado de la función logaritmo tiene también la ventaja de que algunas desigualdades resultan gráficamente evidentes.Por ejemplo, la desigualdad 1/2+1/3+...+1/n≤ log n≤ 1+1/2+...+1/(n-1). Las gráficas siguientes son una demostración sin palabras de la desigualdad anterior para n=8.
![]()
![[Graphics:HTMLFiles/index_399.gif]](HTMLFiles/index_399.gif)
![[Graphics:HTMLFiles/index_400.gif]](HTMLFiles/index_400.gif)
Integrales de funciones no acotadas o en intervalos no acotados
¿Es posible asignar área a una región no acotada del plano? A primera vista, puede parecer que cualquier región no acotada del plano (coloquialmente hablando, una región infinita o ilimitada) debe tener área infinita. Una primera reflexión te convencerá de que eso no tiene por qué ser así. Por ejemplo, recuerda que arctg(x)=![]()
![]() dt y
dt y ![]() arctg(x)=π/2. Parece por tanto razonable definir
arctg(x)=π/2. Parece por tanto razonable definir ![]()
![]() dt=π/2 e interpretar dicha integral como el área de la región no acotada del plano comprendida entre la curva y=
dt=π/2 e interpretar dicha integral como el área de la región no acotada del plano comprendida entre la curva y=![]() y el semieje positivo x≥0. Otro ejemplo más evidente: considera la región del plano Ω formada por la unión de los rectángulos
y el semieje positivo x≥0. Otro ejemplo más evidente: considera la región del plano Ω formada por la unión de los rectángulos ![]() que tienen como base el intervalo [n,n+1] y altura 1/
que tienen como base el intervalo [n,n+1] y altura 1/![]() , donde n es un número natural. Evidentemente, se trata de una región no acotada. Parece lógico definir su área como el ímite:
, donde n es un número natural. Evidentemente, se trata de una región no acotada. Parece lógico definir su área como el ímite:
λ(Ω)=![]() (λ(
(λ(![]() )+λ(
)+λ(![]() )+...+λ(
)+...+λ(![]() ))=
))= ![]() (1/2+1/4+...+1/
(1/2+1/4+...+1/![]() )=1
)=1
Seguro que ahora se te ocurren otros ejemplos. Pues bien, nuestro objetivo va a consistir en asignar área a regiones del plano no acotadas de la forma G(f,a,b) donde -∞≤a<b≤+∞, y f es una función continua en el intervalo de extremos a y b. Se trata, naturalmente, de la región del plano comprendida entre la curva y=f(x) y el intervalo del eje de abscisas de extremos a y b. Recuerda que toda función continua en un intervalo cerrado y acotado está acotada en dicho intervalo, por lo que la región G(f,a,b) será no acotada cuando ocurra una o las dos posibles situaciones siguientes:
i) a=-∞, o b=+∞; es decir, el intervalo de extremos a y b, no está acotado: es una semirecta o toda la recta real;
ii) La función f no está acotada.
La consideración por separado de cada uno de los casos que pueden darse sería repetitiva y aburrida; es posible, sin embargo, reducir esencialmente todas las posibilidades a una sola. Para ello, observa que si a<c<b entonces G(f,a,b)=G(f,a,c)∪G(f,c,b) por lo que es suficiente para nuestros propósitos considerar intervalos del tipo ]a,c] o [c,b[ donde c es un número real y -∞≤a, b ≤+∞. Como la teoría resultante en ambos casos es totalmente simétrica, consideraremos en lo que sigue solamente intervalos de tipo [c,b[ donde c es un número real y b es un número real mayor que c o bien b=+∞, dejando como ejercicio la traducción para intervalos del tipo ]a,c] de las definiciones y resultados que siguen.
Definición
Sea f continua en [c,b[. Si existe y es finito el límite ![]()
![]() f(t)dt se dice que la integral de f es convergente en [c,b[. En tal caso, se define la integral de f en [c,b[ como el número:
f(t)dt se dice que la integral de f es convergente en [c,b[. En tal caso, se define la integral de f en [c,b[ como el número:
![]() f(x)dx=
f(x)dx= ![]()
![]() f(t)dt
f(t)dt
Cuando dicho límite no existe se dice que la integral de f no es convergente en [c,b[. En los casos en que ![]()
![]() f(t)dt=-∞, o
f(t)dt=-∞, o ![]()
![]() f(t)dt=+∞, se dice que la integral de f es negativamente, o positivamente, divergente en [c,b[ y, simbólicamente, escribimos
f(t)dt=+∞, se dice que la integral de f es negativamente, o positivamente, divergente en [c,b[ y, simbólicamente, escribimos ![]() f(t)dt=-∞, o
f(t)dt=-∞, o ![]() f(t)dt=+∞.
f(t)dt=+∞.
Obervaciones sobre la terminología usual
Las integrales que acabamos de definir se llaman integrales impropias de Riemann. En este sentido se habla usualmente de la convergencia de la integral impropia de Riemann o del "valor de la integral impropia de Riemann" o se dice que "f es impropiamente integrable Riemann". Es bueno que conozcas esta terminología porque es la que emplean casi todos los textos, pero no olvides que es tan sólo una manera de hablar y que los conceptos a los que se refiere son los que acabamos de definir. En mi opinión esta terminología es bastante farragosa e innecesaria por lo que, en adelante, no la usaremos.
Según la definición anterior, para estudiar la convergencia de una integral basta con estudiar el límite de una primitiva de f, pues eso es la función F(x)= ![]() f(t)dt. Si f tiene en el intervalo [c,b[ una primitiva, F, que se expresa por medio de funciones elementales, y tenemos la suerte de conocerla, es posible calcular, con las técnicas usuales, el valor del límite
f(t)dt. Si f tiene en el intervalo [c,b[ una primitiva, F, que se expresa por medio de funciones elementales, y tenemos la suerte de conocerla, es posible calcular, con las técnicas usuales, el valor del límite ![]() F(x). Veamos algunos ejemplos.
F(x). Veamos algunos ejemplos.
Ejemplos
i) Si α≠-1, ![]()
![]() dt =
dt = ![]() -
- ![]() . Deducimos que si α+1<0
. Deducimos que si α+1<0 ![]()
![]() dt=
dt=![]()
![]()
![]() dt=-
dt=-![]() , y si α+1>0 entonces
, y si α+1>0 entonces ![]()
![]() dt=+∞.
dt=+∞.
Análogamente, si α+1>0 es ![]()
![]() dt =
dt = ![]()
![]()
![]() dt=
dt=![]() , y si α+1<0 es
, y si α+1<0 es ![]()
![]() dt =+∞.
dt =+∞.
ii) Usando la técnica de integración por partes, que estudiaremos más adelante, es fácil calcular una primitiva de la función
f(x)=![]() log x donde α≠-1. Comprueba que F(x)=
log x donde α≠-1. Comprueba que F(x)=![]() es una primitiva de f(x) en
es una primitiva de f(x) en ![]() . Por tanto
. Por tanto ![]()
![]() log tdt = F(x) -F(1). En consecuencia, si α+1<0 es
log tdt = F(x) -F(1). En consecuencia, si α+1<0 es ![]()
![]() log tdt =-F(1)=
log tdt =-F(1)=![]() , y si α+1>0 entonces
, y si α+1>0 entonces ![]()
![]() log tdt =+∞.
log tdt =+∞.
Análogamente, si α+1>0 es ![]()
![]() log tdt =
log tdt = ![]() (F(1)-F(x))=F(1)=-
(F(1)-F(x))=F(1)=-![]() , y si α+1<0 es
, y si α+1<0 es ![]()
![]() log tdt =-∞.
log tdt =-∞.
Mathematica conoce estos resultados como puedes comprobar con la orden Integrate[f[x],{x,a,b}] que calcula la integral de la función f en el intervalo de extremos a y b. Cuando la función f tiene además de la variable un parámetro, Mathematica da el resultado más general imponiendo, si es necesario, condiciones sobre el parámetro. En esta situación también podemos informar a Mathematica de que el parámetro satisface ciertas condiciones previas; por ejemplo, que es un número real (por defecto, Mathematica trata los parámetros como números complejos).
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Naturalmente, no siempre vamos a disponer de una primitiva expresable por medio de funciones elementales, bien porque no exista o porque su cálculo efectivo sea muy complicado. Por ello, interesa conocer condiciones que aseguren la convergencia de una integral sin necesidad de conocer una primitiva elemental. Lógicamente, estas condiciones no nos permitarán calcular el valor numérico de la integral; tan sólo nos dirán si es o no convergente. El caso en que la función integrando es positiva es particularmente sencillo de estudiar.
Criterio básico de convergencia
Sea f continua y positiva en [c,b[. Entonces, la integral de f en [c,b[ es convergente si, y sólo si, la función F(x)= ![]() f(t)dt está mayorada en [c,b[, en cuyo caso
f(t)dt está mayorada en [c,b[, en cuyo caso ![]() f(x)dx=sup{
f(x)dx=sup{![]() f(t)dt:c≤x<b }. En otro caso la integral de f en [c,b[ es positivamente divergente.
f(t)dt:c≤x<b }. En otro caso la integral de f en [c,b[ es positivamente divergente.
La afirmación anterior es consecuencia de que por ser f positiva la función F(x)= ![]() f(t)dt es creciente. El siguiente criterio de convergencia es consecuencia fácil del anterior.
f(t)dt es creciente. El siguiente criterio de convergencia es consecuencia fácil del anterior.
Criterio de comparación
Sean f y g continuas y positivas en [c,b[. Supongamos que la integral de g en [c,b[ es convergente y que f(x)≤g(x) para todo x en [c, b[. Entonces la integral de f en [c,b[ también es convergente.
Criterio límite de comparación
Sean f y g continuas y positivas en [c,b[. Supongamos que ![]()
![]() =λ≠0. Entonces las integrales de f y g en [c,b[ ambas convergen o ambas divergen positivamente.
=λ≠0. Entonces las integrales de f y g en [c,b[ ambas convergen o ambas divergen positivamente.
Definición
Sea f continua en ]a,b[ donde -∞≤a<b≤+∞, y sea c∈]a,b[. Si la integral de f es convergente en [c,b[ y en ]a,c], se dice que la integral de f es convergente en ]a,b[ y se define su valor como el número ![]() f(x)dx=
f(x)dx=![]() f(x)dx+
f(x)dx+![]() f(x)dx. En el caso de que alguna de las integrales de f en ]a,c] o en [c,b[ no sea convergente se dice que la integral de f no es convergente en ]a,b[. En el caso de que las integrales de f en ]a,c] y en [c,b[ sean ambas positivamente divergentes o una convergente y otra positivamente divergente, se dice que la integral de f es positivamente divergente en ]a,b[ y, simbólicamente, escribimos
f(x)dx. En el caso de que alguna de las integrales de f en ]a,c] o en [c,b[ no sea convergente se dice que la integral de f no es convergente en ]a,b[. En el caso de que las integrales de f en ]a,c] y en [c,b[ sean ambas positivamente divergentes o una convergente y otra positivamente divergente, se dice que la integral de f es positivamente divergente en ]a,b[ y, simbólicamente, escribimos ![]() f(t)dt=+∞. Análogo significado tiene la expresión
f(t)dt=+∞. Análogo significado tiene la expresión ![]() f(t)dt=-∞.
f(t)dt=-∞.
Ejemplos
i) ![]()
![]() dx=
dx=![]()
![]() dx+
dx+![]()
![]() dx =
dx = ![]()
![]()
![]() dx +
dx + ![]()
![]()
![]() dx =
dx =
= ![]() (arctg 0 -arctag t) +
(arctg 0 -arctag t) + ![]() (arctg s -arctag 0) =π/2 + π/2=π .
(arctg s -arctag 0) =π/2 + π/2=π .
ii) 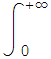
![]() dx=
dx=![]()
![]() dx+
dx+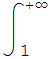
![]() dx=+∞ porque una de las dos integrales converge y la otra diverge positivamente.
dx=+∞ porque una de las dos integrales converge y la otra diverge positivamente.
iii) ![]()
![]() dx=
dx=![]()
![]() dx+
dx+![]()
![]() dx=
dx=![]()
![]()
![]() dx+
dx+![]()
![]()
![]() dx=
dx=
=![]() (arcsen 0 -arcsen t)+
(arcsen 0 -arcsen t)+![]() (arcsen s - arcsen 0)=π/2 + π/2=π .
(arcsen s - arcsen 0)=π/2 + π/2=π .
Definición
Es fácil ahora asociar área a regiones no acotadas del plano de la forma G(f,c,b)donde -∞<c<b≤+∞ y f es una función continua en el intervalo [c,b[. Para ello, basta tomar límites en la igualdad λ(G(f,c,t))=![]() |f(x)|dx. Llegamos así a la definición λ(G(f,c,b))=
|f(x)|dx. Llegamos así a la definición λ(G(f,c,b))=![]() |f(x)|dx. En el caso de una región del tipo G(f,a,b), como la considerada en la definición anterior, basta tener en cuenta que si a<c<b es G(f,a,b)=G(f,a,c)∪G(f,c,b) por lo que definimos, λ(G(f,a,b))=
|f(x)|dx. En el caso de una región del tipo G(f,a,b), como la considerada en la definición anterior, basta tener en cuenta que si a<c<b es G(f,a,b)=G(f,a,c)∪G(f,c,b) por lo que definimos, λ(G(f,a,b))=![]() |f(x)|dx+
|f(x)|dx+![]() |f(x)|dx=
|f(x)|dx=![]() |f(x)|dx.
|f(x)|dx.
Si la función f toma valores positivos y negativos, puede ocurrir que la integral de f sea convergente y la integral de la función | f | no lo sea. El siguiente es un ejemplo de esta situación.
![]()
![]()
![]()
![Show[{graford[f[x], {x, 0, 14}, PlotRange-> {-.22, 1}], graford[Abs[f[x]], {x, 0, 14}, PlotRange-> {-.22, 1}]}, DisplayFunction→Identity] ;](HTMLFiles/index_525.gif)
![]()
![[Graphics:HTMLFiles/index_527.gif]](HTMLFiles/index_527.gif)
![[Graphics:HTMLFiles/index_528.gif]](HTMLFiles/index_528.gif)
La integral de la función anterior es convergente en [0,+∞[. Puedes pedirle a Mathematica que la calcule.
![]()
![]()
Sin embargo se tiene que 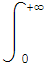 |
|![]() |dx=+∞. Ello es consecuencia de que |
|dx=+∞. Ello es consecuencia de que |![]() |≥
|≥ ![]() |sen x| para k π≤x≤(k+1) π. Por otra parte
|sen x| para k π≤x≤(k+1) π. Por otra parte 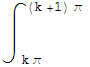 |sen x|dx=
|sen x|dx=![]() |sen x|dx=2. Deducimos que:
|sen x|dx=2. Deducimos que: 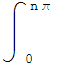 |
|![]() |dx=
|dx=![]() [
[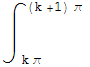 |
|![]() |dx]≥
|dx]≥![]()
![]()
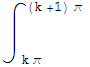 |sen x|dx=
|sen x|dx=![]()
![]()
![]() ≥
≥![]() log n
log n
de donde se deduce que 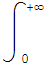 |
|![]() |dx=+∞.
|dx=+∞.
La situación anterior motiva la siguiente definición.
Definición
Se dice que la integral de f es absolutamente convergente en un cierto intervalo cuando la integral de la función | f | es convergente en dicho intervalo.
En otros términos, la integral de f es absolutamente convergente en un intervalo de extremos a, b cuando la región G(f,a,b) tiene área finita.
Naturalmente, los criterios de convergencia antes vistos para integrales de funciones positivas, pueden usarse para estudiar la convergencia absoluta de la integral de cualquier función. Por ello, el siguiente resultado, que no demostraremos, es de gran utilidad.
Teorema
Si la integral de f es absolutamente convergente, entonces la integral de f también es convergente.
Fíjate que la integral de f es absolutamente convergente si. y sólo si, son convergentes las integrales de las funciones ![]() y
y ![]() , en cuyo caso se verifica que
, en cuyo caso se verifica que ![]() f(x)dx=
f(x)dx=![]()
![]() (x)dx-
(x)dx-![]()
![]() (x)dx.
(x)dx.
| Created by Mathematica (September 21, 2008) |