Práctica 3. Resolución de ecuaciones (I)
Muchos problemas de las ciencias y las ingenierías requieren hallar una solución de una ecuación, o equivalentemente, una raíz de una función.
Así pues, dada una función f, nos plantearemos encontrar valores x que hagan f(x)=0. En esta práctica veremos métodos para hallar con Matlab las raíces de una función. En concreto trataremos los métodos de bisección, regula-falsi, secante, los métodos de iteración funcional y el de Newton-Raphson.
Contents
Antes de estudiar estos métodos, veremos dos maneras de definir una función, mediante un archivo .m o como una función anónima y también veremos maneras de representar el eje OX.
Funciones en archivos .m
Pueden definirse funciones en Matlab mediante archivos .m cuya primera linea comienza con function. Una linea como la siguiente serviría para definir una función llamada nombrefuncion con dos argumentos:
function valorsalida=nombrefuncion (argumento1,argumento2)
dentro del código del archivo se debe dar a valorsalida el valor que devuelve la función. Dentro del archivo de la función deben incluirse sólo las instrucciones necesarias para calcular el valor que toma la función, todas las instrucciones que usen la función deben ir fuera del archivo.
Es posible definir una función con varias salidas:
function [salida1 salida2]=nombrefuncion (argumento1,argumento2)
Observe en el siguiente ejemplo una función f.m, que tiene sólo una entrada (la variable x) y sólo una salida (el valor de f). El comando type f.m muestra el contenido del archivo f.m . Tenga en cuenta que la función se usa mediante el nombre del archivo y no mediante el nombrefuncion que se da en la primera linea.
type f.m
function f=f(x) % Ejemplo de función f. % Al emplear .^ la función puede aplicarse a vectores f=1/2-x.^2;
Ej 1. Defina un vector x con valores desde -1 a 1 con paso 0.1. Compruebe que la función f.m puede aplicarse al vector x. (Sol. f(x)=[-0.5, -0.31, -0.14, 0.01, ...] )
Ej 2. Represente la función f en el intervalo [-1,1].
Representación del eje OX
Una forma de representar el eje OX es utilizar, después del comando plot, el comando grid on, que representa una malla o cuadrícula en la gráfica de la función.
x=0:0.1:1;
plot(x,f(x))
grid on
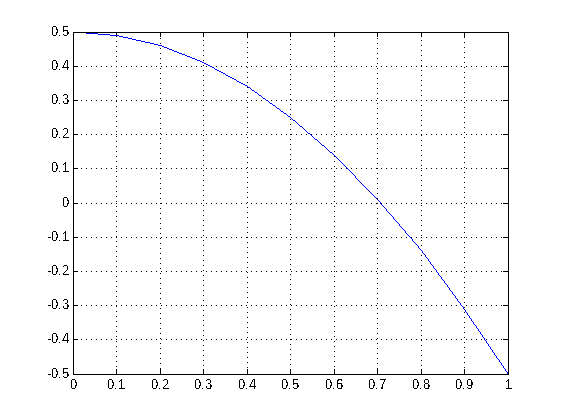
Si en vez de la malla sólo queremos representar el eje OX, podemos dibujar la función y=0.
x=0:0.1:1; y1=f(x); y2=zeros(length(x)); plot(x,y1,x,y2)
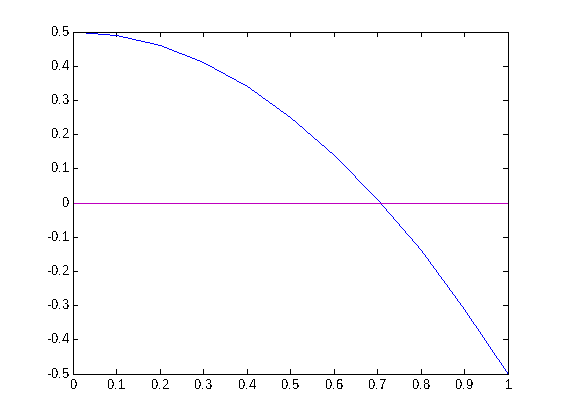
Ej 3. Defina en un script g.m la función g(x)=3/4-1/(1+x^2). Evalúe g(2). Represente la función junto con el eje horizontal en el intervalo [-5,5]. (Sol. 0.55 )
Funciones anónimas
Como vimos, es posible en Matlab definir funciones sin usar archivos .m, por ejemplo la siguiente linea define la función h(x)=x^2+1 .
h=@(x) x.^2+1
h =
@(x)x.^2+1
La sintaxis para definir una función anónima es la siguiente
nombrefuncion=@(argumentos) expresion
Por ejemplo, la siguiente linea define la función n2(a,b)=sqrt(a^2+b^2)
n2=@(a,b) sqrt(a.^2+b.^2)
n2 =
@(a,b)sqrt(a.^2+b.^2)
Ej 4. Sin emplear un archivo .m, defina la función h2(x)=sin(x)^2-cos(x)^2. Halle el valor de h2(0) y de h2(2). (Solución: h2(0)=-1, h2(2)=0.6536)
Localización gráfica de raíces.
En ocasiones podemos usar la gráfica de una función para encontrar un punto cercano a una raíz o encontrar un intervalo que contenga a una raíz.
Ej 5. Defina en un archivo g.m la función g(x)=exp(x)-5x. a) Dibuje la gráfica de g en el intervalo [0,2] junto con el eje OX. b) Represente de nuevo la función en un intervalo más pequeño, de longitud 0.5 que contenga una raiz de g.
Ej 6. Defina de forma anónima las funciones h1(x)=e^(2x) y h2(x)=2-x^2. a) Represente conjuntamente ambas gráficas en el intervalo [-2,1]. b) Represente la función h1(x)-h2(x) en el intervalo [-2,1]. Observe que las raíces de h1(x)-h2(x) son los puntos en los que h1(x)=h2(x), esto es, donde se cortan las gráficas de h1 y h2.
Bisección
Vamos a implementar el método de bisección sin necesidad de almacenar en memoria todas las iteraciones. En esta implementación los extremos del intervalor que contiene la raíz son los valores de a y b. El punto medio del intervalo lo llamaremos c.
Mostramos el pseudocódigo que permite implementar el método de bisección
1. Entrar f , a, b, tol 2. Mientras b-a>=tol 3. Hacer c = a + (1/2)(b-a) 4. Si f (c) = 0 entonces c es raíz. Fin 5. Si sgn f (a) ~= sgn f (c) entonces b = c. 6. Si sgn f (a) = sgn f (c) entonces a = c. 7. Ir a 2
Siguiendo estos pasos se ha implementado el método en el archivo biseccion.m
type biseccion.m
% Método de bisección para una función f definida.
a=0.7;
b=0.8;
tol=0.0001;
while b-a>=tol
% disp([a b]);
c=a+(b-a)/2;
if f(c)==0
break
end
if sign(f(a))~=sign(f(c))
b=c;
else
a=c;
end
end
% disp(c)
En la implementación se ha empleado la instrucción break que interrupe el bucle en que se encuentre, poniendo fin al mismo.
El código escrito tiene algunas limitaciones. Observe que para cambiar los valores iniciales de a y b debe editar el código, y que la función debe llamarse f.
Ej 7. Halle aproximaciones a las dos raíces de la ecuación sin(x)-exp(x^2)+9/10=0. (Sol. aprox. x=0.1132, x=0.6317)
Ej 8. El código del programa contiene dos comentarios que evitan que se muestre el progreso del método y el resultado final. Quite los símbolos de comentario.
Regula-Falsi
El método de regula-falsi es similar al método de bisección, pero los intervalos no se dividen por la mitad. En este método, para cada intervalo se halla la recta que pasa por los puntos de la gráfica en los extremos del intervalo. El punto que divide los intervalos es el corte de la recta hallada con el eje OX. En la implementación almacenamos este punto en la variable c.
Vemos el pseudocódigo del método de regula-falsi
1. Entrar f , a, b, tol 2. Mientras b-a>=tol 3. Hacer c = b - (b-a)*f(b) / (f(b)-f(a)) 4. Si f (c) = 0 entonces c es raíz. Fin 5. Si sgn f (a) ~= sgn f (c) entonces b = c. 6. Si sgn f (a) = sgn f (c) entonces a = c. 7. Ir a 2
Ej 9. Modifique el archivo biseccion.m para implementar el método de regula-falsi en un programa llamado regula.m.
Ej 10. En el código del método de regula - falsi, incluya comentarios que expliquen cada uno de los pasos del método.
Ej 11. Emplee el método de regula - falsi en el intervalo [3,4] para encontrar una aproximación a una raíz de f(x)=cos(x/2). (Sol. aprox. x=3.1416)
Ej 12. ¿Puede emplearse alguno de los métodos vistos hasta ahora para encontrar una raíz de f(x)=exp(x)-5*x en el intervalo [1,2]?
Ej 13. Modifique alguno de los métodos para que el criterio de salida del bucle sea abs(f(c))<tol. (Indicación: defina una variable fin con el valor cero. El bucle debe ejecutarse mientras fin sea cero. Dentro del bucle la variable fin tomará el valor 1 cuando abs(f(c))<tol.)
(Siguiendo esta técnica, pueden implementarse distintos criterios para salir del bucle, e incluso varios criterios en un mismo programa.)
% Ecuaciones Diferenciales y Cálculo Numérico. (A. Palomares) % Grado en Ingeniería de Tecnologías de Telecomunicación. disp(date)
11-Apr-2023