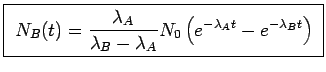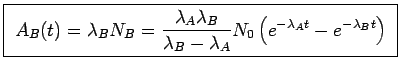

Next: 3.2 Ecuaciones de Bateman
Up: 3 Series radiactivas
Previous: 3 Series radiactivas
Condición inicial:
Núcleo padre:
Núcleo hijo:
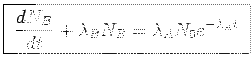
Probamos una solucion:
Queda la ecuación:
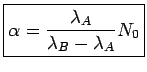
El valor de 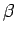 se obtiene imponiendo
se obtiene imponiendo 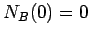 .
.
Solución:
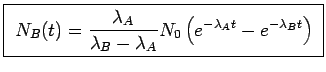
Actividad:
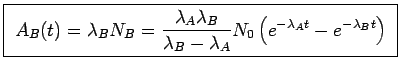


Next: 3.2 Ecuaciones de Bateman
Up: 3 Series radiactivas
Previous: 3 Series radiactivas
J.E. Amaro
2006-05-05
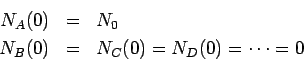
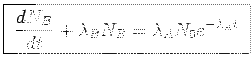
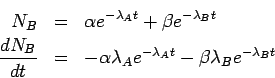
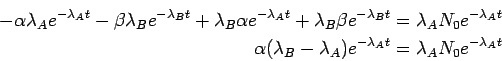
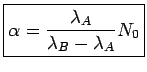
![]() se obtiene imponiendo
se obtiene imponiendo ![]() .
.