


Up: Radiactividad

Problemas Tema 3:
Estructura nuclear y radiactividad
Versión en pdf
- Calcular la energía que debe tener una partícula
 para acercarse
a la superficie de un núcleo de
para acercarse
a la superficie de un núcleo de  Be.
Be.
- El peso atómico del Li es 6.9414, mientras que las masas atómicas de los
únicos isótopos estables,
 Li y
Li y  Li, valen respectivamente
6.015 y 7.016 umas. Obtener la abundancia relativa de ambas especies.
Li, valen respectivamente
6.015 y 7.016 umas. Obtener la abundancia relativa de ambas especies.
- Sabiendo que la masa atómica del
 K es de 39.963999 uma, obtener
la energía de ligadura por nucleón y el exceso de masa en MeV.
K es de 39.963999 uma, obtener
la energía de ligadura por nucleón y el exceso de masa en MeV.
- El exceso de masa del
 P es
P es
 MeV. Calcular
la masa atómica, la energía de ligadura y la energía de ligadura por nucleón.
MeV. Calcular
la masa atómica, la energía de ligadura y la energía de ligadura por nucleón.
- Para la reacción de desintegración
 del
del  Rn, calcular:
(a) la energía liberada, (b) la energía de la partícula
Rn, calcular:
(a) la energía liberada, (b) la energía de la partícula  y (c) la
energía cinética de retroceso del núcleo residual de polonio.
y (c) la
energía cinética de retroceso del núcleo residual de polonio.
- El núcleo de
 U emite una partícula
U emite una partícula  con una energía de
4.20 MeV. ¿Cuál es la energía total liberada en la desintegración?
con una energía de
4.20 MeV. ¿Cuál es la energía total liberada en la desintegración?
- El valor
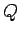 de la desintegración
de la desintegración  del
del  Pu es de 5.25
MeV. Calcular la masa del átomo de
Pu es de 5.25
MeV. Calcular la masa del átomo de  U sabiendo que las masas de los
átomos de
U sabiendo que las masas de los
átomos de  Pu y
Pu y  He son, respectivamente, 239.052171 y 4.002603
uma.
He son, respectivamente, 239.052171 y 4.002603
uma.
- Calcular el valor
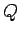 para la desintegración
para la desintegración  del neutrón.
del neutrón.
- Para la desintegración
 del
del  P, calcular (a) la energia
liberada y (b) la energía del anineutrino si el electrón tiene una energía
de 650 keV.
P, calcular (a) la energia
liberada y (b) la energía del anineutrino si el electrón tiene una energía
de 650 keV.
- Calcular el valor
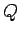 para la desintegración
para la desintegración  del tritio
del tritio
- Dibujar el esquema de desintegración del
 K sabiendo que, por cada
100 desintegraciones, se observan
K sabiendo que, por cada
100 desintegraciones, se observan
18 desintegraciones  con energía máxima del electrón de 1.996
MeV.
con energía máxima del electrón de 1.996
MeV.
82 desintegraciones  con energía máxima del electrón de 3.521
MeV.
con energía máxima del electrón de 3.521
MeV.
18 fotones de 1.525 MeV.
- Una fuente de
 In emite un fotón de 633 keV y un electrón de
conversión interna de 606 keV. Calcular la energía de enlace del electrón.
In emite un fotón de 633 keV y un electrón de
conversión interna de 606 keV. Calcular la energía de enlace del electrón.
- Cierto núclido puede desintegrarse por
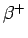 (24%) o captura
electrónica (76%). Las radiaciones de mayor importancia se dan a
continuación, junto con sus energías (en MeV) y porcentajes:
(24%) o captura
electrónica (76%). Las radiaciones de mayor importancia se dan a
continuación, junto con sus energías (en MeV) y porcentajes:
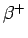 : 1.62 max (16%), 0.98 max (8%)
: 1.62 max (16%), 0.98 max (8%)
 : 1.51 (47%), 0.64 (55%), 0.511 (48%,
: 1.51 (47%), 0.64 (55%), 0.511 (48%, )
)
Rayos X del núcleo hijo
 : 0.614
: 0.614
- Calcular los valores
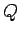 para las desintegraciones
por
para las desintegraciones
por 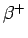 y captura electrónica del
y captura electrónica del  Ni.
Ni.
- Las radiaciones más importantes de cierto núclido son las siguientes
(energías en MeV):
 : 3.92 max (7%), 3.10 max (5%), 1.60 max (88%)
: 3.92 max (7%), 3.10 max (5%), 1.60 max (88%)
 : 2.32 (34%), 1.50 (54%), 0.822 (49%)
: 2.32 (34%), 1.50 (54%), 0.822 (49%)
 : 0.818, 0.805
: 0.818, 0.805
Se pide:
a) dibujar el esquema de desintegración;
b) determinar la máxima energía que puede recibir el antineutrino;
c) calcular el coeficiente de conversión interna;
d) estimar la energía de enlace de los electrones de la capa L del hijo
e) indicar las razones por las que cabe esperar o no, la presencia de rayos X
del hijo
- Considérese la desintegración del
 Cs en
Cs en  Ba. Las energías
de enlace de los electrones de las capas K y L del hijo son de 38 y 6 keV,
respectivamente. Calcular:
Ba. Las energías
de enlace de los electrones de las capas K y L del hijo son de 38 y 6 keV,
respectivamente. Calcular:
a) las energías de los electrones de conversión interna emitidos desde dichas
capas;
b) La longitud de onda de los rayos X de la línea  emitidos por el
bario;
emitidos por el
bario;
c) El coeficiente de conversión interna.
- Calcular el valor
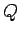 para la captura del electrón orbital
para la captura del electrón orbital  por el
núcleo
por el
núcleo  Ar,
Ar,
a) despreciando la energía de enlace del electrón y
b) incluyendo dicha energía, que es de 3.20 keV
- ¿Cuál es la máxima energía posible para el positrón en la
desintegración del
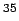 Ar?
Ar?
- Demostrar que el
 Fe puede desintegrarse mediante captura
electrónica, pero no mediante
Fe puede desintegrarse mediante captura
electrónica, pero no mediante 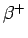



Up: Radiactividad
J.E. Amaro
2006-03-16


con energía máxima del electrón de 1.996 MeV.
con energía máxima del electrón de 3.521 MeV.
: 1.62 max (16%), 0.98 max (8%)
: 1.51 (47%), 0.64 (55%), 0.511 (48%,
)
: 0.614
: 3.92 max (7%), 3.10 max (5%), 1.60 max (88%)
: 2.32 (34%), 1.50 (54%), 0.822 (49%)
: 0.818, 0.805
emitidos por el bario;