Propiedades de las Rocas de Construcción y Ornamentación
Las rocas, y otros materiales pétreos artificiales utilizados en la construcción, son sustancias heterogéneas caracterizadas por amplios rangos de variación composicional, textural y estructural. Esta variabilidad hace que las propiedades de los materiales, que son las que dictan sus campos de aplicación, sean también variables. Así, la adecuación de un material para un propósito concreto, tanto desde el punto de vista constructivo-ornamental como restaurador, debe basarse en determinadas propiedades que deben, a su vez, ser fácilmente medibles en el laboratorio.
Las propiedades de los materiales se clasifican generalmente como físicas, químicas y mecánicas, aunque en el campo de la construcción/ornamentación/restauración también pueden incluirse las propiedades relacionadas con su trabajabilidad. Es evidente que la lista de propiedades que pueden medirse en un material es muy extensa. Por ello en este tema se presentan aquellas que tienen más relevancia desde el punto de vista que nos atañe.
Dentro de las propiedades físicas se incluyen densidad, porosidad, permeabilidad a líquidos y gases, capacidad calorífica, conductividad y expansión térmicas, etc. Entre las propiedades químicas pueden incluirse la resistencia a soluciones ácidas y alcalinas, y a las reacciones inducidas por la presencia de sales. Las propiedades mecánicas incluyen la resistencia a la compresión, tensión, flexión e impacto y penetración por otro cuerpo y por otras acciones que involucran la generación de fuerzas, como la cristalización de hielo y sales en el interior del sistema poroso de los materiales y los cambios volumétricos de los mismos debidos a cambios de temperatura.
Estas propiedades, que en última instancia resultan de la composición química y mineralógica de los materiales, de su textura y de su estructura, permiten caracterizar la resistencia de los materiales a los agentes de deterioro. Esto último gobierna la vida útil del material, que a fin de cuentas es equivalente a la vida útil de las partes del edificio construidas con el mismo y, para determinados elementos constructivos, del edificio mismo.
Una misma propiedad de un material puede
medirse en distintos aparatos, bajo distintas condiciones experimentales y
utilizando probetas de muestra de distintas dimensiones y formas. Esto supone
generalmente obtener resultados distintos para una misma propiedad, por lo que
éstas deben medirse siguiendo normativas que aseguren que los datos obtenidos
son comparables con los obtenidos en otros laboratorios. Entre estas normas
cabe mencionar las de
1.Propiedades Fisicas
1.1.Isotropía y anisotropía
Estos conceptos se utilizan para calificar el comportamiento de los materiales respecto de las direcciones del espacio. Así, un material es isótropo respecto de una propiedad determinada cuando esa propiedad no varia al variar la dirección en la que se mida la propiedad. En este caso, se dice que la propiedad es escalar. Por el contrario, un material es anisótropo cuando la propiedad varía según la dirección considerada. En este caso, la propiedad es vectorial.
1.2.Densidad y peso especifico (ASTM #12-70)
Tanto la densidad como el peso específico son propiedades que no dependen de la dirección de medida, esto es, son propiedades escalares
Aunque se utilizan indistintamente, los
términos de densidad y peso específico no son idénticos. La densidad
es la relación entre la masa y el volumen de la sustancia, midiéndose
en unidades de masa/unidades de volumen (e.g., g/cc). El peso específico es la relación
numérica entre el peso de un cuerpo y el peso de igual volumen de agua a
Densidad = masa/volumen (gr/cc)
Peso específico = Densidad cuerpo/Densidad agua a
En los minerales, ambas magnitudes son función de la estructura cristalina y la composición del mineral, así como de la temperatura y presión, ya que los cambios de estos factores provocan contracciones (descenso de T y/o aumentos de P) o expansiones (aumento de T y/o descenso de P) de las estructuras. Los cambios de estructura afectan a estas magnitudes; así por ejemplo, la calcita presenta un peso específico de 2.72 y el aragonito 2.94, y el cuarzo-a 2.65 y el cuarzo-b 2.40. La composición también afecta en el caso de los minerales solución sólida; así por ejemplo, el peso específico del olivino aumenta a medida que los átomos de Fe (más pesados) sustituyen a los de Mg (más ligeros), pasando de 3.22 para el Mg2[SiO4] (forsterita pura) a 4.41 para el Fe2[SiO4] (fayalita pura).
Cuando se consideran otro tipo de sustancias (por ejemplo, rocas), la densidad o densidad real se define como la masa por unidad de volumen de una sustancia, esto es la razón entre la masa en reposo y su volumen, considerando sólo la parte impermeable (esto es, excluyendo el volumen ocupado por los poros):
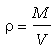
donde: r es la densidad (kg/m3)
M es la masa (kg) de la sustancia y
V es el volumen (m3) de la parte impermeable de la sustancia.
La densidad de algunos materiales de
construcción se presenta en
|
Tabla 1. Densidad (kg/m3) de algunos materiales de construcción (de Komar, 1987). Acero 7800-7900 Cemento Portland 2900-3100 Granito 2700-2800 Arena cuarzosa 2600-2700 Ladrillo 2500-2800 Vidrio 2500-3000 Caliza 2400-2600 Madera 1500-1600 |
La densidad global (a veces también denominada densidad aparente) es la masa por unidad de volumen de un material en su estado natural, incluyendo poros y todo tipo de espacios abiertos:

donde: ro es la densidad global del material (kg/m3)
M1 es la masa global (kg) del material y
V1 es el volumen global (m3) del material.
La densidad global de los materiales depende de su porosidad y contenido de espacios abiertos. Materiales sueltos como arena, piedra molida y cementos se caracterizan por su masa global. El volumen de estos materiales incluye tanto los poros y espacios abiertos existentes dentro de los granos como entre los granos. La densidad global de los materiales condiciona en gran medida sus propiedades fisico-mecánicas, tales como resistencia a la compresión y conductividad térmica, que a su vez son cruciales para cálculo de estructuras y diseño de edificios. Evidentemente, la densidad global de los materiales es fuertemente variable (Tabla 2).
El peso específico o peso específico verdadero de una sustancia es la razón entre la masa de una unidad de volumen de la sustancia y la masa de la misma unidad de volumen de agua destilada. Para los sólidos, el volumen considerado es el de la parte impermeable. El peso específico global se define de manera similar, aunque considera el volumen total del cuerpo, incluyendo los poros.
|
Tabla 2. Densidad global (kg/m3) y porosidad (%) de rocas y materiales de construcción (de Winkler, 1973 y Komar, 1987) Densidad global Porosidad Acero 7800-7850 Granito 2600-2800 0.15-1.5 Gabro 3000-3100 0.1-0.2 Riolita 2400-2600 4.0-6.0 Basalto 2800-2900 0.1-1.0 Arenisca 2000-2600 5.0-25.0 Lutita 2000-2400 10.0-30.0 Caliza 2200-2600 5.0-20.0 Dolomia 2500-2600 1.0-5.0 Gneiss 2900-3000 0.5-1.5 Mármol 2600-2700 0.5-2.0 Cuarcita 2650 0.1-0.5 Pizarra 2600-2700 0.1-0.5 Hormigón pesado 1800-2500 Hormigón ligero 500-1800 Ladrillo 1600-1800 Arena 1450-1650 Plástico poroso 20-100 |
1.3.Porosidad
La porosidad de un material es el volumen de espacios abiertos que contiene relativo a su volumen total. Los poros son pequeños espacios abiertos existentes en los materiales rellenos por soluciones acuosas y/o gaseosas (e.g., aire). Los poros pueden estar abiertos (i.e., intercomunicados) o cerrados, y ser grandes o pequeños. El tamaño de poro medio y el grado de intercomunicación entre los poros determinan el tipo y grado de movimiento de soluciones líquidas y gaseosas por el interior de los materiales. Esto controla en gran parte su durabilidad. Los poros pueden clasificarse en función de su tamaño en:
Ø Megaporos:_____________ 256-
Ø Macrocapilares:_________ 0.062-
Ø Microcapilares:_________ <
Existen distintos conceptos de porosidad. La porosidad teórica viene dada por la ecuación:
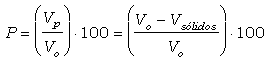
donde: P es la porosidad total (%)
Vp (m3) es el volumen de poros
Vsólidos (m3) es el volumen agregado de las partículas sólidas y
Vo (m3) es el volumen total de la muestra.
Teniendo en cuenta que la relación entre masa, volumen y densidad, y que la masa del material poroso es idéntica a la masa de la sustancia (sin poros) si los poros están ocupados por vacío, la expresión anterior queda:
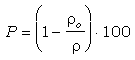
donde: P es la porosidad total (%)
ro es la densidad global del material (kg/m3) y
r es la densidad real de la sustancia (kg/m3), asumiéndola libre de poros.
La densidad de la sustancia libre de poros es difícil de estimar. Por ello se recurre a otro tipo de mediciones. La porosidad total efectiva es la porosidad medible mediante intrusión de mercurio hasta una presión forzada de 1000 atmósferas, aunque se puede llegar hasta varios miles de atmósferas:
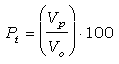
donde: Pt es la porosidad total efectiva (%)
Vp (m3) es el volumen de mercurio intuido y
Vo (m3) es el volumen de la muestra seca.
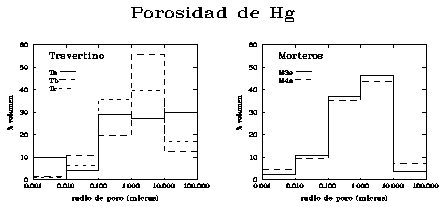
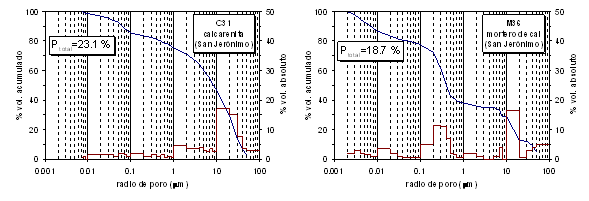
Mediante la técnica de intrusión forzada de
mercurio puede estimarse no sólo la porosidad total efectiva, sino la porosidad
media (%) comprendida entre un determinado rango de tamaño de poro,
medido en términos de radio o diámetro de poro. En general, los aparatos (porosímetros de Hg) más comunes
permiten evaluar los porcentajes de radios de poro menores de
Otra medida de la porosidad se puede obtener mediante pesada hidrostática, que define la porosidad abierta o accesible al agua. El material se sumerge en agua (u otro líquido de densidad conocida) hasta su saturación (ver más adelante), calculándose la porosidad a partir de la masa del material seco, saturado y saturado por pesada hidrostática (i.e., peso de la muestra saturada inmersa en un recipiente con agua) mediante la expresión:
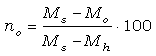
donde: no es la porosidad abierta (%)
Ms (kg) es el peso medido en saturación
Mo (kg) es el peso seco de la muestra, y
Mh (kg) es el peso de la muestra saturada medida por pesada hidrostática.
Al contrario que la porosidad total efectiva medida por intrusión forzada, la porosidad abierta da información sobre la porosidad debida a los poros más gruesos por los que el agua puede circular. No obstante, no se pueden extraer valores de porosidad media para distintos rangos de tamaño de poro. Las dimensiones de las probetas de muestra son las mismas que las utilizadas para estimar la saturación de agua.

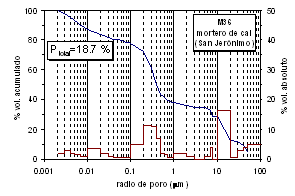
Figura 1. Porosidad total por intrusión de Hg y distribución de la porosidad en función del radio de poro (% volumen absoluto y acumulado) en biocalcarenita y mortero de cal de San Jerónimo, Granada (de Fernández-Cardell, 1998).
1.4.adsorcion y Absorcion de Agua
Estas propiedades se relacionan con la movilidad de vapor de agua o agua líquida en los materiales, esto es con la permeabilidad del medio a estas sustancias:
· Adsorción es la adhesión de moléculas de gases o de moléculas en solución a las superficies de los cuerpos sólidos con los que están en contacto. La higroscopicidad es la propiedad de los materiales de adsorber vapor de agua de la atmósfera.
· Absorción es la incorporación o asimilación de líquidos en el interior del sistema poroso del material. La succión de agua es la propiedad de los materiales de absorber agua líquida en contacto con los mismos.
La higroscopicidad está controlada por la temperatura y humedad relativa del aire, por los tipos de poros, su número y tamaño, y por la naturaleza de la sustancia implicada. Debido a la naturaleza polar del agua, este último control se debe a la existencia o no de cargas residuales no compensadas en las superficies de las sustancias. Así, las superficies de algunas sustancias compuestas por átomos con enlaces iónicos atraen al agua (i.e., sustancias hidrófilas) mientras que las superficies de otros compuestos por átomos con enlaces covalentes la repelen (i.e., sustancias hidrófobas). Las sustancias hidrófilas tienen a disolverse en agua, mientras que las hidrófobas no, resistiendo la acción de los medios acuosos.
A igualdad de otros factores, la higroscopicidad de un material depende del área superficial expuesta, i.e., incluyendo la de los poros y canales capilares. Los materiales con idéntica porosidad total, pero con poros más finos (capilares) son más higroscópicos que los que presentan poros grandes, lo cual es debido a que los primeros presentan mayor superficie específica.
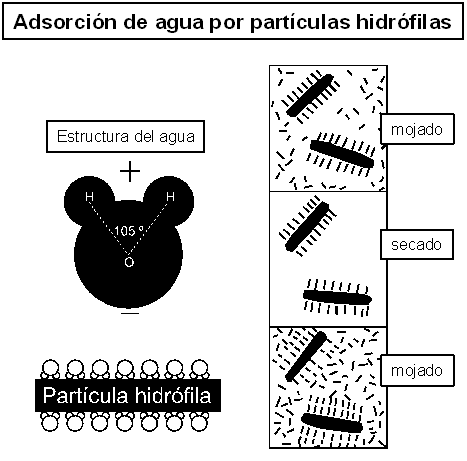
Figura 2. Adsorción de moléculas agua (polares) por partículas hidrófilas (con cargas electrostáticas residuales en su superficie) durante ciclos de mojado y secado.
La succión de agua en el interior de los sistemas porosos de los materiales incluye también la higroscopicidad. La saturación en agua afecta de forma sustancial a otras propiedades físicas y mecánicas de los materiales, tales como densidad global, conductividad térmica y resistencia mecánica, por lo que su medida es importante. La técnica es muy sencilla, y se basa en sumergir una probeta de muestra completamente en agua, a tiempos parciales, y medir el incremento de masa de las probetas en esos tiempos. Las recomendaciones del Documento NORMAL 7/81 indican utilizar probetas cúbicas de 5x5x5 cm. Los incrementos de masa permiten calcular la cantidad de agua absorbida:
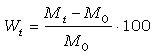
donde: Wt (%) es el contenido de agua absorbida en el tiempo t (s)
Mt (kg) es el peso medido en el tiempo t (s) y
Mo (kg) es el peso seco de la muestra
Por lo tanto, Wt representa incrementos de masa en % relativos al material seco.
Estos datos permiten construir curvas Wt-t (generalmente, el tiempo se expresa como ![]() ),
que caracterizan el comportamiento del material.
),
que caracterizan el comportamiento del material.
La absorción de agua es función de la porosidad total, y del tamaño y forma de los poros. Así, la cantidad de agua absorbida es siempre menor que la porosidad total del material ya que parte de los poros se encuentran cerrados, i.e., aislados del medio exterior y no accesibles al agua. Dado que los porcentajes de agua absorbida son proporcionales a la porosidad del material, y esta puede variar entre distintos materiales, se recurre a una normalización ulterior para comparar materiales de porosidad variada. Esta normalización se lleva a cabo respecto del porcentaje en peso de agua bajo saturación forzada, esto es, bajo condiciones de presión mucho menores de la atmosférica, tendiendo al vacío, recalculando el incremento de masa en los distintos tiempos respecto de la cantidad máxima de agua absorbida (Wt,max), esto es, el porcentaje de peso de agua para el tiempo t. Esta normalización permite obtener el grado de saturación en función del tiempo:
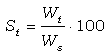
donde: St es el grado de saturación (%)
Wt (%) es el porcentaje de peso de agua en el tiempo t (s) y
Ws (%) es el porcentaje en peso de agua bajo la saturación forzada.
1.5.Desorcion de Agua
Los materiales localizados en contacto con el aire retienen cierta cantidad de humedad. La cantidad de agua retenida es función de las condiciones ambientas (temperatura y humedad relativa), así como de la naturaleza de las sustancias (hidrófilas o hidrófobas) y de la composición de la solución acuosa (agua pura vs. soluciones salinas). Si las condiciones ambientales cambian, por ejemplo, descendiendo la humedad relativa, el material tiende a ceder vapor de agua al medio aéreo, secándose. Este proceso de desorción de agua es inverso al de adsorción, aunque si la muestra se encuentra saturada en agua, es inverso al de absorción.
La tasa de desorción o secado depende de la diferencia entre la humedad del material y la del medio ambiente (a mayor diferencia, mayor tasa de secado), de la naturaleza del material y de la naturaleza de la porosidad (sustancias hidrorepelentes con poros grandes tienden a eliminar más rápidamente la humedad).
La técnica de medición de la desorción de agua es similar a la de saturación de agua, y
persigue evaluar la facilidad de los materiales para eliminar el agua absorbida
en el interior de su sistema poroso. El ensayo se realiza con el mismo material
utilizado en el de saturación, y se basa en medir las pérdidas de masa, a
tiempos parciales, respecto del peso de la muestra saturada en agua. Este
ensayo debe realizarse en un ambiente con temperatura (
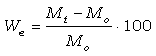
donde: We (%) es la cantidad de agua perdida
Mt (kg) es la masa medida en el tiempo t (s) y
Mo (kg) es el peso de la muestra saturada en agua.
Por lo tanto, We representa pérdidas
de masa en % relativos al material saturado. Igualmente, estos datos permiten
construir curvas We-t
(generalmente, el tiempo se expresa como ![]() ),
que caracterizan el comportamiento del material.
),
que caracterizan el comportamiento del material.
Al igual que en el caso de absorción, se calcula el grado de saturación en función del tiempo con el fin de comparar muestras de porosidad muy variada:
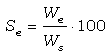
donde: Se (%) es el grado de saturación
We es el porcentaje de peso de agua en el tiempo t (seg) y
Ws es el porcentaje en peso de agua bajo la saturación forzada.
Las tasas de saturación observadas en los ensayos de absorción y desorción, evaluadas mediante las curvas respectivas St-t y Se-t no tienen porque coincidir. Esto se debe a que los procesos físicos involucrados en ambos procesos son distintos.
Como se ha indicado más arriba, la humedad en los materiales de construcción afecta a sus propiedades físicas y mecánicas. El principal efecto es un cambio de volumen: los materiales se hinchan cuando absorben agua y se contraen al evacuarla. Dado que los cambios de volumen generan tensiones internas en los materiales, ciclos continuados a escala diaria y estacional de mojado-secado inducen esfuerzos alternantes en el material que, aunque poco significativos en términos absolutos para materiales pétreos, generan pérdida de resistencia mecánica por fatiga (ver más adelante). Un ejemplo claro son los morteros, cuyo aglomerante (cal, cemento) sufre contracción durante el secado mientras el árido no, lo que genera esfuerzos tensionales que conllevan la pérdida de cohesión del agregado por microfracturación del aglomerante. Ensayos de ciclos de secado-mojado durante largos periodos de tiempo permiten calificar la resistencia al deterioro por esta causa.
1.6.Capilaridad
El fenómeno de la capilaridad, cuyo resultado es el movimiento ascendente o descendente de un líquido en el interior de un tubo fino de un material sólido cuando éste es sumergido en el líquido, es debido a la existencias de fuerzas en la superficie de las sustancias sólida (e.g., vidrio), líquida (e.g., agua) y gaseosa (e.g., aire) en contacto. Estas fuerzas se denominan de tensión superficial. La conjunción de estas fuerzas hace que las gotas de un líquido depositadas sobre la superficie de un material sólido presenten ángulos de contacto sólido-líquido variados en función de la naturaleza de los sólidos y líquidos. Así, los líquidos “mojan” a los sólidos cuando el ángulo de contacto está comprendido entre 0 y 90º, en cuyo caso el líquido asciende por el capilar. Si por el contrario la conjunción de fuerzas mencionada anteriormente condicionan que el ángulo de contacto sólido-líquido esté comprendido entre 90 y 180, el líquido no moja al material y desciende por el capilar. Estas relaciones se ilustran en las Figuras 3 y 4. En consecuencia, el efecto que debe producir un material hidrofugante (protectivo o consolidante) aplicado sobre un material debe ser el de incrementar el ángulo de contacto del material pétreo, y obstaculizar el ascenso del agua por su sistema poroso. El efecto contrario es el obtenido por los agentes detergentes o jabones (i.e., tensoactivos).
La altura a la que asciende (o desciende) un líquido en un capilar no es sólo función del ángulo de contacto, sino que depende también del radio del capilar. La ecuación que permite calcular la altura alcanzada es:
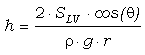
![]()
donde: h es la altura (m)
SLV es la tensión superficial
líquido-vapor (0.0728 N/m para el agua-aire, a
q es el ángulo de contacto (en radianes, = grados·p/180)
r es la densidad del líquido (1000 kg/m3
para el caso del agua)
g es la aceleración de la gravedad (9.8 m/seg2) y
r es el radio de poro (m)
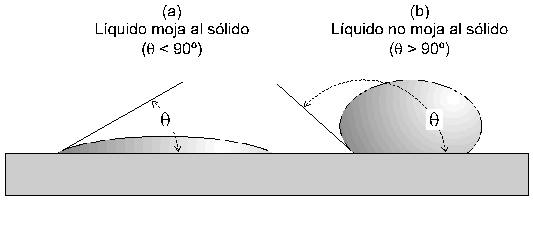
Figura 3. Variación en el ángulo de contacto sólido-líquido. En (a) el líquido (e.g., agua) moja al sólido (e.g., piedra), y q < 90º, mientras que en (b) el líquido (e.g., mercurio) no moja al sólido y q > 90º.
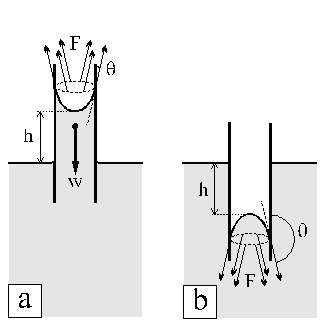
Figura 4. Fuerzas resultantes (F) de la conjunción de las tensiones superficiales en un sistema sólido-líquido-gas en un tubo capilar (w es el peso de la columna de agua para el caso a). El líquido se eleva una altura h si (a) q < 90º, y desciende si (b) q > 90º.
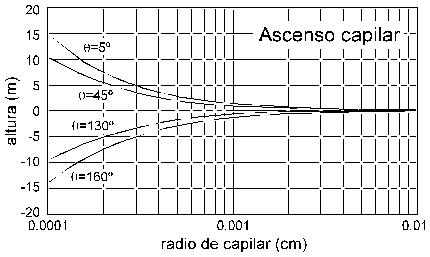
Figura 5. Curvas altura-radio de capilar calculadas para el sistema agua-aire.
La rutina de trabajo (recomendaciones RILEM y NORMAL 11/85) consiste en la colocación de las probetas (la relación de área/volumen de la probeta cúbica, prismática o cilíndrica debe estar comprendida entre 1 y 2 cm-1) sobre una superficie mojada, dentro de una cubeta de material plástico con agua destilada e interfase de papel absorbente para asegurar un flujo de humedad continua, sin llegar a mojar otra superficie que no sea la base de la probeta. Para evitar una rápida evaporación del agua de la cubeta, ésta se cubre con una tapadera de plástico protegida con papel absorbente para evitar el goteo de condensación sobre las probetas junto con las paredes laterales de la cubeta. El recipiente debe colocarse dentro de una campana aislante con unos valores de temperatura y de humedad relativa constantes.
El ensayo consiste en pesar y medir la altura del agua sobre las diferentes probetas a tiempos parciales. Las pesadas se realizan eliminando previamente el exceso de agua depositada sobre la base de las probetas con una bayeta absorbente ligeramente humedecida; de esta forma se retiran los excesos de agua sin llegar a restar parte de la contenida en la probeta. Los resultados que se obtienen con el ensayo son los siguientes: peso en función del tiempo (Mt) expresado en gramos y altura ascendida en función del tiempo (ht) expresada en centímetros. La cantidad o incremento de agua absorbida de la muestra, por unidad de superficie en el tiempo se calcula con la siguiente ecuación:
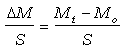
donde: M/S es el incremento de masa por unidad de superficie (kg/m2)
Mt (kg) es el peso de la muestra en función del tiempo t (s)
M0 (kg) es el peso de la muestra seca y
S es el área (m2) de la cara de la probeta en contacto
con el agua.
Con los datos obtenidos es posible construir
dos curvas, una de absorción capilar y otra de ascenso capilar, en función de ![]() (min0.5). La primera se traza en
función del incremento de peso experimentado por la probeta a lo largo del
ensayo, la segunda curva representa la altura de agua ascendida en función del
tiempo transcurrido. Además de observar el comportamiento del material, se
pueden obtener el coeficiente de absorción capilar (con dimensiones kg/m2·s0.5)
y el coeficiente
de penetración capilar (con dimensiones m/s0.5) obtenidos
mediante cálculos de regresión en los tramo rectilíneos de las curvas.
(min0.5). La primera se traza en
función del incremento de peso experimentado por la probeta a lo largo del
ensayo, la segunda curva representa la altura de agua ascendida en función del
tiempo transcurrido. Además de observar el comportamiento del material, se
pueden obtener el coeficiente de absorción capilar (con dimensiones kg/m2·s0.5)
y el coeficiente
de penetración capilar (con dimensiones m/s0.5) obtenidos
mediante cálculos de regresión en los tramo rectilíneos de las curvas.
2.Propiedades Mecanicas
Las propiedades mecánicas definen la capacidad del material para resistir acciones externas o internas que implican la aplicación de fuerzas sobre el mismo. Esencialmente, estas fuerzas son de compresión, tensión (o extensión), flexión y de impacto.
2.1.Resistencia
a la Compresion
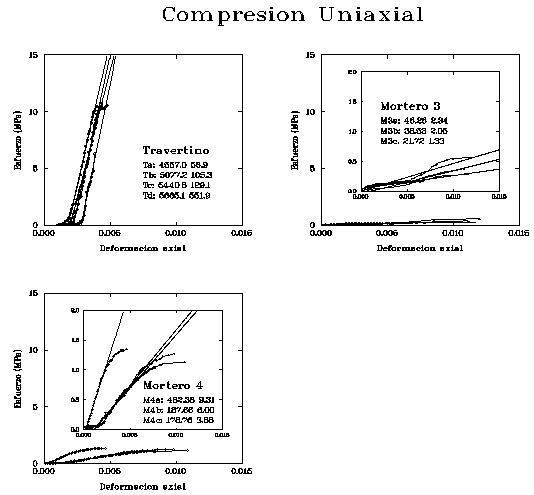
La resistencia a la compresión es la carga (o peso) por unidad de área a la que el material falla (se rompe) por fracturación por cizalla o extensional (Figura 6). Esta propiedad es muy importante en la mecánica de materiales, tanto en situación no confinada (i.e., uniaxial) como confinada (i.e., triaxial). Dado que los materiales cerca de la superficie terrestre, incluyendo los edificios, suelen estar sometidos a condiciones no confinadas, consideraremos exclusivamente esta situación. En este caso, la resistencia a la compresión uniaxial (i.e., longitudinal) se mide en una prensa hidráulica que registra el esfuerzo compresor (sl) aplicado sobre una probeta de material en una dirección del espacio, y la deformación lineal (el) inducida en esa misma dirección.
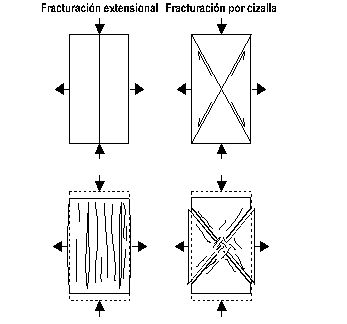
Figura 6. Desarrollo de fracturas extensionales y de cizalla como resultado de compresión.
Es importante indicar que los resultados
obtenidos en los experimentos de resistencia a la compresión para un mismo
material depende de la forma y tamaño de la probeta. Así, los prismas y
cilindros largos presentan menores resistencias a la compresión que los cubos
con la misma área de sección, y estos a
su vez menores que los prismas y cilindros cortos (con alturas menores que sus
lados o radios). Igualmente, la resistencia a la compresión depende de la tasa
de aplicación de la carga, de forma que a mayores velocidades de compresión
mayor es el valor de la resistencia. La metodología experimental puede seguir
la norma ASTM D3148-86, según la cual las probetas de muestra serán
cilíndricas, con una relación altura/diámetro comprendida entre 2.5 y 3 (e.g.,
El esfuerzo es igual a la fuerza aplicada por sección o superficie:
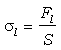
donde: Fl es la fuerza aplicada longitudinalmente, expresada en newtons en el sistema mks (N=kg·m·s-2), dinas en el sistema cgs o kilogramos-fuerza en el sistema técnico
S es la sección de la probeta (m2) y
sl es el esfuerzo lineal expresado en Pa (N/m2), dinas/cm2 o kg/m2 (las dimensiones del esfuerzo son las mismas que las de presión).
Dado que la fuerza es un vector, también lo es el esfuerzo. Así, dado que el signo de la fuerza se toma negativo por convenio cuando es compresiva, y positivo cuando es tensional, el esfuerzo compresor es negativo y el tensor es positivo.
La deformación lineal es igual al cambio de longitud experimentado por la longitud original de la probeta:
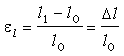
donde: l0 (m) es la longitud original
l1 (m) es la longitud final
Dl (m) es el incremento de longitud de la probeta.
Puesto que al comprimir l0 es siempre mayor que l1, l y l son negativos (positivos para el caso de tensión). El valor de el (que es adimensional) es generalmente muy pequeño para materiales pétreos (del orden de 0.01 y menores).
La deformación inducida sobre un cuerpo debida a la acción de un campo de fuerzas exteriores puede ser elástica o plástica. La deformación es elástica cuando el cuerpo recupera su forma y volumen iniciales una vez cesada la acción de las fuerzas externas. En caso contrario, la deformación es plástica (esto es, si la deformación persiste en parte). El que la deformación sea elástica o plástica depende de la naturaleza del cuerpo, de la temperatura, y del grado y tasa (velocidad) de deformación al que ha sido sometido. A temperatura constante, los materiales se comportan normalmente como elásticos cuando los esfuerzos aplicados son pequeños, si bien se tornan plásticos cuando los esfuerzos superan un cierto límite.
Para estudiar el comportamiento mecánico de
los materiales, se recurre a la experimentación sometiendo a los mismos a
esfuerzos progresivos y registrando la deformación resultante. Estos datos se
expresan en diagramas sl-el como los de
![]()
donde el módulo de elasticidad E es positivo (sl y el son negativos) y presenta las mismas dimensiones que el esfuerzo ya que el es adimensional. El valor del módulo de Young es característico para distintos materiales, por lo que puede utilizarse para comparar las características mecánicas de los mismos.
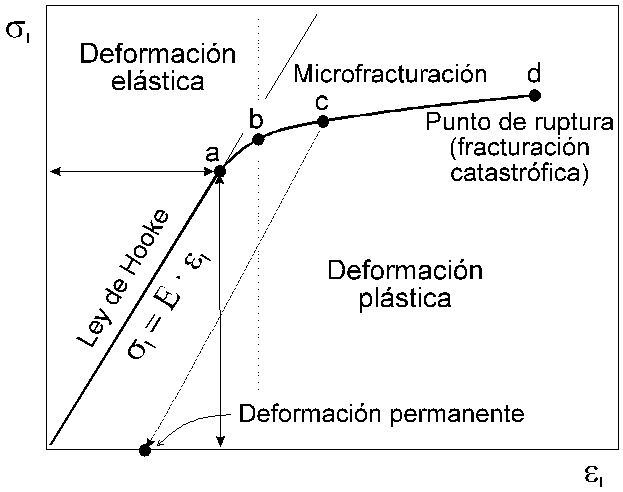
Figura 7. Curva esfuerzo-deformación para compresión, con ilustración de los tramos elástico y plástico.
Para deformaciones superiores al límite de
proporcionalidad, existe un cierto tramo de la curva sl-el donde el
comportamiento del material es elástico, aunque no existe proporcionalidad
entre el esfuerzo y la deformación. El límite en el que el comportamiento del
material deja de ser elástico se denomina límite elástico, representado por el
punto b de la curva en
Al aumentar el esfuerzo y superarse el límite elástico (punto b), la deformación aumenta rápidamente y es en parte permanente. Así, si se disminuye el esfuerzo aplicado lentamente a partir del punto c de la curva, se recorrerá el trayecto indicado por una flecha de puntos hasta alcanzar el punto donde el esfuerzo es nulo, pero existe una cierta deformación permanente (el cuerpo no recupera su longitud original). Al aumentar el esfuerzo se llega finalmente al punto d, denominado punto de ruptura, donde el cuerpo experimenta una fracturación catastrófica por cizalla o fisuración extensional. Este punto de ruptura define, en términos del esfuerzo compresivo, la resistencia a la compresión (R).
La resistencia a la compresión de los materiales de construcción es muy variable, oscilando desde materiales:
· muy débiles (<70 kg/cm2)
· débiles (70-200 kg/cm2)
· moderadamente resistentes (200-700 kg/cm2)
· fuertes (700-1400 kg/cm2) hasta
· muy fuertes (>1400 kg/cm2).
Las rocas naturales son relativamente resistentes a la compresión (no tanto a la tensión y flexión), aunque las rocas sedimentarias son las más débiles debido sobre todo a su mayor porosidad y variable grado de cementación, al igual que los hormigones (Tabla 3). Aunque no puede generalizarse el efecto del tamaño de grano, puede decirse que, en general, la resistencia a la compresión aumenta a medida que aumenta el tamaño de grano de los materiales, a igualdad de otras variables como composición mineral, estructura, porosidad, cementación, etc.
|
Tabla 3. Resistencia a la compresión de algunas rocas y materiales de construcción (modificado de Winkler, 1973). (Mpa) kg/m2·106 kg/cm2·103 Granito 97 310 10 32 1.0 3.2 Sienita 186 434 19 44 1.9 4.4 Gabro, diabasa 124 303 13 31 1.3 3.1 Basalto 110 338 11 34 1.1 3.4 Caliza 14 255 1 26 0.1 2.6 Arenisca 34 248 4 25 0.4 2.5 Gneiss 152 248 15 25 1.5 2.5 Cuarcita 207 627 21 64 2.1 6.4 Mármol 69 241 7 25 0.7 2.5 Pizarra 138 207 14 21 1.4 2.1 Hormigón 5.5 69 1 7 0.1 0.7 |
La resitencia a la compresión de rocas utilizada en monumentos granadinos son (valores obtenidos en seco por Guardia Olmedo et al., 1986, Arte y Deterioro en los Monumentos Granadinos. Catedral, Chancillería y Palacio de Carlos V. Universidad de Granada, 140 p.)
|
Tabla 4. Resistencia a la compresión de rocas utilizadas en monumentos granadinos (Guardia Olmedo et al., (1986). Calcarenita: 75-500 kg/cm2 Travertino: 400-700 kg/cm2 Conglomerados: 200 kg/cm2 Caliza de Sierra Elvira: 600-900 kg/cm2 Mármol de Macael: 680-980 kg/cm2 Serpentinita: 400-700 kg/cm2 |
Las relaciones
entre esfuerzo y deformación ilustradas en
Por otro lado, los materiales pueden clasificarse como frágiles y dúctiles (Figura 9). Los materiales frágiles (como el vidrio) se rompen cuando se supera el límite elástico, (b y d son muy cercanos), mientras que los materiales dúctiles (como el acero o el cobre) presentan un tramo de comportamiento plástico amplio.
Los materiales pétreos pueden caracterizarse, en general, como frágiles bajo condiciones de temperatura ambiental (si bien a altas presiones y temperaturas presentan tramos plásticos más amplios, Figura 9). La deformación permanente entre el límite elástico y el punto de ruptura en los materiales heterogéneos como los pétreos se verifica a bajas temperaturas mediante una microfracturación frágil. Esta microfracturación se produce sobre todo en el interior de los minerales que forman las rocas, a favor de sus sistema de exfoliación, o entre microporos. El grado de microfracturación, que es controlado por las características texturales y estructurales de los materiales (e.g., tamaño de grano, porosidad, razón clastos/matriz, cementación, etc.), define en gran medida la forma de la curva esfuerzo-deformación. Así, puede generalizarse que los materiales pétreos con tamaño de grano fino tienden a ser casi-elásticos, mientras que los de grano grueso tienden a ser semi-elásticos, siempre a igualdad de otros factores. Respecto de la porosidad, materiales compactos y poco porosos tenderán a un comportamiento casi-elástico o semi-elástico, mientras los materiales muy porosos y poco o moderadamente coherentes (esto es, escasamente cementados, como las calcarenitas bioclásticas utilizadas en la construcción de edificios históricos de Granada o morteros de cal) tienden a un comportamiento semi-elástico o plástico. El comportamiento semi-elastico o plástico indica un rápido aumento de la deformación en los primeros incrementos de esfuerzo, lo cual se explica por acomodo de la carga por el movimiento relativo de los granos (gruesos) del entramado y/o deformación de los poros, pasándose a continuación a una situación en que la tasa de deformación es menor, esto es, de recuperación mecánica, en la que el esfuerzo y la deformación aumentan más o menos proporcionalmente una vez el entramado de granos ha adquirido cierta compactación (Figura 8).
Como puede deducirse de lo anterior, el módulo de Young sólo puede definirse en rigor cuando los materiales elásticos, ya que la proporcionalidad lineal entre esfuerzo y deformación no se verifica en los materiales casi-elásticos, semi-elásticos y plásticos. A pesar de ello, este módulo puede calcularse para partes determinadas de las curvas esfuerzo-deformación, aunque sin el conocimiento de sus formas este dato sirve de poco. No obstante, cuando los materiales son frágiles, y su comportamiento es elástico o casi elástico, el módulo de Young y la resistencia a la compresión nos permiten tener una idea bastante aproximada de las curvas esfuerzo-deformación, ya que en estos materiales el límite de proporcionalidad, el límite elástico y el punto de ruptura casi son coincidentes. En estos casos, el módulo de Young será muy util para evaluar el comportamiento mecánico de los materiales ante la acción de esfuerzos compresivos de tipo uniaxial.
Las anisotropías estructurales de los materiales, tales como superficies de estratificación o foliación, introducen lógicamente anisotropías mecánicas. Dado que estas superficies introducen debilidades mecáncias (i.e., los materiales se fracturan por extensión y cizalla más fácilmente a favor de las mismas), la resistencia a la compresión y el módulo de elasticidad disminuyen si el esfuerzo principal mayor (i.e., compresor, s1) es paralelo u oblicuo (cercano a 45º) a tales superficies. La resistencia a la compresión de materiales anisótropos es máxima cuando las superficies están orientadas perpendicularmente al esfuerzo principal mayor. Esto es importante en la estabilidad de las estructuras en los edificios y en los trabajos de restauración que impliquen sustitución de piezas por materiales estructuralmente anisótropos.
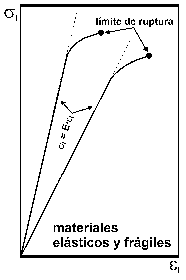

Figura 8. Curvas esquemáticas esfuerzo-deformación para materiales casi-elásticos (e.g., basaltos, granitos de grano fino), semi-elásticos (e.g., calizas, areniscas, mármoles) y plásticos (morteros de cal, morteros de yeso).
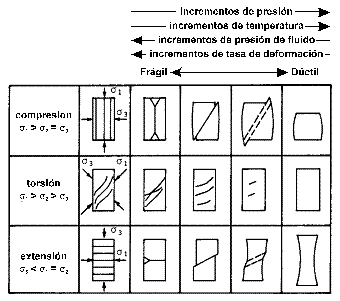
Figura 9. Deformación frágil y dúctil bajo compresión, torsión y extensión (s1, s2 y s3, son los esfuerzos principales mayor, intermedio y menor, respectivamente). Las flechas marcan las tendencias en el comportamiento de los materiales al variar la presión, la temperatura, la presión de fluidos localizados en los poros y la tasa de deformación.
Como se ha indicado más arriba, la presencia de agua en el interior del sistema poroso de un material altera sus propiedades mecánicas. Este efecto se debe dos causas: 1) al desarrollo de presiones hidráulicas en los poros rellenos de agua que afectan a los esfuerzos intergranulares (i.e., contactos de granos), y 2) a la alteración de las propiedades de superficie de los granos (minerales). Esto puede causar inestabilidad a lo largo de superficies más débiles y disminuir la resistencia a la cizalla o fricción, produciéndose una reducción más o menos significativa de su resistencia a la compresión.
La razón entre los coeficientes de resistencia a la compresión del material saturado en agua y seco, denominado coeficiente de ablandamiento, es una medida del efecto del agua sobre la resistencia a la compresión:
![]()
donde: Ks es el coeficiente de ablandamiento (adimensional)
Rs (Pa) es la resistencia a la compresión del material saturado en agua y
Rd (Pa) es la resistencia a la compresión del material seco.
Para algunos materiales muy porosos fácilmente empapables, este coeficiente tiende a 0, ya que Rs tiende a 0, mientras que otros materiales poco porosos como vidrios o aceros el coeficiente de ablandamiento tiende a 1, esto es, retienen sus propiedades mecánicas ante la presencia de agua. Los materiales con coefientes de ablandamiento mayores de 0.8 se califican de resistentes mecánicamente respecto de la acción del agua. Los materiales con coeficientes menores de 0.8 nunca deben exponerse a la acción de la humedad (e.g., zócalos de elementos constructivos que sufren infiltración capilar), y en caso de exponerse, deben aislarse de la humedad con barreras impermeables o tratarse con productos hidrofugantes.
2.2.Resistencia
a la Tension
La resistencia a la tensión es el esfuerzo tensional por unidad de área a la que el material falla (se rompe) por fracturación extensional. Esta propiedad, que es una indicación del grado de coherencia del material para resistir fuerzas “tirantes”, depende de la resistencia de los minerales, del área interfacial entre granos en contacto y del cemento intergranular e intragranular.
Existen distintas técnicas para medir la
resistencia a la tensión, tanto en materiales pétreos como en morteros,
cementos y hormigones. En el ensayo de tracción directa, quizás el más
apropiado, se utilizan probetas cilíndricas con una razón longitud/diámetro de
Los conceptos, definiciones y controles de la
deformación introducidos anteriormente para la resistencia a la compresión
pueden ser extendidos sin más problema a la resistencia a la tensión. Respecto
de los materiales pétreos de construcción, puede generalizarse que, para un
material dado, la magnitud de la resistencia a la tensión suele ser de un orden
de magnitud menor que la resistencia a la compresión. En
|
Tabla 5. Resistencia a la tensión (Mpa) de algunas rocas (de Touloukian y Ho, 1981). Basalto 8.6 Conglomerado 29.7 Calizas 4.2 5.8 Arenisca 1.1 1.7 Arenisca calcárea 4.3 Esquistos 3.1 |
2.3.Resistencia
a la Flexion
La resistencia a la flexión, o módulo de ruptura, es la resistencia de un material a ser doblado (plegado) o flexurado. La medida de esta propiedad se realiza con barras de material asentadas sobre dos pivotes y aplicando carga sobre el centro de la barra (norma ASTM C99-52). La resistencia a la flexión (Sm) viene dada por la expresión:
![]()
donde: P (Pa) es la carga aplicada
l (m) es la distancia entre los pivotes y
d3 (m) es el diámetro de la probeta
si la probeta es cilíndrica, y por la expresión:
![]()
donde: b (m) es el ancho de la sección de la probeta y
h (m) es el largo de la probeta
si la probeta es prismática.
Para un material pétreo dado, el valor de resistencia a la flexión es cercano al doble de su resistencia a la tensión medida con el método de tracción directa.
2.4.Fatiga
Cuando los materiales sufren esfuerzos de forma cíclica sin llegar al punto de ruptura, se observa un debilitamiento mecánico de los mismos con el tiempo. Esto implica una pérdida de sus propiedades mecánicas, que puede dar lugar a la fracturación bajo esfuerzos mucho menores que los apropiados para los materiales “frescos” que no han sido sometidos a esfuerzos. A esta característica de los materiales se le denomina fatiga.
Se ha encontrado que la causa fundamental del fallo por fatiga de los materiales pétreos es la microfracturación. Los experimentos llevados a cabo sugieren una evolución episódica para la fatiga. Inicialmente, se produce una microfracturación entre los contactos de grano y en el interior de los cristales a favor de los planos de exfoliación y superficies de partición de los mismos. A continuación, existe un periodo de aquiescencia, con escasa deformación adicional. En el último estadio, las microfracturas coalescen, perdiéndose coherencia e iniciándose el fallo (fracturación) del material. No obstante, también parece que la fatiga es un proceso continuo, disipándose la energía en forma de microfracturas hasta el punto en que se supera un nivel crítico en el que ocurre el fallo.
La mayor parte de los procesos de deterioro de tipo mecánico que sufren los materiales pétreos en los edificios se deben al fallo por fatiga, ya que los esfuerzos generados no suelen superar la resistencia a la compresión, tensión o flexión de los materiales “frescos”. No obstante, también hay que tener en cuenta el efecto de otros procesos físicos y químicos de alteración, que modifican las propiedades mecánicas originales de los materiales, generalmente reduciendo sus propiedades mecánicas.
Las rocas son materiales con elevada resistencia a la compresión y en menor medida a la flexión y la tensión. Por esta razón son materiales apropiados para elementos constructivos tales como muros, paramentos, columnas, etc., que sufren importantes cargas compresivas, y no tanto para elementos constructivos que sufren importantes esfuerzos tensionales y de flexión, como los generados en estructuras adinteladas o arquitrabadas. Por esta razón, la luz de los arquitrabes no puede ser elevada.
La resistencia a la tensión es una propiedad particularmente importante desde el punto de vista de los procesos de alteración de materiales pétreos de construcción. Esto es debido tanto a la existencia de procesos de alteración cíclicos que generan importantes esfuerzos tensionales capaces de producir fallos mecánicos (fracturación) por fatiga en los materiales, como al hecho de ser la propiedad mecánica cuantitativamente más deficiente en los mismos. Entre los procesos de deterioro mecánico por generación de esfuerzos tensionales cabe destacar los cambios volumétricos que sufren los materiales al sufrir variaciones de temperatura, la formación de hielo y la cristalización e hidratación/deshidratación de sales solubles en el interior del sistema poroso de los materiales.

Figura 10. Acciones mecánicas en el sistema adintelado (modificado de Ortega Andrade, 1993)
2.5.Dureza
La dureza es la resistencia de los materiales para resistir la penetración de otro cuerpo. Para el caso de minerales, la dureza se ha considerado clásicamente como la resistencia que presenta un mineral a ser rayado por otro mineral o material. F. Mohs dedujo empíricamente una escala cualitativa basada en las durezas relativas de distintos minerales que ha sido muy utilizada como criterio de clasificación y de determinación. Esta escala es como sigue:
Dureza Mineral Dureza Mineral
1__________ Talco 6__________ Ortosa
2__________ Yeso 7__________ Cuarzo
3__________ Calcita 8__________ Topacio
4__________ Fluorita 9__________ Corindón
5__________ Apatito 10_________ Diamante
Cada uno de estos minerales es capaz de rayar a los situados antes que él en la escala, y a su vez es rayado por los que vienen después. La medida de la dureza suele ser cualitativa (aunque hay métodos de determinación precisa) estableciéndose en una primera aproximación en base a los siguientes criterios: si la uña raya al mineral la dureza es menor de 2.5; si una navaja raya al mineral la dureza es menor de 5.5; si el mineral raya al vidrio la dureza es igual o mayor de 7. Así, el cuarzo se diferencia de la calcita en que aquel raya al vidrio y ésta no.
Esta propiedad es vectorial, es decir,
depende de la dirección en que se aplique en un mineral, debido a la diferente
distribución de enlaces cristalinos en las estructuras minerales. Así por
ejemplo, la distena (Al2SiO5)
es un mineral de hábito prismático que presenta una dureza de
Aplicadas a los materiales pétreos, esta propiedad es importante para evaluar la trabajabilidad, con utensilios de impacto y abrasivos, de los materiales en la cantera y en la obra. Existen muchos métodos de evaluar la dureza: la resistencia al rayado, a la indentación, a la abrasión, al rebote y al impacto. La gran complejidad de los materiales pétreos no permite una correlación clara entre los distintos parámetros de resistencia mecánica y de dureza, aunque en general, la dureza de los materiales aumenta a medida que la resistencia a la compresión aumenta. Dado que las rocas son materiales frágiles, presenta débil o moderada resistencia al impacto, por lo que son materiales trabajables con herramientas de impacto. Esto permite en la mayor parte de los casos un buen acabado. Lo mismo puede decirse de su buena trabajabilidad por pulido, particularmente en rocas como calizas y mármoles, aunque existen rocas relativamente duras (i.e., aquellas que presentan abundante cuarzo, como cuarcitas y granitos) que resisten bien la raya y la abrasión.
3.Expansión térmica
En general, el incremento de la temperatura de cualquier material produce un aumento de su volumen. Esto se debe a que la energía térmica absorbida induce un incremento en las vibraciones de los átomos constitutivos de la materia, agrandando las distancias interatómicas. Este fenómeno se describe como expansión volumétrica de origen térmico a presión constante, o simplemente expansión térmica, y su medida se realiza en términos del coeficiente de expansión térmica (a). Este coeficiente representa el incremento relativo de volumen producido al aumentar la temperatura en un grado a presión constante, y puede escribirse como:
a = 1/V*(DV/DT)
cuando el incremento de volumen no depende de la temperatura a la que se mida. Las dimensiones de a son ºC-1, y sus valores son positivos en la mayor parte de los casos ya que, como se ha indicado anteriormente, las sustancias suelen aumentar de volumen al aumentar la temperatura. No obstante, existen algunos sustancias que disminuyen su volumen al aumentar la temperatura en determinados rangos de esta última, como es el caso del cuarzo-b (y el agua).
Por lo que se refiere a los minerales cuya estructura cristalina no es cúbica, como es el caso de la mayoría de los minerales que constituyen las rocas comunes, sus coeficientes de expansión térmica dependen de la dirección cristalina en la que se mida (esto es, los minerales son anisótropos respecto de esta propiedad). Así, el cuarzo-a se expande más perpendicularmente a su eje c (eje principal de simetría y de elongación) que paralelamente a él. Este comportamiento se denomina expansión térmica diferencial, y su medida se realiza en términos de coeficientes de expansión térmica lineal (l), que representan los incrementos relativos de longitud producidos al aumentar la temperatura en un grado a presión constante:
l = 1/l*(Dl/DT)
La dimensión de este coeficiente es también ºC-1, y sus valores son positivos en la mayor parte de los casos por la misma causa que se ha indicado más arriba. No obstante, existen algunas sustancias que disminuyen su longitud en direcciones determinadas al aumentar la temperatura, como en el caso de la calcita, que se expande paralelamente a su eje c y se contrae perpendicularmente a él. No obstante, el coeficiente de expansión térmica de la calcita en términos de volumen es positivo, ya que la contracción que sufre perpendicularmente al eje c es proporcionalmente menor a la expansión que sufre paralelamente al mismo. En el caso del cuarzo-b, el incremento de temperatura supone contracciones en todas las direcciones cristalográficas, por lo que el resultado neto es un descenso de volúmen (o aumento de densidad).


Figura 11. Expansión térmica volumétrica y lineal de algunos minerales formadores de rocas (tomado de Winkler, 1973).
Tabla 6. Expansión térmica lineal y
volumétrica del cuarzo desde
Temperatura ( ºC) Incremento de l (%) Incremento de volumen (%)
^ c // c
50________________ 0.07____________ 0.03_____________________ 0.17
100________________ 0.14____________ 0.08_____________________ 0.36
200________________ 0.30____________ 0.18_____________________ 0.78
300________________ 0.49____________ 0.29_____________________ 1.27
400________________ 0.72____________ 0.43_____________________ 1.87
500________________ 1.04____________ 0.62_____________________ 2.70
570________________ 1.46____________ 0.84_____________________ 3.76
573 Transición de cuarzo-a a cuarzo-b
580________________ 1.76____________ 1.03_____________________ 4.55
600________________ 1.76____________ 1.02_____________________ 4.54
700________________ 1.75____________ 1.01_____________________ 4.51
800________________ 1.73____________ 0.97_____________________ 4.43
900________________ 1.71____________ 0.92_____________________ 4.34
1000________________ 1.69____________ 0.88_____________________ 4.26