Antonio García Casco

[CV] · [Petrogénesis metamórfica] · [Cristalquímica básica] · [Advanced Petrology · IPGP] · [IUGS_SCMR] · [Geotermobarometría] · [Curso: Metamorfismo como herramienta geodinámica] · [Análisis de Sistemas Heterogéneos] · [CSpace] · [EPMA-SEM] · [Imágenes de RX] · [Prop Fisicoquímicas de los Magmas] · [Tutor de Petrología] · [Trabajo de Campo de Petrología] · [Glosario de Geología (RAC)] · [Restauración de Monumentos] · [Rocas y Minerales] · [Las rocas hacen ciudad, Granada] · [Grupo de Petrología Geoquim y Geocron (SGE)] · [Research Group RMN302] · [IGCP 546 Caribbean Subduction] · [TFF 2025 Cuba] · [Biblioteca Digital Cubana de Geociencias] · [Enlaces de interés] · [Notas de Prensa]

Microscopía electrónica > Cuantificacion

[Intro] [Interacciones e-muestra] [EPMA] [SEM] [Fuentes de emisión] [El haz] [Muestras] [SE] [BSE] [CL] [EBSD] [RX] [Ley de Bragg] [WDS] [EDS] [Mapas de RX] [Detectores] [Cuantificación de la señal] [Datación monacita] [Manual de procedimientos]

Texto tomado fundamentalmente de

Reed, Stephen J.B., 2006. Electron Microprobe Analysis and Scanning Electron Microscopy in Geology, 2e édition. Cambridge University Press, Cambridge, 206 p.

Xavier Llovet, Aurélien Moy, Philippe T. Pinard, John H. Fournelle (2021). Electron probe microanalysis: A review of recent developments and applications in materials science and engineering. Progress in Materials Science 116, 100673.

Cuantificación de la señal

Los RX característicos de un elemento dado se dirigen a un detector de rayos X (dentro junto al espectrómetro y de la configuración geométrica del círculo de Rowland ) donde se produce una señal eléctrica (generalmente, en un contador de flujo continuo de gas). Esta señal es proporcional al número de rayos X, que a su vez es proporcional a la concentración del elemento "i" en la muestra. La señal eléctrica se amplifica y se compara con la señal producida en las mismas condiciones por un estándar de composición conocida. La concentración final del elemento "i" en la muestra se calcula basándose en la proporcionalidad entre la intensidad de los rayos X en la muestra desconocida y la intensidad de los rayos X producida por el estándar conocido, siguiendo un procedimiento de corrección para minimizar el efecto "matriz" en la medición.

El espectro de rayos X se utiliza para análisis cuantitativos midiendo la intensidad de los picos característicos de rayos X correspondientes a diferentes elementos de la muestra siguiendo los siguientes pasos:

1. Identificación y medición de la intensidad de pico: El primer paso consiste en identificar los picos característicos en el espectro, que corresponden a elementos específicos. El software de las máquinas permite identificar automáticamente los picos y, en general, deconvolucionar con precisión los picos superpuestos mediante métodos matemáticos. Se calcula la intensidad (cuentas por segundo por nanoamperio) de los picos característicos de un material dado mediante los detectores de RX característicos difractados. La intensidad está directamente relacionada con la abundancia de los elementos correspondientes en la muestra.

2. Sustracción de fondo: El fondo continuo, correspondiente a la radiación de frenado (Bremsstrahlung), se sustrae del espectro para medir con precisión las intensidades de los picos característicos.

3. Estandarización y calibración: El análisis cuantitativo requiere calibración con estándares de composición conocida para comparar sus picos con los de la muestra. Estos estándares ayudan a controlar la calidad de los cristales analizadores y detectores (en EDS, determinar la eficiencia del detector).

4. Corrección de efectos de matriz: Se aplican correcciones para tener en cuenta los efectos de matriz ZAF, que incluyen efectos de número atómico (Z), absorción (A) y fluorescencia (F) que alteran la intensidad de los rayos X. Estas correcciones garantizan que las intensidades medidas reflejen con precisión las concentraciones reales de los elementos.

5. Cálculo cuantitativo y criterios de calidad: Utilizando las intensidades de pico corregidas y los datos de calibración, se calcula la concentración de cada elemento en la muestra. Esto puede realizarse mediante diversos algoritmos cuantitativos y el software incluido con el sistema.

1a.- Identificación y medición de picos

Lo ideal sería recopilar la señal total de cada pico integrando todos los canales (longitudes de onda) bajo él. Para WDS, esto implicaría un barrido angular del espectrómetro, lo que resulta demasiado lento para la adquisición de datos cuantitativos o el mapeo de rayos X. Por lo tanto, se mide un único canal centrado en el pico y se asume que es representativo del área total bajo el pico (en EDS se mide el área integrada del pico).

Espectros de RX difractados por TAP y PET en material cerámico con Si, Al, Fe, Sn, Zr (Jeol).

La intensidad de los rayos X producidos por el elemento “i” en la muestra se puede expresar como el número de rayos X contados por segundo (cuentas/seg = cps) por el detector. Se conoce la longitud de onda de los rayos X característicos de todos los elementos, así como el senoӨ (Ө es el ángulo de difracción para un plano de espaciado dado, según la ley de Bragg). Las sondas Cameca controlan el movimiento del espectrómetro y la indexación de rayos X basándose en valores de senoӨ. Las sondas JEOL funcionan con el valor “L”, donde L es la longitud que conecta la muestra con el cristal analizador (o sea, la longitud recorrida por el rayo X difractado desde la muestra hasta el cristal analizador), L = 2R·senoӨ, siendo R el radio del círculo de Rowland (160 mm para las sondas Cameca y de 140 mm para las sondas JEOL, excepto para los espectrómetros “H” en las sondas JEOL, que tienen R=100 mm). Al ajustar la posición del cristal analizador a un valor único de “sinӨ” o “L” para un elemento “i”, el cristal analizador difractará únicamente los rayos X de longitud de onda característica provenientes del elemento “i” (esto sucede porque los rayos X que tienen una longitud de onda similar al espaciamiento d de la red cristalina del cristal analizador serán refractados). Este es el principio que hizo posible la invención de la microsonda electrónica por el estudiante de doctorado francés Raymond Castaing en 1952. Los rayos X producidos por el elemento “i” pueden así contarse durante un período de tiempo específico (“tiempo de contaje”). Dado que el cristal de un espectrómetro WDS solo puede registrar conteos de rayos X para una longitud de onda a la vez, el análisis de múltiples elementos en un solo espectrómetro debe realizarse secuencialmente, comenzando por los elementos de Z menor como el Na que puede verse afectados por difusión fuera del volumen irradiado por fuerzas electrostáticas acumuladas. Además, dado que ningún tipo de cristal puede satisfacer la Ley de Bragg para todo el rango de longitudes de onda de rayos X emitidos por todos los elementos de la tabla periódica, las microsondas electrónicas están equipadas con varios espectrómetros (4-5), con la capacidad integrada de intercambiar automáticamente diferentes cristales analizadores dentro de un mismo espectrómetro (generalmente, hasta diez cristales difractores en total para registrar todos los elementos deseados con Z ≥ 4). Todo ello ralentiza la adquisición de datos para el análisis (generalmente, unos 5-10 minutos por análisis puntual).

1b.- Interferencias espectrales y superposiciones

En ocasiones, las intensidades de los picos se ven potenciadas por la superposición de un pico vecino. Las interferencias espectrales son un problema para EDS- y WDS-EPMA (y SEM-EDS), ya que difuminan los picos elementales de rayos X de interés, requiriéndose una corrección de superposición. En cualquier caso, las interferencias pueden resolverse mejor en WDS que en EDS, dada la mayor resolución de energía

La cantidad de superposición puede expresarse como una fracción de la intensidad del pico principal del elemento superpuesto. En EDS esto afecta a toda el área debajo de la curva del pico. Con WDS, el aumento de la resolución espectral reduce muchas de estas interferencias ya que trabaja con canales estrechos de longitud de onda. Pero, a diferencia de EDS, el uso de la difracción de Bragg para WDS genera problemas de "n mayor que uno", por lo que los espectros de WDS contendrán cierta cantidad de estos picos de alto orden de difracción (n > 1). A veces, pueden coincidir con un pico objetivo o muy cerca de él, con una longitud de onda más baja o más alta, y potencialmente ser convertirse en interferencia para la medición del fondo.

Distintas respuestas de interferencia (rojo) en función de la posición de los picos de elemento medido (verde) y del elemento interferente (azul). Las respuestas se deben a la suma de intensidades de longitud de onda de los elementos medido e interferente. Una vez superada cierta separación de picos (Dl3), no hay interferencia en el pico del elemento analizado.

Se utilizan varios métodos para corregir las interferencias espectrales. El método más sencillo consiste en medir la intensidad de los rayos X en la posición (longitud de onda) de la línea superpuesta (p.ej., V ka) en una muestra de referencia (patrón, por ejemplo, Ti puro) que contiene el elemento que se superpone (p.ej., Ti), pero no el superpuesto (p.ej., V). Esta intensidad se resta de la intensidad medida en el elemento desconocido en una proporción constante, que debe calcularse del análisis del patrón. Por ejemplo, la presencia de Ti oscurecerá la  concentración de V en una muestra que contenga ambos elementos ya que V Ka se ve interferida por Ti Kb. La interferencia V Ka - Ti Kb se resuelve midiendo las intensidades de Ti Ka y Ti Kb en un patrón (Ti puro) y en el material desconocido que contiene V de forma que, dado que la relación de intensidades de Ti Kb y Ti Kb es la misma en ambas matrices:

(I TiKb/I TiKa)^PATRON = (I TiKba/I TiKa)^DESCONOCIDO = constante

la intensidad real V Ka en el material desconocido es:

I VKa^REAL = I VKaTiKb^MEDIDA - I TiKb^DESCONOCIDO

I VKa^REAL = I VKaTiKb^MEDIDA - [I TiKa^DESCONOCIDO · (TiKb/TiKa)^PATRON]

siendo (TiKb/TiKa)^PATRON el factor de intensidades e VKaTiKb^MEDIDA la intensidad medida en la línea interferida, por oposición a la real.

Así, en general, los factores de intensidades pueden determinarse a partir de patrones de elementos puros, y la intensidad real de la línea interferida se encuentra restando de la intensidad medida lo calculado utilizando una intensidad de referencia del elemento que interfiere y el factor de intensidades del patrón:

I^REAL = I^MEDIDA - [I^{DE REFERENCIA DESCONOCIDO} · Factor de Intensidades^PATRON]

Lo anterior aplica a espectros EDS y WDS, si bien, como se muestra más abajo, en WDS puede que no hiciera falta la corrección por interferencias ya que la resolución de energía de éste último método es mucho mayor, pudiendo resolverse las medidas de interés en el espectro WDS de forma satisfactoria.

Espectro EDS de una aleación Ti-6Al-4V que muestra la superposición observada entre las líneas Ti Kb (4.932 keV) y V Ka (4.952 keV) (de Oxford Instruments). En EDS es imposible resolver la interferencia.

Barrido de longitud de onda WDS (expresado en energía) para la aleación Ti-6Al-4V mostrando picos distintivos de Ti Kb y V Ka (morado). El espectro EDS se muestra al fondo (amarillo) para fines comparativos. Como la resolución de energía de WDS es 10 veces mejor que la de EDS, los picos superpuestos de Ti y V se pueden diferenciar y las concentraciones de estos elementos se pueden determinar con mayor precisión (de Oxford Instruments).

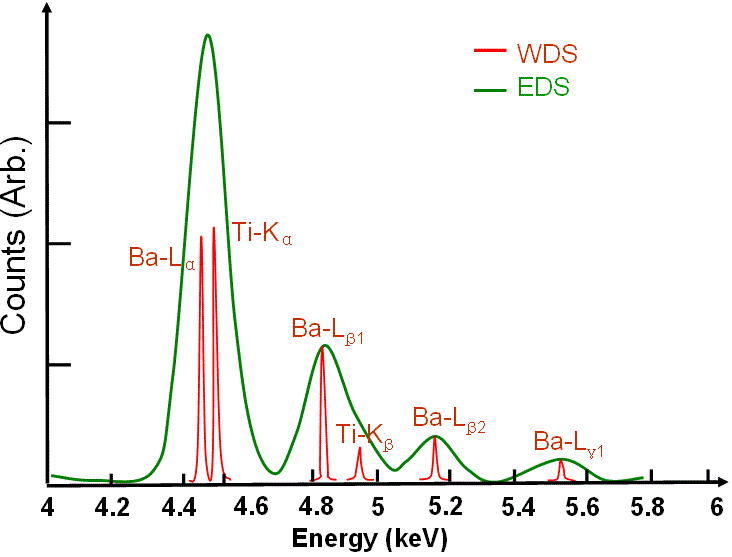
Interferencia Ti-Ba Espectro EDS de BaTiO₃ con solapamiento de picos EDS que se resuelven en WDS dada su mayor resolución de energía (5-10 eV) (de Liao 2006).

Sección del espectro de rayos X de galena en la región de energía de 2.2 a 2.6 keV que muestra la alta resolución espectral de WDS en comparación con EDS (de Bruker)

Espectro WDS simulado para monacita que muestra un alto número de solapamientos de líneas de pico entre los elementos de las tierras raras. Se ha seleccionado la posición de pico del praseodimio (Pr Lb, menos intenso que Pr La) para evitar el solapamiento de los picos La Lβ y Pr Lα (de Oxford Instruments).

Otros métodos más precisos incluyen la deconvolución espectral, utilizando un espectro adquirido en una muestra de referencia conocida que no contiene el elemento superpuesto. Por ejemplo, en un espectro U-Pu, la línea de rayos X Pu Mβ se superpone con la línea U M3N4 de baja intensidad (tenga en cuenta que la línea de rayos X Pu Mα no puede utilizarse para el análisis debido a la fuerte interferencia con la línea de rayos X U Mβ). La deconvolución, utilizando el espectro medido a partir de un estándar de UO₂ y escalado adecuadamente, permite una medición precisa de la intensidad Pu Mβ.

Las reflexiones Bragg de orden superior (n > 1) no deben ignorarse ya que potencialmente constituyen una fuente de interferencia espectral. Pueden generar problemas críticos para el trabajo con elementos traza. En general, es posible minimizar la influencia de los picos de difracción de orden >1 hasta en un ~90 % mediante el ajuste adecuado de una ventana de energía en los contadores de RX (PHA, Pulse Height Analyzer), si bien debe evitarse la supresión involuntaria de la altura del pulso de picos n = 1.

Armónicos de orden de difracción 1 y 2 en cobre difractado por el cristal LiF (2d = 0.4026 nm), expresado en cuentas por segundo en función del ángulo de difracción). Nótese que tanto para n = 1 como n = 2, la longitud de onda y la energía de Kα = 1.54 A = 8.06 keV y de Kβ = 1.39 A = 8.92 keV (de physicsopenlab.org).

Las interferencias de pico deben corregirse, y el método más preciso requiere iterarlas dentro de la corrección de matriz, en lugar de restarlas como una corrección posterior a la corrección de matriz ZAF (o PAP).

1c.- Elementos traza

Los elementos traza pueden determinarse en roca-total mediante técnicas de análisis químico como XRF, ICP-MS, etc. Sin embargo, para determinar su distribución en las diferentes fases del material, se requiere una técnica de análisis de microhaz como EPMA o LA-ICP-MS.

La emisión de Bremsstrahlung o de frenado se produce cuando el los electrones incidente desaceleran al interactuar con el campo electrostico que rodea los átomos de objetivo, perdiendo energía en forma de rayos X emitidos y creando una señal continua de fondo de rayos X (hasta el límite de Duane-Hunt, que coincide con la energía E₀ de los electrones incidentes). Esta radiación de frenado es el factor limitante para la detección de elementos traza ya que el fondo generado puede ocultar los picos característicos de estos elementos.

La cantidad de radiación de fondo aumenta con la densidad de la muestra, lo que significa que los elementos ligeros en una matriz pesada pueden ser difíciles de detectar. La forma de la radiación de fondo, descendiendo de intensidad hacia altas energías, hace que los elementos en traza pesados puedan detectarse con mayor facilidad que los ligeros.

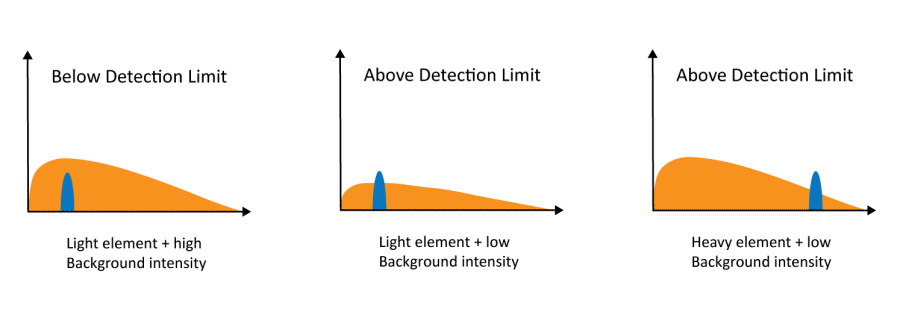
El espectro de rayos X está compuesto por picos de rayos X característicos y un fondo continuo conocido como Bremsstrahlung (radiación de frenado). La intensidad del fondo está determinada por la densidad de la muestra. Por ello, puede ser difícil detectar trazas de elementos ligeros en una muestra con una matriz de elementos pesados. De Nanoscience Instruments.

El parámetro más importante para el análisis de trazas es el límite de detección. Se trata de cuanto de pequeña puede ser una variación estadística normal del fondo para poder identificarla con un pequeño pico característico. Por tanto, el análisis de trazas mediante EPMA necesita una resolución espacial muy alta y una alta sensibilidad. Esto presenta numerosos desafíos, si bien la precisión no es el mayor obstáculo, porque los instrumentos modernos ofrecen una buena eficiencia de recolección de RX y una corriente de sonda alta y estable, lo que permite adquisiciones prolongadas. La resolución espacial del análisis puede extenderse muy por debajo de 1 μm en análisis de bajo voltaje (por debajo de 15 kV) de fases de alto número atómico promedio. El uso de alta corriente de sonda y/o un tiempo prolongado de exposición del haz para lograr análisis de alta sensibilidad puede agravar los efectos de daño y carga, especialmente en materiales aislantes como las rocas/minerales, lo que puede comprometer la precisión. Un voltaje más alto mitiga parte de esto y aumenta las tasas de conteo, pero las desventajas obvias son la menor resolución espacial y las altas correcciones de la matriz.

El análisis de trazas mediante EPMA es fundamentalmente una caracterización y medición del fondo, ya que pequeñas imprecisiones en la determinación del fondo producen grandes errores en la intensidad neta. La curvatura de fondo y las interferencias hacen que la interpolación lineal simple de 2 puntos sea inadecuada (especialmente en materiales complejos), lo que puede resultar en errores de decenas a cientos de ppm.

De M J Jercinovic, M L Williams, J Allaz y J J Donovan (2012). Trace analysis in EPMA.

La intensidad de los rayos X viene regulada por la sobretensión (U), dado que la probabilidad de emisión de rayos X aumenta a medida que aumenta la tensión de aceleración (voltaje). La relación pico-fondo P/B de un material dado utilizando un cristal WDS dado (o un detector EDS específico) puede aproximarse mediante:

P/B = 1/Z(U-1)ⁿ

donde U es la relación de sobretensión (E₀/E_c) y n es un exponente que normalmente se encuentra en el rango de 0.3 a 0.7. De esta ecuación se deduce que la relación pico-fondo P/B aumenta al aumentar la tensión de aceleración. Por lo tanto, al operar el instrumento EPMA con una sobretensión alta, se puede superar el límite de detección para una corriente de sonda y un tiempo de contaje determinados será menor. Cabe destacar que los dos últimos factores (corriente de sonda y tiempo de contaje) determinan la precisión de los análisis, y es la reducción de la variabilidad analítica del fondo la que permite medir con precisión concentraciones muy pequeñas. WDS tendrá límites de detección más bajos que el EDS, debido a su mejor resolución espectral y, por consiguiente, a una mayor relación pico-fondo.

Relaciones cualitativas Pico/Fondo (P/B) en función del número atómico y el sobrevoltaje.

En general, usando energía estándar (15-30 keV), el análisis de elementos en traza necesita de

• alta corriente sonda (varios cientos de nA y hasta algo más de mil nA,

• altos tiempos de contaje de pico (centenas de segundos) y

• deben agregarse los datos de varios espectrómetros (más de un espectrómetro midiendo al mismo tiempo el mismo elemento)

para alcanzar límites de detección de varias unidades a decenas de ppm. Vea, p.ej.,  Dominguez-Carretero et al. (2025) Accurate electron probe microanalysis of key petrogenetic minor and trace elements in Cr-spinel,  10.1016/j.chemgeo.2024.122579.

Para evaluar la precisión de los análisis de trazas en EPMA, es habitual comparar los resultados con los de otras técnicas microanalíticas, como PIXE, μ-XRF, SIMS o LA-ICP-MS. Por ejemplo, Sobolev et al. 2007 midieron sistemáticamente varios elementos traza en olivino de rocas basáticas para investigar la contribución de fuentes corticales recicladas en el manto. Estos autores analizaron más de 17000 granos de olivino y reportaron límites de detección de 6 a 15 ppm y errores de 15 a 30 ppm (a nivel 2σ) para los elementos Ni, Ca, Mn, Cr, Co y Al. La precisión de los resultados de EPMA se evaluó comparándolos con los resultados de LA-ICP-MS. Un procedimiento similar ofrecen Dominguez-Carretero et al. (2025) para elementos traza en cromititas.

Precisiones analíticas (2s) para Ti, V, Ni y Mn y (b) límites de detección (3s) para Sc, V, Ti, Mn, Co, Ni, Zn y Ga, obtenidos sobre un patrón de referencia de Cr-espinela en función de la corriente de sonda, a 25 keV y tiempos de contaje de pico y fondo de 60 y 30 segundos, respectivamente. Dominguez-Carretero et al. (2025).

1d.- Tiempo muerto

Dado que la electrónica tarda un tiempo finito (del orden de microsegundos) en procesar un evento (detectar un pulso generado por rayos X), existe un período en el que está "ocupado" con una señal y debe ignorar las demás. Por lo tanto, el detector es ciego a la llegada de nuevos fotones durante este "tiempo muerto". Los tiempos muertos típicos están en torno a unos pocos ms (microsegundos).

Cuando la tasa de la señal de rayos X es baja, es improbable que llegue un segundo fotón durante el tiempo "ocupado". Cuando la tasa de la señal es alta, una fracción significativa del tiempo real se dedica al procesamiento de eventos y esta fracción de tiempo real se registra tiempo muerto. El software corrige los conteos medidos para el tiempo muerto.

Todos los sistemas de detección de rayos X deben incluir en sus esquemas de cuantificación una corrección del tiempo muerto; es decir, tener en cuenta la incapacidad de la electrónica del detector para contabilizar correctamente cada rayo X, debido a la fracción finita de tiempo en la que el sistema está "ocupado" y no detecta rayos X. Los fabricantes de instrumentos de sonda electrónica proporcionan una "constante de tiempo muerto" para cada espectrómetro/detector suministrado. Sin embargo, para una cuantificación precisa, algunos laboratorios de sonda electrónica han determinado valores más precisos para sus instrumentos específicos y han descubierto que los valores de tiempo muerto cambian con el envejecimiento del instrumento y no son constantes para todas las corrientes de haz/velocidades de conteo.

El tiempo muerto definido como el intervalo de tiempo (t) tras la llegada de un pulso durante el cual el sistema no responde a pulsos posteriores (normalmente unos pocos microsegundos), hace que la tasa de conteo medida (n') sea menor que la tasa de conteo real (n) en una cantidad que se vuelve significativa a tasas de conteo altas, según la ecuación:

n' = n(1-n·t)

Las intensidades medidas pueden corregirse por tiempo muerto aplicando esta ecuación. Por ejemplo, con un tiempo muerto típico de 3 ms (30^-6 s), la medición de 30000 cuentas/s supone corregir en 10% (3000 cuentas/segundo), o sea, las cuentas reales serían 33000 cuentas/s.

Intensidades reales vs medidas en función del tiempo muerto.

2.- Modelado y sustracción del fondo

El análisis cuantitativo con microsonda se basa en la comparación entre a) la intensidad medida (cps netas, I_i^unk) de los rayos X de cada elemento “i” presente en una muestra desconocida, y b) la intensidad medida (cps netas, I_i^std) de los rayos X del mismo elemento “i” en un material estándar cuya concentración se conoce. Pero la intensidad de pico medida incluye una contribución del fondo, originada principalmente en el continuo de rayos X. Por ello, la comparación debe realizarse entre las intensidades netas de los rayos X en el elemento desconocido y el estándar durante el “tiempo de contaje”, donde la intensidad neta (I_i) es la diferencia entre la intensidad de pico total (IP_i) y el promedio de las intensidades de los fondos inferior y superior (IB_i), tanto en el estándar como en la muestra desconocida:

I_i^unk = IP_i^unk - IB_i^unk

I_i^std = IP_i^std - IB_i^std

El fondo varía lentamente en función de la longitud de onda y puede estimarse tomando el promedio de las mediciones a cada lado del pico (fondo inferior y superior). La curvatura del fondo es insignificante para la mayoría de los propósitos, pero puede ser significativa en la región de la cola de un pico principal vecino. Si las mediciones de fondo aumentan por la superposición de un pico vecino, la intensidad aparente pico-fondo es demasiado baja e incluso puede ser negativa. Este efecto puede evitarse midiendo el fondo solo en un lado, donde no hay superposición pero debe tenerse en cuenta la pendiente. La cola del pico adyacente se puede representar mediante polinomios de orden variado.

Fondo determinado promediando las intensidades medidas en posiciones de desplazamiento (fondo1 y fondo2): (a) fondo lineal: se obtiene el resultado correcto para el fondo bajo el pico; (b) fondo curvo: se obtiene un resultado incorrecto si se interpola linealmente (Reed, 2006).

El procedimiento estándar para obtener la intensidad neta de pico en una medición WDS consiste en registrar la tasa de conteo en el canal correspondiente al centro/máximo del pico y, habitualmente, aunque no siempre, en dos posiciones de fondo a ambos lados del pico (se permite usar solo un lado si las condiciones lo requieren y es posible modelar el fondo correctamente). La intensidad de fondo en la intensidad máxima del pico se obtiene mediante la interpolación de las mediciones de fondo. De forma óptima, el software permite diferentes opciones de modelo de fondo, desde lineal hasta curvo/exponencial y con pendiente, que se resta de la tasa de conteo medida. Este procedimiento proporciona, en general, resultados precisos gracias a la alta relación pico-fondo de los espectros WDS.

La sustracción precisa del fondo es fundamental, en particular para las concentraciones menores y traza. El continuo en el espectro WDS no es necesariamente una línea recta de un extremo al otro, sino que puede mostrar una curvatura de leve a significativa. Un modelado adecuado del fondo es fundamental. Hay dos cuestiones:

(i) Puede haber interferencias de primer orden o de orden superior en las posibles ubicaciones del fondo, que deben evitarse. No existe una regla que indique que se debe colocar una posición de fondo en el lado inferior y otra en el lado superior del pico. Es perfectamente correcto tener dos fondos en un lado del pico. La única regla es que el modelo de fondo bajo la posición característica del pico debe ser coherente con la forma/pendiente del fondo a medida que transita de un lado al otro del espectro.

(ii) No todos los fondos son lineales, y muchos, especialmente en el extremo inferior del espectro, son curvos.

Por lo tanto, es esencial que el software utilizado sea capaz de proporcionar cierto grado de curvatura en el modelo de fondo. Obviamente, si el fondo es curvo, no se puede asumir que es recto (se determinaría un fondo incorrecto, demasiado alto, lo que resultaría en una subestimación de la intensidad neta y, por lo tanto, de la concentración).

Espectros de longitud de onda representativos alrededor de los picos de interés obtenidos en uno de los granos de Cr-espinela adquiridos en las condiciones indicadas en cada panel con indicación de las posiciones donde se midió el fondo. Domínguez Carretero et al. (2025). Accurate electron probe microanalysis of key petrogenetic minor and trace elements in Cr-spinel.

Para un rango limitado de mediciones, por ejemplo, elementos mayores Si, Ti, Al, Fe, Mn, Mg, Ca, Na y K en silicatos comunes se puede determinar fácilmente un conjunto rutinario de compensaciones del fondo. Pero para materiales no comunes es fundamental determinar las compensaciones óptimas de fondo caso por caso mediante la adquisición de escaneos de longitudes de onda, aunque programas como "Virtual WDS" y la "herramienta de desarrollo de métodos EPMA" pueden simplificar la tarea.

3.- Calibración y comparación con estándar (razón k)

Castaing sentó las bases del análisis cuantitativo en EPMA reconociendo que con esta técnica era esencial medir la intensidad de los rayos X de un material de referencia estándar utilizando exactamente el mismo equipo y las mismas condiciones analíticas que para medir el material desconocido, lo que llevó a definir la razón k.

Para cualquier elemento “i”, la razón entre la intensidad neta del elemento “I_i^unk” en la muestra desconocida y la intensidad neta del elemento “I_i^std” en el estándar (I_i^unk/I_i^std) se conoce como razón k_i. Por lo tanto, la concentración (% peso) del elemento “i” en la muestra desconocida (C_i^unk) se da con la aproximación conocida como Primera Aproximación de Castaing:

Por ejemplo, si en las mismas condiciones obtenemos una intensidad neta de 20,000 cuentas/seg para Fe en una muestra desconocida y 40,000 cuentas/seg para Fe en un estándar que contiene 50 % en peso de Fe, en una primera aproximación, el contenido de Fe en la muestra desconocida se calcula como:

(20,000/40,000) * 50 % en peso de Fe = ½ * 50 = 25 % en peso de Fe.

Castaing, además de crear la primera sonda electrónica operativa, desarrolló el procedimiento analítico utilizando metales elementales puros como patrones y relacionando el contaje de rayos X de un elemento en la aleación desconocida con el contaje de rayos X del metal elemental puro. El uso de estos patrones de referencia en EPMA es fundamental para la precisión de las mediciones de materiales desconocidos. Diversas agencias han definido la terminología de los patrones (p. ej., el Instituto Nacional de Estándares y Tecnología de EE. UU., el Comité Conjunto de Guías en Metrología)

Para el microanálisis, un Material de Referencia se define como un material suficientemente homogéneo (es decir, a escala micrométrica) y estable bajo el haz de electrones. Su composición química debe conocerse, preferiblemente mediante una técnica diferente (p. ej., análisis químico húmedo, XRF, etc.). Un Material de Referencia Certificado es un Material de Referencia (MR) que se acompaña de un certificado que proporciona la composición química, la incertidumbre asociada y una declaración de trazabilidad metrológica. Algunas agencias, como el NIST, pueden proporcionar niveles de certificación adicionales, por ejemplo, el Material de Referencia Estándar del NIST. Normalmente, en la ciencia de los materiales, se utilizan metales de pureza definida en muchas aplicaciones; también se utilizan compuestos binarios y ternarios (por ejemplo, semiconductores). Además, se utilizan boruros, carburos, nitruros y óxidos. Para los casos en que se analizan silicatos, carbonatos, fosfatos y otros materiales cristalinos, se utilizan como estándares muchos minerales naturales y sintéticos. Diversos vidrios de referencia también son útiles como estándares.

Existen diversas fuentes de estándares microanalíticos; por ejemplo, varios proveedores de de microscopía electrónica o institutos gubernamentales de estándares venden bloques montados. Estos deben ir acompañados de la documentación correspondiente que indique la composición y la fuente. También se pueden adquirir granos individuales, montarlos y pulirlos adecuadamente. El uso y cuidado adecuados de los estándares microanalíticos a veces no se valora lo suficiente. En general, la coincidencia de matrices de los estándares con las muestras desconocidas es esencial para el análisis EPMA de compuestos que combinan elementos de bajo y alto Z.

Vea también apéndice en Llovet et al. (2021).

4a.- Corrección de matriz ZAF

En la práctica, la primera aproximación de Castaing debe corregirse para tener en cuenta los efectos de otros elementos presentes en la muestra (y el estándar), que pueden afectar de forma diferencial la producción de rayos X (es decir, efectos de la matriz). La corrección de los efectos de la matriz más común se denomina corrección ZAF y fue propuesta por primera vez por Castaing. Esto significa que la concentración del elemento "i", calculada mediante la primera aproximación, debe multiplicarse por el cociente ZAF, donde:

Z es un factor de corrección para diferentes elementos con diferente número atómico Z presentes en la muestra desconocida y el estándar.

A es un factor de corrección para la absorción diferencial de rayos X.

F es un factor de corrección para la generación diferencial de fluorescencia secundaria.

El punto de partida de un método cuantitativo es establecer la relación entre la intensidad de rayos X y la concentración de elementos. Esto puede lograrse con dos enfoques diferentes:

(i) integrar cada contribución a lo largo de la trayectoria del electrón y considerar la pérdida de generación de rayos X debido a la retrodispersión de electrones, y

(ii) integrar cada contribución a lo largo de la profundidad de la muestra, siempre que se conozca la distribución de la emisión de rayos X en profundidad.

El primer enfoque es la base de los métodos ZAF, mientras que el segundo se utiliza en los métodos f(rz). Si bien las correcciones ZAF aún están disponibles en algunos sistemas/microsondas, existe una tendencia general a reemplazarlas por correcciones f(rz) más avanzadas.

Aquí se considerarán de forma cualitativa las correcciones ZAF. El factor de retrodispersión (Z) representa la pérdida de intensidad de rayos X debido a los electrones retrodispersados, el factor de absorción (A) corrige los rayos X generados en la muestra pero que no pudieron escapar de ella y el factor de fluorescencia (F) representa los rayos X generados no por el impacto de electrones primarios, sino por la fluorescencia de rayos X característicos primarios y de fotones de frenado. La corrección por absorción suele ser la más significativa, especialmente en el análisis de elementos ligeros, mientras que el factor de fluorescencia F suele ser el menos significativo de los tres factores de corrección. Estos factores tienen formulaciones matemáticas complejas que necesitan de métodos de iteración para ser resueltas (Vea Llovet et al., 2021 para las expresiones matemáticas y su apéndice).

El factor de corrección "Z"

Los electrones incidentes pierden energía en interacciones inelásticas con los electrones de la capa interna de la muestra dentro del volumen analítico (o volumen de interacción entre los electrones del haz y la muestra). Un material con un Z medio alto tiene una densidad más alta y una configuración electrónica más compleja que un material con un Z medio más bajo. Esto significa que, para el mismo voltaje de aceleración, la profundidad a la que los electrones del haz pueden penetrar en un material con Z medio alto es menor que la profundidad de penetración de los materiales con un Z medio más bajo. El llamado "poder de frenado" (energía perdida por los electrones del haz por unidad de masa penetrada, o espectro continuo) no es constante, sino que disminuye al aumentar Z. Esto tiene como consecuencia la producción de un mayor número de electrones retrodispersados ​​en materiales con Z medio alto y, en consecuencia, un menor número de eventos de dispersión de rayos X. Por otro lado, incluso con un menor número de interacciones de dispersión de RX en los materiales con un Z más alto, las capas electrónicas más complejas de los elementos con un Z más alto provocarán una mayor cantidad y una familia más amplia de rayos X (por ejemplo, valores significativos de Lα, Lβ, Mα, Mβ) en comparación con un elemento con un Z más bajo. Si tanto Si como Fe están presentes en la misma muestra con igual concentración, el número de rayos X producidos por uno y otro sería diferente y, por lo tanto, el resultado de la primera aproximación de Castaing debe corregirse. Esta corrección tiene dos componentes: corrección por el "poder de frenado" y corrección por la "retrodispersión". Si el Z medio de la muestra desconocida es mayor que el del estándar, se debe aplicar una corrección a la baja en la composición.

Factor de corrección “A”

Algunos rayos X generados en el volumen analítico no escapan de la muestra y son absorbidos por todos los elementos presentes en diferente medida y en todas las direcciones de propagación. La absorción a lo largo del camino hacia los detectores de rayos X y la longitud de dicho camino requieren una corrección de la intensidad medida (es decir, emitida) para obtener la intensidad inicial (es decir, generada) de los rayos X. Esta corrección se denomina corrección de absorción (A).

Factor de corrección “F”

Los rayos X generados por un elemento dado, con una energía cercana o superior a la energía crítica de excitación de otro elemento, al salir del volumen analítico, pueden eliminar un electrón de una capa externa. Dado que la vacante creada de esta manera siempre estará ocupada por un electrón de una capa externa uniforme, se emitirá un fotón y, por lo tanto, se producirá un rayo X. Este fenómeno se conoce como fluorescencia secundaria. Por lo tanto, los rayos X de alta energía de un elemento "i" fluorescen los rayos X del otro elemento "j" y acentúan la intensidad de los rayos X del elemento "j" en comparación con la producida únicamente por la excitación electrónica. La contribución adicional de la fluorescencia por los rayos X característicos se denomina F (corrección de fluorescencia).

Los parámetros Z, A y F se utilizan normalmente para multiplicar el resultado obtenido por la "primera aproximación de Castaing". La llamada "corrección ZAF" es Z*A*F, y se aplica tanto a los estándares como a la muestra desconocida.

Si el material estándar tiene números ZAF idénticos a los números ZAF de la muestra desconocida, el efecto de la corrección matricial se anulará mutuamente (ZAF_i^unk = ZAF_i^std). Por esta razón, en la práctica, se intenta elegir estándares del mismo tipo de material que la muestra que analizamos como desconocida.

Lo que se hace es medir todos las razones k-ratios de todos los elementos que componen la muestra (excepto los estimados por estequiometría u otros métodos) y el sistema de ecuaciones resultante se resuelve mediante un procedimiento iterativo. Esto es necesario entre otras razones porque varias cantidades presentes en las ecuaciones que describen los factores de corrección dependen de las concentraciones desconocidas, que son las que se están calculando. En general, no obstante, la convergencia se logra rápidamente mediante procedimientos iterativos sencillos.

Por ejemplo, en un análisis de microsonda de un olivino (Mg_xFe_₁-x)₂SiO₄ que contiene O, Mg, Si y Fe, es necesario corregir los efectos del retardo y la dispersión de electrones (Z), la absorción de rayos X (A) y la fluorescencia de rayos X (F) de todos los elementos sobre todos los elementos. Se miden las intensidades de rayos X emitidos para las líneas Kα de Mg, Si y Fe en una muestra de olivino y en los estándares, calculándose las relaciones k para todos los elementos en relación con los estándares utilizados para cada elemento. Por ejemplo, la concentración de Mg en la muestra de olivino se obtiene multiplicando el coeficiente k de Mg por la concentración de Mg en el estándar de Mg, y todo se corrige multiplicando por los factores de corrección Z, A y F para el Mg en la muestra y en el estándar. La conversión de k a C se realiza mediante cálculo iterativo, inversión de matrices y otros tipos cálculo. En cualquier caso, se puede determinar la concentración desde el elemento traza hasta el elemento puro utilizando los algoritmos para los factores ZAF.

4b.- Análisis WDS y EDS mixtos y sin estándares.

Un detector de Espectrometría de Dispersión de Energía (EDS) colocado dentro de la cámara de muestra (sobre la muestra) de una EPMA puede identificar y discriminar los rayos X emitidos por su energía, así como puede contar los rayos X de diferente energía. El análisis EDS genera un espectro de intensidad de los rayos X característicos (número de cuentas por segundo) en función de su energía característica, generando picos en el espectro que se identifican y etiquetan automáticamente con el elemento y el tipo de línea de rayos X (FeKα, PbMβ, etc). Al igual que WDS, la altura del pico para el elemento "i" es proporcional a la concentración del elemento "i" en la muestra, por lo que al comparar la altura del pico con la de un estandard se puede calcular la concentración del elemento "i". La calidad de los análisis WDS y EDS es parecida, aunque la precisión de WDS es mayor.

Dado que el análisis EDS también puede hacerse con estándares, al igual que en WDS, comparando picos de la muestra desconocida con picos de los elemento medidos en el estándar, es posible realizar un análisis cuantitativo combinado donde algunos elementos se analizan en modo EDS y otros en modo WDS, siempre que la instrumentación tenga un detector EDS integrado en EPMA, o un espectrómetro de longitud de onda integrado en un SEM.

Así, aunque el análisis EPMA genérico basado en estándares aplica tanto para el EPMA/SEM WDS como para el EPMA/SEM EDS, muchos análisis se realizan sin que el usuario mida directamente los estándares, especialmente con EDS. Esto es, se puede comparar la altura del pico medido en la muestra con la de un "estándar virtual 100% puro". En el análisis sin estándares, se utilizan intensidades de elementos puros calculadas, derivadas de datos teóricos o empíricos contenidos en el software, en lugar de valores medidos. Esta opción se ofrece en la mayoría de los sistemas de dispersión de energía, pero su precisión es difícil de evaluar, aunque ciertamente no es tan buena como cuando se utilizan estándares reales.

La cuantificación sin estándares se basa en primeros principios, que permiten simular la generación, emisión y detección de rayos X. Las intensidades de los rayos X se calculan utilizando ecuaciones para una composición de muestra y condiciones analíticas dadas. Esto requiere el conocimiento no solo de magnitudes fundamentales, sino también de parámetros instrumentales. En cualquier caso, se puede calcular o extrapolar la intensidad de rayos X del elemento puro en unas condiciones analíticas dadas y crear un estándar virtual. Este método es muy susceptible a imprecisiones en los parámetros físicos y modelos, considerándose un análisis semi-cuantitativo. De hecho, a menos que la eficiencia del detector sea conocida y estable (es difícil de predecir la eficiencia de los espectrómetros), los estándares virtuales solo son aplicables de forma general a EDS. En los análisis sin estándares genera valores de la concentración de los elementos (% en peso) siendo la suma total de elementos lejana a 100%. Generalmente, el análisis se normaliza al 100%, pero su calidad debe evaluarse mediante inspeccionando la estequiometría resultante tras normalizar la composición a una fórmula estructural.

4c.- Comparación de EDS y WDS

Comparación práctica de EDS y WDS en términos de precisión de microanálisis cuantitativo mediante EDS y WDS en distintos laboratorios de un vidrio metálico a base de níquel. Participaron 56 laboratorios, con 69 columnas de electrones y 75 espectrómetros. El estudio se dividió en 56 microscopios electrónicos de barrido (SEM) y 13 sondas de electrones con confirguraciones variadas, 57 EDS (37 detectores SDD y 20 detectores de Si(Li)) y 18 sistemas WDS en 13 sondas de electrones y 5 SEM. Las condiciones descritas aquí corresponden a análisis bajo 15 o 20 kV.

El vidrio estaba compuesto de Ni (50,3 % en peso), Co (23,4 % en peso), Cr (10,4 % en peso), Mo (6,7 % en peso), Fe (5,6 % en peso) y B (3,6 % en peso).

El resultado clave de este estudio fue que, para cualquier laboratorio, existe una probabilidad significativa de un mayor error analítico con EDS que con WDS. La figura abajo muestra la dispersión de los resultados para Ni y Mo. La mayoría de los resultados de Ni con WDS se sitúan exactamente donde deberían (50-51 % en peso de Ni), en comparación con la mayoría de los resultados de EDS que se sitúan en un rango más amplio, entre el 51 % y el 53 % en peso. Hay tres veces más sistemas EDS representados que sistemas WDS, por lo que cabría esperar una mayor variación en los resultados de EDS, pero parece existir un problema de precisión. Los resultados de WDS y EDS para Mo coincidieron o se acercaron mucho a la composición objetivo, pero, una vez más, la variabilidad en los resultados de EDS fue mayor de lo deseable.

Histogramas de los resultados de medición de Ni y Mo en el vidrio mediante WDS y EDS en distintos laboratorios. A la izquierda, los resultados de EDS muestran un error de 1-2 % en peso, sobrestimando el contenido de Ni, en comparación con los resultados de WDS; además, los valores determinados por EDS se distribuyen en un rango más amplio. A la derecha, tanto EDS como WDS proporcionan valores de Mo correctos, aunque, nuevamente, hay suficientes mediciones de EDS fuera de un rango de error razonable (Jonnard et al., 2015).

Datos adicionales para la comparación EDS-WDS interlaboratorio se ofrecen en la figura de abajo. Los datos para EDS se descompone en SDD y Si(Li); para Ni, ambos dan generalmente resultados demasiado altos, con más dispersión para SDD en comparación con Si(Li). Mo también muestra un alto grado de dispersión. Por otro lado, los datos WDS de las sondas electrónicas son mucho menos dispersos y más próximos a la composición del material. La excepción son los detectores WDS montados en SEM: aquí la dispersión se aproxima o supera a la de EDS. Las diferencias instrumentales clave entre los SEM y las sondas electrónicas incluyen: (i) posiblemente menos estabilidad del haz, (ii) potenciales errores en el ángulo de despegue (deslizamientos del detector EDS hacia adentro o hacia afuera, lo que potencialmente cambia el ángulo de despegue) y (iii) sin un microscopio óptico en EDS para enfocar la superficie de la muestra, la distancia de trabajo puede variar.

Resultados de 66 sistemas EDS y 18 sistemas WDS en distintos laboratorios. La figura muestra datos de todos los elementos, así como desgloses por tipo de EDS y la separación de los WDS en sondas electrónicas en comparación con los WDS montados en microscopios electrónicos de barrido (SEM). Los valores del eje x representan números asignados arbitrariamente a los instrumentos. Ruste J. Circuit d’intercomparaison 2012-2013. Group Natl Microsc Electron à Alayage Microanal 2013.

5a.- Análisis cerca de los límites de fase y el problema de la fluorescencia secundaria

La región de la muestra desde la que se generan los rayos X primarios es de varias micras cúbicas, pero la región donde se produce fluorescencia secundaria puede ser de uno a dos órdenes de magnitud mayor. Esto significa que incluso con un haz de electrones que incide a una distancia considerable del límite con otra fase, puede haber rayos X emitidos desde la fase adyacente que alcancen el detector. Esta contribución, conocida como fluorescencia de límite o fluorescencia secundaria (FS) cerca de los límites de fase, puede ser una fuente de error significativa al analizar un elemento (particularmente traza/menor) en una fase próxima a otra que contenga el elemento de interés.

Por ejemplo, en la figura abajo se aprecia dos fases puras en contacto, Cu y Co metálicos y que no han sido sometidos a procesos de inter-difusión (o sea, Cu no contiene Co y Co no contiene Cu). Es claro que el incremento de la concentración de uno en otro a medida que la sonda se acerca al límite de fase es aparente. Más aún, el perfil aparente registrado se parece a perfiles de difusión elemental, lo que puede llevar a errores conceptuales importantes.

Este problema es agudo y difícil de resolver a la hora de analizar en inclusiones pequeñas dentro de otras fases minerales. Tanto en este caso como en otros relacionados con cercanía del límite de fase pueden llevarse a cabo modelos matemáticos de sustracción de una fase en la otra, si bien la calidad del análisis resultante calculado puede ser deficiente.

Ejemplo de fluorescencia secundaria que imita la difusión elemental. En este caso, los dos materiales puros se montan uno junto al otro, sin difusión. Los códigos PENEPMA y FANAL ("este estudio") simulan con precisión tanto la fluorescencia secundaria característica como la continua. De Llovet et al. (2012). Nótese que la distancia mínima para evitar la contaminación del análisis es de unas decenas de micras.

5b.- Ejemplo de rutina analítica

Este ejemplo es para una Jeol Superprobre

5c.- Criterios de exactitud (calidad)

Para evaluar la exactitud de los resultados de los análisis basados en estándares, tanto en res, tanto en WDS como EDS (utilizando explícitamente un material de referencia local para adquirir los recuentos de rayos X y generar la relación k requerida), se utiliza una prueba sencilla: ¿el porcentaje de masa (peso) analítico total se encuentra en un rango cercano al 100 % en peso (sin normalizar a 100)? Idealmente, un total analítico "perfecto" debería estar entre el 99 y el 100,5 % en peso (un valor más bajo, ya que podría haber elementos sin medir, como el hidrógeno en minerales hidratados, con OH^- o H₂O molecular, o elementos minoritarios/trazas), aunque en la práctica se considera aceptable un margen más amplio.

Existe un segundo criterio de control de calidad, aplicable a algunos materiales en los que se sabe que los elementos existen en una relación estequiométrica bien definida. Sin embargo, esto puede ser complicado cuando existe un rango de solución sólida.

Existe un tercer criterio de equilibrio de carga para un material con enlace covalente.

Hay que indicar que todos los criterios anteriores pueden superarse en el caso de problemas relacionados con la cercanía de límites de fase. Esto es, dos fases en contacto analizadas cerca del mismo darán señales aparente de tener disuelta la fase adyacente en cierta cantidad (pudiendo ser o no solución sólida), la suma elemental será cercana al 100% (si las dos fases no contienen hidrógeno y si han analizado todos los elementos significativos) y las cargas estarán balanceadas (si se analizan todos los aniones y cationes significativos en materiales iónicos y covalentes).

Puede haber un problema de control de calidad cuando los usuarios de EPMA "solo" miran los valores de porcentaje atómico normalizado. El problema es que, si el total analítico está lejos del 100 % en peso, eso es una señal de alerta inmediata de que hay problemas con el análisis, por ejemplo, un elemento no analizado en el desconocido (total bajo), un estándar dañado (total alto) o fluorescencia secundaria de fases adyacentes (total alto). Esta señal de alerta indica que no se puede asumir que los valores atómicos normalizados sean correctos. Por esa razón, el total de porcentaje en peso no normalizado siempre debe consultarse antes de aceptar los valores atómicos normalizados, y los informes siempre deben  incluir los totales analíticos (% en peso) sin normalizar.

Control de calidad.

5d.- Aplicaciones inadecuadas

En ocasiones, los usuarios de WDS o EDS intentan utilizar el instrumento y el proceso analítico de forma inadecuada. A continuación, se presentan tres ejemplos basados en experiencias reales de laboratorio:

1. “Solo me interesa un elemento de esta muestra, así que, por favor, no mida ningún otro”: El material obviamente contiene más de un elemento, por lo que la intensidad de rayos X medida para el elemento “objetivo” se ve modificada por la matriz. Por lo tanto, TODOS los elementos presentes en la muestra DEBEN medirse (o al menos tenerse en cuenta) para determinar la concentración correcta del elemento objetivo.ento objetivo.

2. Una variante de esto es la creencia de que se puede medir mediante WDS o EDS la composición de una película delgada sobre un sustrato “ignorando los elementos del sustrato y renormalizando los elementos de la película”. Nuevamente, esto puede generar errores, ya que el haz de electrones penetra la película y, por lo tanto, la "ve" en una fracción de la profundidad que recorren los electrones. Por lo tanto, esos rayos X no se generan de forma similar a como se generan dentro del material de referencia. Por lo tanto, las relaciones k de los elementos de la película son "incorrectas" incluso antes de que entren en la corrección de la matriz. A esto se suma la posibilidad de que los rayos X en el sustrato provoquen fluorescencia secundaria en la película, generando más errores. Existe una forma correcta de determinar la composición de películas delgadas mediante EDS y WDS.

3. Análisis de haz desenfocado: En ocasiones, se utiliza EPMA para intentar lograr un análisis de un área relativamente grande. El volumen de interacción de los haces de electrones incidentes de 15-20 kV es del orden de 1-2 µm, dependiendo de la composición y la densidad del objetivo. Sin embargo, a veces se solicita a un laboratorio la determinación de la composición química de una pequeña región heterogénea/multifásica dentro de una muestra. Dado que el haz de electrones en modo puntual puede desenfocarse o configurarse en modo de escaneo rectangular, se puede creer que estos modos de desenfocado/escaneo pueden recolectar rayos X de un área extensa (de hasta 50–100 µm de ancho), lo que produce una composición química promedio correcta. Sin embargo, esta aplicación de EPMA es propensa a errores, ya que viola un principio clave del procedimiento de corrección (rayos X → relación k → corrección matricial → resultado para cada volumen analítico discreto), que es que el volumen de interacción es homogéneo, de modo que se aplica una corrección única. Si el haz genera rayos X en más de una composición química, la corrección matricial promediará los factores de corrección, generando errores. Dado que en muchas situaciones la corrección por absorción puede ser la corrección más importante, el sobreescaneo en muchos casos genera totales sintomáticamente altos. El procedimiento adecuado es adquirir mapas de rayos X, cuantitaticarlos, y luego procesarlos para generar composiciones globales correctas áreas pequeñas o grandes.

5.e.- Directrices para la presentación de resultados de EPMA/SEM

Las publicaciones de investigación y reportes técnicos deben proporcionar una descripción de las técnicas utilizadas y los procedimientos analíticos seguidos para la obtención de los datos reportados (mediante EDS o WDS), incluyendo, a ser posible:

1. Instrumento utilizado (fabricante y modelo), voltaje de aceleración, corriente del haz (si se mide) y si el haz está enfocado o desenfocado (y su tamaño).

2. Para EDS: marca y modelo del detector de energía; tipo de ventana, ±(constante de tiempo, tiempo muerto, ángulo de despegue, software).

3. Para WDS: cristales específicos utilizados para la difracción de RX, especialmente para elementos ligeros, ±(valor de espaciado 2d; analizador de altura de pulso (PHA); ángulo de despegue; software).

4. Preparación de la muestra: nivel de pulido ±(conductividad eléctrica), material de recubrimiento ±(espesor).

5. Estándares para cada elemento medido.

6. Si se determinaron elementos por diferencia, estequiometría u otro método (e.g., H, O,..).

7. Tiempo de contaje (línea de rayos X y fondos), error analítico y límites de detección de trazas.

8. Qué corrección matricial se utilizó (es decir, qué ZAF específico o qué modelo se utilizó)

9. ±(Líneas de rayos X medidas/utilizadas, posiciones (energías) donde se midieron los valores de fondo (si se midieron), modelo utilizado para describir el fondo (lineal, exponencial, pendiente, multipunto, MAN).

10. ±(Si se utilizaron procedimientos específicos: anticontaminación; estrategia de conteo dependiente del tiempo; correcciones por interferencias).

11. ±(Si se trata de elementos ligeros, fuente de los MAC utilizados).

12. Directrices utilizadas para el control de calidad de los datos (p. ej., totales analíticos no normalizados, totales analíticos excluidos por debajo o por encima de un umbral de % en peso determinado, otros criterios).

13. Los totales analíticos no normalizados del % en peso deben proporcionarse como comprobación analítica, además de fórmulas estructurales.

14. Detalles experimentales de los mapas de RX (elementales). Condiciones, cuantificación en su caso, etc.

5f.- Ejemplos

Ejemplo tomado de García-Casco et al. (2025) A general conceptual petrological model for the subsolidus transformation of chromitite with application and implications. Journal of Petrology, 66(4), egaf029 > DATA in Interdisciplinary Earth Data Alliance (IEDA)

Back-scattered electron (BSE) images, quantitative electronprobe microanalyses and X-ray (XR) elemental maps were obtained with a JEOL JXA-8230 at the Centres Científics i Tecnològics, Barcelona University (CCiTUB), operated in wavelength-dispersive spectroscopy (WDS) mode. Operating conditions for point analyses were 20 kV acceleration potential, 15 nA beam current, focused beam and 20 seconds/element (see Pujol-Solà et al., 2021 for further details).

Spinel analyses were normalized to 4 oxygens and 3 cations, while the analyses of chlorite were normalized to 20 oxygens, 16(OH) and 20 cations (Supplementary Table S1 and EarthChem Library link). Fe³⁺ content was estimated by stoichiometry. Atoms per formula unit is abbreviated apfu.

X-ray maps were collected using the EPMA operated in WDS mode by stage scanning, with an accelerating voltage of 20 kV, beam current of 300 nA, dwell time of 20 ms per pixel, and pixel sizes (point spacing) of 0.38 to 2.5 μm. Experiments have demonstrated that short counting time (milliseconds rather than seconds) precludes beam damage at high beam current (García-Casco, 2007). The raw counts were transformed into oxide wt % with the ZAF correction. All maps were converted into molar oxide and atomic proportions and manipulated with DWImager software (see García-Casco, 2007; Torres-Roldán & Garcia-Casco, N.D.). This software was used to extract the bulk-compositions of the scanned areas and micro-domains.

Reactions and tetrahedral and triangular projections have been obtained using algebraic methods (matrix analysis; e.g. Spear et al., 1982) with CSpace (Torres-Roldan et al., 2000; see also Garcia-Casco et al., 2020) and Excel softwares. In the end-member system MgO–Al₂O₃–SiO₂–H₂O (MASH) (system components = 4), stoichiometric coefficients of reactions among 5 selected phases (e.g. forsterite, spinel, chlorite, brucite and H₂O fluid, eq. 6 below) are straightforwardly found by matrix analysis. Bulk rock compositions in the 6-component system FeO–MgO–Al₂O₃–Cr₂O₃–SiO₂–H₂O (FMACrSH) were algebraically mapped in new 6-dimensional coordinate systems defined by Mg–Al-bearing mineral end-members, exchange vectors Cr₂O₃(Al₂O₃)₋₁ and FeO(MgO)₋₁ (hereafter abbreviated FeMg₋₁ and CrAl₋₁, respectively) and H2O fluid, such as in eq. 11.

Whole-rock compositions developed upon metasomatic MgO-loss from, or SiO₂-addition in, model chromitite (0.8:0.2 spinel/olivine ratio, molar units, WR0 below) were calculated in the FMACrSH system iteratively until an assemblage made of spinel and chlorite is reached (e.g. eq. 18 below). Most calculations were performed in molar units, but some are offered in oxy-equivalent units (e.g. eq. 19 below) to approximate the volume proportions of the solid phases (Brady & Stout, 1980; Thompson, 1982; Garcia-Casco et al., 2020). These calculations were combined with calculations involving Fe–Mg and Al–Cr exchanges between olivine and spinel and chlorite and spinel using varied distribution coefficients (K_Ds), as justified below.

Triangular and tetrahedral phase diagrams for the 6-component FMACrSH system involve projection from phases and exchange vectors, as indicated in the corresponding figures. Thermodynamic calculations have been performed using GeoPS v3.5.4 (Xiang & Connolly, 2022) and the thermodynamic dataset HP633 (Holland & Powell, 2011) and associated solutions models for olivine, orthopyroxene, spinel and garnet (Holland et al., 2018), plus chlorite, chloritoid, staurolite, cordierite (White et al., 2014) and talc (ideal Fe–Mg solution) and H₂O-fluid (Holland & Powell, 1998). Mineral abbreviations are after Warr (2021).

Ejemplo tomado de Domínguez-Carretero et al 2024. The Geology, Geochemistry, and Mineralogy of the Moa Bay Ni Laterite Mining District, Cuba. Economic Geology 119 (7), 685-1706.

Electron microprobe analyses on oxyhydroxides (goethite, maghemite, Mn oxyhydroxides) and silicates (serpentine and garnierite) were conducted at CCiT-UB with a JEOL JXA-8230 equipment with four wavelength-dispersive spectrometers (WDS) and one EDS system (App. 5). The analytical conditions were 15- to 20-kV accelerating voltage, 10- to 20-nA beam current, 1- to 2-μm beam diameter, and 10- to 20-s counting time (peak and background) per element. Measurements and calibrations were performed using the following natural and synthetic standards: hematite (Fe), rutile (Ti), periclase (Mg), rhodonite (Mn), Al₂O₃ (Al), Cr₂O₃ (Cr), diopside (Si), NiO (Ni), wollastonite (Ca), orthoclase (K), metallic cobalt (Co), and sphalerite (Zn).

A special EMP procedure was designed for measuring Sc in goethite, maghemite, Mn oxyhydroxides, and hematite from the Punta Gorda and Yamanigüey deposits. Scandium was measured first with four WDS instruments and one EDS instrument for 12 min of counting time (peak and background), followed by the analysis of Si, Al, Cr, Mg, Ti, Co, Ni, Fe, and Mn with counting times of 10 to 20 s (peak and background), for a 20-kV accelerating voltage and 15-nA beam current with a probe size of 5 μm. The standards used were the same as for the procedure used for major elements in oxyhydroxides and silicates, plus metallic scandium to calibrate Sc. The detection limit for Sc for these analyses is 15 ppm. Maghemite and hematite Sc measurements were all below the limit of detection.

The structural formulae of serpentine group minerals were calculated on the basis of 7 oxygens and that of garnierites on the basis of 7 or 11 oxygens, depending on the predominance of serpentine or kerolite-pimelite (talc) in the mixture. The talc fraction or X_talc in the mixture was calculated using the method of Villanova-de-Benavent et al. (2022). Iron in primary hydrothermal serpentine (“serpentine I”) was calculated as Fe²⁺, and in secondary weathering serpentine (“serpentine II”) and in garnierites as Fe³⁺ (Roqué-Rosell et al., 2017; Villanova-de-Benavent et al., 2017).

Ejemplo tomado de Pujol-Solà et. al. (2021). The chromitites of the Neoproterozoic Bou Azzer ophiolite (Central Anti-Atlas, Morocco) revisited. Ore Geology Reviews 134, 104166.

We studied representative samples from three chromitite mining sites in the Bou Azzer ophiolite: Inguijem, Filon 60 and Ait Ahmane (Fig. 1, Fig. 2), including massive chromitites from individual pods (n = 4), semi-massive chromitites (n = 2), banded chromitites (n = 1) and the host dunites. Polished thin sections were studied by optical and electron microscopy using a Quanta 200 FEI XTE 325/D8395 scanning electron microscope (SEM) equipped with an INCA Energy 250 EDS microanalysis system and a JEOL JSM-7100 field-emission SEM at the Centres Científics i Tecnològics de la Universitat de Barcelona (CCiTUB). Operating conditions were 20 kV accelerating voltage. Micro-Raman spectra were obtained with a HORIBA JobinYvon LabRam HR 800 dispersive spectrometer equipped with an Olympus BXFM optical microscope at the CCiTUB. Non polarized Raman spectra were obtained in confocal geometry by applying a 532 nm laser, using a 100x objective (beam size around 2 µm), with 3–5 measurement repetitions for 10–15 s each. The Si band at ~520 cm⁻¹ was used for calibration. The obtained spectra were processed using the LabSpec® software (JobinYvon; Villeneuve-d’Ascq, France).

Quantitative electron microprobe analyses (EMPA) on chromite and platinum group minerals (PGM) were also conducted at the CCiTUB using a JEOL JXA-8230 operating in wavelength-dispersive spectroscopy (WDS) mode. Analytical conditions are described in detail in Appendix 1. X-ray (XR) images of chromite (512 × 512 pixels, 0.52 × 0.52 µm pixel size and 266.24 × 266.24 µm total area) and platinum group minerals (three images of 300 × 300 pixels: 0.22 µm pixel size and 66 × 66 µm total area, 0.08 µm pixel size and 24 × 24 µm total area and 0.1 µm pixel size and 30 × 30 µm total area) were obtained with the same a JEOL JXA-8230 electron microprobe operated at 20 kV and 20nA in spot mode with focused electron beam and counting time of 20 to 60 ms/pixel. The images were treated with DWImager software (Torres-Roldán & Garcia Casco, unpublished; see Garcia-Casco, 2007). Minor and trace elements in chromite were analyzed using a Resolution M-50 Excimer laser coupled to a ThermoICap Qc inductively coupled mass spectrometer at the Laboratorio de Estudios Isotópicos (LEI) from the Centro de Geociencias, UNAM (Mexico). The analytical conditions and procedure are described in Appendix 1.

Appendix 1. Electron microprobe analyses (EMPA)

Quantitative analyses of chromite and platinum group minerals (PGM) were performed using a five-channel JEOL JXA-8230 electron microprobe at the Centres Científics i Tecnològics de la Universitat de Barcelona (CCiTUB). The analytical conditions were 15 - 20 kV accelerating voltage, 10 - 20 nA beam current, 1 - 2 µm beam diameter, and 10 - 20 s counting time per element, using WDS detectors and XPP matrix correction (Pouchou and Pichoir, 1990). The results for chromite were stoichiometrically recalculated to distinguish FeO and Fe₂O₃ according to the procedure described by Carmichael (1967). The measurements and the calibrations for chromite and PGM analyses were performed using natural and synthetic standards and are shown in Tables A and B.

Microscopía electrónica > Cuantificacion

[Intro] [Interacciones e-muestra] [EPMA] [SEM] [Fuentes de emisión] [El haz] [Muestras] [SE] [BSE] [CL] [EBSD] [RX] [Ley de Bragg] [WDS] [EDS] [Mapas de RX] [Detectores] [Cuantificación de la señal] [Datación monacita] [Manual de procedimientos]

Última modificación: domingo, 16 de noviembre de 2025 17:43 +0100