Práctica 1. Ecuaciones Diferenciales Ordinarias.
Veremos en esta práctica cómo resolver simbólicamente ecuaciones diferenciales usando Wolfram|Alpha y cómo obtener soluciones numéricas mediante el método de Euler.
Contents
- Solución simbólica de una ecuación diferencial
- Solución general de una ecuación diferencial
- Solución particular de un PVI
- Circuito RLC
- Solución numérica un PVI. Método de Euler.
- Tabla de resultados
- Gráfica de la poligonal
- Comparación con los valores exactos
- Tabla de errores
- Gráfica
- Ejercicios finales
Solución simbólica de una ecuación diferencial
Para calcular una solución exacta (analítica) de una ecuación diferencial basta escribirla adecuadamente en la página de Wolfram|Alpha
Solución general de una ecuación diferencial
Para este ejemplo abrimos la página www.wolframalpha.com y escribimos DSolve[ y'(x)-2*x*y(x)=0 ] En los resultados puede ver la clasificación de la ecuación, la solución general en términos de una constante c_1, el campo de pendientes e incluso una muestra de la familia de soluciones en términos del valor de y(0).
Observe que hemos escrito la función incógnita con su variable y(x) . Wolfram|Alpha es flexible con la notación que usamos, a cambio debemos prestar atención a cómo ha interpretado nuestra petición y, en ocasiones, nos puede pedir información adicional.
Ej 1 . Halle la solución general de x*y'(x)-y^2+9=0 . (solución : y(x) = -(3 (e^(6 c_1) x^6 - 1))/(e^(6 c_1) x^6 + 1) )
Solución particular de un PVI
De forma similar, incluyendo las condiciones iniciales, se obtiene la solución particular de una problema de valores iniciales. Introduzca la instrucción DSolve[ y'(x)-2*x*y(x)==0, y(0)==2 ]
Vemos que en este caso la solución no incluye la constante c_1 y obtenemos la gráfica de y(x) .
Ej 2. Halle la solución de x*y'(x)-y^2+9=0 que cumple que y(1)=7 . (solución : y(x) = (6 x^6 + 15)/(5 - 2 x^6) ).
Circuito RLC
También es posible resolver ecuaciones de orden superior. Escriba la instrucción DSolve [ 0.2*i''(t)+330*i'(t)+(1/(20*10^-6))*i(t)=0, i(0)=0, i'(0)=30 ] donde la función i(t) es la corriente, variable del problema, no es la unidad de los números complejos. La ecuación está tomada de https://youtu.be/w9Z4Ly98Lcw?t=143 donde se resuelve el problema paso a paso.
Solución numérica un PVI. Método de Euler.
Nos planteamos aplicar el método de Euler al siguiente problema de valor inicial y'(x)=f(x,y) para x en el intervalo (x0,xn), y(x0)=y0 .
Comenzamos definiendo dos variables para la condición inicial primero x0 y a continuación y0 .
x0=0.0 y0=3.0
x0 =
0
y0 =
3
Para implementar el método de Euler aproximamos el valor de la solución en unos puntos x0, x1, ..., xn también llamados nodos. Definimos ahora el valor de último punto xn, el número de intervalos que definen los puntos n y la distancia entre los puntos h.
xn = 1 n = 10 h = (xn - x0)/n
xn =
1
n =
10
h =
0.1000
Ahora necesitamos definir la función f. Veremos más adelante cómo definir funciones en un script, pero ahora lo haremos mediante una función anónima con la siguiente sintaxis con lo que tendremos f(x,y)=2*x*y .
f=@(x,y) 2*x*y
f =
@(x,y)2*x*y
Definimos los puntos x1, x2, ..., xn en un vector, indicando el primer punto, x0, luego la longitud de los intervalos o paso, h, y luego el último punto. Inicializamos Y como un vector de ceros (una fila, n+1 columnas).
X=[x0 : h : xn] Y=zeros(1,n+1)
X =
Columns 1 through 6
0 0.1000 0.2000 0.3000 0.4000 0.5000
Columns 7 through 11
0.6000 0.7000 0.8000 0.9000 1.0000
Y =
0 0 0 0 0 0 0 0 0 0 0
Ahora definimos los valores de los puntos yi . Como ilustración hemos sacado la definición de Y(2) fuera del bucle.
Y(1)=y0; Y(2)=Y(1) + f(X(1), Y(1)) * (X(2) - X(1)); for i= 3:n+1 Y(i)=Y(i-1) + f(X(i-1), Y(i-1)) * (X(i) - X(i-1)); end
Tabla de resultados
Para ver los valores hallados, trasponemos el vector con los puntos de X para que quede como una columna, hacemos lo mismo con Y y mostramos los dos vectores uno junto a otro.
[X' , Y']
ans =
0 3.0000
0.1000 3.0000
0.2000 3.0600
0.3000 3.1824
0.4000 3.3733
0.5000 3.6432
0.6000 4.0075
0.7000 4.4884
0.8000 5.1168
0.9000 5.9355
1.0000 7.0039
Gráfica de la poligonal
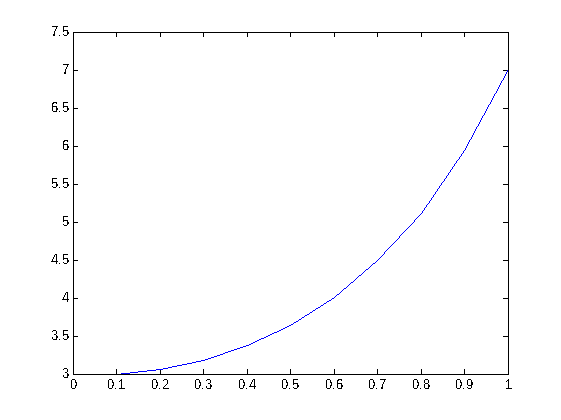
Podemos ver la gráfica de la poligonal formada por los puntos (xi, yi) . (El código del método está en el script MetEuler.m )
plot(X,Y)
Comparación con los valores exactos
En este caso podemos comparar los resultados obtenidos por el método numérico con los valores exactos porque podemos definir la función exacta (analítica) y evaluarla en los puntos del vector X, para lo cual hemos puesto un punto antes del signo de elevado al definir la función
yexacta=@(x) 3*exp(x.^2) Ye=yexacta(X)
yexacta =
@(x)3*exp(x.^2)
Ye =
Columns 1 through 6
3.0000 3.0302 3.1224 3.2825 3.5205 3.8521
Columns 7 through 11
4.3000 4.8969 5.6894 6.7437 8.1548
Tabla de errores
Para ver mejor los resultados los mostramos en columnas. La primera columna son los puntos x0, x1, ..., xn. En la segunda columna se ven los valores hallados por el método de Euler. En la tercera columna están los valores exactos y en la cuarta la diferencia entre los valores exactos y los aproximados, con lo que podemos ver los errores que se cometen.
[X', Y', Ye', (Ye-Y)']
ans =
0 3.0000 3.0000 0
0.1000 3.0000 3.0302 0.0302
0.2000 3.0600 3.1224 0.0624
0.3000 3.1824 3.2825 0.1001
0.4000 3.3733 3.5205 0.1472
0.5000 3.6432 3.8521 0.2089
0.6000 4.0075 4.3000 0.2925
0.7000 4.4884 4.8969 0.4085
0.8000 5.1168 5.6894 0.5726
0.9000 5.9355 6.7437 0.8082
1.0000 7.0039 8.1548 1.1509
Vemos que en los primeros nodos los errores son relativamente pequeños 0.0302, 0.0624,... pero que van creciendo conforme nos alejamos de la condición inicial
Gráfica
Para comparar gráficamente los resultados con la solución exacta del problema, definimos un vector XE con más puntos, definimos una función yexacta con la solución exacta del problema 3*e^(x^2), y evaluamos la función en todos los puntos de XE, para lo cual hemos puesto un punto antes del signo de elevado al definir la función.
XE=[x0:h/4:xn]; YE=yexacta(XE); plot(X,Y,XE,YE)
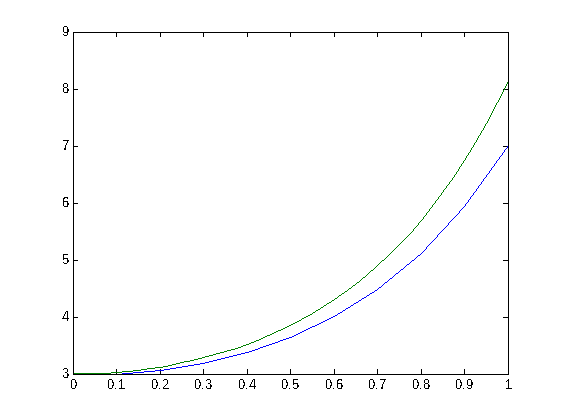
Ej 3. En la gráfica se representan dos funciones ¿cuál es la exacta y cuál la aproximada? (Indicación: mire la tabla de errores.)
Ejercicios finales
Ej 4. Se quiere emplear el método de Euler con h = 0.05 para hallar una solución aproximada de y(2) en la misma ecuación diferencial del ejemplo anterior (y'(x)=f(x,y)=x+y, y(0)=3).
a) Halle el número n de partes en las que se debe dividir el intervalo [0, 2] y obtenga dicha solución aproximada.
b) Use el mismo paso h=0.05 para hallar una aproximación a y(3).
Ej 5. Se considera el problema de valor inicial y'(x) = 3y^2 -x^2, y(0)=0.15
a) Halle una aproximación de y(3) usando h=0.1.
b) Halle una aproximación de y(3) usando h=0.05.
c) Suponiendo que y(3) vale -1.673381304457, ¿cuál de los dos valores de h permite obtener la mejor aproximación de y(3)? (solución : Exacto - aproximado=0.0001, Exacto - aproximado=5.418e-05, más pequeño )
Ej 6. Dentro del bucle del método de Euler, ¿se puede sustituir (X(i) - X(i-1)) por h? Justifique la respuesta.
Ej 7. Halle una aproximación de la solución de y'(x)=2y-(3/10)y^2, y(0)=1/10 en x=4 usando el método de Euler en el intervalo (0,4) para n=25. Represente la poligonal del Euler.
Sabiendo que la solución exacta es y(x)= (20 e^(2x)) / (197 + 3e^(2x)) ¿Qué error absoluto se está cometiendo? (Valor exacto menos valor aproximado). (Sol. y(4)=~ 6.5164. Error=0.00653 .)
% Ecuaciones Diferenciales y Cálculo Numérico. (A. Palomares) % Grado en Ingeniería de Tecnologías de Telecomunicación. disp(date)
01-Mar-2023