Práctica 4. Límites. Continuidad.
En esta práctica veremos como hallar límites de funciones reales de variable real, y los
usaremos para estudiar la continuidad de una función en un punto.
1 Límites
1.1 El comando limit.
Para hallar límites con Maxima se emplea el comando limit. La sintaxis general del comando es
limit( expresión, variable, punto, dirección ). En los siguientes apartados veremos como usar
el comando para hallar límites en un punto, límites laterales y límites en infinito.
1.2 Límite en un punto.
Para hallar el límite de una función en un punto, basta indicar la función, la variable y el
punto.
| (%i1) | limit(sin(x)/x,x,0); |
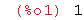
Ejercicio. Halle el límite de la función sen(2x)/x cuando x tiende a 0.
(Sol. 2 ).
Al hallar un límite, Maxima devuelve el resultado 'und' cuando el resultado es indefinido
(undefined), y el resultado 'ind' cuando el resultado es indeterminado pero acotado
(indefinite). Veamos un ejemplo de cada caso.
En primer lugar buscamos el límite cuando x tiende a cero de sen(1/x) .
| (%i2) | limit( sin(1/x), x, 0); |

| (%i3) | wxplot2d(sin(1/x),[x,-1,1]); |
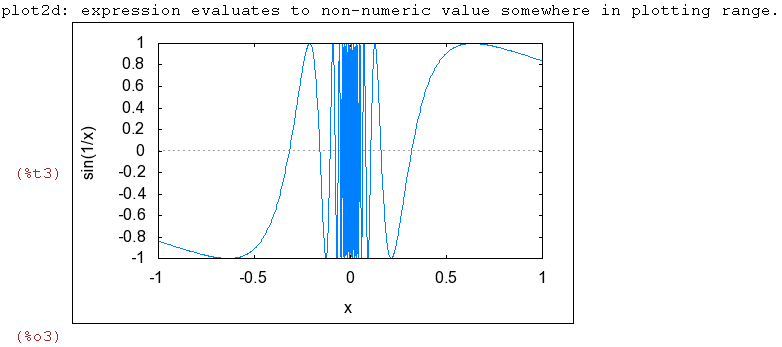
En este caso, cuando x tiende a cero, 1/x tiende a infinito y el seno de 1/x no tiende a un
número sino que oscila entre -1 y 1, con lo que sen(1/x) no tiene límite, pero está acotado.
A continuación buscamos el límite cuando x tiende a cero de la función
f(x)=(1/x)*sin(1/x).
| (%i4) | limit((1/x)*sin(1/x),x,0); |
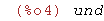
| (%i5) | wxplot2d((1/x)*sin(1/x),[x,-1,1],[y,-100,100]); |
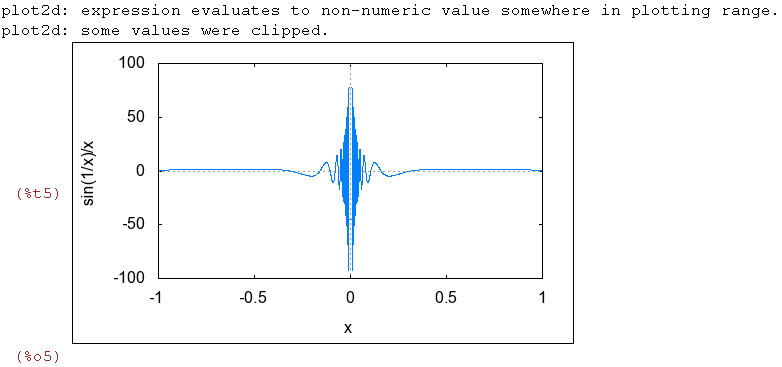
En este caso, al acercarnos a cero, estamos multiplicando la función (1/x) que no está acotada,
por la función sin(1/x) que oscila entre -1 y 1, con lo que la al acercarnos a cero la función
oscila cada vez con mayor amplitud.
1.3 Límites laterales.
Si queremos hallar el límite de la función 2^(1/x) cuando x tiende a 0, Maxima nos devuelve que
es indefinido.
| (%i6) | limit(2^(1/x),x,0); |
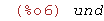
Hallaremos los límites laterales para obtener información más precisa. Para esto, debemos
indicar en el comando limit por qué lado queremos calcular el límite. Si ponemos 'minus'
calculará el límite por la izquierda, si ponemos 'plus' calculará el límite por la derecha.
| (%i7) | limit(2^(1/x),x,0,minus); |
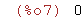
| (%i8) | limit(2^(1/x),x,0,plus); |
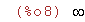
Así, vemos que se obtiene 0 si x tiende a 0-, (límite cuando x tiende a cero por la izquierda,
es decir límite cuando x tiene a cero mediante x<0), y se obtiene infinito si x tiende a 0+,
(límite cuando x tiende a cero por la derecha, es decir límite cuando x tiende a cero mediante
x>0).
En el siguiente ejemplo Maxima devuelve infinity, que significa que en módulo (en valor
absoluto) la función tiende a infinito.
| (%i9) | limit(tan(x),x,%pi/2); |
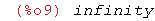
De nuevo, para concretar más, hallamos los límites laterales.
| (%i10) | limit(tan(x),x,%pi/2,minus); |

| (%i11) | limit(tan(x),x,%pi/2,plus); |
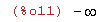
Vemos que el límite por la izquierda es mas infinito, y por la derecha es menos infinito.
Ejercicio. Halle el límite de la función f(x)=(x^3-1)/(x^2-1) cuando x tiende a -1.
(Sol. No existe límite. Por la izquierda es menos infinito, por la derecha es mas infinito)
Ej. Halle los límites laterales en 1 de 3^(1/(x-1)) .
(Sol. Por la izquierda 0, por la derecha infinito )
*Ejercicio. Considere la función f(x)=arccos(x-1).
Halle el límite cuando x tiende a 0 por la derecha de la función f.
¿Puede hallarse el límite cuando x tiende a cero por la izquierda?
¿Existe el límite de f cuando x tiende a cero?
(Indicación: Halle f(-0.00001). Represente f en el intervalo [-1,1]. )
1.4 Límites en infinito.
Para hallar límites en infinito introducimos inf en lugar del punto.
Para hallar límites en menos infinito introducimos minf en lugar del punto.
| (%i12) | wxplot2d(atan(x),[x,-100,100]); |
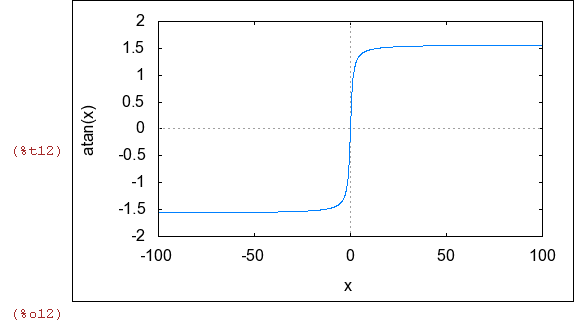
| (%i13) | limit(atan(x),x,inf); |

| (%i14) | limit(atan(x),x,minf); |

Ej. Halle el límite cuando x tiende a infinito de la función (1+1/x)^x .
(Sol. e ).
Ej. Halle el límite cuando x tiende a infinito de la función seno.
(Sol. ind, no existe. )
1.5 Límite de funciones a trozos.
El comando limit no sirve para hallar funciones a trozos definidas con if-then-else. Para
hallar límites de funciones a trozos, debemos nosotros elegir el 'trozo' de función adecuada
para hacer el límite.
| (%i15) | f(x):=if x<=0 then sin(2*x) else 2*x; |
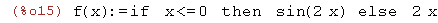
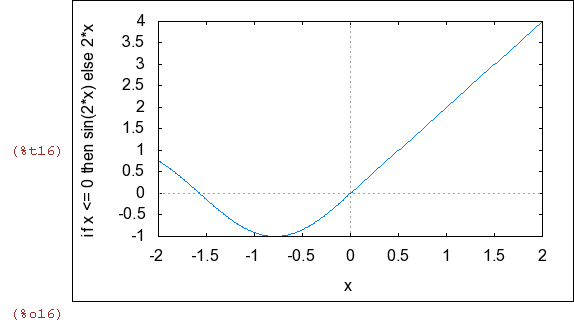
| (%i16) | wxplot2d(f(x),[x,-2,2]); |
| (%i17) | limit(f(x),x,0,minus); |
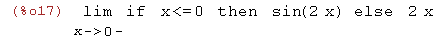
Si queremos hacer el límite de esta función cuando x tiende a cero por la izquierda, debemos
usar la función sin(2*x) .
| (%i18) | limit(sin(2*x),x,0,minus); |
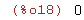
Para hallar el límite por la derecha usamos la función 2x .
| (%i19) | limit(2*x,x,0,plus); |
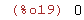
Observe que para hallar estos límites no es necesario definir la función con if-then-else .
Ejercicio. Considere la función f dada por f(x)=
x/(2^(1/x)+1) si x<0,
37 si x=0,
1/(2^(1/x)+1) si x>0.
Halle el límite cuando x tiende a 0 de la función f.
(Sol. 0)
2 Continuidad
Como hemos visto en teoría, una función es continua en un punto si (y solamente si) existe
el limite de la función en ese punto y vale igual que la función en ese punto.
Como ejemplo estudiamos la continuidad en cero de la función dada por f(x)=
x*sin(1/x) si x distinto de cero,
0 si x=0.
| (%i20) | limit( x*sin(1/x), x, 0, minus); |
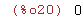
| (%i21) | limit( x*sin(1/x), x, 0, plus); |
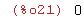
Como f(0)=0 y los límites laterales valen también 0, decimos que f es continua en cero.
Ejercicio.
Sea f(x)=
x si x<1,
x^2 si x>=1.
Compruebe si la función f es continua en x=1.
(Sol. Es continua).
Ahora vamos a considerar la siguiente función definida con un parámetro, f(x)=
a-x si x<1,
x^2-a si x>=1.
Queremos determinar si algún valor del parámetro a hace que la función sea continua.
En primer lugar borramos todas las variables y funciones, y definimos los dos trozos que
definen la función.
| (%i22) | kill(all); |
| (%i1) | f1(x):=a-x; |
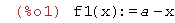
| (%i2) | f2(x):=x^2-a; |
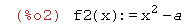
A continuación vamos a hallar el límite de la función cuando x tiende a 1, para lo cual usamos
límites laterales y las funciones definidas para cada trozo.
| (%i3) | limit(f1(x),x,1,minus); |
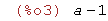
| (%i4) | limit(f2(x),x,1,plus); |
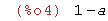
| (%i5) | f2(1); |
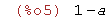
Para que los límites laterales coincidan con el valor de la función, debe ocurrir que a-1=1-a .
| (%i6) | solve(a-1=1-a,a); |

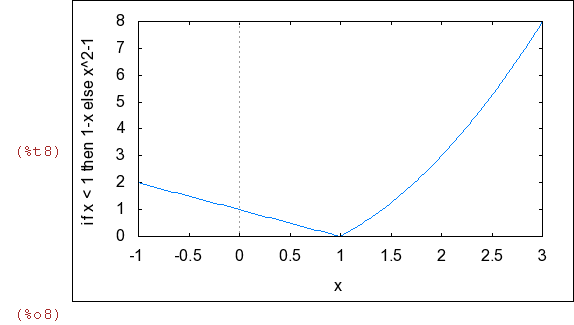
Así, si a=1, la función será continua. Vamos a representar la función para ese valor del
parámetro.
| (%i7) | f(x):=if x<1 then 1-x else x^2-1; |
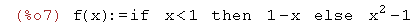
| (%i8) | wxplot2d(f(x),[x,-1,3]); |
Ejercicio. Calcule el valor de b para que la siguiente función sea continua.
g(x)=x+1 si x<0,
g(x)=b*e^x si x>=0.
(Sol. b=1 ).
3 Ejercicios
Ej. Defina la función f(x)=(x+1)/(x-1), y calcule el límite cuando x tiende a 2, los límites
laterales cuando x tiende a 1, y los límites cuando x tiene a infinito y a menos infinito.
(Sol. 3, menos infinito, mas infinito, 1, 1)
Ej. Halle el límite cuando x tiende a cero de la función x/abs(x) .
(Sol. No existe. Por la izquierda vale -1, por la derecha vale 1.)
Ej. Considere la siguiente función definida para x distinto de cero
f(x)=x/(3^(1/x)+1) .
¿Qué valor habría que darle a f(0) para que f fuese continua?
(Sol. 0)
Ej. Compruebe si es continua la siguiente función, f(x)=-1 si x<=2, f(x)=-x^2-4x-3 si x>2.
(Sol. No es continua.)
Ej. Calcule el valor de A para que sea continua la función
f(x)=e^(-x) si x < -2,
f(x)=x^2+2x+A si x>=-2.
(Sol. A=e^2 ).
Matemáticas II. Grado en Edificación. (A. Palomares.)